
L'inégalité (mathématiques)
À propos de ce écoles sélection Wikipedia
SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . enfants SOS est le plus grand don de charité du monde enfants orphelins et abandonnés la chance de la vie familiale.
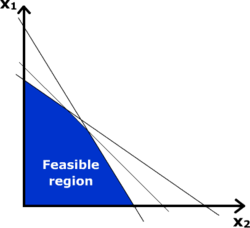
En mathématiques , une inégalité est une déclaration au sujet de la taille relative ou cet ordre de deux objets. (Voir aussi: l'égalité)
- La notation
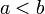 un moyen qui est inférieur à b, et
un moyen qui est inférieur à b, et - La notation
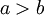 signifie que a est supérieur à b.
signifie que a est supérieur à b.
Ces relations sont connus comme inégalité stricte; en revanche
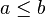 signifie que a est inférieur ou égal à b;
signifie que a est inférieur ou égal à b; 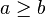 signifie que a est supérieur ou égal à b;
signifie que a est supérieur ou égal à b; 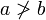 signifie que a ne est pas plus grand que b et
signifie que a ne est pas plus grand que b et 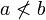 signifie que a ne est pas inférieur à b.
signifie que a ne est pas inférieur à b.
Une utilisation supplémentaire de la notation est de montrer que l'on est beaucoup plus grande quantité que l'autre, habituellement par plusieurs ordres de grandeur.
- La notation
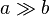 signifie que A est beaucoup plus grand que b.
signifie que A est beaucoup plus grand que b. - La notation
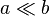 signifie que A est beaucoup inférieur à b.
signifie que A est beaucoup inférieur à b.
Si le sens de l'inégalité est la même pour toutes les valeurs des variables pour lesquelles ses membres sont définis, puis l'inégalité est appelée une inégalité «absolue» ou «inconditionnel». Si le sens d'une inégalité ne vaut que pour certaines valeurs des variables impliquées, mais est renversée ou détruit d'autres valeurs des variables, il est appelé une inégalité conditionnelle. Le sens d'une inégalité ne est pas modifié si les deux côtés sont augmentés ou diminués par le même nombre, ou si les deux côtés sont multipliés ou divisés par un nombre positif; le sens d'une inégalité est inversé si les deux membres sont multipliés ou divisés par un nombre négatif .
Propriétés
Les inégalités sont régies par les suivantes propriétés . Notez que, pour la transitivité, inversion, addition et la soustraction, multiplication et division et propriétés, la propriété est également titulaire si des signes d'inégalité stricte (<et>) sont remplacés par leur signe correspondant non stricte inégalité (≤ et ≥).
Trichromie
Le Etats propriété Trichotomy:
- Pour toute nombres réels , a et b, exactement une des conditions suivantes est remplie:
- <b
- a = b
- a> b
Transitivité
Le transitivité des inégalités déclare:
- Pour toute nombres réels , a, b, c:
- Si a> b et b> c; puis a> c
- Si a <b et b <c; alors un <c
Renversement
Les relations d'inégalité sont relations inverses:
- Pour toute nombres réels , a et b:
- Si a> b puis b <a
- Si un <b puis b> un
Addition et soustraction
Les propriétés qui traitent de plus et la soustraction Etat:
- Pour toute nombres réels , a, b, c:
- Si a> b, alors a + c> b + c et un - c> b - c
- Si a <b, alors a + c <b + c et un - c <b - c
ce est à dire, les chiffres réels sont un groupe ordonné.
Multiplication et division
Les propriétés qui traitent de la multiplication et de la division Etat:
- Pour toute nombres réels, a, b, c:
- Si c est positif et un <b, puis ac <bc
- Si c est négative et un <b, puis ac> bc
Plus généralement cela se applique pour un corps ordonné, voir ci-dessous.
Opposé
Les propriétés de la additif état inverse:
- Pour toute nombres réels a et b
- Si un <b puis - a> - b
- Si a> b alors - un <- b
Inverse multiplicatif
Les propriétés de la multiplicatif état inverse:
- Pour tout nombre réel a et b qui sont à la fois positifs ou les deux négatif
- Si un <b puis 1 / a> 1 / b
- Si a> b puis 1 / a <1 / b
L'application d'une fonction à deux côtés
Nous considérons deux cas de fonctions: monotone et strictement monotone.
Toute strictement monotone croissante fonction peut être appliquée aux deux côtés de l'inégalité et il va encore tenir. L'application d'une fonction strictement monotone décroissante de part et d'autre d'une inégalité signifie l'inégalité inverse est maintenant. Les règles d'additif et inverses multiplicatifs sont deux exemples de l'application d'une fonction décroissante monotone.
Si vous avez une inégalité non stricte (a ≤ b, a ≥ b) puis:
- Appliquer une fonction croissante monotone préserve la relation (≤ reste ≤, ≥ reste ≥)
- L'application d'une fonction décroissante monotone inverse la relation (≤ devient ≥, ≤ ≥ devient)
Il ne deviendra jamais strictement inégale, puisque, par exemple, 3 ≤ 3 ne implique pas que 3 <3.
Champs commandés
Si F, +, * être un ≤ champ et un ordre total sur F, alors F, +, *, ≤ est appelé champ si et seulement si commandé:
- si un ≤ b alors a + c ≤ b + c
- si 0 ≤ a et 0 ≤ b ≤ 0 alors ab
On notera que les deux 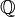 , +, *, Et ≤
, +, *, Et ≤ 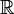 , +, *, Sont ≤ champs commandés.
, +, *, Sont ≤ champs commandés.
≤ ne peut être définie afin de rendre 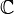 , +, *, Un ≤ corps ordonné.
, +, *, Un ≤ corps ordonné.
Les inégalités non strictes ≤ et ≥ sur nombres réels sont commandes totales. Les inégalités strictes <et> sur nombres réels sont Module: Total_order ( parler · · hist · · liens · sous-pages essais - résultats).
Notation Enchaîné
La notation <b <c signifie "a <b et b <c", à partir de laquelle, par la propriété de transitivité ci-dessus, il se ensuit également que <c. De toute évidence, par les lois ci-dessus, on peut ajouter / soustraire le même nombre à tous les trois termes, ou multiplier / diviser les trois termes par même nombre différent de zéro et inverser les inégalités selon le signer. . Mais il faut prendre soin de sorte que vous utilisez vraiment le même nombre dans tous les cas, par exemple, une <b + e <c est équivalent à un - e <b <c - e.
Cette notation peut être généralisé à tout nombre de termes: par exemple, un 1 ≤ 2 ≤ ... ≤ a n signifie qu'un i ≤ a i 1 pour i = 1, 2, ..., n - 1. Par transitivité, cette condition est équivalent à un i ≤ a j pour tout 1 ≤ i ≤ j ≤ n.
Lors de la résolution des inégalités en utilisant la notation en chaîne, il est possible et parfois nécessaire d'évaluer les termes indépendamment. Par exemple, pour résoudre l'inégalité 4 x <2 x + 1 ≤ 3 x + 2, vous ne serez pas en mesure d'isoler x une quelconque partie de l'inégalité par l'addition ou la soustraction. Au lieu de cela, vous pouvez résoudre 4 x <2 x + 1 et 2 + 1 x ≤ 3 x + 2 indépendamment, ce qui donne x <1/2 et x ≥ -1 respectivement, qui peuvent être combinés dans la solution finale -1 ≤ x < 2.1.
Parfois, la notation enchaîné est utilisé avec les inégalités dans des directions différentes, auquel cas le sens est le conjonction logique des inégalités entre les termes adjacents. Par exemple, un <b> c ≤ d signifie que <b, b> c et c ≤ d. En plus de l'utilisation rare dans les mathématiques, cette notation existe dans quelques langages de programmation tels que Python .
Représenter les inégalités sur la ligne de nombre réel
Chaque inégalités (sauf ceux qui impliquent nombres imaginaires) peuvent être représentés sur le réel numéro de ligne montrant des régions sombres sur la ligne.
Les inégalités entre les moyens
Il existe de nombreuses inégalités entre les moyens. Par exemple, pour des nombres positifs 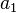 ,
, 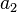 , ...,
, ..., 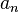
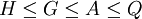 Où
Où
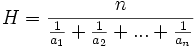 ( moyenne harmonique),
( moyenne harmonique),
![G = \ sqrt [n] {a_1 \ cdot a_2 \ cdot ... \ cdot a_n}](../../images/99/9944.png) ( moyenne géométrique),
( moyenne géométrique),
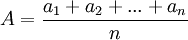 ( moyenne arithmétique ),
( moyenne arithmétique ),
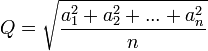 ( moyenne quadratique).
( moyenne quadratique).
Les inégalités de pouvoir
Parfois avec la notation "l'inégalité de pouvoir" comprendre les inégalités qui contiennent  expressions de type cas
expressions de type cas 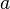 et
et  sont des nombres réels positifs ou expressions de certaines variables. Elles peuvent apparaître à des exercices de olympiades mathématiques et des calculs.
sont des nombres réels positifs ou expressions de certaines variables. Elles peuvent apparaître à des exercices de olympiades mathématiques et des calculs.
Exemples
- Si
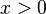 , Puis
, Puis 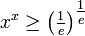
- Si
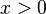 , Puis
, Puis 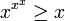
- Si
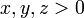 , Puis
, Puis 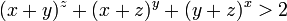 .
. - Pour toute nombres réels distincts
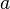 et
et  ,
, 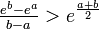
- Si
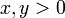 et
et 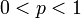 , Puis
, Puis 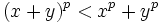
- Si
 ,
, 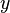 et
et 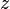 sont positifs, alors
sont positifs, alors 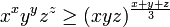
- Si
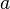 et
et  sont positifs, alors
sont positifs, alors 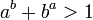 . Ce résultat a été généralisé par R. Ozols en 2002 qui a prouvé que si
. Ce résultat a été généralisé par R. Ozols en 2002 qui a prouvé que si 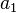 ,
, 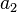 , ...,
, ..., 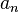 sont des nombres réels positifs, puis
sont des nombres réels positifs, puis 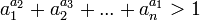 (Résultat est publié dans trimestrielle vulgarisation scientifique lettone le ciel étoilé, voir les références).
(Résultat est publié dans trimestrielle vulgarisation scientifique lettone le ciel étoilé, voir les références).
Inégalités bien connus
Voir également liste des inégalités.
Les mathématiciens utilisent souvent les inégalités à des quantités consolidés pour lesquels les formules exactes ne peuvent pas être calculés facilement. Certaines inégalités sont utilisés si souvent qu'ils ont des noms:
- Inégalité d'Azuma
- Inégalité de Bernoulli
- Inégalité de Boole
- Inégalité de Cauchy-Schwarz
- L'inégalité de Tchebychev
- Inégalité de Chernoff
- Cramér-Rao inégalités
- Inégalité de Hoeffding
- L'inégalité de Hölder
- Inégalité arithmético-géométrique
- L'inégalité de Jensen
- L'inégalité de Kolgomorov
- L'inégalité de Markov
- Minkowski inégalités
- Inégalité de Nesbitt
- L'inégalité de Pedoe
- Triangle inégalités
Les mnémoniques pour les étudiants
Les jeunes étudiants confondent parfois la moins-que et de signes supérieur, qui sont des images miroir l'une de l'autre. Un moyen mnémotechnique couramment enseignée est que le signe représente la bouche d'une faim alligator qui essaie de manger le plus grand nombre; ainsi, il se ouvre à la fois vers 8 3 <8 et 8> 3. Une autre méthode est de remarquer la quantité de points de plus grandes à la plus petite quantité et dit, "ha-ha, je suis plus grand que vous."
En outre, sur une ligne numérique horizontale, le signe supérieur est la flèche qui est à l'extrémité la plus grande de la ligne numéro. De même, le symbole est inférieure à la flèche à l'extrémité la plus petite de la numéro de ligne (<--- 0--1--2--3--4--5--6--7--8--9 --->).
Les symboles peuvent aussi être interprétés directement à partir de leur forme - le côté avec une grande séparation verticale indique une grande (r) la quantité, et le côté qui est un point indique un petit (er) la quantité. De cette manière, les symboles d'inégalité sont semblables à la musique crescendo et decrescendo. Les symboles pour l'égalité, moins-que ou égal à, et supérieur ou égal à peuvent aussi être interprétés avec cette perspective.
Les nombres complexes et les inégalités
En introduisant un ordre lexicographique sur les nombres complexes , ce est un ensemble totalement ordonné. Toutefois, il est impossible de définir ≤ sorte que 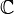 , +, *, Devient un ≤ corps ordonné. Si
, +, *, Devient un ≤ corps ordonné. Si 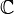 , +, *, ≤ étaient une corps ordonné, il doit satisfaire les deux propriétés suivantes:
, +, *, ≤ étaient une corps ordonné, il doit satisfaire les deux propriétés suivantes:
- si un ≤ b alors a + c ≤ b + c
- si 0 ≤ a et 0 ≤ b ≤ 0 alors ab
Parce ≤ est un total de la commande, pour un certain nombre a, a ≤ 0 ou 0 ≤ a. Dans les deux cas 0 ≤ a 2; cela signifie que 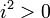 et
et 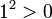 ; si
; si 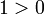 et
et 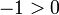 , Contradiction.
, Contradiction.
Cependant ≤ peut être défini afin de satisfaire la première propriété, ce est à dire si un ≤ b alors a + c ≤ b + c. Une définition qui est parfois utilisé est l'ordre alphabétique:
- a ≤ b si
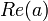 <
< 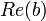 ou (
ou (  et
et 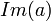 ≤
≤ 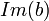 )
)
Il peut facilement être prouvé que cette définition a ≤ b alors a + c ≤ b + c


