
Entier
À propos de ce écoles sélection Wikipedia
SOS Enfants, qui se déroule près de 200 sos écoles dans le monde en développement, a organisé cette sélection. Avec enfants SOS vous pouvez choisir de parrainer des enfants dans plus de cent pays

Les entiers (du latin entier, ce qui signifie avec intégrité intacte, ensemble, ensemble) sont l'ensemble des nombres composés des nombres naturels dont 0 ( 0 , 1 , 2, 3, ...) et leurs négatifs (0, -1, -2, -3, ...). Ils sont des nombres qui peuvent être écrits sans composante fractionnaire ou décimal, et se inscrivent dans l'ensemble {... -2, -1, 0, 1, 2, ...}. Par exemple, 65, 7 et -756 sont des nombres entiers; 1,6 1½ et ne sont pas des nombres entiers. En d'autres termes, les entiers sont les numéros que vous pouvez compter avec des éléments tels que les pommes ou vos doigts, et leurs négatifs, y compris 0.
Plus formellement, les entiers sont le seul domaine intégrante dont les éléments sont positifs bien ordonné, et dans quel ordre est préservée par ailleurs . Comme les nombres naturels, les entiers forment un ensemble infini dénombrable. Le ensemble des entiers est souvent notée par un gras Z (ou tableau noir gras 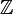 , Unicode U + 2124), ce qui signifie Zahlen ( allemand pour les numéros).
, Unicode U + 2124), ce qui signifie Zahlen ( allemand pour les numéros).
En théorie algébrique des nombres, ces entiers communément comprises, intégré dans le domaine des nombres rationnels , sont appelés entiers rationnels pour les distinguer de la définition plus large entiers algébriques.
Propriétés algébriques
Comme les nombres naturels, Z est fermé sous la opérations de plus et la multiplication , à savoir la somme et le produit de toutes les deux des nombres entiers est un nombre entier. Cependant, avec l'inclusion des nombres naturels négatifs, et, surtout, zéro , Z (à la différence des nombres naturels) est également fermé en vertu de soustraction . Z ne est pas fermé en vertu de l'opération de division , étant donné que le quotient de deux nombres entiers (par exemple, une divisé par 2), ne est pas nécessairement un nombre entier.
Les listes suivantes certains des propriétés de base d'addition et de multiplication pour des entiers a, b et c.
| addition | multiplication | |
| fermeture: | a + b est un nombre entier | a × b est un nombre entier |
| associativité : | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) x c |
| commutativité : | a + b = b + a | a × b = b × a |
| existence d'un élément de l'identité: | a + 0 = a | a × 1 = a |
| existence de éléments inverses: | a + (- a) = 0 | |
| distributivité: | a × (b + c) = (a × b) + (a × c) | |
| Aucun diviseurs de zéro: | si ab = 0, soit a = 0 ou b = 0 (ou les deux) | |
Dans le langage de l'algèbre abstraite , les cinq premières propriétés énumérées ci-dessus pour plus disent que Z est une vertu plus groupe abélien. En tant que groupe pour l'addition, Z est un groupe cyclique , puisque chaque nombre entier différent de zéro peut être écrite comme une somme finie 1 + 1 + 1 ... ou (-1) + (-1) + ... + (-1) . En effet, plus Z est sous le seul groupe cyclique infini, en ce sens que ne importe quel groupe cyclique est infini isomorphe à Z.
Les quatre premières propriétés énumérées ci-dessus pour la multiplication disent que Z sous la multiplication est un monoïde commutatif. Toutefois, notez que pas tout entier a un inverse multiplicatif; par exemple il ne est pas entier x tel que 2 x = 1, parce que le côté gauche est encore, tandis que le côté droit est impair. Cela signifie que pour la multiplication Z ne est pas un groupe.
Toutes les règles de la table de propriété ci-dessus, à l'exception de la dernière, pris ensemble disent que Z avec addition et la multiplication est commutative anneau avec l'unité. Ajout de la dernière propriété dit que Z est un intègre. En fait, Z fournit la motivation pour définir une telle structure.
L'absence d'inverses multiplicatifs, ce qui correspond au fait que Z ne est pas fermé sous division, signifie que Z ne est pas un domaine. Le plus petit champ contenant les entiers est le domaine des nombres rationnels . Ce processus peut être imité pour former le corps des fractions de ne importe quel domaine intégrante.
Bien que la division ordinaire ne est pas défini sur Z, il ne possède une propriété importante appelé algorithme de division: ce est-à donné deux entiers a et b avec b ≠ 0, il existe des entiers uniques q et r tel que a = q × b + r et 0 ≤ r <| b |, où | b | désigne la valeur absolue de b. L'entier q est appelé le quotient et r est appelé le reste, résultant de la division de a par b. Ce est la base de la Algorithme d'Euclide pour calculer plus grands communs diviseurs .
Là encore, dans la langue de l'algèbre résumé, le dit ci-dessus que Z est un Domaine euclidienne. Cela implique que Z est un anneau principal et un entier positif peuvent être écrites que les produits de nombres premiers d'une manière essentiellement unique. Ce est le théorème fondamental de l'arithmétique .
Ordre théorie propriétés
Z est un ensemble totalement ordonné sans supérieure ou inférieure. L'ordre des Z est donnée par
- ... <-2 <-1 <0 <1 <2 <...
Un entier est positif se il est supérieur à zéro et négative si elle est inférieure à zéro. Zéro est définie comme ni négative ni positive.
L'ordre des nombres entiers est compatible avec les opérations algébriques de la manière suivante:
- si a <b et c <d, alors a + c <b + d
- si a <b et 0 <c, alors ac <bc. (De ce fait, on peut montrer que si c <0, alors ac> Colombie-Britannique.)
Il se ensuit que Z avec la commande ci-dessus est un anneau commandé.
Construction
Les entiers peuvent être construits à partir des nombres naturels en définissant classes d'équivalence des paires de nombres naturels N × N en vertu d'une relation d'équivalence , "~", où
précisément lorsque
Prenant 0 être un nombre entier naturel, les nombres naturels peuvent être considérés comme des entiers par la enrobage que les cartes à n [(n, 0)], où [(a, b)] désigne la classe d'équivalence ayant (a, b) en tant que membre.
Addition et la multiplication de nombres entiers sont définis comme suit:
Il est facile de vérifier que le résultat est indépendant du choix des représentants des classes d'équivalence.
Typiquement, [(a, b)] est indiqué par
où
Si les nombres naturels sont identifiés avec les entiers correspondants (en utilisant le plongement mentionné ci-dessus), cette convention ne crée aucune ambiguïté.
Cette notation récupère le familier représentation des nombres entiers comme {..., - 3, -2, -1,0,1,2,3, ...}.
Certains exemples sont les suivants:
Entiers de l'informatique
Un entier (parfois appelé un "int", du nom d'un type de données dans le langage de programmation C ) est souvent une primitive type de données en langages informatiques . Cependant, les types de données entières ne peuvent représentent un sous-ensemble de tous les entiers, puisque les ordinateurs sont des pratiques capacité finie. En outre, dans le courant complément de la représentation des deux, la définition inhérente signe une distinction entre «négative» et «non-négatif» plutôt que «négatif, positif, et 0". (Il est cependant tout à fait possible pour un ordinateur afin de déterminer si une valeur de nombre entier est vraiment positif).
Représentations de longueur variable d'entiers, tels que bignums, peut stocker ne importe quel nombre entier qui se inscrit dans la mémoire de l'ordinateur. D'autres types de données de nombres entiers sont mis en oeuvre avec une taille fixe, en général un nombre de bits qui est une puissance de 2 (4, 8, 16, etc.) ou un certain nombre de chiffres décimaux mémorable (par exemple, 9 ou 10).
En revanche, les modèles théoriques de calculateurs numériques , tels que Machines de Turing, ne ont généralement pas infinie (mais seulement sans limite finie) capacités.
Cardinalité
Le cardinalité de l'ensemble d'entiers est égale à 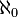 . Cela est aisément démontrée par la construction d'un bijection, ce est une fonction qui est injective et surjective de
. Cela est aisément démontrée par la construction d'un bijection, ce est une fonction qui est injective et surjective de 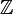 à
à 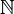 . Considérons la fonction
. Considérons la fonction
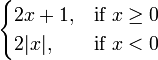 .
.
Si le domaine est limité à 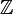 puis chaque membre du
puis chaque membre du 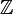 a un et un seul membre correspondant de
a un et un seul membre correspondant de 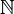 et par la définition de l'égalité cardinal les deux ensembles ont le même cardinal.
et par la définition de l'égalité cardinal les deux ensembles ont le même cardinal.

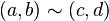
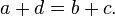
![[(A, b)] + [(C, D)]:. = [(A + c, b + d)] \,](../../images/94/9425.png)
![[(A, b)] \ cdot [(c, d)]:. = [(Ca + bd, ad + bc)] \,](../../images/94/9426.png)
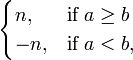
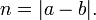
![\ Begin {align} 0 & = [(0,0)] = & [(1,1)] = & \ cdots & & = [(k, k)] \\ & 1 = [(1,0)] & = [(2,1)] = & \ & & cdots = [(k + 1, k)] -1 & \\ = [(0,1)] & = [(1,2)] = & \ cdots & & = [(k, k + 1)] 2 & \\ = [(2,0)] & = [(3,1)] = & \ & & cdots = [(k + 2, k)] \\ & -2 = [(0,2)] = & [(1,3)] = & \ cdots & & = [(k, k + 2)] \ end {align}](../../images/94/9429.png)
