
théorie des nœuds
Contexte des écoles Wikipédia
Cette sélection Wikipedia est déconnecté disponibles à partir enfants SOS pour la distribution dans le monde en développement. Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/


théorie des nœuds est la mathématique branche de topographie études noeuds mathématiques, qui sont définis en tant que plongements d'un cercle en trois dimensions espace euclidien , R 3. Ce est essentiellement l'équivalent d'un classique chaîne nouée avec les extrémités se sont réunis pour l'empêcher de devenir annulée. Deux noeuds mathématiques sont équivalentes si l'on peut être transformé en l'autre par une déformation de R 3 sur lui-même (également dénommée isotopie ambiante); ces transformations correspondent à des manipulations d'une chaîne nouée qui ne impliquent pas couper la chaîne ou passer la ficelle par lui-même.
Noeuds peuvent être décrits dans diverses décisions. Compte tenu de la méthode de raison, cependant, il peut y avoir plus d'une description, représente le même noeud. Par exemple, un procédé commun de décrire un noeud est un schéma planaire. Mais ne importe quel noeud donné peut être établi de plusieurs façons différentes en utilisant un schéma de plan. Par conséquent, un problème fondamental dans la théorie des nœuds est de déterminer quand deux descriptions représentent le même noeud. Une manière de distinguer les noeuds consiste à utiliser un Invariant de nœuds, une «quantité» qui reste le même, même avec différentes descriptions d'un noeud.
Le concept d'un noeud a été étendue à des dimensions supérieures en considérant n sphères de dimension m de dimension dans l'espace euclidien. Cette a été étudiée plus activement dans la période 1960-1980, quand un certain nombre d'avancées ont été faites. Ces dernières années, phénomènes de basse dimensionnalité ont suscité le plus d'intérêt.
Recherche en théorie des nœuds a commencé avec la création de tableaux de nœuds et la présentation systématique de noeuds. Alors que la tabulation reste une tâche importante, les chercheurs d'aujourd'hui ont une grande variété de milieux et de buts. La théorie des nœuds classique, comme initié par Max Dehn, JW Alexander, et d'autres, est principalement lié à la groupe de noeud et invariants de théorie d'homologie tel que le Polynôme d'Alexander.
La découverte de la Polynomiale Jones par Vaughan Jones en 1984, et les contributions ultérieures de Edward Witten, Maxim Kontsevich, et d'autres, ont révélé des liens profonds entre la théorie des nœuds et des méthodes mathématiques en mécanique statistique et de la théorie quantique des champs . Une pléthore de invariants de nœuds ont été inventées depuis lors, en utilisant des outils sophistiqués tels que groupes quantiques et Homologie de Floer.
Au cours des 30 dernières années, la théorie des nœuds est également devenu un outil en mathématiques appliquées. Les chimistes et les biologistes utilisent la théorie des nœuds de comprendre, par exemple, chiralité des molécules et les actions de enzymes sur l'ADN .
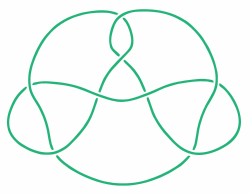
Histoire
Noeuds ont été étudiés par Carl Friedrich Gauss , qui a développé le Gauss liaison intégrale pour calculer la reliant nombre de deux noeuds. Son élève Johann Benedict Listing, après qui Le noeud de Listing est nommé, favorisé leur étude. Le stimulus début important dans la théorie des nœuds arriverait plus tard avec Sir William Thomson (Lord Kelvin) et sa théorie d'atomes de vortex. (Sossinsky 2002, p. 1-3)

En 1867, après avoir observé écossaise physicien Les expériences de Peter Tait impliquant des ronds de fumée, Thomson sont venus à l'idée que les atomes étaient nœuds de tourbillonner tourbillons dans le æther . Les éléments chimiques correspondraient ainsi à noeuds et liens. Les expériences de Tait ont été inspirés par un document de Helmholtz sur vortex toriques dans les fluides incompressibles. Thomson et Tait croyaient que la compréhension et la classification de tous les nœuds possibles seraient expliquer pourquoi atomes absorbent et émettent de la lumière à seulement discret longueurs d'onde ce qu'ils font. Par exemple, Thomson pense que pourrait être le sodium Hopf lien en raison de ses deux lignes de spectres. (Sossinsky 2002, p. 3-10)
Tait a ensuite commencé liste noeuds uniques dans la croyance qu'il créait une table d'éléments. Il a formulé ce qui est maintenant connu sous le nom Tait conjecture sur noeuds alternées. (Les conjectures ont finalement été résolus dans les années 1990). Les tableaux de nœuds de Tait ont ensuite été améliorées par CN Little et TP Kirkman. (Sossinsky 2002, p. 6)
James Clerk Maxwell , un collègue et ami de Thomson et Tait, a également développé un vif intérêt dans les noeuds. Maxwell a étudié le travail de Cotation en noeuds. Il a de nouveau interprété Gauss »reliant intégrante en termes de théorie électromagnétique. Dans sa formulation, l'intégrale représente le travail effectué par une particule chargée se déplaçant le long d'un composant de la liaison sous l'influence du champ magnétique généré par un courant électrique le long de l'autre composant. Maxwell a également poursuivi l'étude des anneaux de fumée en tenant compte de trois anneaux en interaction.
Lorsque l'éther luminifère n'a pas été détecté dans le Expérience de Michelson-Morley, la théorie de vortex est devenu complètement obsolète, et la théorie des nœuds a cessé d'être d'un grand intérêt scientifique. La physique moderne démontre que les longueurs d'onde discrètes dépendent les niveaux d'énergie quantique.
Suite au développement de la topologie dans le début du 20e siècle dirigé par Henri Poincaré, topologues tels que Max Dehn, JW Alexander, et Kurt Reidemeister, enquête noeuds. Sur ce sauta du Reidemeister se déplace et la Alexander polynomiale. (Sossinsky 2002, p. 15-45) a également développé Dehn Chirurgie de Dehn, qui portait noeuds à la théorie générale des variétés de dimension 3, et a formulé la Dehn problèmes dans la théorie des groupes , tels que le problème de mot. Pionniers dans la première moitié du 20e siècle comprennent Ralph Fox, qui a popularisé le sujet. Dans cette première période, la théorie des nœuds principalement composée d'étude dans le groupe de noeud et invariants de la homologiques noeud complément.
Quelques grandes découvertes à la fin du 20e siècle fortement relancé la théorie des nœuds. Le premier était Hyperbolisation théorème de Thurston qui a introduit la théorie de hyperboliques variétés de dimension 3 dans la théorie des nœuds et ont fait de première importance. Le travail de Thurston a également conduit, après beaucoup de l'expansion par d'autres, à l'utilisation efficace des outils de la théorie de la représentation et géométrie algébrique. Des résultats importants ont suivi, y compris le Gordon-Luecke théorème, qui a montré que nœuds ont été déterminées (jusqu'à réflexion miroir) par leurs compléments, et de la Conjecture Smith.
L'intérêt pour la théorie des nœuds de la communauté mathématique générale a augmenté de façon significative après La découverte de Vaughan Jones de la Polynôme Jones. Cela a conduit à d'autres polynômes de noeud comme le polynôme support, HOMFLY polynôme, et Polynomiale Kauffman. Jones a reçu la plus haute distinction en mathématiques, le Médaille Fields, en 1990 pour ce travail. (Sossinsky 2002, p. 71-89) En 1988, Edward Witten proposé un nouveau cadre pour le polynôme de Jones, en utilisant des idées existantes de la physique mathématique , comme Intégrales de chemin de Feynman, et l'introduction de nouvelles notions telles que la théorie topologique quantique des champs (Witten 1989). Witten a également reçu la médaille Fields, en 1990, en partie pour ce travail. La description de Witten du polynôme Jones implicite invariants liés pour 3-variétés. Les approches simultanées, mais différentes, par d'autres mathématiciens ont abouti à la Invariants Witten-Reshetikhin-Turaev et divers soi-disant " invariants quantiques », qui semblent être la version mathématiquement rigoureuse des invariants de Witten (Turaev 1994).
Au début des années 1990, invariants de nœuds qui englobent le polynôme Jones et ses généralisations, appelé invariants de type fini, ont été découverts par Vassiliev et Goussarov. Ces invariants, décrits initialement en utilisant des moyens topologiques "classiques", ont été montrés par la médaille Fields 1994 Maxim Kontsevich de résulter de l'intégration , en utilisant le Kontsevich intégrante, de certaines structures algébriques (Kontsevich 1993, Bar-Natan 1995).
Ces découvertes ont été suivies par la découverte de Khovanov homologie et noeud homologie de Floer, qui généralise considérablement les polynômes Jones et Alexander. Ces théories d'homologie ont contribué à poursuivre l'intégration de la théorie des nœuds.
Dans les dernières décennies du 20e siècle, les scientifiques et les mathématiciens ont commencé à trouver des applications de la théorie des nœuds à des problèmes dans la biologie et la chimie . théorie de noeud peut être utilisé pour déterminer si une molécule est chiral (a une "impartialité") ou non. Les composés chimiques de chiralité différente peuvent avoir des propriétés radicalement différentes, thalidomide est un exemple notable de cette. Plus généralement, noeud méthodes théoriques ont été utilisés dans l'étude topo-isomères, topologiquement différents arrangements de la même formule chimique. La théorie étroitement lié les écheveaux ont été effectivement utilisés dans l'étude de l'action de certaines enzymes de l'ADN. (Flapan 2000)
Knot équivalence
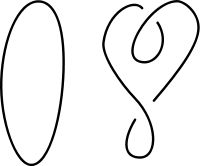
Un nœud est créé en commençant par un de un segment de ligne dimensionnelle, l'enroulant autour de lui-même de manière arbitraire, et ensuite la fusion de ses deux extrémités libres ensemble pour former une boucle fermée. Lorsque topologues mathématiques considèrent noeuds et autres enchevêtrements tels que liens et tresses, ils décrivent la manière dont le noeud est disposé dans l'espace autour de lui, appelé le l'espace ambiant. Si le nœud peut être déplacé en douceur, sans couper ou passant un segment par un autre, jusqu'à ce qu'il coïncide avec un autre noeud, les deux noeuds sont considérés comme équivalents. L'idée de l'équivalence noeud est de donner une définition précise du moment où deux incorporations doivent être considérés de la même.
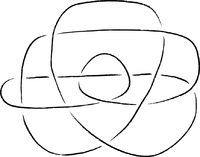
Le problème de base de la théorie des nœuds, le problème de reconnaissance, peut donc être déclaré:. Donné deux noeuds, de déterminer si elles sont équivalentes ou non algorithmes existent pour résoudre ce problème, avec la première donnée par Wolfgang Haken. Néanmoins, ces algorithmes utilisent de très nombreuses étapes, et un enjeu majeur dans la théorie est difficile de comprendre comment ce problème est vraiment (Hass 1997). Le cas particulier de la reconnaissance du dénouer, appelé dénouant problème, est d'un intérêt particulier.
diagrammes de Knot
Un moyen utile pour visualiser et manipuler noeuds est de projeter le nœud sur un plan-penser le nœud jetant une ombre sur le mur. Une petite perturbation dans le choix de la projection se assurer qu'il est un-à-un sauf aux points doubles, appelés passages à niveau, où «l'ombre» du nœud se croise une fois transversalement (Rolfsen 1976). A chaque passage, nous devons indiquer quelle section est "plus" et qui est "sous", de manière à être en mesure de recréer le nœud d'origine. Cela se fait souvent en créant une rupture dans le brin d'aller en dessous.
se déplace Reidemeister
En 1927, en collaboration avec cette forme schématique de noeuds, JW Alexander et GB Briggs, et indépendamment Kurt Reidemeister, a montré que deux diagrammes de noeud appartenant au même nœud peuvent être liés par une séquence de trois types de mouvements sur le diagramme, montré ci-dessous. Ces opérations, maintenant appelés les mouvements Reidemeister, sont:
- Tordre et détordre dans les deux sens.
- Déplacer un brin complètement sur une autre.
- Déplacer un brin complètement sur ou sous un pont.
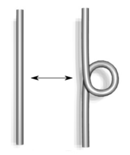 | 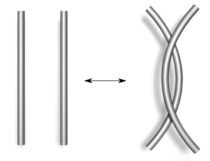 |
| Type I | Type II |
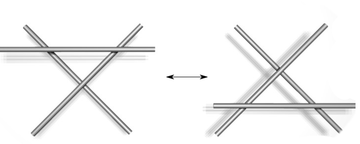 | |
| Type III | |
invariants Knot
Un invariant de noeud est une «quantité», ce est la même chose pour noeuds équivalents (Adams 2001, Lickorish 1997, Rolfsen 1976). Un invariant peut prendre la même valeur sur les deux noeuds différents, donc par lui-même peut être incapable de distinguer tous les noeuds. Un invariant élémentaire est tricolorability.
"Classique" invariants de nœuds sont les groupe de noeuds, qui est la groupe fondamental de la noeud complément, et Polynôme d'Alexander, qui peut être calculée à partir de l'invariant Alexander, un module construit à partir de la couverture infini cyclique du complément de noeud (Lickorish 1997, Rolfsen 1976). Dans la fin du 20e siècle, invariants tels que «quantiques» polynômes invariants de noeuds et hyperboliques ont été découverts. Ces invariants susmentionnées ne sont que la pointe de l'iceberg de la théorie des nœuds moderne.
polynômes Knot
Un polynôme de noeud est un invariant de nœud qui est un polynôme . Des exemples bien connus incluent le Jones et Polynômes Alexander. Une variante du polynôme d'Alexander, la Alexander-Conway polynôme est un polynôme de la variable z avec entiers Lickorish coefficients (1997).
Supposons que nous sommes donné un schéma de liaison qui est orientée, ce est à dire tous les composants de la liaison a une direction privilégiée indiqué par une flèche. Supposons également 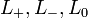 sont orientées diagrammes de liaison résultant de la modification du diagramme à un passage déterminé du diagramme, comme indiqué sur la figure:
sont orientées diagrammes de liaison résultant de la modification du diagramme à un passage déterminé du diagramme, comme indiqué sur la figure:
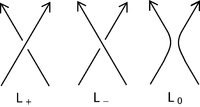
Alors le polynôme d'Alexander-Conway, C (z), est définie de manière récursive selon les règles:
- C (O) = 1 (où O est un diagramme de la dénouer)
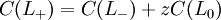
La deuxième règle est ce qui est souvent considéré comme un rapport écheveau. Pour vérifier que ces règles donnent un invariant, il faut déterminer que le polynôme ne change pas dans les trois mouvements Reidemeister. Beaucoup de polynômes de nœuds importants peuvent être définis de cette façon.
Ce qui suit est un exemple typique d'un calcul utilisant une relation écheveau. Il calcule le polynôme Alexander-Conway du Nœud de trèfle. Les taches jaunes indiquent l'endroit où nous avons appliqué la relation.
- C (
 ) = C (
) = C (  ) Z + C (
) Z + C (  )
)
donne l'dénouer et de la Lien Hopf. L'application de la relation avec le lien Hopf à l'endroit indiqué,
- C (
 ) = C (
) = C (  ) Z + C (
) Z + C (  )
)
donne un lien déformable à un avec 0 points de passage (ce est en fait la dissocier de deux composants) et une dénouer. Le unlink prend un peu de sournoiserie:
- C (
 ) = C (
) = C (  ) Z + C (
) Z + C (  )
)
ce qui implique que C (unlink de deux composants) = 0, puisque les deux premiers polynômes sont du dénouer et donc égale.
Mettre tout cela ensemble affiche:
- C (trèfle) = 1 + z (0 + z) = 1 + z 2
Depuis le polynôme d'Alexander-Conway est un invariant de noeud, ce qui montre que le trèfle ne est pas équivalente à la dénouer. Donc, le trèfle est vraiment "noué".
En fait, il ya deux noeuds trilobées, appelée la droite et trèfles gaucher, qui sont des images miroir de l'autre (prendre un diagramme du trèfle donnée ci-dessus et changer chaque passage à l'autre moyen d'obtenir l'image miroir). Ce ne sont pas équivalents entre eux! Ceci a été démontré par Max Dehn, avant l'invention des polynômes de nœuds, en utilisant des méthodes théoriques groupe (Dehn 1914). Mais le polynôme Alexander-Conway de chaque espèce de trèfle sera le même, comme on le voit en passant par le calcul ci-dessus avec l'image miroir. Le polynôme Jones peut en effet distinguer entre les noeuds de trèfle gauche et droitiers (Lickorish 1997).
Invariants hyperboliques
-
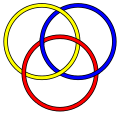
Le Anneaux Borromées sont un lien avec la propriété que la suppression d'un anneau délie les autres.
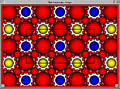
Aube de vue de snappea: la Anneaux Borromées complètent dans la perspective d'une vie habitant près de la composante rouge.
William Thurston se est avéré beaucoup de noeuds sont noeuds hyperboliques, ce qui signifie que le noeud complément, à savoir les trois points de l'espace non sur le noeud, admettre une structure géométrique, en particulier celle du géométrie hyperbolique. La structure hyperbolique dépend que du noeud de sorte que toute quantité calculée à partir de la structure hyperbolique est donc un invariant de noeud. (Adams 2001)
Géométrie permet de visualiser ce que l'intérieur d'un nœud ou un lien complément ressemble en imaginant des rayons de lumière que de voyager le long des géodésiques de la géométrie. Un exemple est fourni par l'image du complément de la Anneaux Borromées. L'habitant de ce lien complément visualise l'espace de près de la composante rouge. Les boules dans l'image sont vues de horoball quartiers de la liaison. En épaississant le lien d'une manière standard, on obtient ce qu'on appelle des quartiers horoball des composants de liaison. Même si la limite d'un des quartiers est un tore, vue par l'intérieur le lien complément, il ressemble à une sphère, appelée horoball. Chaque composant de liaison apparaît comme une infinité de horoballs (d'une couleur) qu'il ya une infinité de rayons lumineux de l'observateur à la composante de lien. Le parallélogramme fondamentale (qui est indiqué dans l'image), carreaux à la fois verticalement et horizontalement.
Le modèle de horoballs est lui-même un invariant utile. Autres invariants hyperboliques comprennent la forme de la paralleogram fondamentale, la longueur de géodésique le plus court, et le volume. Efforts de nœuds et un lien tabulation modernes ont utilisé ces invariants efficacement. Ordinateurs rapides et les méthodes intelligentes de l'obtention de ces invariants font le calcul de ces invariants, dans la pratique, une tâche simple. (Adams, Hildebrand, et Weeks, 1991)
Dimensions supérieures
En quatre dimensions, toute boucle fermée de chaîne unidimensionnelle est équivalente à une dénouer. On peut réaliser la déformation nécessaire en deux étapes. La première étape consiste à "pousser" la boucle dans un sous-espace à trois dimensions, ce qui est toujours possible, bien que d'expliquer technique. La deuxième étape est en train de changer passages. Supposons un brin est derrière un autre comme on le voit à partir d'un point choisi. Soulevez-le dans la quatrième dimension, il n'y a donc pas d'obstacle (le brin avant ayant aucun composant il); puis faites glisser vers l'avant, et déposez-le dos, maintenant devant. Une analogie pour le plan serait une chaîne de levage jusqu'à la surface.
Depuis un nœud peut être considéré comme topologiquement une sphère de dimension 1, la prochaine généralisation est d'envisager une sphère bidimensionnelle embarqué dans une sphère quatre dimensions. Une telle intégration est dénoua se il est un homéomorphisme de la sphère 4 sur lui-même en prenant la 2-sphère à un "rond" 2-sphère standard. Noeuds suspension et noeuds filés sont deux familles typiques de ces noeuds 2-sphère.
La technique mathématique appelée "position générale" implique que, pour un n donné -sphere dans le m -sphere, si m est suffisamment grande (en fonction de n), la sphère doit être dénoua. En général, linéaire par morceaux sphères n- former des noeuds que dans (n 2) (-space Christopher Zeeman 1963), bien que ce ne est plus une exigence pour les sphères en douceur noués. En fait, il ya en douceur noués 4k-1 -Sphères dans -espace 6k, par exemple il ya une douceur noués 3-sphère dans la 6-sphère (Haefliger 1962, Levine 1965). Ainsi la codimension d'un nœud lisse peut être arbitrairement grand lorsqu'il ne est pas la fixation de la dimension de la sphère noués; Cependant, tout k -sphere lisse dans un n -sphere à 2n-3k-3> 0 est dénoua. La notion d'un noeud a d'autres généralisations en mathématiques, voir: noeud (mathématiques).
Ajout de noeuds
Deux nœuds peuvent être ajoutés en coupant les deux nœuds et de rejoindre les paires d'extrémités. Cela peut être formellement défini comme suit (Adams 2001): envisager une projection plane de chaque nœud et supposent ces projections sont disjoints. Trouver un rectangle dans le plan où une paire de côtés opposés sont arcs le long de chaque noeud tandis que le reste du rectangle est disjointe de les noeuds. Former un nouveau noeud par suppression de la première paire de côtés opposés et attenant à l'autre paire de côtés opposés. Le nœud qui en résulte est la somme des noeuds d'origine.
Cette opération se appelle la somme de noeud, ou parfois la somme connectée ou la composition des deux noeuds. La somme de noeud est commutative et associative . Il ya aussi une décomposition de choix pour un nœud qui nous permet de définir un premier ou composé noeud, analogue à premiers numéros et composites. Le nœud de trèfle est le plus simple Premier noeud. Nœuds de dimensions supérieures peuvent être ajoutés par épissage des n-sphères. Bien que vous ne pouvez pas former le dénouer en trois dimensions en ajoutant deux noeuds non-triviales, vous pouvez en dimensions supérieures, au moins si l'on considère noeuds lisses dans codimension au moins trois.
noeuds Totaliser
Traditionnellement, les noeuds ont été catalogués en termes de Crossing Number. Le nombre de nœuds non triviales d'un certain nombre de passage donnée augmente rapidement, ce qui rend difficile tableaux de calcul. tables de Knot comprennent généralement seulement noeuds principaux et une seule entrée pour un noeud et son image miroir (même se ils sont différents). La séquence du nombre de noeuds principaux d'un certain nombre de passage donnée, jusqu'à numéro de passage 16, est égal à 0, 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46972 , 253293, 1388705 ... (séquence A002863 dans OEIS ). Alors que limites supérieures et inférieures exponentielles pour cette séquence sont connus, il n'a pas été prouvé que cette séquence est strictement croissante (Adams, 2001).
Les premières tables de noeud par Tait, Little, et Kirkman utilisés diagrammes de noeud, même si Tait également utilisé un précurseur de la Dowker notation. Différentes notations ont été inventé pour nœuds qui permettent tabulation plus efficace.
Les premiers tableaux ont tenté de répertorier tous les noeuds d'au plus 10 passages à niveau, et tous les noeuds alternées de 11 passages. Le développement de la théorie des nœuds en raison de Alexander, Reidemeister, Seifert, et d'autres facilité la tâche de vérification et de tableaux de nœuds jusqu'à et y compris 9 passages ont été publiés par Alexander-Briggs et Reidemeister à la fin des années 1920.
La première vérification majeur de ce travail a été fait dans les années 1960 par John Horton Conway, qui non seulement a développé une nouvelle notation mais aussi le Alexander-Conway polynomiale (Conway 1970, Doll-Hoste 1991). Ce vérifié la liste des noeuds d'au plus 11 postes et une nouvelle liste de liens jusqu'à 10 passages. Conway a trouvé un certain nombre d'omissions, mais seulement une duplication dans les Tait-petites tables; Mais il a raté les doublons appelé le Perko paire, qui ne puisse être remarqué en 1974 par Kenneth Perko (Perko 1974). Cette erreur se propagerait célèbre quand Dale Rolfsen ajouté une table de noeud dans son texte influent, basée sur le travail de Conway.
Notation Alexander-Briggs
Ce est la notation la plus traditionnelle, en raison de le papier de 1927 JW Alexander et G. Briggs et plus tard étendu par Dale Rolfsen dans sa table de noeud. La notation organise simplement nœuds par leur numéro de passage. On écrit le nombre de passage avec un indice pour désigner son ordre parmi tous les noeuds avec ce numéro de passage. Cette commande est arbitraire et n'a donc pas de signification particulière.
La notation Dowker
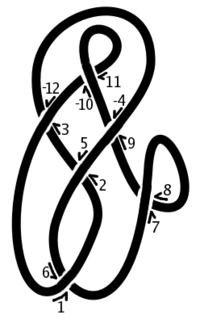
La notation Dowker, également appelé la notation ou un code Dowker-Thistlethwaite, pour un noeud est une séquence finie d'entiers pairs. Les numéros sont générés en suivant le nœud et le marquage des passages avec entiers consécutifs. Depuis chaque passage est visité deux fois, ce qui crée un appariement de même avec entiers impairs. Un signe approprié est donné pour indiquer encore et sousterrain. Par exemple, sur la figure le diagramme de noeud possède des passages marqués avec les paires (1,6) (3, -12) (5,2) (7,8) (9, -4) et (11, -10). La notation pour cette Dowker étiquetage est la séquence: 6 -12 2 8 -4 -10. Un diagramme de nœud a plus d'une notation Dowker possible, et il existe une ambiguïté bien comprise lors de la reconstruction d'un noeud à partir d'une notation Dowker.
Notation Conway
La notation Conway pour nœuds et liens, nommé d'après John Horton Conway, est basé sur la théorie de la enchevêtrements (Conway 1970). L'avantage de cette notation est qu'elle reflète certaines propriétés du noeud ou un lien.
La notation décrit comment construire un lien schéma particulier de la liaison. Commencez avec un polyèdre de base, un 4-valent plane connecté graphe sans Digon régions. Un tel premier polyèdre est notée par le nombre de sommets alors un certain nombre d'astérisques qui déterminent la position du polyèdre sur une liste de polyèdre de base. Par exemple, 10 ** désigne la deuxième polyèdre 10-sommet sur la liste de Conway.
Chaque sommet a alors une enchevêtrement algébrique substitué en elle (chaque sommet est orienté de sorte qu'il n'y a pas choix arbitraire en remplacement). Chaque tel enchevêtrement a une notation composée de chiffres et de signes + ou -.
Un exemple est une * 2 -3 2. Le 1 * désigne le seul polyèdre de base 1-sommet. Le 2 -3 2 est une séquence décrivant la fraction continue associée à un enchevêtrement rationnelle. On insère cet enchevêtrement au sommet du polyèdre de base 1 *.
Un exemple plus complexe est de 8 * 3.1.2 0.1.1.1.1.1 Là encore 8 * se réfère à un polyèdre de base avec 8 sommets. Les périodes séparent la notation pour chaque enchevêtrement.
Tout lien admet une telle description, et il est clair que ce est une notation très compact même pour très grand nombre de passage. Il ya quelques autres raccourcis habituellement utilisés. Le dernier exemple est généralement écrit 8 * 3: 2 0, où nous avons omis les uns et gardé le nombre de points à l'exception des points à la fin. Pour un nœud algébrique comme dans le premier exemple, 1 * est souvent omis.
Papier pionnier de Conway sur le sujet répertorie jusqu'à 10 vertex polyèdres base dont il utilise pour compiler des liens, qui sont devenus la norme pour ces liens. Pour une nouvelle liste de plus de polyèdres sommet, il ya des choix non standard disponibles.

