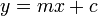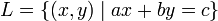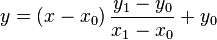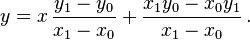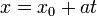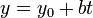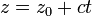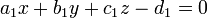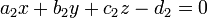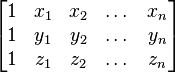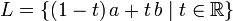Ligne (géométrie)

Trois lignes - les lignes rouges et bleues ont la même pente, tandis que les rouges et verts ont la même ordonnée à l'origine.

Une représentation d'une segment de ligne

Géométrie
Oxyrhynchus papyrus (P.Oxy. I 29) montrant fragment de Eléments d'Euclide
Histoire de la géométrie
Branches La géométrie euclidienne · La géométrie non-euclidienne · géométrie analytique · Géométrie riemannienne · Géométrie différentielle · La géométrie projective · Géométrie algébrique
Les domaines de recherche Géométrie algébrique · Géométrie différentielle · Géométrie symplectique
Concepts importants Remarque · Ligne · Perpendiculaire · Parallèlement · Le segment de ligne · Ray · Avion · Longueur · Espace · Volume · Vertex · Angle · Congruence · Similarité · Polygone · Triangle · Altitude · · Hypoténuse théorème de Pythagore · Quadrilatère · Trapèze · Kite · Parallélogramme ( Rhomboid, Rectangle, Rhombus, Place ) · Diagonal · Symétrie · Curve · Cercle · Zone d'un disque · Circonférence · Diamètre · Cylindre · Sphère · Pyramide · Dimensions ( une, deux, trois, quatre)
Géomètres Aryabhata · Ahmès · Apolonius · Archimède · Baudhayana · Bolyai · Brahmagupta · Euclid · Pythagore · Khayyám · Descartes · Pascal · Euler · Gauss · Ibn al-Yasamin · Jyeṣṭhadeva · Kâtyâyana · Lobachevsky · Manava · Minggatu · Riemann · Klein · Parameshvara · Poincaré · Al-Sijzi · Hilbert · Minkowski · Cartan · Veblen · Sakabe Kōhan · Gromov · Atiyah · Virasena · Yang Hui · Yasuaki Aida · Zhang Heng

La notion de la ligne ou une ligne droite a été introduit par les mathématiciens anciens pour représenter objets droites avec la largeur et la profondeur négligeable. Les lignes sont une idéalisation de ces objets. Ainsi, jusqu'au XVIIe siècle, les lignes ont été définies comme suit: "La ligne est la première espèce de quantité, qui a une seule dimension, à savoir la longueur, sans largeur ni la profondeur, et ne est rien d'autre que le débit ou la course du point qui [...] partira de son imaginaire déplacer quelque vestige de longueur, exonérée de toute la largeur. [...] La ligne droite est celle qui est aussi étendu entre ses points "

Euclid décrit une ligne comme "longueur de sans largeur", et a introduit plusieurs postulats indémontrables propriétés comme base à partir de laquelle il a construit la géométrie, qui se appelle maintenant la géométrie euclidienne pour éviter toute confusion avec d'autres géométries qui ont été introduites depuis la fin du XIXe siècle (tels que non euclidienne géométrie, la géométrie projective, et la géométrie affine).

En mathématiques modernes, étant donné la multitude de géométries, le concept d'une ligne est étroitement liée à la façon dont la géométrie est décrite. Par exemple, dans la géométrie analytique , une ligne dans le plan est souvent définie comme l'ensemble des points dont les coordonnées satisfaire une donnée équation linéaire , mais dans un cadre plus abstrait, comme géométrie incidence, une ligne peut être un objet indépendant, distinct de l'ensemble des points qui se trouvent sur elle.

Quand une géométrie est décrite par un ensemble de axiomes, la notion d'une ligne est généralement laissé indéfini (un soi-disant objet primitif). Les propriétés des lignes sont alors déterminés par les axiomes qui se rapportent à eux. Un avantage de cette approche est la flexibilité qu'il offre aux utilisateurs de la géométrie. Ainsi, dans la géométrie différentielle une ligne peut être interprété comme un géodésique (chemin le plus court entre les points), tandis que dans certaines géométries projectives une ligne est un espace vectoriel de dimension 2 (toutes les combinaisons linéaires de deux vecteurs indépendants). Cette flexibilité se étend également au-delà des mathématiques et, par exemple, permet aux physiciens de penser à la trajectoire d'un rayon lumineux comme étant une ligne.

Un segment de ligne est une partie d'une ligne qui est délimité par deux points d'extrémité distinctes et contient tous les points sur la ligne entre ses points d'extrémité. Selon la façon dont le segment de ligne est définie, l'un des deux points d'extrémité peuvent ou non faire partie du segment de ligne. Deux ou plusieurs segments de ligne peuvent avoir certains des mêmes relations que les lignes, comme étant parallèles, se croisant, ou l'inclinaison.

Définitions contre descriptions

Toutes les définitions sont finalement circulaire dans la nature car ils dépendent des concepts qui doivent eux-mêmes avoir des définitions, une dépendance qui ne peut être poursuivi indéfiniment sans revenir au point de départ. Pour éviter ce cercle vicieux certains concepts doivent être prises concepts primitifs; termes qui sont pas donné de définition. En géométrie, il est souvent le cas que la notion de ligne est prise comme primitive. Dans les cas où une ligne est un concept défini, comme dans la géométrie des coordonnées , quelques autres idées fondamentales sont prises comme primitives. Lorsque le concept de ligne est une primitive, le comportement et les propriétés des lignes sont dictées par la axiomes laquelle ils doivent satisfaire.

Dans un traitement axiomatique non axiomatique ou simplifiée de la géométrie, la notion d'une notion primitive peut être trop abstrait pour être traitées. Dans ce cas il est possible que la description ou l'image mentale d'une notion primitive est fourni pour donner une base pour construire la notion sur laquelle serait formellement être fondée sur les axiomes (implicites). Descriptions de ce type peuvent être appelés, par certains auteurs, que les définitions dans ce style informel de la présentation. Ce ne sont pas de véritables définitions et ne pouvaient pas être utilisés dans les preuves formelles de déclarations. La «définition» de la ligne dans les Eléments d'Euclide tombe dans cette catégorie. Même dans le cas où une géométrie spécifique est envisagée (par exemple, la géométrie euclidienne ), il ya un accord généralement acceptée parmi les auteurs à ce que une description informelle d'une ligne devrait être lorsque le sujet ne est pas traité formellement.

La géométrie euclidienne

Lorsque la géométrie a été formalisée par Euclide dans l' Elements , il a défini une ligne à être «longueur sans largeur" avec une ligne droite étant une ligne "qui se trouve uniformément avec les points sur elle-même». Ces définitions ne sont guère utiles car ils utilisent des termes qui ne sont pas, eux-mêmes, définies. En fait, Euclide n'a pas utilisé ces définitions dans ce travail et probablement les a inclus juste pour le rendre clair pour le lecteur ce qui a été discuté. Dans la géométrie moderne, une ligne est tout simplement considéré comme un objet ayant des propriétés données par axiomes, mais est parfois définie comme un ensemble de points obéissant à une relation linéaire lorsqu'une autre concept fondamental ne est pas définie.

Dans un formulation de la géométrie euclidienne évident, comme celui de Hilbert (axiomes d'Euclide originaux contenaient diverses failles qui ont été corrigées par les mathématiciens modernes), une ligne est déclarée présenter certaines propriétés dont il se rapportent à d'autres lignes et Le secteur. Par exemple, pour deux points distincts, il ya une ligne unique, les contenant et des deux lignes distinctes se coupent en au plus un point. En deux dimensions, à savoir la euclidienne plan , deux lignes ne se croisent pas sont appelés parallèle. En dimension supérieure, deux lignes qui ne se croisent pas peut être parallèle si elles sont contenues dans un plan , ou biaiser se ils ne sont pas.

Toute collecte d'un nombre fini de lignes partitionne le plan en polygones convexes (éventuellement illimitée); cette cloison est connu comme un disposition de lignes.

Rayon

Compte tenu d'une ligne et un point A sur elle, nous pouvons considérer que la décomposition A cette ligne en deux parties. Chacune de ces parties est appelée un rayon (ou demi-droite) et le point A est appelé son point initial. Le point A est considéré comme un membre du rayon. Intuitivement, un rayon est constitué de ces points sur une ligne passant par A et procédant indéfiniment, à partir de A, dans un seul sens le long de la ligne. Cependant, afin d'utiliser ce concept d'un rayon dans les preuves d'une définition plus précise est nécessaire.

Compte tenu des points distincts A et B, ils déterminent un rayon unique avec initial point A. En deux points définissent une ligne unique, ce rayon est constituée de tous les points entre A et B (y compris a et b) et tous les points C sur la droite passant par A et B tel que B est entre A et C. Ceci est parfois également exprimé comme l'ensemble de tous les points C tel que A ne est pas entre B et C. Un point D, sur la ligne déterminée par A et B, mais pas dans le rayon avec l'initiale point A déterminé par B, déterminera un autre rayon avec l'initiale point A. En ce qui concerne le rayon AB, AD rayon est appelée le rayon opposé.

Ainsi, nous dirions que deux points différents, A et B, définissent une ligne et une décomposition de cette ligne dans le union disjointe d'un segment ouvert (A, B) et deux rayons, BC et AD (point D ne est pas établi dans le diagramme, mais se trouve à gauche de A sur la ligne AB). Ce ne sont pas les rayons opposés car ils ont différents points initiaux.

La définition d'un rayon dépend de la notion de intermédiarité de points sur une ligne. Il se ensuit que les rayons ne existent que pour les géométries pour lesquelles cette notion existe, généralement la géométrie euclidienne ou la géométrie affine sur une corps ordonné. D'autre part, les rayons ne existent pas dans la géométrie projective ni dans une géométrie non sur une corps ordonné, comme les nombres complexes ou tout champ fini.

En topologie , un rayon dans un espace X est un plongement continue R ⁺ → X. Il est utilisé pour définir la notion importante de fin de l'espace.

Coordonner la géométrie

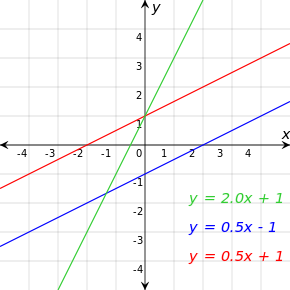
Dans la géométrie des coordonnées , les lignes d'un plan cartésien peuvent être décrites algébriquement par des équations linéaires . En deux dimensions, l'équation pour les lignes non-verticales est souvent donnée dans la forme d'une pente :

où:

m est le pente ou gradient de la ligne.

c est la ordonnée à l'origine de la ligne.

x est le variable indépendante de la fonction y = f (x).

La pente de la ligne par les points A (x _a, y _a) et B (x _b, y _b), lorsque X _a ≠ x _b, est donnée par m = _(b y -y _a) / _(b x -x _a) et de l'équation de cette droite peut se écrire y = m (x - x _a) + y _a.

Dans R ^2, chaque ligne L (y compris les lignes verticales) est décrite par une équation linéaire de la forme

avec de vrais fixe les coefficients a, b et c de telle sorte que a et b ne sont pas tous deux zéro. En utilisant ce formulaire, les lignes verticales correspondent aux équations avec b = 0.

Il existe de nombreuses variantes de manières d'écrire l'équation d'une droite qui peuvent tous être converti à partir d'un à l'autre par une manipulation algébrique. Ces formes (voir l'équation linéaire pour les autres formes) sont généralement nommés par le type d'informations (données) à propos de la ligne qui est nécessaire pour écrire la forme. Certaines des données importantes d'une ligne est sa pente, x à l'origine, points connus sur la ligne et ordonnée à l'origine.

L'équation de la droite passant par deux points différents 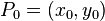et 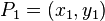peut se écrire

.

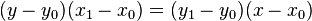Si x ₀ ≠ x _1, cette équation peut être réécrite comme

ou

En trois dimensions, les lignes ne peuvent pas être décrites par une seule équation linéaire, de sorte qu'ils sont souvent décrits par équations paramétriques:

où:

x, y et z sont tous des fonctions de la variable indépendante t qui se étend sur les nombres réels.

(X _0, y _0, z ₀₎ est un point quelconque de la ligne.

a, b, et c sont reliées à la pente de la droite, de telle sorte que le vecteur (a, b, c) est parallèle à la ligne.

Ils peuvent également être décrits comme des solutions simultanée de deux équations linéaires

tel que 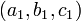et 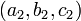ne sont pas proportionnelles (les relations 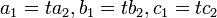impliquerait t = 0). Cela résulte en trois dimensions depuis une seule équation linéaire décrit généralement un plan et une ligne est ce qui est commun à deux plans d'intersection distincts.

Equation vectorielle

L'équation de vecteur de la ligne par les points A et B est donnée par r = OA + λ AB (où λ est un scalaire).

Si un vecteur est OA et OB b est un vecteur, alors l'équation de la ligne peut se écrire: r = a + λ (b - a).

Un rayon à partir du point A est décrite en limitant λ. Un rayon est obtenue si λ ≥ 0, et le rayon en face vient de λ ≤ 0.

Points alignés

Trois points sont dits être colinéaire se ils se trouvent sur la même ligne. Dans l'espace euclidien , trois points déterminent habituellement un plan , mais dans le cas de trois points alignés cela ne arrive pas.

Dans la géométrie des coordonnées , dans l'espace de dimension n des points X = (x _1, x _2, ..., x _n), Y = (y _1, y _2, ..., y _n), et Z = (z _1, z _2, ..., z _n) sont alignés si la matrice

a un classer inférieur à 3. En particulier, pour trois points dans le plan (n = 2), ci-dessus matrice est carrée et les points sont alignés si et seulement si son déterminant est nul.

Lorsque la distance d (a, b) entre deux points A et B est défini, la colinéarité entre trois points peut être exprimé par:

Les points a, b et c sont alignés si et seulement si d (x, a) = d (c, a) et d (x, b) = d (c, b) implique x = c.

En géométrie euclidienne cette propriété est vrai, car si c ne est pas sur la ligne déterminée par a et b, il y aura un autre point (pas égal à c) qui est tout aussi loin de a et b comme le point c est (visualiser le point de l'autre côté de la ligne qui est l'image miroir de c).

Dans les géométries où le concept d'une ligne est un notion primitive, comme peut être le cas dans certains géométries synthétiques, d'autres méthodes de détermination de colinéarité sont nécessaires.

Espace euclidien

Dans l'espace euclidien , R ⁿ (et analogue dans tous les autres espace affine), la ligne L passant par deux points différents de A et B (considéré comme vecteurs) est le sous-ensemble

La direction de la ligne est de a (t = 0) à b (t = 1), ou en d'autres termes, dans la direction du vecteur b - a. Différents choix de A et B peuvent produire la même ligne.

Types de lignes

Dans un sens, toutes les lignes de la géométrie euclidienne sont égaux, en ce que, sans coordonnées, on ne peut pas les distinguer les uns des autres. Cependant, les lignes peuvent jouer des rôles spéciaux par rapport à d'autres objets de la géométrie et être divisé en types selon cette relation. Par exemple, par rapport à une conique , les lignes peuvent être:

• lignes de Tangent ,
• Droites sécantes,
• Lignes extérieures, qui ne satisfont pas la conique à tout point du plan euclidien, ou plus spécialisées
• directrice .

Pour plus général courbes algébriques, les lignes pourraient également être:

• i -secant lignes, rencontrer la courbe aux points i compté sans la multiplicité, ou
• asymptotes.

En ce qui concerne triangles nous avons:

• la Euler ligne, et
• la Droites de Simson.

Pour un hexagone avec des sommets couché sur une conique nous avons la Pascal ligne et, dans le cas particulier où la conique est une paire de lignes, nous avons la ligne de Pappus.

La géométrie projective

Dans de nombreux modèles de la géométrie projective, la représentation d'une ligne rarement conforme à la notion de la «courbe droite», comme il est visualisé dans la géométrie euclidienne. En Géométrie elliptique nous voyons un exemple typique de cette. Dans la représentation de la géométrie sphérique elliptique, sont représentées par des lignes grands cercles de la sphère avec des points diamétralement opposés identifiés. Dans un autre modèle de géométrie elliptique, sont représentées par des lignes euclidiennes des plans passant par l'origine. Même si ces représentations sont visuellement distincts, ils répondent à toutes les propriétés (comme, deux points qui déterminent une gamme unique) qui les rendent représentations appropriées pour lignes dans cette géométrie.

Géodésiques

Le "rectitude" d'une ligne, interprété comme la propriété qu'il minimise les distances entre ses points, peut être généralisée et conduit à la notion de géodésiques dans espaces métriques.