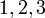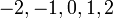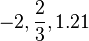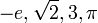Mathématiques

Euclid , mathématicien grec, 3ème siècle avant JC, comme imaginé par Raphaël dans ce détail de la L'École d'Athènes.

Mathématiques (familièrement, mathématiques ou mathématiques) est l'ensemble des connaissances centrée sur des concepts tels que la quantité , la structure, l'espace, et changer, et aussi la discipline académique qui les étudie. Benjamin Peirce a appelé «la science qui en tire les conclusions nécessaires". D'autres praticiens des mathématiques soutiennent que les mathématiques sont la science de modèle, et que les mathématiciens cherchent des patrons se trouve dans le nombre, l'espace, la science, ordinateurs, abstractions imaginaires, ou ailleurs. Mathématiciens explorer ces concepts, visant à formuler de nouvelles conjectures et établir leur vérité en rigoureux déduction choisi de manière appropriée axiomes et définitions.

Grâce à l'utilisation de abstraction et logique raisonnement, les mathématiques ont évolué à partir comptage, le calcul, la mesure et l'étude systématique de la formes et mouvements d'objets physiques. Connaissance et utilisation des mathématiques de base ont toujours été une partie intrinsèque et intégrante de la vie individuelle et collective. Raffinements des idées de base sont visibles dans les textes mathématiques originaires de la Egypte ancienne, Mésopotamienne, indienne , Chinois, Grec et Mondes islamiques. Arguments rigoureux première apparition dans Mathématiques grecques, notamment dans Euclide l ' Elements . Le développement se est poursuivi en rafales capricieuses jusqu'à la Renaissance période du 16ème siècle , lorsque les innovations mathématiques interagi avec le nouveau découvertes scientifiques, conduisant à une accélération de la recherche qui se poursuit jusqu'à nos jours.

Aujourd'hui, les mathématiques sont utilisées à travers le monde dans de nombreux domaines, y compris les sciences naturelles, l'ingénierie , la médecine et le sciences sociales telles que l'économie . mathématiques appliquées , l'application des mathématiques à des domaines tels, inspire et fait usage de nouvelles découvertes mathématiques et conduit au développement de nouvelles disciplines parfois entièrement. Les mathématiciens se engagent aussi dans mathématiques pures, ou mathématiques pour elle-même, sans avoir ne importe quelle application à l'esprit, bien que les demandes pour ce qui a commencé comme les mathématiques pures sont souvent découverts plus tard.

Étymologie

Le mot «mathématiques» (en grec: μαθηματικά ou mathēmatiká) vient du grec μάθημα (MATHEMA), ce qui signifie l'apprentissage, l'étude, la science, et de plus est venu d'avoir le sens de "étude mathématique" plus étroite et plus technique, même à l'époque classique. Son adjectif est μαθηματικός (mathēmatikós), liés à l'apprentissage, ou studieuse, qui même encore venu à signifier mathématique. En particulier, μαθηματικὴ τέχνη (mathēmatikḗ TEKHNE), en latin ars Mathematica, signifiait l'art mathématique.

Le pluriel apparente anglais , comme le français pluriel les mathématiques (et le singulier dérivé la mathématique moins couramment utilisées), remonte à la Mathematica pluriel neutre latine ( Cicero), sur la base du μαθηματικά de τα pluriel grec (ta mathēmatiká), utilisé par Aristote , et qui signifie à peu près «toutes choses mathématique". En anglais, cependant, les mathématiques nominaux prend des formes de verbe au singulier. Il est souvent abrégé en mathématiques en langue anglaise en Amérique du Nord et en mathématiques ailleurs.

Histoire

Un quipu, un dispositif de comptage utilisée par l' Inca .

L'évolution des mathématiques pourrait être considéré comme une série de plus en plus de abstractions, ou encore une expansion de la matière. La première abstraction était probablement celui de numéros . La réalisation que deux pommes et deux oranges ont quelque chose en commun était une percée dans la pensée humaine. En plus de reconnaître comment compter des objets physiques, peuples préhistoriques ont également reconnu la façon de compter quantités abstraites, comme le temps - jour , saisons , années. arithmétique ( addition , soustraction , multiplication et division ), ont naturellement suivi.

Des mesures supplémentaires doivent écriture ou d'un autre système pour les numéros d'enregistrement tels que pointages ou les cordes nouées appelés quipu utilisé par l' empire inca pour stocker des données numériques. numéral systèmes ont été nombreuses et variées, avec les chiffres d'abord connus écrite créés par les Egyptiens au Moyen-Uni textes comme la Papyrus Mathématique Rhind.

Chiffres mayas

Depuis les débuts de l'histoire, les principales disciplines dans les mathématiques découlaient de la nécessité de faire des calculs relatifs à la fiscalité et commerce, de comprendre les relations entre les nombres, mesurer la terre, et de prédire des événements astronomiques . Ces besoins peuvent être plus ou moins liée à la large subdivision des mathématiques dans les études sur la quantité, la structure, l'espace, et le changement.

Mathématiques a depuis été considérablement étendu, et il ya eu une interaction fructueuse entre les mathématiques et la science, au profit des deux. Découvertes mathématiques ont été faites à travers l'histoire et continuent d'être faite aujourd'hui. Selon Mikhail B. Sevryuk, dans le numéro de Janvier 2006 de la Bulletin de l'American Mathematical Society, "Le nombre de papiers et de livres inclus dans le Base de données de mathématique avis depuis 1940 (la première année de fonctionnement du MR) est maintenant plus de 1,9 millions d'habitants, et plus de 75 000 articles sont ajoutés à la base de données chaque année. L'écrasante majorité des œuvres dans cet océan contient de nouvelles mathématiques théorèmes et leurs preuves ".

Inspiration, les mathématiques pures et appliquées, et de l'esthétique

Sir Isaac Newton (1643-1727), un inventeur du calcul infinitésimal .

Mathématiques se pose partout où il ya des problèmes difficiles qui impliquent la quantité, la structure, l'espace, ou de changement. Au début, ils ont été trouvés dans commerce, la mesure de terre et plus tard l'astronomie ; de nos jours, toutes les sciences suggèrent problèmes étudiés par les mathématiciens, et de nombreux problèmes se posent dans les mathématiques elles-mêmes. Newton était l'un des inventeurs de calcul infinitésimal, même si la quasi-totalité de la notation utilisés dans calcul infinitésimal a été fourni par Leibniz à l'exception d'un point au-dessus d'une variable pour signifier la différenciation par rapport au temps. Feynman a inventé le Intégrante de chemin de Feynman en utilisant une combinaison de raisonnement et de compréhension de la physique, et aujourd'hui la théorie des cordes inspire également de nouvelles mathématiques. Certains des mathématiques ne est pertinente que dans la région qui l'a inspiré, et est appliqué pour résoudre d'autres problèmes dans ce domaine. Mais souvent, les mathématiques inspiré par une zone se avère utile dans de nombreux domaines, et rejoint la réserve générale des concepts mathématiques. Le fait remarquable que même les mathématiques "pure" se avère souvent avoir des applications pratiques est ce Eugene Wigner a appelé " la déraisonnable efficacité des mathématiques ".

Comme dans la plupart des domaines d'étude, l'explosion des connaissances dans l'ère scientifique a conduit à une spécialisation en mathématiques. Une distinction majeure entre mathématiques pures et mathématiques appliquées . Plusieurs domaines des mathématiques appliquées ont fusionné avec les traditions connexes en dehors des mathématiques et de devenir disciplines dans leur propre droit, y compris des statistiques , la recherche opérationnelle et informatique .

Pour ceux qui sont mathématiquement incliné, il ya souvent un aspect esthétique définitive à une grande partie de mathématiques. Beaucoup de mathématiciens parlent de l'élégance des mathématiques, ses intrinsèques esthétique et intérieur beauté. Simplicité et généralité sont évalués. Il ya de la beauté dans une démonstration simple et élégant, comme Euclide preuve d 'qu'il ya une infinité de nombres premiers , et dans une méthode numérique élégante qui accélère le calcul, comme le transformée de Fourier rapide. GH Hardy Apologie de mathématicien a exprimé la conviction que ces considérations esthétiques sont, en eux-mêmes, suffisants pour justifier l'étude des mathématiques pures. Les mathématiciens se efforcent souvent de trouver des preuves de théorèmes qui sont particulièrement élégante, une quête Paul Erdős souvent désigné comme trouver des preuves de "Le Livre" dans lequel Dieu avait écrit ses preuves préférés. La popularité de mathématiques récréatives est un autre signe du plaisir beaucoup trouvent dans la résolution de questions mathématiques.

Notation, la langue, et la rigueur

Le débordement symbole ∞ dans plusieurs polices de caractères.

La plupart de la notation mathématique en usage aujourd'hui n'a pas été inventé jusqu'à ce que le 16ème siècle . Avant cela, les mathématiques a été écrit en mots, un processus laborieux qui limitait découverte mathématique. Dans le 18ème siècle , Euler était responsable de la plupart des notations en usage aujourd'hui. Notation moderne rend les mathématiques beaucoup plus facile pour les professionnels, mais les débutants trouvent souvent intimidante. Il est très comprimé: quelques symboles contiennent une grande quantité d'informations. Comme la notation musicale, la notation mathématique moderne dispose d'une syntaxe stricte et encode l'information qu'il serait difficile d'écrire de toute autre manière.

Mathématique langue est également difficile pour les débutants. Des mots tels que ou et seulement avoir un sens plus précis que dans le langage courant. Confondant aussi aux débutants, des mots tels que ouvert et domaine ont été donné significations mathématiques spécialisées. Jargon mathématique comprend des termes techniques tels que homéomorphisme et intégrable. Mais il ya une raison pour la notation spéciale et le jargon technique: les mathématiques nécessite plus de précision que le langage courant. Les mathématiciens se réfèrent à cette précision du langage et de la logique «rigueur».

Rigueur est fondamentalement une question de preuve mathématique . Les mathématiciens veulent que leurs théorèmes de suivre des axiomes par des moyens de raisonnement systématique. Ce est pour éviter erronées " théorèmes », basés sur des intuitions faillibles, dont de nombreux cas se sont produits dans l'histoire de l'objet. Le niveau de rigueur prévu en mathématiques a varié au fil du temps: les Grecs devraient arguments détaillés, mais au moment de Isaac Newton les méthodes employées étaient moins rigoureux. Problèmes inhérents aux définitions utilisées par Newton conduirait à une résurgence d'une analyse minutieuse et la preuve formelle dans le 19ème siècle. Aujourd'hui, les mathématiciens continuent de soutenir entre eux sur preuves assistée par ordinateur. Depuis grands calculs sont difficiles à vérifier, ces preuves peuvent ne pas être suffisamment rigoureuses. Axiomes de la pensée traditionnelle étaient «vérités évidentes", mais que la conception est problématique. Au niveau formel, un axiome est juste une chaîne de symboles, qui a une signification intrinsèque seulement dans le contexte de l'ensemble des formules derivable d'un système axiomatique. Ce était l'objectif de Le programme de Hilbert pour mettre toutes les mathématiques sur une base axiomatique cabinet, mais selon Théorème d'incomplétude de Gödel tous les (suffisamment puissant) système axiomatique a indécidables formules; et ainsi une finale axiomatisation des mathématiques est impossible. Néanmoins mathématiques est souvent imaginé pour être (autant que son contenu formel) rien que la théorie des ensembles dans certains axiomatisation, dans le sens que tout énoncé mathématique ou de preuve pourraient être jetés dans des formules dans la théorie des ensembles.

Les mathématiques comme la science

Carl Friedrich Gauss , lui-même connu comme le «prince des mathématiciens», appelé les mathématiques comme "la reine des sciences».

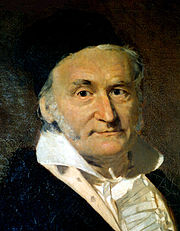
Carl Friedrich Gauss appelé mathématiques comme "la reine des sciences». Dans l'original latin Regina Scientiarum, ainsi que dans allemand Königin der Wissenschaften, le mot correspondant à des moyens scientifiques (domaine de) la connaissance. En effet, ce est aussi le sens original en anglais, et il ne fait aucun doute que les mathématiques est en ce sens une science. La spécialisation restreindre le sens à la science naturelle est de date plus tard. Si l'on considère la science comme strictement sur le monde physique, puis les mathématiques, ou au moins mathématiques pures, ne est pas une science. Albert Einstein a déclaré que «dans la mesure où les lois des mathématiques se réfèrent à la réalité, ils ne sont pas certains;. et dans la mesure où elles sont certaines, elles ne se réfèrent pas à la réalité"

Beaucoup de philosophes croient que les mathématiques ne est pas expérimentalement falsifiable, et donc pas une science, selon la définition de Karl Popper . Cependant, dans les années 1930 un travail important dans la logique mathématique a montré que les mathématiques ne peuvent pas être réduits à la logique, et Karl Popper a conclu que «la plupart des théories mathématiques sont, comme celles de la physique et de la biologie, hypothético-déductive: mathématiques pures se avère donc être beaucoup plus proche aux sciences naturelles dont hypothèses sont conjectures, qu'il ne semblait même récemment ". D'autres penseurs, notamment Imre Lakatos, ont appliqué une version de falsificationisme se mathématiques.

Un autre point de vue, ce est que certains domaines scientifiques (telles que physique théorique) sont les mathématiques avec axiomes qui sont destinés à correspondre à la réalité. En fait, le physicien théorique, JM Ziman, a proposé que la science est de notoriété publique et comprend donc les mathématiques. Dans tous les cas, les mathématiques part beaucoup en commun avec de nombreux domaines des sciences physiques, notamment l'exploration des conséquences logiques d'hypothèses. Intuition et expérimentation jouent également un rôle dans la formulation de conjectures en mathématiques et les sciences (autres). Mathématiques expérimentale continue de croître en importance au sein des mathématiques et le calcul et la simulation jouent un rôle croissant dans les deux les sciences et les mathématiques, l'affaiblissement de l'opposition que les mathématiques ne utilisent pas le méthode scientifique. Dans son livre 2002 A New Kind of Science, Stephen Wolfram fait valoir que les mathématiques de calcul mérite d'être explorée empiriquement comme un domaine scientifique à part entière.

Les opinions des mathématiciens sur cette question sont variées. Beaucoup de mathématiciens estiment que d'appeler leur région une science est de minimiser l'importance de son côté esthétique, et son histoire dans le traditionnel sept arts libéraux; d'autres estiment que d'ignorer sa connexion aux sciences est de fermer les yeux sur le fait que l'interface entre les mathématiques et ses applications dans les sciences et l'ingénierie a conduit beaucoup de développement en mathématiques. Une façon cette différence de point de vue se joue est dans le débat philosophique de savoir si les mathématiques est créé (comme dans l'art) ou découvert (comme dans la science). Il est fréquent de voir des universités divisés en sections qui comprennent une division de sciences et des mathématiques, ce qui indique que les domaines sont considérés comme étant des alliés, mais qu'ils ne coïncident pas. Dans la pratique, les mathématiciens sont généralement regroupés avec des scientifiques au niveau brut, mais séparés à des niveaux plus fins. Ce est l'une des nombreuses questions examinées dans le philosophie des mathématiques.

Récompenses mathématiques sont généralement séparés des leurs équivalents dans la science. Le prix le plus prestigieux en mathématiques est le Médaille Fields, créé en 1936 et décerné tous maintenant quatre années. Il est souvent considéré, à tort, l'équivalent de la science de Prix Nobel. Le Prix Wolf de mathématiques, institué en 1979, reconnaît les réalisations de vie, et un autre important prix international, le Prix Abel, a été introduit en 2003. Ceux-ci sont attribués pour un corps particulier de travail, qui peut être l'innovation, ou la résolution d'un problème en suspens dans un champ mis en place. Une fameuse liste de 23 ces problèmes ouverts, appelée " Problèmes de Hilbert », ont été compilées en 1900 par le mathématicien allemand David Hilbert . Cette liste a réalisé une grande célébrité parmi les mathématiciens, et au moins neuf des problèmes ont été résolus. Une nouvelle liste de sept problèmes importants, l'intitulé " Problèmes du prix du millénaire ", a été publié en 2000. Solution de chacun de ces problèmes porte une récompense de 1 million de dollars et un seul (la Hypothèse de Riemann) est dupliqué dans Problèmes de Hilbert.

Domaines des mathématiques

Un boulier , un outil simple de calcul utilisée depuis l'Antiquité

Comme indiqué plus haut, les principales disciplines dans les mathématiques premier découlaient de la nécessité de faire des calculs dans le commerce, de comprendre les relations entre les nombres, pour mesurer la terre, et de prédire astronomiques événements. Ces quatre besoins peuvent être plus ou moins liée à la large subdivision des mathématiques dans l'étude de la quantité, de la structure, de l'espace, et de changer (ce est à dire, l'arithmétique , l'algèbre , la géométrie et l'analyse ). En plus de ces principales préoccupations, il ya aussi des subdivisions dédié à l'exploration des liens du cœur des mathématiques à d'autres champs: à logique, théorie des ensembles ( fondations), aux mathématiques empiriques des différentes sciences ( mathématiques appliquées ), et plus récemment à l'étude rigoureuse de incertitude.

Quantité

L'étude de la quantité commence par un nombre premier, les familiers des nombres naturels et des nombres entiers ("nombres entiers") et les opérations arithmétiques sur eux, qui sont caractérisés en arithmétique . Les propriétés les plus profondes de entiers sont étudiés dans la théorie des nombres , où ces résultats populaires comme le dernier théorème de Fermat . La théorie des nombres détient également deux problèmes non résolus largement considérées: la conjecture des nombres premiers jumeaux et la conjecture de Goldbach .

Comme le système de numéro est développé, les entiers sont reconnus comme un sous-ensemble des nombres rationnels (« fractions »). Ceux-ci, à leur tour, sont contenues dans les nombres réels , qui sont utilisés pour représenter des quantités continues. Les nombres réels sont généralisés à des nombres complexes . Ce sont les premières étapes d'une hiérarchie des numéros qui se passe à inclure quarternions et octonions. Examen des nombres naturels conduit également à la nombres transfinis, qui formalisent le concept de comptage à l'infini. Un autre domaine d'étude est de taille, ce qui conduit à des nombres cardinaux et ensuite à une autre conception de l'infini: la numéros Aleph, qui permettent une comparaison significative de la taille d'une infinité de grands ensembles.

Nombres naturels	Entiers	Nombres rationnels	Nombres réels	Les nombres complexes

Structure

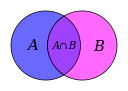
Beaucoup d'objets mathématiques, comme ensembles de nombres et fonctions , présentent la structure interne. Les propriétés structurelles de ces objets sont étudiées dans l'étude des groupes , bagues, les champs et les autres systèmes abstraits, qui sont eux-mêmes de tels objets. Ce est le domaine de l'algèbre abstraite . Un concept important ici est que des vecteurs , généralisée à espaces vectoriels , et a étudié à l'algèbre linéaire . L'étude des vecteurs combine trois des domaines fondamentaux des mathématiques:. Quantité, structure, et l'espace calcul vectoriel élargit le champ en quart domaine fondamental, celui du changement.

La théorie des nombres	Algèbre abstraite	La théorie des groupes	la théorie de la commande

Espace

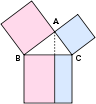
L'étude de l'espace émane de la géométrie - en particulier, la géométrie euclidienne . trigonométrie combine espace et numéros, et englobe la célèbre théorème de Pythagore . L'étude moderne de l'espace généralise ces idées à inclure la géométrie de dimension supérieure, géométries non-euclidiennes (qui jouent un rôle central dans la relativité générale ) et topologie . Quantité et l'espace jouent tous deux un rôle dans la géométrie analytique , géométrie différentielle , et géométrie algébrique. Dans la géométrie différentielle sont les concepts de faisceaux de fibres et le calcul sur les collecteurs . Dans la géométrie algébrique est la description des objets géométriques comme des ensembles de solutions de polynômes équations, combinant les notions de quantité et de l'espace, ainsi que l'étude de groupes topologiques, qui combinent la structure et de l'espace. groupes de Lie sont utilisées pour étudier l'espace, la structure, et le changement. Topologie dans toutes ses nombreuses ramifications peut-être la plus grande zone de croissance en mathématiques 20e siècle, et comprend de longue date Conjecture de Poincaré et le controversé théorème des quatre couleurs , dont la preuve que, par ordinateur, n'a jamais été vérifié par un humain.

Géométrie	Trigonométrie	Géométrie différentielle	Topologie	La géométrie fractale

Changement

Comprendre et décrire le changement est un thème commun dans le sciences naturelles, et le calcul a été développé comme un outil puissant pour faire enquête. Fonctions posent ici, comme un concept central décrivant une quantité évolution. L'étude rigoureuse des nombres réels et fonctions réelles est connu comme analyse réelle, avec analyse complexe le champ équivalent pour les nombres complexes. Le Hypothèse de Riemann, l'une des questions ouvertes les plus fondamentaux en mathématiques, est tirée de l'analyse complexe. Analyse fonctionnelle met l'accent sur (généralement de dimension infinie) des espaces de fonctions. L'une des nombreuses applications de l'analyse fonctionnelle est la mécanique quantique . Beaucoup de problèmes conduisent naturellement aux relations entre une quantité et son taux de variation, et ceux-ci sont étudiés comme des équations différentielles . De nombreux phénomènes dans la nature peuvent être décrits par systèmes dynamiques; la théorie du chaos rend précis la façon dont beaucoup de ces systèmes présentent imprévisibles mais toujours comportement déterministe.

Calcul	Calcul vectoriel	équations différentielles	Systèmes dynamiques	La théorie du chaos

Fondations et de la philosophie

Afin de clarifier la fondements des mathématiques, les champs de la logique mathématique et la théorie des ensembles ont été élaborés, ainsi que la théorie de la catégorie qui est encore en développement.

La logique mathématique est préoccupé par la mise en mathématiques sur un rigide cadre axiomatique, et d'étudier les résultats d'un tel cadre. En tant que tel, il est le foyer de Deuxième théorème d'incomplétude de Gödel, peut-être le résultat le plus largement célébré dans la logique, qui (de manière informelle) implique que toute système formel qui contient l'arithmétique de base, si le son (ce qui signifie que tous les théorèmes qui peuvent être prouvées sont vraies), est nécessairement incomplète (ce qui signifie qu'il ya de véritables théorèmes qui ne peuvent pas être prouvés dans ce système). Gödel a montré comment construire, quelle que soit la collection donnée d'axiomes la théorie des nombres, une déclaration formelle dans la logique qui est un nombre théorique fait vrai, mais qui ne suivent pas de ces axiomes. Par conséquent pas de système formel est un véritable axiomatisation de la théorie des nombres plein. La logique moderne est divisé en théorie récursivité, théorie des modèles, et la preuve la théorie, et est étroitement liée à théorique informatique .

La logique mathématique	La théorie des ensembles	La théorie des catégories

Les mathématiques discrètes

Les mathématiques discrètes est le nom commun pour les domaines des mathématiques les plus généralement utiles dans informatique théorique. Ceci comprend théorie de la calculabilité, théorie de la complexité de calcul, et théorie de l'information. théorie de la calculabilité examine les limites de différents modèles théoriques de l'ordinateur, y compris le modèle le plus puissant connue - la Machine de Turing. théorie de la complexité est l'étude de traçabilité par ordinateur; certains problèmes, bien que théoriquement résoluble par ordinateur, sont si coûteux en termes de temps ou d'espace qui leur résolution est susceptible de rester pratiquement impossible, même avec l'avance rapide du matériel informatique. Enfin, la théorie de l'information est préoccupé par la quantité de données pouvant être stockées sur un support donné, et donc des concepts tels que compression et entropie.

Comme un domaine relativement nouveau, mathématiques discrètes a un certain nombre de problèmes fondamentaux ouverts. Le plus célèbre d'entre eux est le " P = NP? "Problème, l'un des Problèmes du prix du millénaire.

Combinatoire	Théorie du calcul	Cryptographie	Théorie des graphes

Mathématiques appliquées

Mathématiques appliquées considère l'utilisation d'outils mathématiques abstraits dans la résolution de problèmes concrets dans les sciences , des affaires et d'autres domaines. Un domaine important en mathématiques appliquées est des statistiques , qui utilise la théorie des probabilités comme un outil et permet la description, l'analyse et la prévision des phénomènes où le hasard joue un rôle. La plupart des expériences, des enquêtes et des études d'observation nécessitent l'utilisation éclairée des statistiques. (Beaucoup de statisticiens, toutefois, ne se considèrent pas comme des mathématiciens, mais plutôt une partie d'un groupe allié.) Analyse numérique enquête sur les méthodes de calcul pour résoudre efficacement un large éventail de problèmes mathématiques qui sont généralement trop grand pour la capacité numérique humaine; il comprend l'étude des erreurs d'arrondi ou d'autres sources d'erreur dans les calculs.

Idées reçues

Mathématiques ne est pas un système fermé intellectuelle, dans lequel tout a déjà été élaboré. Il ne manque pas de problèmes ouverts. Mathématiciens publier des milliers de documents incorporant de nouvelles découvertes en mathématiques chaque mois.

Mathématiques ne est pas numérologie, il ne est pas la comptabilité ; ni est-il limité à l'arithmétique .

Pseudo-est une forme d'activité comme les mathématiques réalisées à l'extérieur le milieu universitaire, et parfois par les mathématiciens eux-mêmes. Il se compose souvent d'attaques sur des questions déterminées célèbres, comprenant des correcteurs tentatives faites de manière isolée (ce est-longs documents ne sont pas supportées par la théorie précédemment publiée). La relation de mathématiques généralement admis est similaire à celle entre pseudoscience et la vraie science. Les idées fausses impliqués sont normalement basés sur:

• incompréhension des implications de rigueur mathématique;
• les tentatives de contourner les critères habituels de la publication de documents mathématiques dans un revue savante après examen par les pairs, souvent dans la croyance que la revue est un parti pris contre l'auteur;
• manque de familiarité avec, et donc sous-estimation de la littérature existante.

Le cas de Le travail de Kurt Heegner montre que la création mathématique ne est ni infaillible, ni ne veulent pas admettre l'erreur dans l'évaluation du travail 'amateur'. Et comme l'astronomie , les mathématiques doit beaucoup à contributeurs amateurs comme Fermat et Mersenne.

Mathématiques et la réalité physique

Concepts et théorèmes mathématiques ne doivent pas correspondre à quelque chose dans le monde physique. Dans la mesure où il existe une correspondance, alors que les mathématiciens et les physiciens peuvent sélectionner axiomes et postulats qui semblent raisonnables et intuitive, il ne est pas nécessaire pour les hypothèses de base dans un système axiomatique pour être vrai dans un sens empirique ou physique. Ainsi, alors que beaucoup systèmes d'axiomes sont tirées de nos perceptions et expériences, ils ne sont pas à leur charge.

Par exemple, nous pourrions dire que le concept physique de deux pommes peut être précise modélisé par le nombre naturel 2. D'autre part, nous pourrions également dire que les nombres naturels ne sont pas un modèle précis, car il n'y a pas "unité" pomme standard et aucune deux pommes sont exactement semblables. L'idée de la modélisation est encore compliquée par la possibilité de fractions des pommes ou partielles. Ainsi, alors il peut être instructif de visualiser la définition axiomatique des nombres naturels comme des collections de pommes, la définition même ne dépend pas ni dérivé de toutes les entités physiques réelles.

Néanmoins, les mathématiques demeure extrêmement utile pour résoudre les problèmes du monde réel. Ce fait conduit physicien Eugene Wigner d'écrire un article intitulé " Le déraisonnable efficacité des mathématiques dans les sciences naturelles ".