
Signifier
Renseignements généraux
Ce contenu de Wikipedia a été sélectionné par SOS Enfants d'aptitude dans les écoles à travers le monde. Cliquez ici pour en savoir plus sur le parrainage d'enfants.
Dans les statistiques , la moyenne a deux significations connexes:
- la moyenne arithmétique (et se distingue de la moyenne géométrique ou moyenne harmonique).
- la valeur attendue d'une variable aléatoire , qui est aussi appelé la moyenne de population.
On dit parfois que la «moyenne» signifie moyenne. Ce est incorrect si "moyenne" est pris dans le sens spécifique de "moyenne arithmétique" comme il existe différents types de moyennes: la moyenne, la médiane et le mode . Par exemple, les prix moyens des maisons utilisent presque toujours la valeur médiane de la moyenne.
Pour une valeur réelle variable aléatoire X, la moyenne est la espérance de X. On notera que chaque pas la distribution de probabilité a une moyenne définie (ou variance ); voir le Distribution de Cauchy pour un exemple.
Pour un ensemble de données, la moyenne est la somme des observations divisé par le nombre d'observations. La moyenne est souvent cité avec l' écart-type : la moyenne décrit l'emplacement central des données, et l'écart type décrit la propagation.
Une autre mesure de la dispersion est l'écart moyen, équivalent à la moyenne déviation absolue de la moyenne. Il est moins sensible aux valeurs aberrantes, mais moins mathématiquement traitable.
Ainsi que des statistiques, des moyens sont souvent utilisés en géométrie et l'analyse; un large éventail de moyens ont été développés pour ces fins, qui ne sont pas beaucoup utilisés dans les statistiques. Ils sont énumérés ci-dessous.
Des exemples de moyens
Moyenne arithmétique
La moyenne arithmétique est la moyenne "standard", souvent simplement appelée la «moyenne».
La moyenne peut souvent être confondue avec la médiane ou le mode . La moyenne est la moyenne arithmétique d'un ensemble de valeurs, ou la distribution; cependant, pour distributions asymétriques, la moyenne ne est pas nécessairement la même que la valeur moyenne (médiane), ou (mode) le plus probable. Par exemple, le revenu moyen est biaisé vers le haut par un petit nombre de personnes avec de très gros revenus, de sorte que la majorité ont un revenu inférieur à la moyenne. En revanche, le revenu médian est le niveau auquel la moitié de la population est en dessous et la moitié est au-dessus. Le revenu de mode est le revenu le plus probable, et favorise le plus grand nombre de personnes à faible revenu. La médiane ou le mode sont souvent des mesures plus intuitives de ces données.
Cela dit, de nombreuses distributions asymétriques sont mieux décrites par leur moyenne - comme les exponentielles et Poisson distributions.
Par exemple, la moyenne arithmétique des 34, 27, 45, 55, 22, 34 (six valeurs) est (34 + 27 + 45 + 55 + 22 + 34) / 6 = 217/6 ≈ 36,167.
Moyenne géométrique
Le moyenne géométrique est une moyenne qui est utile pour les ensembles de nombres qui sont interprétées en fonction de leur produit et non pas leur somme (comme ce est le cas avec la moyenne arithmétique). Par exemple, les taux de croissance.
Par exemple, la moyenne géométrique de 34, 27, 45, 55, 22, 34 (six valeurs) est (34 × 27 × 45 × 55 × 22 × 34) 6.1 6.1 = 1699493400 = 34,545.
Moyenne harmonique
Le moyenne harmonique est une moyenne qui est utile pour des ensembles de nombres qui sont définis par rapport à certaines unité, par exemple vitesse (distance par unité de temps).
Par exemple, la moyenne harmonique des nombres 34, 27, 45, 55, 22, et 34 est
Moyen généralisé
Puissance moyenne
Le moyenne généralisée, aussi connu comme la puissance moyenne ou le titulaire dire, est une abstraction de la quadratique, l'arithmétique, géométrique et des moyens harmoniques. Elle est définie par
En choisissant la valeur appropriée pour le paramètre m nous obtenons
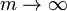 | maximum |
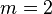 | moyenne quadratique, |
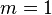 | moyenne arithmétique , |
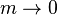 | moyenne géométrique, |
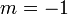 | harmonique signifie, |
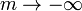 | minimum. |
f-moyen
Ceci peut être généralisé en outre que le f-généralisée moyen
et encore un choix approprié d'un inversible 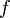 donnera
donnera
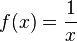 | harmonique signifie, |
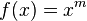 | moyen d'alimentation, |
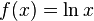 | moyenne géométrique. |
Moyenne pondérée
Le moyenne arithmétique pondérée est utilisée, si l'on veut combiner des valeurs moyennes à partir d'échantillons de la même population avec différentes tailles de l'échantillon:
Les poids 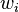 représenter les limites de l'échantillon partiel. Dans d'autres applications, ils représentent une mesure de la fiabilité de l'influence sur la moyenne de valeurs respectives.
représenter les limites de l'échantillon partiel. Dans d'autres applications, ils représentent une mesure de la fiabilité de l'influence sur la moyenne de valeurs respectives.
Moyenne tronquée
Parfois, un ensemble de nombres (la données) peut être contaminée par les valeurs aberrantes inexactes, ce est à dire des valeurs qui sont beaucoup trop bas ou trop élevé. Dans ce cas, on peut utiliser un moyenne tronquée. Il implique la suppression des parties des données fournies en haut ou l'extrémité inférieure, généralement un montant égal à chaque extrémité, puis en prenant la moyenne arithmétique des données restantes. Le nombre de valeurs retirées est indiqué en pourcentage du nombre total de valeurs.
Interquartile signifie
Le interquartile signifie, ce est un exemple concret d'une moyenne tronquée. Ce est tout simplement la moyenne arithmétique après avoir retiré le plus bas et le plus haut trimestre de valeurs.
en supposant que les valeurs ont été commandés.
Moyen d'une fonction
Dans le calcul , et surtout calcul à variables multiples, la moyenne d'une fonction est vaguement définie comme la valeur moyenne de la fonction sur sa domaine. Dans une variable, le moyen d'une fonction f (x) sur l'intervalle (a, b) est défini par
(Voir aussi valeur moyenne théorème.) Dans plusieurs variables, la moyenne sur une relativement compact domaine U dans un espace euclidien est définie par
Ceci généralise la moyenne arithmétique. D'autre part, il est également possible de généraliser la moyenne géométrique de fonctions en définissant la moyenne géométrique de f pour être
Plus généralement, théorie de la mesure et de la théorie des probabilités soit sorte de signifier joue un rôle important. Dans ce contexte, L'inégalité de Jensen place estimations pointus sur la relation entre ces deux notions différentes de la moyenne d'une fonction.
Moyenne des angles
La plupart des moyens habituels échouent sur les quantités circulaires, comme les angles , daytimes, parties fractionnaires des nombres réels . Pour les quantités que vous avez besoin d'un moyenne des quantités circulaires.
D'autres moyens
- Arithmétique-moyenne géométrique
- Arithmétique moyenne harmonique
- Lemme de Cesàro
- Moyenne Chisini
- Moyenne Contraharmonic
- Moyenne symétriques élémentaires
- Moyenne géométrique harmonique
- Heinz signifie
- Moyenne Heronian
- Identric signifierait
- Moyenne des moindres carrés
- Lehmer signifie
- Moyenne logarithmique
- Médiane
- Moyenne quadratique
- Stolarsky signifie
- Moyenne temporelle
- Moyenne géométrique pondérée
- Moyenne harmonique pondérée
- L'entropie de Rényi (un généralisée f-moyen)
Propriétés
La méthode la plus générale pour définir une moyenne ou moyenne, y, prend toute fonction d'une liste g (x_1, x_2, ..., xn), qui est symétrique par permutation des membres de la liste, et l'assimile à la même fonction de la valeur de la moyenne remplacement de chaque membre de la liste: g (x 1, x_2, ..., xn) = g (y, y, ..., y). Tous les moyens part certaines propriétés et d'autres propriétés sont partagées par les moyens les plus courants. Certaines de ces propriétés sont collectés ici.
Moyenne pondérée
Une moyenne pondérée 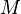 est une fonction qui associe uplets de nombres positifs à un nombre positif (
est une fonction qui associe uplets de nombres positifs à un nombre positif ( 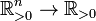 ).
).
- " Point fixe ":
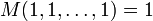
- Homogénéité:
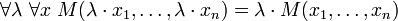
- (En utilisant notation vectorielle:
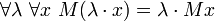 )
)
- (En utilisant notation vectorielle:
- Monotonie:
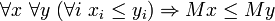
Cela suit
- Borné:
![\ Forall x \ M x \ in [\ x min, \ max x]](../../images/135/13510.png)
- Continuité:
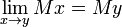
- Croquis d'une preuve: Parce que
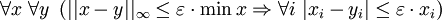 et
et 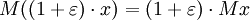 cela suit
cela suit 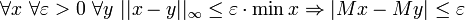 .
.
- Il existe des moyens qui ne sont pas dérivables . Par exemple, le nombre maximal d'un tuple est considérée comme un moyen (comme un cas extrême de la puissance moyenne, ou comme un cas particulier d'une médiane ), mais ne est pas différentiable.
- Tous les moyens énumérés ci-dessus, à l'exception de la majeure partie de la F-moyen généralisé, satisfont les propriétés présentées.
- Si
 est bijective, le f-moyenne généralisée satisfait la propriété de point fixe.
est bijective, le f-moyenne généralisée satisfait la propriété de point fixe. - Si
 est strictement monotone, le f-moyenne généralisée satisfaire également la propriété de monotonie.
est strictement monotone, le f-moyenne généralisée satisfaire également la propriété de monotonie. - En général, un f-moyenne généralisée ratera homogénéité.
- Si
Les propriétés ci-dessus impliquent des techniques pour construire des moyens plus complexes:
Si  des moyens pondérés,
des moyens pondérés, 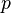 est un facteur positif nombre réel , alors
est un facteur positif nombre réel , alors 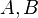 avec
avec
sont également une moyenne pondérée.
Moyenne non pondérée
Intuitivement parlé, moyenne non pondérée est une moyenne pondérée avec des poids égaux. Depuis notre définition de la moyenne pondérée ci-dessus ne expose pas des poids particulières, des poids égaux doivent être maintenus par un autre chemin. Un point de vue différent sur la pondération est homogène, que les entrées peuvent être échangés sans altérer le résultat.
Ainsi nous définissons 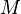 étant une moyenne non pondérée se il se agit d'une moyenne pondérée, et pour chaque permutation
étant une moyenne non pondérée se il se agit d'une moyenne pondérée, et pour chaque permutation 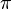 des entrées, le résultat est le même. Laisser
des entrées, le résultat est le même. Laisser 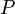 comme l'ensemble des permutations de
comme l'ensemble des permutations de 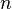 -uplets.
-uplets.
- Symétrie:
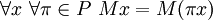
De manière analogue aux moyens pondérés, si 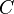 est une moyenne pondérée et
est une moyenne pondérée et 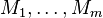 sont des moyens non pondérés,
sont des moyens non pondérés, 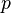 est un facteur positif nombre réel , alors
est un facteur positif nombre réel , alors 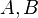 avec
avec
sont également des moyens non pondérés.
Convertir moyenne non pondérée à moyenne pondérée
Une moyenne non pondérée peut être transformé en une moyenne pondérée par des éléments répéter. Cette connexion peut également être utilisé pour indiquer qu'une moyenne est la version pondérée d'une moyenne non pondérée. Disons que vous avez la moyenne non pondérée 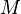 et le poids des chiffres par des nombres naturels
et le poids des chiffres par des nombres naturels 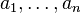 . (Si les chiffres sont rationnelle , puis les multiplier avec le dénominateur commun moins). Puis la moyenne pondérée correspondante
. (Si les chiffres sont rationnelle , puis les multiplier avec le dénominateur commun moins). Puis la moyenne pondérée correspondante 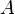 est obtenu par
est obtenu par
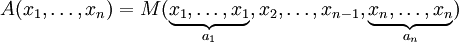 .
.
Moyens de tuples de différentes tailles
Si un moyen 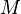 est défini pour plusieurs tuples de taille, alors on se attend également que la moyenne d'un tuple est délimitée par le moyen de cloisons. Plus précisément
est défini pour plusieurs tuples de taille, alors on se attend également que la moyenne d'un tuple est délimitée par le moyen de cloisons. Plus précisément
- Compte tenu d'un tuple arbitraire
 , Qui est partitionné en
, Qui est partitionné en 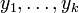 , Alors il détient
, Alors il détient 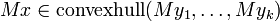 . (Voir Enveloppe convexe)
. (Voir Enveloppe convexe)
L'enseignement des mathématiques
Dans de nombreuses normes de l'Etat et programmes du gouvernement, les élèves sont censés traditionnellement à apprendre ni le sens ni la formule de calcul de la moyenne par la quatrième année. Cependant, dans de nombreux programmes de mathématiques basée sur les standards, les étudiants sont encouragés à inventer leurs propres méthodes, et ne peuvent être enseignées la méthode traditionnelle. textes de réforme de base tels que TERC en fait décourager l'enseignement de la traditionnelle "ajouter les numéros et diviser par le nombre d'éléments" méthode en faveur de passer plus de temps sur le concept de la médiane , qui ne nécessite pas la division. Cependant, la moyenne peut être calculée avec une calculatrice à quatre fonctions simple, tandis que la médiane nécessite un ordinateur. Le même guide de l'enseignant consacre plusieurs pages sur la façon de trouver la médiane d'un ensemble, qui est jugée plus simple que de trouver la moyenne.

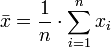
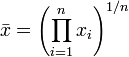
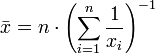
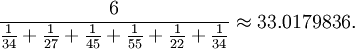
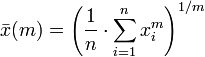
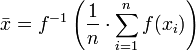
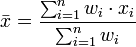
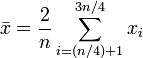
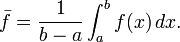
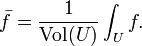
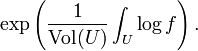
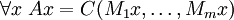
![\ Forall x \ B x = \ sqrt [p] {C (x_1 ^ p, \ dots, x_n ^ p)}](../../images/135/13518.png)
![\ Forall x \ B x = \ sqrt [p] {M_1 (x_1 ^ p, \ dots, x_n ^ p)}](../../images/135/13521.png)
