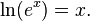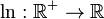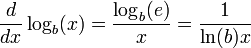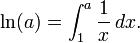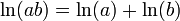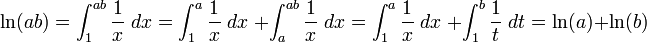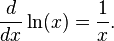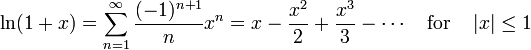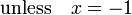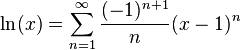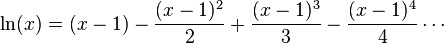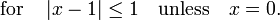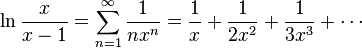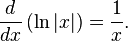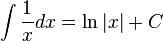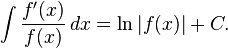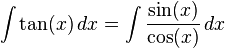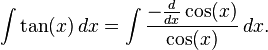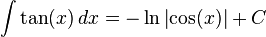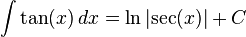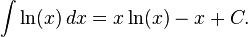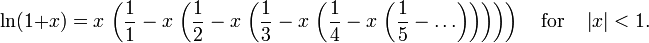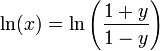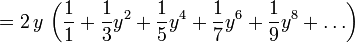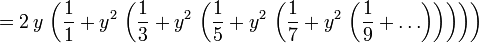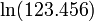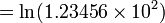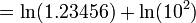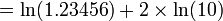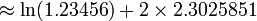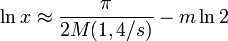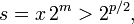Logarithme naturel

À propos de ce écoles sélection Wikipedia

Enfants SOS ont produit une sélection d'articles de wikipedia pour les écoles depuis 2005. Cliquez ici pour plus d'informations sur les enfants SOS.

Le logarithme naturel, anciennement connu sous le nom logarithme hyperbolique, est le logarithme de la base e, où e est un irrationnel constante approximativement égale à 2,718 281 828 459. En termes simples, le logarithme naturel d'un nombre x est la puissance à laquelle e devrait être soulevée à l'égalité x - par exemple le logarithme naturel de e lui-même est une cause e ¹ = e, tandis que le logarithme naturel de 1 serait 0, puisque e ⁰ = 1. Le logarithme naturel peut être défini pour tous les positifs nombres réels x que l' aire sous la courbe y = 1 / t de 1 à x, et peut également être défini pour zéro non nombres complexes comme expliqué ci-dessous .

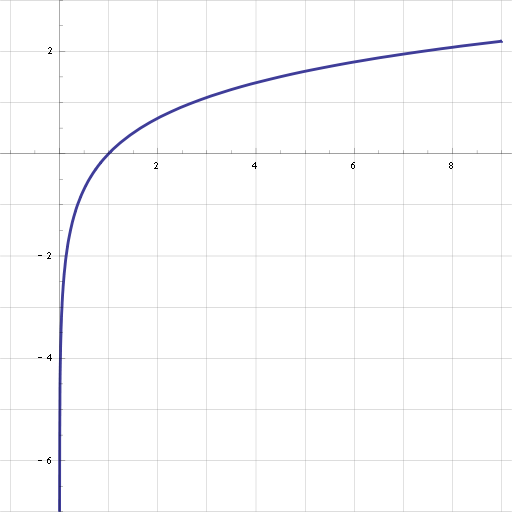
Le graphique de la fonction de logarithme naturel. La fonction va vite à l'infini négative lorsque x tend vers 0, mais se développe lentement à l'infini positif x augmente.

La fonction de logarithme naturel peut également être définie comme étant la fonction inverse de la fonction exponentielle , ce qui conduit à l'identité:

$e ^ {\ ln (x) = x} \ qquad \ mbox {} si x> 0 \, \!$

$\ Ln (e ^ x) = x. \, \!$

En d'autres termes, la fonction logarithme est une bijection de l'ensemble des nombres réels positifs à l'ensemble des nombres réels. Il est plus précisément une isomorphisme du groupe des nombres réels positifs sous la multiplication au groupe des nombres réels en vertu de plus. Représenté en fonction :

$\ Ln: \ mathbb {R} ^ + \ à \ mathbb {R}$

Les logarithmes peuvent être définis pour ne importe quelle base positif autre que 1, et pas seulement e, et sont utiles pour la résolution d'équations dont l'inconnue apparaît comme l'exposant d'une autre quantité.

Conventions de notation

Mathématiciens, statisticiens, et quelques ingénieurs comprennent généralement soit "log (x)» ou «ln (x)» signifie log _e (x), ce est à dire, le logarithme naturel de x, et écrire «log ₁₀ (x)" si le logarithme en base 10 de x est destiné.

Certains ingénieurs, biologistes, et quelques autres écrivent généralement "ln (x)" (ou parfois "log _e (x)") quand ils veulent dire le logarithme naturel de x, et prennent "log (x)» signifie log ₁₀ (x) ou, dans le cas de certains des informaticiens , log ₂ (x) (lg bien que ce est souvent écrit (x) à la place).

En plus couramment utilisés langages de programmation , y compris C , C ++ , MATLAB, Fortran, et BASE , "log" ou "log" se réfère au logarithme naturel.

Dans portatifs calculatrices , le logarithme naturel est notée ln, alors journal est le logarithme en base 10.

Pourquoi il est appelé «naturel»

Initialement, il pourrait sembler que, depuis notre système de numérotation est base 10 , cette base serait plus «naturel» que la base e. Mais mathématiquement, le nombre 10 ne est pas particulièrement importante. Son utilisation culturellement comme base pour de nombreuses sociétés de numérotation des systèmes susceptibles découle de l'homme de nombre typique de doigts. Et d'autres cultures ont basé leur système de comptage sur ces choix comme 5, 20, et 60.

Log _E est un journal «naturel» parce qu'il vient automatiquement à partir, et semble si souvent, en mathématiques. Par exemple, considérons le problème de différencier une fonction logarithmique:

$\ Frac {d} {dx} \ log_b (x) = \ frac {\ log_b (e)} {x} = \ frac {1} {\ ln (b) x}$

Si le e est égal à base b, puis le dérivé est simplement 1 / x, et x = 1 ce dérivé est égal à 1. Un autre sens dans lequel le logarithme base-e est la plus naturelle, ce est qu'il est possible de définir très facilement en termes de simple intégrante ou série de Taylor et ce ne est pas vrai pour d'autres logarithmes.

D'autres sens de ce naturel ne font aucune utilisation du calcul. A titre d'exemple, il ya un certain nombre de séries simples impliquant le logarithme naturel. En fait, Pietro et Mengoli Nicholas Mercator appelé Logarithmus naturalis quelques décennies avant que Newton et Leibniz développés calcul.

Définitions

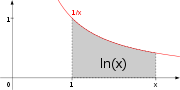
Ln (x) définie comme l'aire sous la courbe f (x) = 1 / x.

Formellement, ln (a) peut être définie comme étant la surface sous le graphique de 1 / x allant de 1 à a, ce est que l' intégrale ,

$\ Ln (a) = \ int_1 ^ a \ frac {1} {x} \, dx.$

Ceci définit un logarithme parce qu'elle satisfait la propriété fondamentale d'un logarithme:

$\ Ln (ab) = \ ln (a) + \ ln (b) \, \!$

Ceci peut être démontré en laissant 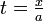$t = \ frac xa$ comme suit:

$\ Ln (ab) = \ int_1 ^ {ab} \ frac {1} {x} \; dx = \ int_1 ^ a \ frac {1} {x} \; dx \; + \ Int_a ^ {ab} \ frac {1} {x} \; dx = \ int_1 ^ {a} \ frac {1} {x} \; dx \; + \ Int_1 ^ {b} \ frac {1} {t} \; dt = \ ln (a) + \ ln (b)$

Le numéro e peut alors être défini comme le nombre réel unique, telle que ln (a) = 1.

Alternativement, si le fonction exponentielle a été définie en utilisant d'abord un série infinie, le logarithme naturel peut être définie comme la fonction inverse , ce est-ln (x) est que la fonction de telle sorte que 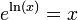$e ^ {\ ln (x) = x} \!$ . Depuis la plage de la fonction exponentielle sur des arguments réels est tous les nombres réels positifs et depuis la fonction exponentielle est strictement croissante, ce est bien définie pour tout x positif.

Dérivée, série de Taylor

Le dérivé du logarithme naturel est donnée par

$\ Frac {d} {dx} \ ln (x) = \ frac {1} {x}. \,$

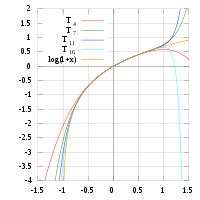
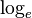Les polynômes de Taylor pour $\ Log_e$ (1 + x) ne prévoient que des approximations précises dans la plage -1 <x ≤ 1. Notez que, pour x> 1, les polynômes de Taylor de degré supérieur sont des approximations pire.

Cela conduit à la série de Taylor pour 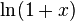$\ Ln (1 + x)$ autour 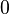$0$ ; également connu sous le nom Série Mercator

$\ Ln (1 + x) = \ sum_ {n = 1} ^ \ infty \ frac {(- 1) ^ {n + 1}} {n} x ^ n = x - \ frac {x ^ 2} {2 } + \ frac {x ^ 3} {3} - \ cdots \ quad {\ rm for} \ quad \ left | x \ right | \ leq 1 \ quad$

${\ Rm moins} \ quad x = -1$

A droite, une photo de 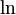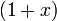$\ Ln$ $(1 + x)$ et une partie de son polynômes de Taylor autour 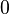$0$ . Ces approximations convergent à la fonction que dans la région -1 <x ≤ 1; en dehors de cette région la plus élevée degré polynômes de Taylor sont des approximations pire pour la fonction.

En substituant x -1 pour x, nous obtenons une forme alternative pour ln (x) lui-même, à savoir

$\ Ln (x) = \ sum_ {n = 1} ^ \ infty \ frac {(- 1) ^ {n + 1}} {n} (x-1) ^ n$

$\ Ln (x) = (x - 1) - \ frac {(x-1) ^ 2} {2} + \ frac {(x-1) ^ 3} {3} - \ frac {(x-1) ^ 4} {4} \ cdots$

${\ Rm for} \ quad \ left | x-1 \ right | \ leq 1 \ quad {\ rm moins} \ quad x = 0.$

En utilisant le Euler transformée de la série Mercator, on obtient ce qui suit, qui est valable pour tout x ayant une valeur absolue supérieure à 1:

$\ Ln {x \ x {plus-1}} = \ sum_ {n = 1} ^ \ infty {1 \ over {nx ^ n}} = {1 \ over x} + {1 \ over {2x} ^ 2 } + {1 \ over {3x ^ 3}} + \ cdots$

Cette série est similaire à un BBP type formule.

Notez également que 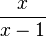$x \ x {plus-1}$ est sa propre fonction inverse, de sorte que pour obtenir le logarithme naturel d'un certain nombre n, il suffit de mettre en 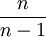$n \ over {n-1}$ pour x.

Le logarithme naturel de l'intégration

Le logarithme naturel permet simple, l'intégration des fonctions de la forme g (x) = f '(x) / f (x): un primitive de g (x) est donnée par ln (| f (x) |). Ce est le cas en raison de la règle de la chaîne et le fait suivant:

$\ {D \ over dx} \ left (\ ln \ left | x \ right | \ right) = {1 \ over x}.$

Autrement dit,

$\ Int {1 \ over x} dx = \ ln | x | + C$

$\ Int {\ frac {f '(x)} {f (x)} \, dx} = \ ln | f (x) | + C.$

Voici un exemple dans le cas de g (x) = tan (x):

$\ Int \ tan (x) \, dx = \ int {\ sin (x) \ over \ cos (x)} \, dx$

$\ Int \ tan (x) \, dx = \ int {- {d \ over dx} \ cos (x) \ over {\ cos (x)}} \, dx.$

Laisser f (x) = cos (x) et f '(x) = - sin (x):

$\ Int \ tan (x) \, dx = - \ ln {\ left | \ cos (x) \ right |} + C$

$\ Int \ tan (x) \, dx = \ ln {\ left | \ s (x) \ right |} + C$

où C est une constante arbitraire d'intégration.

Le logarithme naturel peut être intégré à l'aide intégration par parties:

$\ Int \ ln (x) \, dx = x \ ln (x) - x + C.$

Valeur numérique

Pour calculer la valeur numérique du logarithme naturel d'un nombre, l'expansion en série de Taylor peut être réécrite comme:

$\ ln (1 + x) = x \, \ left (\ frac {1} {1} - x \, \ left (\ frac {1} {2} - x \, \ left (\ frac {1} { 3} - x \, \ left (\ frac {1} {4} - x \, \ left (\ frac {1} {5} - \ ldots \ right) \ right) \ right) \ right) \ right) \ quad {\ rm for} \ quad \ left | x \ right | <1 \, \.!$

Pour obtenir un meilleur taux de convergence, l'identité suivante peut être utilisée.

$\ Ln (x) = \ ln \ left (\ frac {1} {+ y 1-y} \ right)$	$= 2 \, y \, \ left (\ frac {1} {1} + \ frac {1} {3} y ^ {2} + \ frac {1} {5} y ^ {4} + \ frac { 1} {7} y ^ {6} + \ frac {1} {9} y ^ {8} + \ ldots \ right)$
	$= 2 \, y \, \ left (\ frac {1} {1} + y ^ {2} \, \ left (\ frac {1} {3} + y ^ {2} \, \ left (\ frac {1} {5} + y ^ {2} \, \ left (\ frac {1} {7} + y ^ {2} \, \ left (\ frac {1} {9} + \ ldots \ right) \ right) \ right) \ right) \ right)$

à condition que y = (x-1) / (x + 1) et x> 0.

Pour ln (x) où x> 1, plus la valeur de x est de 1, plus la vitesse de convergence. Les identités associées avec le logarithme peuvent être mis à profit pour exploiter cette:

$\ Ln (123,456) \!$	$= \ Ln (1,23456 \ times 10 ^ 2) \, \!$
	$= \ Ln (1,23456) + \ ln (10 ^ 2) \, \!$
	$= \ Ln (1,23456) + 2 \ times \ ln (10) \, \!$
	$\ env \ ln (1,23456) + 2 \ times 2,3025851 \, \!$

Ces techniques ont été utilisées avant calculatrices, en se référant aux tables numériques et d'effectuer des manipulations comme celles ci-dessus.

Haute précision

Pour calculer le logarithme naturel avec de nombreux chiffres de précision, l'approche en série de Taylor ne est pas efficace car la convergence est lente. Une alternative est d'utiliser la méthode de Newton pour inverser la fonction exponentielle, dont la série converge plus rapidement.

Une alternative pour le calcul de très haute précision est la formule

$\ Ln x \ approx \ frac {\ pi} {2 M (1,4 / s)} - m \ ln 2$

où M désigne le arithmétique et la moyenne géométrique et

$s = x \, 2 ^ m> 2 ^ {p / 2},$

avec m choisi de sorte que P bits de précision est atteint. En effet, si cette méthode est utilisée, Newton inversion du logarithme naturel peut inversement être utilisée pour calculer la fonction exponentielle de manière efficace. (Les constantes ln 2 et π peuvent être pré-calculés à la précision souhaitée à l'aide de ne importe quel connu plusieurs séries convergent rapidement).

Complexité de calcul

Le complexité de calcul consistant à calculer le logarithme naturel (en utilisant la moyenne arithmétique-géométrique) est O (M (n) ln n). Ici, n est le nombre de chiffres de précision à laquelle le logarithme naturel doit être évaluée et M (n) est la complexité de calcul de la multiplication de deux nombres à chiffres n.

Logarithmes complexes

La fonction exponentielle peut être étendue à une fonction qui donne un nombre complexe ^x e comme pour tout nombre complexe x arbitraire; il suffit d'utiliser la série infinie avec x complexe. Cette fonction exponentielle peut être inversée pour former un logarithme complexe qui présente de plus des propriétés du logarithme ordinaire. Il ya deux difficultés: pas a x e ^x = 0; et il se avère que e ^{2 πi} = 1 ⁰ = e. Depuis la propriété multiplicatif travaille toujours pour la fonction exponentielle complexe, e ^z = ^{z 2} e ^nπi, pour tout z complexe et entiers n.

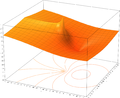
Donc le logarithme ne peut pas être défini pour toute la plan complexe , et même alors, il est multi-valeurs - tout logarithme complexe peut être modifié dans un logarithme «équivalent» en ajoutant un multiple entier de deux πi à volonté. Le logarithme complexe ne peut être à valeur unique sur le plan de coupe . Par exemple, ln i = 1/2 ou 5/2 πi πi ou -3/2 πi, etc .; et bien que je ⁴ = 1, 4 log i peut être définie comme deux πi, ou 10 πi ou -6 πi, et ainsi de suite.

Parcelles de la fonction logarithme naturel sur le plan complexe (branche principale)
z = Re (ln (x + iy))
z = | Im (ln (x + iy)) |
z = | ln (x + iy) |
La superposition des trois graphes précédents

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Natural_logarithm&oldid=206770613 "

We provide Linux to the World