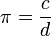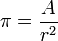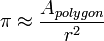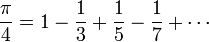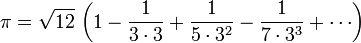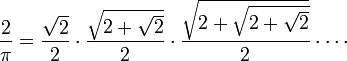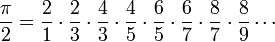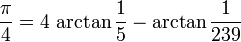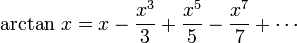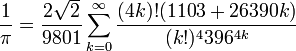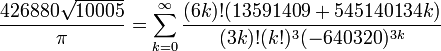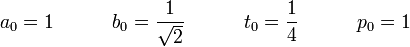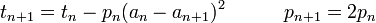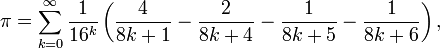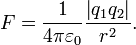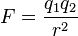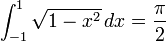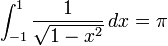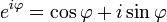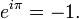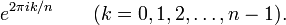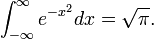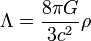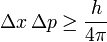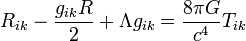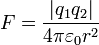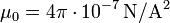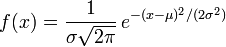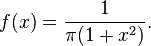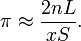Pi

Lorsque le diamètre d'un cercle est 1, sa circonférence est π.

Liste des numéros - Les nombres irrationnels ζ (3) - √2 - √3 - √5 - φ - α - e - π - δ
Binaire	11,00100100001111110110 ...
Décimal	3,14159265358979323846 ...
Hexadécimal	3.243F6A8885A308D31319 ...
Fraction continue	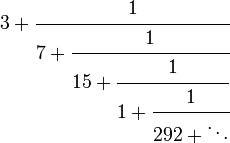Notez que cette fraction continue ne est pas périodique.

Pi ou π est une des plus importantes constantes mathématiques, à peu près égales à 3,14159. Il représente le rapport de tout cercle circonférence de son diamètre en géométrie euclidienne , qui est le même que le rapport de la superficie d'un cercle au carré de son rayon. Beaucoup de formules des mathématiques, la science et l'ingénierie impliquent π.

Ce est un nombre irrationnel , ce qui signifie qu'il ne peut pas être exprimée comme une fraction m / n, où m et n sont des nombres entiers . Par conséquent son représentation décimale ne finit jamais ou des répétitions. En plus d'être irrationnel , ce est un nombre transcendant, ce qui signifie qu'aucun ordre fini des opérations algébriques sur les nombres entiers (puissances, de racines, sommes, etc.) ne pourrait jamais produire. Tout au long de l'histoire des mathématiques, beaucoup d'efforts ont été faits pour π déterminer plus précisément et de comprendre sa nature; la fascination avec le nombre a même reporté dans la culture au sens large.

La lettre π grec, souvent défini pi en texte, a été adopté pour le nombre du mot grec pour le périmètre "περίμετρος", probablement par William Jones en 1706, et popularisé par Leonhard Euler quelques années plus tard. La constante est parfois aussi appelée la constante circulaire, d'Archimède 'constante (à ne pas confondre avec un Nombre d'Archimède), ou Le numéro de Ludolph.

Fundamentals

La lettre π

Minuscule π (la lettre minuscule est utilisé pour la constante)

Le nom de la Lettre grecque π est pi, et cette orthographe est utilisée dans contextes typographiques où la lettre grecque ne est pas disponible ou lorsque son utilisation pourrait être problématique. Lorsqu'on se réfère à cette constante, le symbole π est toujours prononcé comme "tarte" en anglais , la prononciation anglaise conventionnelle de la lettre. En grec, le nom de cette lettre est prononcé / pi /.

Le constante est appelée "π" parce que "π" est la première lettre des grecs mots περιφέρεια (périphérie) et περίμετρος (périmètre), probablement à son utilisation dans la formule de trouver la circonférence, ou le périmètre d'un cercle. π est Unicode caractère U + 03C0 (" minuscule grecque pi ").

Définition

Circonférence = π × diamètre

En géométrie plane euclidienne , π est définie comme la rapport d'un cercle de l ' sa circonférence au diamètre :

A noter que le rapport ^c / _d ne dépend pas de la taille du cercle. Par exemple, si un cercle a deux fois le diamètre d de l'autre cercle, il aura également deux fois la circonférence c, en conservant le rapport ^c / _d. Cet effet est une conséquence de la similitude de tous les milieux.

Aire du cercle = π × superficie de la place ombragée

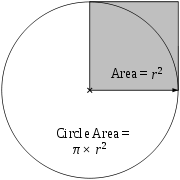
Alternativement π peut être également défini comme le rapport d'un cercle de la zone (A) à la zone d'un carré dont le côté est égal à la rayon:

La constante π peut être définie par d'autres moyens qui permettent d'éviter les concepts de longueur de l'arc et de la zone, par exemple, que deux fois par le plus petit x positif pour ce qui cos (x) = 0. Les formules ci-dessous illustrent d'autres définitions (équivalentes).

Irrationalité et de la transcendance

La constante π est un nombre irrationnel ; autrement dit, il ne peut pas être écrit par le rapport de deux nombres entiers . Cela a été prouvé dans 1761 par Johann Heinrich Lambert. Au 20e siècle, les preuves ont été trouvées qui exigent aucune connaissance préalable delà calcul intégral. Un de ceux, en raison de Ivan Niven, est largement connu. Une preuve un peu plus tôt similaire est par Mary Cartwright.

En outre, π est également transcendantale, comme cela a été prouvé par Ferdinand von Lindemann en 1882 . Cela signifie qu'il n'y a pas polynôme avec rationnels de coefficients qui est un π racine. Une conséquence importante de la transcendance de π est le fait que ce ne est pas constructible. Parce que les coordonnées de tous les points qui peuvent être construits avec règle et au compas sont des nombres constructibles, il est impossible de la quadrature du cercle: ce est, il est impossible de construire, en utilisant règle et au compas seul, un carré dont la superficie est égale à la surface d'un cercle donné.

Valeur numérique

La valeur numérique de π tronquée à 50 décimales est:

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510

Voir les liens ci-dessous et ceux de la séquence A000796 dans OEIS pour plus de chiffres.

Bien que la valeur de pi a été calculé à plus d'un billions (10 ¹²⁾ chiffres, applications élémentaires, tels que le calcul de la circonférence d'un cercle, aura rarement besoin de plus d'une douzaine de décimales. Par exemple, une valeur tronquée à 39 décimales est suffisant pour calculer la circonférence de ne importe quel cercle qui se adapte dans le univers observable avec une précision comparable à la taille d'un atome d'hydrogène.

π lui-même a une infinie développement décimal; parce π est un nombre irrationnel , son expansion décimale ne finit jamais et ne répéter. Cette séquence infinie de chiffres a mathématiciens et laïcs fasciné aussi bien, et beaucoup d'efforts au cours des derniers siècles a été mis en calcul plusieurs chiffres et d'enquêter sur les propriétés du nombre. Malgré beaucoup de travail analytique et calculs de superordinateurs qui ont déterminé plus de 1 billion chiffres de π, aucun modèle simple dans les chiffres ne ont jamais été trouvés. Chiffres de π sont disponibles sur de nombreuses pages web, et il est logiciel de calcul π à des milliards de chiffres sur ne importe quel ordinateur personnel .

Π calcul

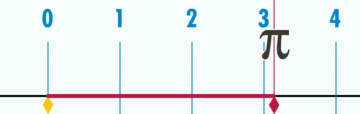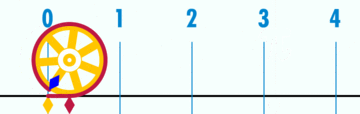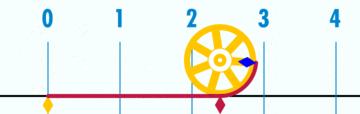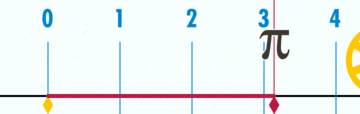
π peut être mesurée de façon empirique en dessinant un grand cercle, puis en mesurant le diamètre et la circonférence, depuis la circonférence d'un cercle est toujours π fois son diamètre. Une autre approche basée sur la géométrie, en raison de Archimedes , est d'attirer un cercle imaginaire de rayon r centré à l'origine. L'aire du cercle peut être approximée par l'inscription d'un polygone régulier à l'intérieur du cercle, et le calcul de la superficie du polygone; les plus côtés du polygone a, plus l'approximation. Puis, en utilisant la relation que la zone A d'un cercle est π fois le carré du rayon r, π peut être approchée en utilisant:

π peut également être calculé en utilisant des méthodes purement mathématiques. La plupart des formules utilisées pour calculer la valeur de π ont des propriétés mathématiques souhaitables, mais sont difficiles à comprendre sans un fond dans la trigonométrie et le calcul . Cependant, certains sont assez simples, comme cette forme de la Série Leibniz:

.

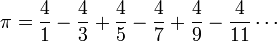Bien que cette série est facile à écrire et à calculer, il ne est pas immédiatement évident pourquoi il donne π. En outre, cette série converge si lentement que 300 termes ne sont pas suffisantes pour calculer correctement π à 2 décimales.

Histoire

L'histoire de π parallèle le développement des mathématiques dans son ensemble. Certains auteurs divisent les progrès en trois périodes: la période antique au cours de laquelle a été étudiée π géométriquement, l'époque classique la suite du développement du calcul en Europe autour du 17ème siècle, et l'âge des ordinateurs numériques.

Période géométrique

Que le rapport de la circonférence au diamètre d'un cercle est le même pour tous les milieux, et qu'il est un peu plus de trois, était connu pour géomètres égyptienne, babylonienne, indiens et grecs anciens. Les approximations connus les plus anciens datent de 1900 autour de Colombie-Britannique; ils sont 25/8 (Babylone) et 256/81 (Egypte), à la fois au sein de 1% de la valeur réelle. Le texte indien Shatapatha Brahmane donne π ≈ 339/108 que 3,139. Le Tanakh semble suggérer, dans le livre de Kings, que π = 3, qui est notamment pire que les autres estimations disponibles au moment de la rédaction (600 avant JC). L'interprétation du passage est contestée, comme certains le croient le rapport de 3: 1. Est d'une circonférence extérieure d'un diamètre intérieur d'un bassin à paroi mince, ce qui pourrait bien être un rapport précis, en fonction de l'épaisseur des murs Voir: Valeur biblique de Pi.

Archimède (287-212 avant JC) fut le premier à π estimer rigoureusement. Il a réalisé que son ampleur peut être limitée par le dessous et ci-dessus en inscrivant cercles polygones réguliers et calculer les périmètres respectifs des polygones extérieurs et intérieurs de:

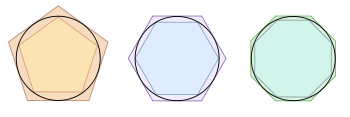
En utilisant l'équivalent de 96 polygones-verso, il a prouvé que 223/71 <π <22/7. Prenant la moyenne de ces valeurs donne 3,1419. Dans les siècles suivants, la plupart développement important a eu lieu en Inde et en Chine. Autour de 480, le mathématicien chinois Zu Chongzhi donné le rapprochement π = 355/113, et a montré que 3,1415926 <π <3,1415927, qui se présenter comme la valeur la plus précise pour π au cours des 900 prochaines années.

Période classique

Jusqu'à ce que le deuxième millénaire, π était connu à moins de 10 chiffres décimaux. La prochaine avancée majeure dans l'étude de π est venu avec le développement de calcul , et en particulier la découverte de série infinie qui, en principe permis calcul π à toute précision souhaitée en ajoutant suffisamment nombreux termes. Autour de 1400, Madhava de Sangamagrama trouvé le premier connu une telle série:

(Maintenant connu sous le nom Série Leibniz depuis qu'il a été redécouvert par James Gregory et Gottfried Leibniz au 17e siècle). Malheureusement, le taux de convergence est trop lent pour calculer le nombre de chiffres dans la pratique; environ 4000 termes doivent être additionnées pour améliorer l'estimation d'Archimède. Cependant, en transformant dans la série

Madhava a pu calculer que π 3,14159265359, correct de 11 décimales. Le record a été battu en 1424 par l'astronome persan Al-Kachi, qui a déterminé 16 décimales de π.

La première contribution européenne majeure depuis Archimède a été faite par le mathématicien allemand Ludolph van Ceulen (1540-1610), qui a utilisé une méthode géométrique pour calculer 35 décimales de π. Il était si fier de calcul, qui exigeait la plus grande partie de sa vie, qu'il avait les chiffres gravés dans sa pierre tombale.

Vers la même époque, les méthodes de calcul et la détermination de la série et des produits pour les quantités géométriques infinie ont commencé à émerger en Europe. La première représentation a été la La formule de Viète,

trouvée par François Viète en 1593. Un autre résultat est célèbre Le produit de Wallis,

écrit par . John Wallis en 1655 Isaac Newton lui-même dérivé d'une série de π et calculées 15 chiffres, mais il a avoué plus tard: «Je ai honte de vous dire de combien de chiffres que je portais ces calculs, ne ayant d'autre entreprise à l'époque."

John Machin était le premier à calculer 100 décimales de π, en utilisant la formule

avec

Formules de ce type, maintenant connu sous le nom Formules de Machin, ont été utilisés pour définir plusieurs enregistrements successifs et sont restés la meilleure méthode connue pour calculer π bien dans l'ère des ordinateurs. Un bilan remarquable a été fixé par le prodige de calcul Zacharias Dase, qui en 1844 employait une Formule de Machin pour calculer 200 décimales de π dans sa tête. La meilleure valeur à la fin du 19ème siècle était due à William Shanks, qui a pris 15 années pour calculer π avec 707 chiffres, bien qu'en raison d'une erreur que la première 527 était correcte. (Pour éviter de telles erreurs, modernes calculs de disques de toute nature sont souvent effectuées deux fois, avec deux formules différentes. Si les résultats sont les mêmes, ils sont susceptibles d'être correcte.)

Avancées théoriques dans le 18ème siècle ont conduit à des idées sur la nature de π qui ne pourraient pas être obtenus grâce à un calcul numérique seul. Johann Heinrich Lambert prouva l'irrationalité de π en 1761, et Adrien-Marie Legendre se est avéré en 1794 que π ² est aussi irrationnel. Lorsque Leonhard Euler en 1735 résolu la célèbre Problème de Bâle - trouver la valeur exacte de

qui est π ^2/6, il a établi un lien profond entre π et nombres premiers . Les deux Legendre et Leonhard Euler spéculé que π pourrait être transcendantale, un fait qui a été prouvé en 1882 par Ferdinand von Lindemann.

Livre une nouvelle introduction de William Jones mathématiques de 1706 est cité comme le premier texte où le Lettre grecque π a été utilisé pour cette constante, mais cette notation est devenue particulièrement populaire après Leonhard Euler adopté en 1737. Il a écrit:

Calcul de l'âge de l'ordinateur

L'avènement des ordinateurs numériques au 20ème siècle a conduit à une augmentation du taux de nouveaux records de calcul π. John von Neumann utilisé ENIAC pour calculer 2037 chiffres de π en 1949, un calcul qui a pris 70 heures. Des milliers de décimales supplémentaires ont été obtenus dans les décennies suivantes, avec le cap du million chiffres adoptée en 1973. Les progrès ne était pas seulement due à un matériel plus rapide, mais aussi de nouveaux algorithmes. Un des développements les plus significatifs a été la découverte de la transformée de Fourier rapide (FFT) dans les années 1960, qui permet à des ordinateurs pour effectuer des opérations arithmétiques sur un très grand nombre rapidement.

Au début du 20e siècle, le mathématicien indien Srinivasa Ramanujan a trouvé beaucoup de nouvelles formules pour π, certains remarquables par leur élégance et la profondeur mathématique. Une de ses formules les plus célèbres est la série

qui fournit 14 chiffres par trimestre. Les frères Chudnovsky utilisé cette formule pour régler plusieurs dossiers informatiques π dans la fin des années 1980, y compris le premier calcul de plus d'un milliard (1011196691) décimales en 1989. Il reste la formule de choix pour le calcul de π logiciel qui se exécute sur les ordinateurs personnels, par opposition à la superordinateurs utilisés pour établir des records modernes.

Alors que la série augmentent généralement la précision avec un montant fixe pour chaque terme ajouté, il existe des algorithmes itératifs qui multiplient le nombre de chiffres corrects à chaque étape, avec l'inconvénient que chaque étape nécessite généralement un calcul coûteux. Une percée a été faite en 1975, quand Richard Brent et Eugene Salamin découvert indépendamment du Brent-Salamin algorithme, qui utilise seulement arithmétique de doubler le nombre de chiffres corrects à chaque étape. L'algorithme consiste à mettre en

et l'itération

jusqu'à ce qu'un _n et b _n sont suffisamment proches. Puis l'estimation de π est donné par

.

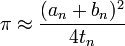En utilisant ce schéma, 25 itérations suffisent pour atteindre 45 millions de décimales correctes. Un algorithme similaire qui multiplie par quatre la précision dans chaque étape a été trouvé par Jonathan et Peter Borwein. Les méthodes ont été utilisées par Yasumasa Kanada et l'équipe pour définir la plupart des dossiers de calcul de π depuis 1980, jusqu'à un calcul de 206 158 430 000 décimales de π en 1999. Le record actuel est 1.241.100.000.000 décimales, fixés par Kanada et de l'équipe en 2002. Bien que la plupart des dossiers antérieurs de Kanada ont été fixés en utilisant l'algorithme Brent-Salamin, le calcul 2002 fait usage de deux formules de Machin qui étaient plus lent, mais cruciale réduit la consommation de mémoire. Le calcul a été effectué sur un 64-noeud avec une superordinateur Hitachi téraoctet de mémoire principale, capable d'effectuer 2000000000000 opérations par seconde.

Un important développement récent a été la Formule BBP (formule BBP), découvert par Simon Plouffe et nommé d'après les auteurs de l'article dans lequel la formule a d'abord été publié, David H. Bailey, Peter Borwein et Plouffe. La formule,

est remarquable, car il permet l'extraction de toute personne hexadécimal ou binaire chiffres de π sans calculer toutes les précédentes. Entre 1998 et 2000, le projet de calcul distribué PiHex utilisé une modification de la formule en raison de BBP Fabrice Bellard pour calculer la quadrillionième (1,000,000,000,000,000: e) peu de π, qui se est avéré être 0.

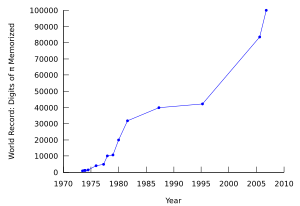
Mémorisation des chiffres

Récent décennies ont vu une augmentation du nombre record de chiffres mémorisés.

Même longtemps avant que les ordinateurs ont calculé π, la mémorisation d'un nombre record de chiffres est devenue une obsession pour certains. En 2006, Akira Haraguchi, un ingénieur japonais à la retraite, a affirmé avoir récité 100 000 décimales. Ceci, cependant, doit encore être vérifié par le Guinness World Records. Le record Guinness reconnu pour les chiffres rappelés de π est 67890 chiffres, détenues par Lu Chao, un étudiant diplômé de 24 ans en provenance de Chine. Il lui a fallu 24 heures et 4 minutes à réciter à la décimale 67890e de π sans erreur.

Il existe de nombreux moyens pour mémoriser π, y compris l'utilisation de "piems", qui sont des poèmes qui représentent π de telle sorte que la longueur de chaque mot (en lettres) représente un chiffre. Voici un exemple d'une piem: Comment je ai besoin d'un verre, alcoolique dans la nature (ou: bien sûr)., Après les conférences lourds impliquant la mécanique quantique Remarquez comment le premier mot a trois lettres, le deuxième mot a une, le troisième a 4, le quatrième a une, la cinquième a 5, et ainsi de suite. Le Cadaeic Cadenza contient les 3834 premiers chiffres de π de cette manière. Piems sont liés à l'ensemble du champ de l'étude d'humour mais sérieuse qui implique l'utilisation de techniques mnémotechniques pour se souvenir des chiffres de π, connus sous le nom Piphilology. Voir mnémoniques de Pi pour des exemples. Dans d'autres langues il existe des méthodes similaires de mémorisation. Cependant, cette méthode se avère inefficace pour un grand mémorisations de pi. D'autres méthodes incluent modèles retenir sur les chiffres; par exemple, l'année 1971 apparaît dans les cinquante premiers chiffres de pi.

Propriétés avancées

Approximations numériques

En raison de la nature transcendantale de π, il n'y a pas de formulaire expressions fermés pour le nombre en termes de nombre et fonctions algébriques. Les formules de calcul π en utilisant l'arithmétique élémentaire comprennent généralement série ou notation de sommation (tels que "..."), ce qui indique que la formule est une formule pour vraiment une séquence infinie d'approximations de π. Les plus termes inclus dans un calcul, la plus proche de π le résultat obtiendra.

Par conséquent, les calculs numériques doivent utiliser approximations de π. Pour de nombreuses raisons, ou 3,14 _^22/7 est assez proche, bien que les ingénieurs utilisent souvent 3,1416 (5 chiffres significatifs) ou 3,14159 (six chiffres significatifs) pour plus de précision. Les approximations _^22/7 et _^355/113, avec 3 et 7 chiffres significatifs respectivement, sont obtenues à partir de la simple développement en fraction continue de π. Le rapprochement _^355/113 (3,1415929 ...) est le meilleur qui peut être exprimé avec un à trois chiffres ou quatre chiffres numérateur et le dénominateur .

La première approximation numérique de π est presque certainement la valeur 3. Dans les cas où peu de précision est nécessaire, il peut être un substitut acceptable. Ce 3 est une sous-estimation découle du fait que ce est le rapport de la un périmètre de inscrit régulière hexagonale au diamètre du cercle .

Naturel

En géométrie non-euclidienne la somme des angles d'un triangle peut être supérieure ou inférieure à π radians , et le rapport de la circonférence d'un cercle à son diamètre peut également être différent de π. Cela ne change pas la définition de π, mais il ne affecte de nombreuses formules dans lesquelles π apparaît. Ainsi, en particulier, π ne est pas affectée par la forme de l'Univers; ce ne est pas un constante physique, mais une constante mathématique définie indépendamment de tout mesures physiques. Néanmoins, il se produit souvent en physique.

Par exemple, considérons la loi de Coulomb ( Unités SI):

Ici, quatre πr ² ne est que la surface de sphère de rayon r. Dans cette forme, ce est un moyen pratique de décrire la relation inverse du carré de la force à une distance r d'une source ponctuelle. Il serait bien sûr possible de décrire cette loi dans d'autres, mais moins pratique façons, ou dans certains cas plus pratique. Si Charge de Planck est utilisé, il peut être écrit comme

et éliminer ainsi la nécessité de π.

Questions ouvertes

La question ouverte la plus pressante à propos de π est de savoir si ce est un nombre normal - si un bloc de chiffres se produit dans l'expansion de π aussi souvent que l'on peut se attendre statistiquement si les chiffres avaient été produites entièrement "au hasard", et que ce est vrai dans toutes les bases, pas baser juste 10. Les connaissances actuelles sur cette point est très faible; par exemple, il ne est pas encore connu que des chiffres 0, ..., 9 se produisent souvent en continu dans le développement décimal de π.

Bailey et Crandall ont montré en 2000 que l'existence de l'mentionnés ci-dessus Formule BBP et des formules similaires impliquent que la normalité en base 2 de π et de divers autres constantes peut être réduite à une plausible conjecture de la théorie du chaos .

Il est également inconnu si π et e sont algébriquement indépendants, bien que Yuri Nesterenko a prouvé l'indépendance algébrique de {π, e ^π, Γ (1/4)} en 1996. Cependant, on sait que au moins un des πe et π + e est transcendantale (voir Théorème Lindemann-Weierstrass).

Utilisez en mathématiques et en sciences

π est omniprésent dans les mathématiques, apparaissant même dans les endroits qui ne ont pas un lien évident avec les cercles de la géométrie euclidienne.

Géométrie et la trigonométrie

Pour tout cercle de rayon r et de diamètre d = 2 r, la circonférence est π D et la région est π r ^2. En outre, π apparaît dans les formules pour les zones et les volumes de nombreuses autres formes géométriques basés sur des cercles, comme des ellipses , des sphères , cônes, et Tori . En conséquence, π apparaît dans intégrales définies qui décrivent circonférence, surface ou le volume des formes générées par des cercles. Dans le cas de base, la moitié de la superficie de la Unité de disque est donnée par:

et

donne la moitié de la circonférence de la cercle unité. Des formes plus complexes peuvent être intégrées en tant que solides de révolution.

De la définition unité cercle des fonctions trigonométriques suit également que le sinus et cosinus ont période 2π. Ce est, pour tout x et n entiers, sin (x) = sin (x + n 2π) et cos (x) = cos (x + n 2π). Parce que le péché (0) = 0, sin (2π n) = 0 pour tout entier n. En outre, la mesure d'angle de 180 ° est égale à π radians. En d'autres termes, 1 ° = (π / 180) radians.

En mathématiques modernes, π est souvent définie en utilisant les fonctions trigonométriques, par exemple comme les plus petites x positifs pour lesquels sin x = 0, pour éviter la dépendance inutile sur les subtilités de la géométrie euclidienne et l'intégration. Équivalente, π peut être définie en utilisant la fonctions trigonométriques inverses, comme par exemple π 2 = arccos (0) = π 4 ou arctan (1). Élargir fonctions trigonométriques inverses que série de puissance est la meilleure façon de tirer série infinie de π.

Analyse supérieur et de la théorie des nombres

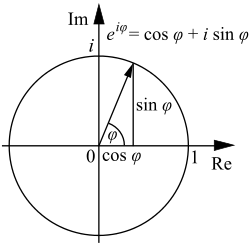
L'apparition fréquente de π dans analyse complexe peut être liée au comportement de la fonction exponentielle d'une variable complexe, décrit par La formule d'Euler

où i est l' unité imaginaire satisfaire i ² = -1 et e ≈ 2,71828 est Nombre d'Euler. Cette formule implique que les pouvoirs imaginaires décrivent des rotations de l'e sur le cercle unité dans le plan complexe; ces rotations ont une période de 360 ° = 2π. En particulier, les 180 ° = π φ résultats rotation dans le remarquable identité d'Euler

Il existe différents n n -ième racines de l'unité

Le Intégrale de Gauss

Une conséquence est que le fonction de gamma d'un demi-entier est un multiple rationnel de √π.

Physique

Le nombre π apparaît régulièrement dans les équations décrivant des principes fondamentaux de l'Univers, dues en grande partie à sa relation avec la nature du cercle et, en conséquence, les systèmes de coordonnées sphérique.

• Le constante cosmologique:

• Le principe d'incertitude d'Heisenberg:

• L'équation de champ d'Einstein de la relativité générale :

• La loi de Coulomb pour la force électrique :

• La perméabilité magnétique d'espace libre:

• Troisième constante de la loi de Kepler :

Probabilités et statistiques

En probabilité et statistiques , il ya beaucoup de distributions dont les formules contiennent π, y compris:

• la fonction de densité de probabilité de la distribution normale de moyenne μ et d' écart type σ, en raison de la Intégrale gaussienne:

• la fonction de densité de probabilité pour la (standard) Distribution de Cauchy:

A noter que puisque 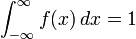pour une fonction de densité de probabilité f (x), les formules ci-dessus peuvent être utilisés pour produire d'autres formules intégrales pour π.

Le problème de l'aiguille de Buffon est parfois cité comme une approximation empirique de π dans «mathématiques populaires" fonctionne. Envisager de laisser tomber une aiguille de longueur L à plusieurs reprises sur une surface contenant des lignes parallèles tirés unités S en dehors (avec S> L). Si l'aiguille est tombé n fois et x de ces moments où il se immobilise en traversant une ligne (x> 0), alors on peut rapprocher π en utilisant la méthode de Monte Carlo :

Bien que ce résultat est mathématiquement impeccable, il ne peut pas être utilisée pour déterminer plus de très peu de chiffres de π par l'expérience. Obtenir de façon fiable seulement trois chiffres (y compris l'initiale «3») exige le droit des millions de lancers, et le nombre de lancers croît de façon exponentielle avec le nombre de chiffres souhaités. En outre, toute erreur dans la mesure de longueurs L et S transfère directement à une erreur dans le π approchée. Par exemple, une différence d'un seul atome de la longueur d'une aiguille de 10 centimètres apparaîtrait dans le neuvième chiffre du résultat. Dans la pratique, les incertitudes pour déterminer si l'aiguille traverse effectivement une ligne quand il apparaît à toucher exactement il limitera la précision atteignable à beaucoup moins de 9 chiffres.