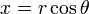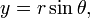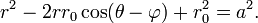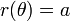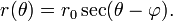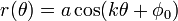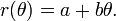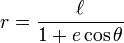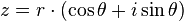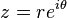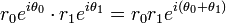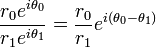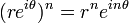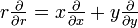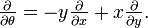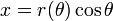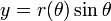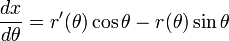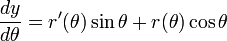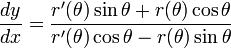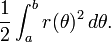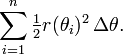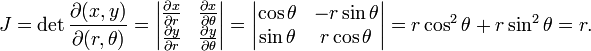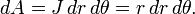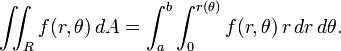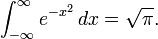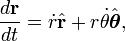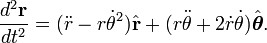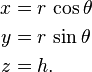Système de coordonnées polaires
Saviez-vous ...
SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille près de la charité. Lire la suite ...
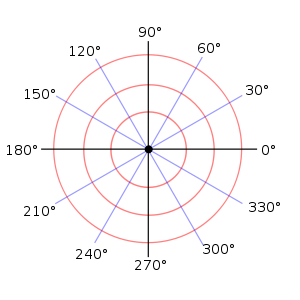
En mathématiques , le système de coordonnées polaires est un bidimensionnel système dans lequel chaque coordonnée point situé sur un plan est déterminée par un angle et une distance de . Le système de coordonnées polaires est particulièrement utile dans les situations où la relation entre deux points est la plus facile à exprimer en termes de distance et les angles; dans le plus familier cartésienne système ou coordonnées rectangulaires, une telle relation ne peut être trouvée par le biais trigonométriques formules.
Comme le système de coordonnées est à deux dimensions, chaque point est déterminée par deux coordonnées polaires: la coordonnée radiale et la coordonnée angulaire. La coordonnée radiale (généralement notée  ) Désigne la distance du point à partir d'un point central connu sous le pôle (équivalent à l'origine dans le système cartésien). La coordonnée angulaire (également connu comme l'angle polaire ou la angle d'azimut, et généralement désigné par θ ou
) Désigne la distance du point à partir d'un point central connu sous le pôle (équivalent à l'origine dans le système cartésien). La coordonnée angulaire (également connu comme l'angle polaire ou la angle d'azimut, et généralement désigné par θ ou  ) Désigne le positif ou dans le sens antihoraire (sens antihoraire) angle nécessaire pour atteindre le point de la 0 ° ray ou axe polaire (ce qui équivaut à la borne positive axe x dans le plan cartésien).
) Désigne le positif ou dans le sens antihoraire (sens antihoraire) angle nécessaire pour atteindre le point de la 0 ° ray ou axe polaire (ce qui équivaut à la borne positive axe x dans le plan cartésien).
Histoire
Les concepts d'angle et le rayon étaient déjà utilisées par les peuples anciens du 1er millénaire BCE. Le astronome Hipparque (190-120 BCE) a créé un tableau de fonctions accords donnant la longueur de la corde pour chaque angle, et il ya des références à son aide de coordonnées polaires dans l'établissement de positions stellaires. Dans Des spirales, Archimède décrit la Spirale d'Archimède, d'une fonction dont le rayon dépend de l'angle. Le travail grec, cependant, ne se étend pas à un système de coordonnées complète.
Il ya différents comptes de l'introduction de coordonnées polaires dans le cadre d'un système formel de coordonnées. L'histoire complète de l'objet est décrit dans Professeur à Harvard L'origine de Julian Lowell Coolidge des coordonnées polaires. Grégoire de Saint-Vincent-et- Bonaventura Cavalieri introduit indépendamment les concepts dans le milieu du XVIIe siècle. Saint-Vincent a écrit sur eux en privé en 1625 et publié son travail en 1647, tandis que Cavalieri a publié son en 1635 avec une version corrigée apparaissant en 1653. Cavalieri abord utilisé coordonnées polaires pour résoudre un problème lié à la zone dans un Spirale d'Archimède. Blaise Pascal ensuite utilisé pour calculer les coordonnées polaires de la longueur arcs paraboliques.
En Fluxion (écrit 1671, publié 1736), Sir Isaac Newton a examiné les transformations entre coordonnées polaires, qu'il dénommé le "septième manière; Pour Spirales", et neuf autres systèmes de coordonnées. Dans la revue Acta Eruditorum (1691), Jacob Bernoulli utilisé un système avec un point sur une ligne, appelle le pôle et l'axe polaire respectivement. Coordonnées été défini par la distance entre le pôle et l'angle de l'axe polaire. Le travail de Bernoulli étendu à trouver le rayon de courbure des courbes exprimées dans ces coordonnées.
Les coordonnées polaires terme réelle a été attribuée à Gregorio Fontana et a été utilisé par les écrivains italiens du 18e siècle. Le terme est apparu dans Anglais en 1816 traduction de George Peacock Lacroix calcul différentiel et intégral. Alexis Clairaut a été le premier à penser de coordonnées polaires en trois dimensions, et Leonhard Euler était le premier à réellement développer.
Tracer des points en coordonnées polaires
Chaque point dans le système de coordonnées polaires peut être décrite avec les deux coordonnées polaires, qui sont généralement appelés  (La coordonnée radiale) et θ (la coordonnée angulaire, angle polaire, ou angle d'azimut, parfois représenté comme φ ou
(La coordonnée radiale) et θ (la coordonnée angulaire, angle polaire, ou angle d'azimut, parfois représenté comme φ ou 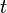 ). Le
). Le  coordonner représente la distance radiale à partir du poteau, et la coordination θ représente l'angle de 0 ° vers la gauche (sens antihoraire) rayon (parfois appelé axe polaire), connu sous l'axe des x positif sur le plan cartésien .
coordonner représente la distance radiale à partir du poteau, et la coordination θ représente l'angle de 0 ° vers la gauche (sens antihoraire) rayon (parfois appelé axe polaire), connu sous l'axe des x positif sur le plan cartésien .
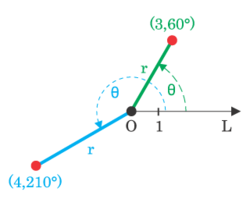
Par exemple, les coordonnées polaires (3, 60 °) serait tracée en un point 3 unités du pôle sur le rayon de 60 °. Les coordonnées (-3, 240 °) seront également tracées à ce moment parce que la distance radiale négative est mesurée comme une distance positive sur le rayon opposé (le rayon réfléchi sur l'origine, qui diffère du rayon initial de 180 °).
Un aspect important du système de coordonnées polaires, pas présent dans le système de coordonnées cartésiennes, ce est que d'un seul point peut être exprimé avec un nombre infini de coordonnées différents. En effet, ne importe quel nombre de révolutions multiples peut être réalisé autour du pôle central sans affecter la position réelle du point tracé. En général, le point (  , Θ) peut être représenté par (
, Θ) peut être représenté par (  , Θ ±
, Θ ± 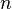 × 360 °) ou (-
× 360 °) ou (-  , Θ ± (2
, Θ ± (2 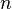 + 1) 180 °), où
+ 1) 180 °), où 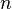 est ne importe quel nombre entier .
est ne importe quel nombre entier .
Les coordonnées arbitraires (0, θ) sont classiquement utilisées pour représenter le pôle, que quel que soit le θ coordonner, un point de rayon 0 sera toujours sur le poteau. Pour obtenir une représentation unique d'un point, il est habituel de limiter  pour les numéros non-négatifs
pour les numéros non-négatifs  ≥ 0 et θ à la intervalle [0, 360 °) ou (-180 °, 180 °] (ou, en radians, [0, 2π) ou (-π, π]).
≥ 0 et θ à la intervalle [0, 360 °) ou (-180 °, 180 °] (ou, en radians, [0, 2π) ou (-π, π]).
Angles en notation polaire sont généralement exprimées en degrés ou en radians , en utilisant les deux conversion π rad = 360 °. Le choix dépend en grande partie du contexte. Les applications de navigation utilisent mesure en degrés, tandis que certains physique applications (mécanique spécifiquement rotation) et presque toute la littérature mathématique sur le calcul utilisent radians.
Conversion entre coordonnées polaires et cartésiennes
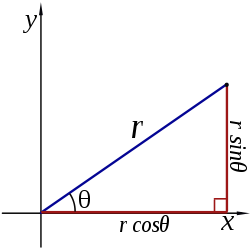
Les deux coordonnées polaires  et θ peuvent être convertis en les coordonnées cartésiennes
et θ peuvent être convertis en les coordonnées cartésiennes  et
et  à l'aide de la fonction trigonométrique sinus et le cosinus:
à l'aide de la fonction trigonométrique sinus et le cosinus:
tandis que les deux coordonnées cartésiennes  et
et  peuvent être convertis en coordonnées polaires
peuvent être convertis en coordonnées polaires  par
par
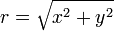 (Par une simple application de la théorème de Pythagore ).
(Par une simple application de la théorème de Pythagore ).
Pour déterminer l'angle θ de coordonnées, les deux idées suivantes doivent être envisagées:
- Pour
 = 0, θ peut être réglé sur toute valeur réelle .
= 0, θ peut être réglé sur toute valeur réelle . - Pour
 ≠ 0, pour obtenir une représentation unique pour θ, elle doit être limitée à un intervalle de taille 2π. Choix classiques pour un tel intervalle sont [0, 2π) et (-π, π].
≠ 0, pour obtenir une représentation unique pour θ, elle doit être limitée à un intervalle de taille 2π. Choix classiques pour un tel intervalle sont [0, 2π) et (-π, π].
Pour obtenir θ dans l'intervalle [0, 2π), ce qui suit peut être utilisé ( 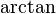 désigne l'inverse de la tangente fonction):
désigne l'inverse de la tangente fonction):
Pour obtenir θ dans l'intervalle (-π, π], celui-ci peut être utilisé:
On peut éviter d'avoir à garder une trace des signes de numérateur et dénominateur par l'utilisation de la atan2 fonction, qui a des arguments distincts pour le numérateur et le dénominateur.
Équations polaires
L'équation définissant une courbe algébrique exprimée en coordonnées polaires est connue comme une équation polaire. Dans de nombreux cas, une telle équation peut simplement être spécifié en définissant  en tant que fonction de θ. La courbe obtenue est alors constitué de points de la forme (
en tant que fonction de θ. La courbe obtenue est alors constitué de points de la forme (  (Θ), θ), et peut être considérée comme la graphe de la fonction polaire
(Θ), θ), et peut être considérée comme la graphe de la fonction polaire  .
.
Différentes formes de symétrie peuvent être déduites à partir de l'équation d'une fonction polaire  . Si
. Si  (-θ) =
(-θ) =  (Θ) de la courbe sera symétrique par rapport au rayon horizontal (0 ° / 180 °), si
(Θ) de la courbe sera symétrique par rapport au rayon horizontal (0 ° / 180 °), si  (Π-θ) =
(Π-θ) =  (Θ), il sera symétrique par rapport à la (90 ° / 270 °) rayon vertical, et si
(Θ), il sera symétrique par rapport à la (90 ° / 270 °) rayon vertical, et si  (Θ-α °) =
(Θ-α °) =  (Θ), il sera α ° à symétrie de révolution dans le sens antihoraire autour du pôle.
(Θ), il sera α ° à symétrie de révolution dans le sens antihoraire autour du pôle.
En raison de la nature circulaire du système de coordonnées polaires, de nombreuses courbes peuvent être décrites par une équation polaire plutôt simple, tandis que leur forme cartésienne est beaucoup plus complexe. Parmi les plus connus de ces courbes sont les Polar Rose, Spirale d'Archimède, lemniscate, limaçon, et cardioïde.
Pour le cercle, la ligne et rose polaire ci-dessous, il est entendu qu'il n'y a pas de restrictions sur le domaine et de la courbe.
Cercle

 (Θ) = 1
(Θ) = 1 L'équation générale pour un cercle avec un centre au (  0, φ) et le rayon
0, φ) et le rayon 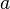 est
est
Cela peut être simplifiée de diverses manières, afin de se conformer à des cas plus particuliers, comme l'équation
pour un cercle avec un centre au niveau du pôle et de rayon 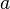 .
.
Ligne
Lignes radiales (ceux fonctionnant par le pôle) sont représentés par l'équation
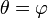 ,
,
où φ est l'angle d'élévation de la ligne; ce est-à φ = arctan  où
où  est le pente de la droite dans le système de coordonnées cartésiennes. La ligne non radial qui traverse les = φ de la ligne radiale perpendiculairement au point (
est le pente de la droite dans le système de coordonnées cartésiennes. La ligne non radial qui traverse les = φ de la ligne radiale perpendiculairement au point (  0, φ) a l'équation
0, φ) a l'équation
Polar Rose
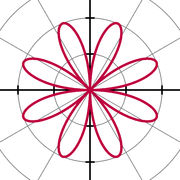
 (Θ) = 2 sin 4θ
(Θ) = 2 sin 4θ Un rose polaire est une courbe mathématique célèbre qui ressemble à une fleur pétales, et qui peut être exprimé en équation polaire simple,
pour ne importe quelle constante 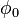 (Y compris 0). Si k est un nombre entier, ces équations produira un -petalled k si k est augmenté impair, ou 2 k -petalled augmenté si k est pair. Si k est rationnel mais pas un nombre entier, une forme de rose comme peut former, mais avec des pétales qui se chevauchent. On notera que ces équations définissent jamais une rose avec 2, 6, 10, 14, etc. pétales. Le une variable représentant la longueur des pétales de la rose.
(Y compris 0). Si k est un nombre entier, ces équations produira un -petalled k si k est augmenté impair, ou 2 k -petalled augmenté si k est pair. Si k est rationnel mais pas un nombre entier, une forme de rose comme peut former, mais avec des pétales qui se chevauchent. On notera que ces équations définissent jamais une rose avec 2, 6, 10, 14, etc. pétales. Le une variable représentant la longueur des pétales de la rose.
Spirale d'Archimède
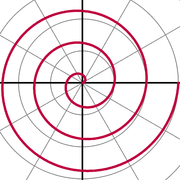
Le Spirale d'Archimède est une spirale célèbre qui a été découvert par Archimède , qui peut également être exprimé en équation polaire simple. Elle est représentée par l'équation
Modification du paramètre a tournera la spirale, tandis que b contrôle la distance entre les bras, qui, pour une spirale donnée est toujours constante. La spirale d'Archimède a deux bras, l'un pour θ> 0 et une pour θ <0. Les deux bras sont reliés en douceur au niveau du pôle. Prenant l'image miroir d'un bras à travers la ligne de 90 ° ° / 270 donnera l'autre bras. Cette courbe est remarquable comme l'une des premières courbes, après les sections coniques , être décrit dans un traité de mathématiques, et comme étant un excellent exemple d'une courbe qui est le mieux défini par une équation polaire.
Sections coniques
Une section conique avec un seul objectif sur le poteau et l'autre quelque part sur le rayon 0 ° (de sorte que de la conique grand axe se étend le long de l'axe polaire) est donnée par:
où e est la excentricité et 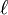 est le semi-latus rectum (la distance perpendiculaire à un foyer de l'axe majeur de la courbe). Si e> 1, cette équation définit une hyperbole; si e = 1, on définit un parabole; et si E <1, il définit une ellipse . Le cas spécial e = 0 des derniers résultats dans un cercle de rayon
est le semi-latus rectum (la distance perpendiculaire à un foyer de l'axe majeur de la courbe). Si e> 1, cette équation définit une hyperbole; si e = 1, on définit un parabole; et si E <1, il définit une ellipse . Le cas spécial e = 0 des derniers résultats dans un cercle de rayon 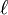 .
.
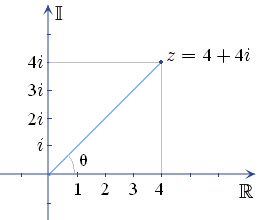
Les nombres complexes
Chaque nombre complexe peut être représenté par un point dans le plan complexe , et peut donc être exprimée soit en spécifiant les coordonnées cartésiennes est le point (appelées forme rectangulaire ou cartésienne) ou les coordonnées polaires de la virgule (appelée forme polaire). Le nombre complexe z peut être représenté sous forme rectangulaire
où i est l' unité imaginaire , ou peut alternativement être écrit sous forme polaire (via les formules de conversion donnés ci-dessus ) que
et à partir de là que
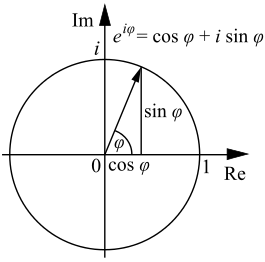
où e est Le nombre d'Euler, qui sont équivalentes, comme indiqué par La formule d'Euler. (Notez que cette formule, comme tous ceux qui impliquent des angles exponentielles, suppose que l'angle θ est exprimé en radians). Pour une conversion entre les formes rectangulaires et polaires d'un nombre complexe, les formules de conversion indiquées ci-dessus peuvent être utilisés.
Pour les opérations de multiplication , division et exponentiation des nombres complexes, il est généralement beaucoup plus simple de travailler avec des nombres complexes exprimées sous forme polaire plutôt que la forme rectangulaire. Des lois de la exponentiation:
- Multiplication:
- Division:
- Exponentiation ( La formule de De Moivre):
Calcul
Calcul peut être appliquée à des équations exprimées en coordonnées polaires.
Le θ coordonnée angulaire est exprimé en radians au long de cette section, qui est le choix classique lorsque vous faites le calcul.
Calcul différentiel
Nous avons les formules suivantes:
Pour trouver la pente cartésienne de la tangente à une courbe r polaire (θ) à un moment donné, la courbe est d'abord exprimée comme un système de équations paramétriques.
Différencier les deux équations par rapport aux rendements θ
La division de la seconde équation par les premiers rendements cartésien la pente de la tangente à la courbe au point (r, r (θ)):
Calcul intégral
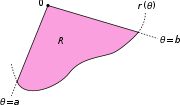
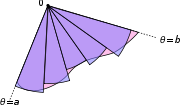
Soit R désignent la région délimitée par une courbe r (θ) et les rayons θ = a et θ = b, où 0 <b - un <2π. Ensuite, la zone de R est
Ce résultat peut être trouvé comme suit. En premier lieu, l'intervalle [a, b] est divisée en n sous-intervalles, où n est un nombre entier positif arbitraire. Ainsi Δθ, la longueur de chaque sous-intervalle, est égal à b - a (la longueur totale de l'intervalle), divisée par n, le nombre de sous-intervalles. Pour chaque sous-intervalle i = 1, 2, ..., n, permettez θ i le point médian de la sous-intervalle, et de construire un secteur avec le centre au pôle, rayon r (θ i), angle central Δθ et longueur d'arc 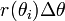 . La superficie de chaque secteur construit est donc égale à
. La superficie de chaque secteur construit est donc égale à 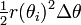 . Par conséquent, la surface totale de l'ensemble des secteurs est
. Par conséquent, la surface totale de l'ensemble des secteurs est
Comme le nombre de sous-intervalles n est augmentée, le rapprochement de la zone continue de se améliorer. Dans la limite N → ∞, la somme devient le Somme de Riemann pour l'intégrale ci-dessus.
Généralisation
Utilisation de coordonnées cartésiennes , un élément de la zone infinitésimale peut être calculée comme dA = dx dy. Le règle de substitution pour les intégrales multiples indique que, lors de l'utilisation d'autres coordonnées, les Déterminant jacobien de la formule de coordonner de conversion doit être considéré:
Par conséquent, un élément de surface en coordonnées polaires peut se écrire
Maintenant, une fonction qui est donné en coordonnées polaires peut être intégré comme suit:
Ici, R est la même région que précédemment, à savoir, la région délimitée par une courbe r (θ) et les rayons θ = θ a et b =.
La formule pour le domaine de la R mentionné ci-dessus est récupéré en prenant f identiquement égale à 1. Une application plus surprenant de ce résultat donne le Intégrale de Gauss
Calcul vectoriel
Vecteur calcul peut également être appliquée à des coordonnées polaires. Laisser  le vecteur de position
le vecteur de position 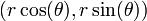 , Où r et
, Où r et 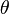 en fonction du temps t,
en fonction du temps t, 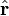 être un vecteur unitaire dans la direction
être un vecteur unitaire dans la direction  et
et 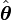 être un vecteur unitaire perpendiculaire à
être un vecteur unitaire perpendiculaire à  . Les première et seconde positions sont des dérivés de
. Les première et seconde positions sont des dérivés de
Trois dimensions
Le système de coordonnées polaires est étendu en trois dimensions avec deux systèmes de coordonnées différents systèmes de coordonnées, la cylindrique et sphérique, deux qui comprennent deux dimensions ou coordonnées polaires planes comme un sous-ensemble. Essentiellement, le système de coordonnées cylindrique se étend coordonnées polaires par l'ajout d'une distance supplémentaire de coordonnées, tandis que le système sphérique ajoute un supplément de place coordonnée angulaire.
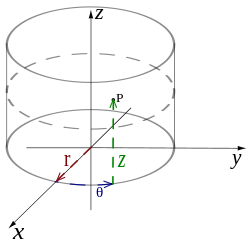
Coordonnées cylindriques
Le système de coordonnées cylindrique est un système de coordonnées qui se étend essentiellement à deux dimensions le système de coordonnées polaires par l'ajout d'une troisième coordonnée à mesurer la hauteur d'un point au-dessus du plan, similaire à la manière dont le système de coordonnées cartésiennes se étend dans trois dimensions. La troisième coordonnée est habituellement notée h, rendant les trois coordonnées cylindriques (r, θ, h).
Les trois coordonnées cylindriques peuvent être converties en coordonnées cartésiennes par:
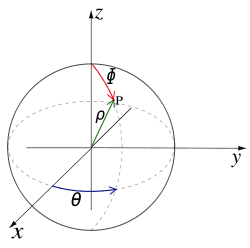
Coordonnées sphériques
Les coordonnées polaires peuvent également être étendues en trois dimensions en utilisant les coordonnées (ρ, φ, θ), où ρ est la distance de l'origine, φ est l'angle de l'axe z (appelé colatitude ou zénith et mesurée 0-180 °) et θ est l'angle de l'axe x (comme dans les coordonnées polaires). Ce système de coordonnées, appelé le système de coordonnées sphériques, est similaire à la latitude et Système de longitude utilisé pour la Terre, à l'origine dans le centre de la Terre, la latitude de δ étant le complément de φ, déterminée par δ = 90 ° - φ, la longitude et l étant mesurée par l = θ - 180 °.
Les trois coordonnées sphériques sont converties en coordonnées cartésiennes par:
Applications
Les coordonnées polaires sont à deux dimensions et par conséquent ils peuvent être utilisés que lorsque la position des points se trouvent sur un seul plan à deux dimensions. Ils sont les plus appropriées dans un contexte où le phénomène étant considéré est intrinsèquement liée à la direction et la longueur d'un point central. Par exemple, les exemples ci-dessus montrent comment des équations polaires élémentaires suffisent à définir des courbes - comme la spirale d'Archimède - dont l'équation dans le système de coordonnées cartésiennes seraient beaucoup plus complexe. En outre, de nombreux systèmes physiques - tels que ceux concernés par les corps en mouvement autour d'un point central ou à des phénomènes provenant d'un point central - sont plus simple et plus intuitive pour modéliser en coordonnées polaires. La motivation initiale pour l'introduction du système polaire était l'étude de circulaire et mouvement orbital.
Les coordonnées polaires sont souvent utilisés dans la navigation, la destination ou la direction de Voyage peuvent être donnés comme un angle et la distance de l'objet à l'étude. Par exemple, les aéronefs utilisent une version légèrement modifiée des coordonnées polaires pour la navigation. Dans ce système, celui généralement utilisé pour toute sorte de navigation, le rayon de 0 ° est généralement appelée la position 360, et les angles continue dans un le sens horaire, plutôt que dans le sens antihoraire, comme dans le système mathématique. Rubrique 360 correspond à nord magnétique, tout en rubriques 90, 180 et 270 correspondent à l'est magnétique, le sud et à l'ouest, respectivement. Ainsi, un avion voyageant 5 miles nautiques à l'est se rendront cinq unités au titre 90 (lire niner-zéro contrôle du trafic aérien).
Modélisation
Systèmes d'affichage symétrie radiale fournir milieux naturels pour le système de coordonnées polaires, avec le point central agissant comme le pôle. Un excellent exemple de cet usage est le équation d'écoulement des eaux souterraines lorsqu'il est appliqué aux puits radialement symétriques. Systèmes avec un force radiale sont également de bons candidats pour l'utilisation du système de coordonnées polaires. Ces systèmes comprennent les champs gravitationnels , qui obéissent à la loi de l'inverse carré, ainsi que des systèmes avec des sources ponctuelles, telles que antennes radio.
Radialement systèmes asymétriques peuvent également être modélisés avec des coordonnées polaires. Par exemple, un du microphone motif ramassage illustre sa réponse proportionnelle à un son en provenance d'un sens donné, et ces motifs peuvent être représentés sous forme de courbes polaires. La courbe pour un microphone cardioïde standard, le microphone unidirectionnel le plus commun, peut être représenté comme r = 0,5 + 0,5 péché θ.