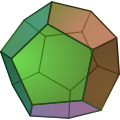
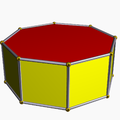
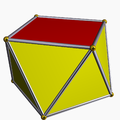
Polyèdre
Saviez-vous ...
SOS Enfants, qui se déroule près de 200 sos écoles dans le monde en développement, a organisé cette sélection. Parrainage d'enfants aide les enfants du monde en développement à apprendre aussi.
|
Un polyèdre (polyèdres ou polyèdres pluriel) est souvent défini comme un géométrique objet à faces planes et des bords droits (le mot vient du polyèdre grec classique πολυεδρον, de poly, tige de πολυς, "beaucoup," + -edron, sous forme de εδρον, «base», «siège» ou «face»).
Cette définition d'un polyèdre est pas très précise, et un mathématicien moderne est tout à fait insatisfaisante. Grünbaum (1994, p.43) a observé que:
Le Original Sin dans la théorie des polyèdres remonte à Euclid , et par Kepler , Poinsot, Cauchy et bien d'autres ... [dans cette] à chaque étape ... les écrivains ne ont pas réussi à définir ce que sont les «polyèdres '...
Mathématiciens modernes ne ont même pas d'accord sur exactement ce qui fait quelque chose d'un polyèdre.
Qu'est-ce qu'un polyèdre?
Nous pouvons dire que au moins un polyèdre est construit à partir de différents types d'élément ou d'une entité, chacune associée à un nombre différent de dimensions:
- Trois dimensions: Le corps est délimité par des faces, et est habituellement le volume intérieur.
- Deux dimensions: A le visage est délimitée par un circuit de bords, et est habituellement une région (plane) appelle un polygone . Les visages forment ensemble la surface polyédrique.
- Une dimension: Un bord rejoint un sommet à l'autre et une face à l'autre, et est habituellement un ligne d'une certaine sorte. Les bords forment ensemble le squelette polyédrique.
- 0 dimensions: A sommet (Les sommets pluriel) est un coin Point.
- Dimension -1: La nullité est une sorte de non-entité tenue par abstraites théories.
Plus généralement, dans les mathématiques et les autres disciplines, "polyèdre" est utilisé pour désigner une variété de constructions connexes, dont certains géométrique et d'autres purement algébrique ou abstraite.
Une caractéristique déterminante de presque tous les types de polyèdres est que seulement deux visages rejoignent le long d'une arête commune. Cela garantit que la surface polyédrique est continuellement connecté et ne se arrête pas brusquement ou scission dans des directions différentes.
Un polyèdre est un exemple trois dimensions de la plus générale polytope dans un nombre quelconque de dimensions.
Caractéristiques
Polyèdres Naming
Les polyèdres sont souvent nommés selon le nombre de faces. Le système de nommage est à nouveau basé sur grec classique, par exemple tétraèdre (4), pentaèdre (5), hexaèdre (6), heptaèdre (7), triacontaèdre (30), et ainsi de suite.
Souvent, cela est qualifié par une description des types de visages présents, par exemple, le Dodécaèdre rhombique contre la Dodécaèdre pentagonal.
Autres noms communs indiquent que certaines opération ne est effectuée sur un polyèdre simple, par exemple le cube tronqué ressemble à un cube avec ses coins coupés, et dispose de 14 visages (il est aussi un exemple de tetrakaidecahedron).
Certains polyèdres spéciale ont augmenté leurs propres noms au fil des ans, comme Le monstre de Miller ou Polyèdre Szilassi.
Bords
Bords ont deux caractéristiques importantes (sauf si le polyèdre est complexe ):
- Une arête rejoint seulement deux sommets.
- Une arête rejoint seulement deux visages.
Ces deux caractéristiques sont à deux les uns aux autres.
Caractéristique d'Euler
La caractéristique d'Euler χ concerne le nombre de sommets V, bords E, F et fait face d'un polyèdre:
- χ = V - E + F.
Pour un polyèdre simplement connecté, χ = 2. Pour une discussion détaillée, voir Preuves et Réfutations par Imre Lakatos.
Dualité

Pour chaque polyèdre il ya un polyèdre dual comportant des faces en place des sommets de l'original et vice versa. Dans la plupart des cas, le double peut être obtenu par le procédé de déplacement alternatif sphérique.
Figure de sommet
Pour chaque sommet on peut définir un Figure de sommet constitué des sommets relié à lui. Le sommet est dite régulière si ce est un polygone régulier et symétrique par rapport à l'ensemble du polyèdre.
Polyèdres traditionnelle
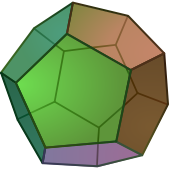
En géométrie , un polyèdre est traditionnellement une forme tridimensionnelle qui est constituée d'un nombre fini de polygonal faces qui sont des parties de plans ; les faces se rencontrent en paires le long de bords qui sont en ligne droite segments, et les bords se rencontrent aux points appelé sommets. Cubes , prismes et pyramides sont des exemples de polyèdres. Le polyèdre entourant un volume délimité dans l'espace tridimensionnel; parfois ce volume intérieur est considéré comme faisant partie du polyèdre, parfois seulement la surface est pris en considération, et, occasionnellement, que le squelette d'arêtes.
Un polyèdre est dit être Convexe si sa surface (comprenant ses faces, arêtes et sommets) ne lui-même et le segment de ligne joignant deux points quelconques du polyèdre coupe pas est contenu à l'intérieur et la surface.
Polyèdres symétriques
Beaucoup de polyèdres les plus étudiés sont très symétriques .
Bien sûr, il est facile de fausser tels polyèdres de sorte qu'ils ne sont plus symétriques. Mais où un nom polyédrique est donnée, comme icosidodécaèdre, la géométrie la plus symétrique est presque toujours implicite, sauf indication contraire.
Certains des noms les plus communs en particulier sont souvent utilisés avec "régulière" devant ou implicite, car pour chaque Il existe différents types qui ont peu en commun, sauf pour avoir le même nombre de visages. Ce sont les tétraèdre , le cube , l'octaèdre , dodécaèdre et icosaèdre:
Polyèdres des plus hautes symétries ont tous un certain type d'élément - visages, bords et / ou des sommets, dans une seule orbite de symétrie. Il ya différentes catégories de tels polyèdres:
- Isogonal ou Vertex-transitif si tous les sommets sont les mêmes, en ce sens que pour deux sommets il existe un symétrie du polyèdre cartographie de la première isométrique sur la seconde.
- Isotoxal ou Edge-transitif si toutes les arêtes sont les mêmes, en ce sens que pour toutes les deux bords, il existe une symétrie de la cartographie du premier polyèdre isométriquement sur la seconde.
- Isoedrique ou Face-transitif si toutes les faces sont identiques, en ce sens que pour toutes les deux faces, il existe une symétrie de la cartographie du premier polyèdre isométriquement sur la seconde.
- Régulier se il est vertex-transitive, bord-transitive et face transitive (ce qui implique que chaque visage est le même polygone régulier; elle implique aussi que chaque sommet est régulier).
- Quasi-régulière si elle est transitive et vertex-bord transitive (et a donc visages réguliers) mais pas en face-transitive. Une double quasi-régulière est face transitive et le bord transitive (et donc chaque sommet est régulière), mais pas vertex-transitive.
- Semi-régulier se il est sommet-transitif mais pas EDGE-transitive, et chaque visage est un polygone régulier. (Ce est l'une de plusieurs définitions du terme, selon l'auteur. Certaines définitions se chevauchent avec la classe quasi-régulière). Une double semi-régulière est face transitive mais pas Vertex transitive, et chaque sommet est régulière.
- Homogène si elle est vertex-transitive et chaque visage est un polygone régulier, ce est à dire qu'il est régulier, quasi-régulière ou semi-régulière. Une double uniforme est face transitive et a sommets réguliers, mais ne est pas nécessairement sommet-transitif).
- Noble se il est face transitive et vertex-transitif (mais pas nécessairement bord transitive). Les polyèdres réguliers sont aussi noble; ils sont la seule polyèdres uniformes noble.
Un polyèdre peut appartenir au même groupe de symétrie globale comme une de symétrie élevé, mais aura plusieurs groupes d'éléments (par exemple faces) dans différentes orbites de symétrie.
Polyèdres uniformes et leurs duals
Polyèdres uniformes sont sommet-transitif et chaque visage est un polygone régulier. Ils peuvent être régulière, quasi-régulière ou semi-régulière, et peut être convexe ou étoilé.
L'uniforme duals sont face transitive et chaque vertex chiffre est un polygone régulier.
Face-transitivité d'un polyèdre correspond à vertex-transitivité de la double et inversement, et le bord-transitivité d'un polyèdre correspond à bord transitivité de la double. Dans la plupart des duels de polyèdres uniformes, faces sont des polygones irréguliers. Le polyèdres réguliers sont une exception, car ils sont à double à l'autre.
Chaque polyèdre uniforme part la même symétrie que son double, avec les symétries de visages et de sommets tout simplement inversés. Pour cette raison certaines autorités considèrent les duels aussi uniforme aussi. Mais cette idée ne est pas largement répandue: un polyèdre et ses symétries ne sont pas la même chose.
Le polyèdres uniformes et leurs duals sont traditionnellement classés selon leur degré de symétrie, et si elles sont convexe ou non.
| Uniforme convexe | Uniforme convexe double | Étoile uniforme | Étoile uniforme double | |
|---|---|---|---|---|
| Régulier | Solides platoniciens | Kepler-Poinsot polyèdres | ||
| Quasiregular | Solides d'Archimède | Solides de Catalan | (Pas de nom particulier) | (Pas de nom particulier) |
| Semi-régulière | (Pas de nom particulier) | (Pas de nom particulier) | ||
| Prismes | Dipyramids | Étoile Prismes | Étoile Dipyramids | |
| Antiprismes | Trapézoèdres | Étoile Antiprismes | Étoile Trapézoèdres | |
Polyèdres Noble
Un noble polyèdre est à la fois isoedrique (égale à face) et isogonal (égale cornes). Outre le polyèdres réguliers, il ya beaucoup d'autres exemples.
Le double d'un noble polyèdre est aussi noble.
groupes de symétrie
Le polyédrique groupes de symétrie sont toutes et des groupes de points comprennent:
- T - chiral symétrie tétraédrique; le groupe de rotation pour un habitué tétraèdre ; Afin 12.
- T d - complète symétrie tétraédrique; le groupe de symétrie pour un habitué tétraèdre ; Afin 24.
- T h - pyritohedral symétrie; Afin 24. La symétrie d'un pyritohedron.
- O - chiral symétrie octaédrique; le groupe de la rotation de cube et octaèdre ; Afin 24.
- O h - complète symétrie octaédrique; le groupe de symétrie du cube et l'octaèdre ; Afin 48.
- I - chiral symétrie icosaédrique; le groupe de rotation de la et l'icosaèdre dodécaèdre; Afin 60.
- I h - pleins symétrie icosaédrique; le groupe de symétrie de la et l'icosaèdre dodécaèdre; commander 120.
- C nv - n -fois symétrie pyramidale
- D nh - n -fois symétrie prismatique
- D nv - n -fois symétrie antiprismatique
Ceux avec symétrie chirale ne ont pas symétrie de réflexion et donc avoir deux formes énantiomorphes qui sont les reflets de l'autre. Les freinages polyèdres Archimède ont cette propriété.
Autres polyèdres à faces régulières
Visages réguliers égalité
Quelques familles de polyèdres, où chaque visage est le même genre de polygone:
- Deltaèdres ont triangles équilatéraux pour les visages.
- En ce qui concerne les polyèdres dont les faces sont toutes les cases: si faces coplanaires ne sont pas autorisés, même se ils sont déconnectés, il ya seulement le cube. Sinon, il est aussi le résultat de coller six cubes aux côtés de l'un, tous les sept de la même taille; il a 30 faces carrées (en comptant visages déconnectés dans le même plan que séparée). Cela peut être prolongée dans une, deux ou trois directions: nous pouvons considérer l'union des arbitrairement de nombreuses copies de ces structures, obtenus par des traductions (exprimée en tailles de cube) (2,0,0), (0,2,0 ) et / ou (0,0,2), d'où chaque paire adjacente ayant une cube commun. Le résultat peut être tout ensemble connexe de cubes avec des positions (a, b, c), avec des nombres entiers a, b, c dont au plus un est encore.
- Il ya pas de nom particulier pour les polyèdres dont les faces sont tous des pentagones ou pentagrammes équilatéraux. Il ya infiniment beaucoup d'entre eux, mais un seul est convexe: le dodécaèdre. Le reste sont assemblés par collage) (combinaisons des polyèdres réguliers décrit précédemment: le dodécaèdre, le petit dodécaèdre étoilé, le grand dodécaèdre étoilé et le grand icosaèdre.
Il ne existe pas polyèdre dont les faces sont tous identiques et sont des polygones réguliers avec six côtés ou plus parce que le sommet de trois hexagones réguliers définit un plan. (Voir infinie polyèdre biais des exceptions avec zigzaguant chiffres sommet.)
Deltaèdres
Un deltaèdre (deltaèdres pluriel) est un polyèdre dont les faces sont tous les triangles équilatéraux. Il ya une infinité de deltaèdres, mais seulement huit d'entre eux sont convexes:
- 3 polyèdres réguliers convexes (3 des solides de Platon)
- 5 non uniforme polyèdres convexes (5 des solides de Johnson)
- Dipyramid triangulaire
- Dipyramid pentagonale
- Disphénoïde adouci
- Prisme triangulaire triaugmenté
- Dipyramid carré Gyroelongated
Solides de Johnson
Norman Johnson recherchée qui polyèdres non uniforme avait visages réguliers. En 1966 , il a publié une liste de 92 solides convexes, maintenant connu sous le nom Solides de Johnson, et leur ont donné leurs noms et numéros. Il n'a pas prouvé qu'il y avait seulement 92, mais il a fait des conjectures qu'il n'y avait pas d'autres. Victor Zalgaller en 1969 se est avéré que la liste de Johnson était complète.
D'autres familles importantes de polyèdres
Pyramides
Pyramides comprennent certains des plus séculaire et célèbre de tous les polyèdres.
Stellations et facettings
 |  |  |  | | |  |
Stellation d'un polyèdre est le processus d'extension des faces (dans leurs plans) afin qu'ils se rencontrent pour former un nouveau polyèdre.
Ce est la réciproque exacte du processus de facettage qui est le processus d'enlever des parties d'un polyèdre sans créer de nouveaux sommets.
Zonoèdres
Un zonoèdre est un polyèdre convexe où chaque visage est un polygone avec inversion symétrie ou, de façon équivalente, en vertu de la symétrie des rotations de 180 °.
Composés
Composés polyédriques sont formées en tant que composés de deux ou plusieurs polyèdres.
Ces composés partagent souvent les mêmes sommets que les autres polyèdres et sont souvent formées par constellation. Certains sont énumérés dans le liste des modèles polyèdre Wenninger.
Orthogonal Polyhedra
Un polyèdre est une orthogonal dont toutes les faces se rencontrent à angle droit, et dont toutes les arêtes sont parallèles aux axes d'un système de coordonnées cartésiennes. Mis à part une boîte rectangulaire, polyèdres orthogonaux sont non convexe. Ils sont les analogues de 2D en 3D polygones orthogonaux (également connus sous le nom polygones rectilignes). Polyèdres orthogonaux sont utilisés dans géométrie algorithmique, où leur structure contraint a permis des avancées sur les problèmes non résolus pour les polyèdres arbitraires, par exemple, se déroule la surface d'un polyèdre à un net (polyèdre).
Les généralisations de polyèdres
Le nom 'polyèdre' est venu à être utilisé pour une variété d'objets ayant des propriétés structurales similaires à polyèdres traditionnelle.
Apeirohedra
Une surface polyédrique classique comprend finie, régions planes délimitées, rejoint par paires le long des bords. Si une telle surface se étend indéfiniment, il est appelé un apeirohedron. Les exemples incluent:
- Pavages ou pavages du plan.
- structures éponge appelés infinie polyèdres biais.
Voir aussi: Apeirogon - infinie polygone régulier: {∞}
Polyèdres Complexe
Un polyèdre est un complexe qui est construit 3-espace unitaire. Cet espace dispose de six dimensions: trois vrais correspondant à l'espace ordinaire, avec chacun accompagné d'une dimension imaginaire. Voir, par exemple Coxeter (1974).
Polyèdres incurvée
Certains domaines d'études permettra polyèdres d'avoir des visages et des bords incurvés.
Polyèdres sphériques
La surface d'une sphère peut être divisée en segments de ligne dans des régions limitées, pour former un polyèdre sphérique. Une grande partie de la théorie des polyèdres symétrique est le plus commodément dérivé de cette manière.
Polyèdres sphériques ont une histoire longue et respectable:
- Les premiers polyèdres artificiels connus sont polyèdres sphériques sculpté dans la pierre.
- Poinsot utilisé polyèdres sphériques de découvrir les quatre polyèdres réguliers étoiles.
- Coxeter les a utilisés pour énumérer tous, mais l'un des polyèdres uniformes.
Certains polyèdres, comme hosohedra, exister que comme polyèdres sphériques et ont pas d'analogue à face plate.
Curved spacefilling polyèdres
Deux types importants sont:
- Bulles dans mousses et mousses.
- Spacefilling formulaires utilisés dans l'architecture. Voir, par exemple Pearce (1978).
Plus besoin d'être dit à propos de ceux-ci, aussi.
Polyèdres général
Plus récemment mathématiques a défini un polyèdre comme un ensemble en réel affine (ou euclidienne ) de tout l'espace à n dimensions dont les côtés plats. Il pourrait être défini comme l'union d'un nombre fini de polyèdres convexes, où un polyèdre convexe est un ensemble qui est l'intersection d'un nombre fini de demi-espaces. Il peut être limitée ou illimitée. Dans ce sens, un polytope est un polyèdre borné.
Tous les polyèdres traditionnels sont des polyèdres général, et en plus il ya des exemples comme:
- Un secteur circulaire dans le plan. Par exemple, la région du plan cartésien constitué de tous les points au-dessus de l'axe horizontal et à la droite de l'axe vertical: {(x, y): x ≥ 0, y ≥ 0}. Ses côtés sont les deux axes positifs.
- Un octant en 3-espace euclidien, {(x, y, z): x ≥ 0, y ≥ 0, z ≥ 0}.
- Un prisme de mesure infinie. Par exemple, un prisme carré doublement infini en 3-espace, formé d'un carré dans le Plane xy balayé le long de l'axe z: {(x, y, z): 0 ≤ x ≤ 1, 0 ≤ y ≤ 1} .
- Chaque cellule dans une Tessellation de Voronoï est un polyèdre convexe. Dans la mosaïque de Voronoi d'un ensemble S, la cellule A correspondant à un point c ∈ S est délimitée (d'où un polyèdre traditionnel) lorsque c se situe dans la intérieur de la enveloppe convexe de S, et le cas contraire (lorsqu'il se trouve sur le c limite de la coque convexe de S) A est illimitée.
Polyèdres face ou squelettique creuse
Il ne est pas nécessaire de remplir le visage d'un personnage avant que nous puissions l'appeler un polyèdre. Par exemple Leonardo da Vinci a conçu des modèles de cadre des solides réguliers, dont il a dessiné pour Le livre de Pacioli Divina Proportione. Dans les temps modernes, Branko Grünbaum (1994) a fait une étude spéciale de cette classe de polyèdres, dans lequel il a développé une idée précoce des polyèdres abstrait. Il a défini un visage comme un ensemble ordonné de sommets de manière cyclique, et a permis faces à biaiser ainsi que plane.
Tessellations ou pavages
Tessellations ou pavages du plan sont parfois traités comme des polyèdres, parce qu'ils ont beaucoup en commun. Par exemple les réguliers peuvent être donnés Symboles Schläfli.
Polyèdres non-géométrique
Diverses constructions mathématiques ont été trouvés comme ayant des propriétés aussi présents dans polyèdres traditionnelle.
Polyèdres topologique
Un polytope topologique est un espace topologique donnée avec une décomposition spécifique dans des formes qui sont topologiquement équivalent à polytopes convexes et qui sont attachés les uns aux autres d'une manière régulière.
Un tel chiffre est appelé simplicial si chacune de ses régions est une simplex, ce est à dire dans un espace de dimension n chaque région a une n sommets. Le double d'un polytope simplicial est appelé simple. De même, une classe largement étudié des polytopes (polyèdres) est celle de polyèdres cubique, lorsque le bloc de construction de base est un cube de dimension n.
Résumé polyèdres
Un résumé est un polyèdre partiellement ordonné set (ensemble ordonné) des éléments. Les théories diffèrent dans les détails, mais essentiellement les éléments de l'ensemble correspondent au corps, faces, arêtes et sommets du polyèdre. L'ensemble vide correspond au polytope nulle ou nullitope, qui a une dimension de -1. Ces posets appartiennent à la grande famille des polytopes abstraits dans un certain nombre de dimensions.
Polyèdres sous forme de graphiques
Tout polyèdre donne lieu à une graphique, ou squelette, avec des sommets et arêtes correspondantes. Ainsi terminologie et les propriétés graphique peuvent être appliqués à des polyèdres. Par exemple:
- En raison de Steinitz théorème de polyèdres convexes sont en correspondance un-à-un avec graphes planaires 3-connexes.
- Le tétraèdre donne lieu à une graphe complet (K 4). Ce est le seul polyèdre de le faire.
- L' octaèdre donne lieu à une fortement graphe régulier, parce sommets adjacents ont toujours deux communes voisines, et sommets non adjacents ont quatre.
- Le Solides d'Archimède donnent lieu à graphiques réguliers: sept des solides d'Archimède sont des degré 3, 4 de degré 4, et le reste sont deux paires chirales de degré 5.
Histoire
Préhistoire
Pierres taillées dans des formes montrant les symétries de divers polyèdres ont été trouvés dans l'Ecosse et peuvent être autant âgé de 4000 ans. Ces pierres montrent non seulement la forme de divers polyehdra symétrique, mais aussi les relations de la dualité entre certains d'entre eux (ce est que les centres des faces du cube donne les sommets d'un octaèdre, et ainsi de suite). Des exemples de ces pierres sont exposées dans le Chambre John Evans de la Ashmolean Museum à Oxford University . Il est impossible de savoir pourquoi ces objets ont été faites, ou comment le sculpteur a gagné l'inspiration pour eux.
Autres polyèdres ont bien sûr fait leur marque dans l'architecture - des cubes et des parallélépipèdes étant des exemples évidents, avec les pyramides premiers à quatre côtés de l'ancienne Egypte aussi datant de l'âge de pierre.
Le Étrusques ont précédé les Grecs dans leur prise de conscience de certains au moins des polyèdres réguliers, comme en témoigne la découverte près Padoue (dans le nord de l'Italie ) à la fin des années 1800 d'un dodécaèdre constitué de stéatite, et datant de plus de 2500 années (Lindemann, 1987). Pyritohedric cristaux se trouvent dans le nord de l'Italie.
Grecs
Les premiers enregistrements connus écrites de ces formes proviennent de classiques grecs auteurs, qui ont également donné la description mathématique d'abord connu d'entre eux. Les premiers Grecs étaient intéressés principalement dans le polyèdres réguliers convexes, tandis que d'Archimède ensuite élargi son étude à la convexes polyèdres uniformes.
Musulmans et les Chinois
Après la fin de l'ère classique, savants islamiques ont continué à faire des progrès, par exemple dans le Xe siècle Abu'l Wafa décrit les polyèdres sphérique régulière et quasiregular convexe. Pendant ce temps en Chine, la dissection du cube dans son tétraèdre caractéristique (orthoscheme) et solides apparentés a été utilisé comme base pour le calcul des volumes de terre pour être déplacé lors de fouilles d'ingénierie.
Renaissance
Beaucoup à dire ici: Piero della Francesca, Pacioli, Léonard de Vinci, Wenzel Jamnitzer, Durer, etc. menant à Kepler.
Polyèdres étoiles
Pour près de 2000 ans, le concept d'un polyèdre était resté tel que développé par les anciens mathématiciens grecs.
Johannes Kepler est rendu compte que polygones étoilés pourraient être utilisés pour construire des polyèdres étoiles, qui ont polygones réguliers non convexes, typiquement pentagrammes que visages. Certains de ces polyèdres étoiles aient pu être découverts avant l'époque de Kepler, mais il était le premier à reconnaître qu'ils pourraient être considérés comme «ordinaire» si l'on levé la restriction qui polytopes réguliers être convexe. Plus tard, Louis Poinsot réalisé cette étoile chiffres vertex (circuits autour de chaque coin) peuvent également être utilisés, et ont découvert les deux polyèdres étoiles régulière restant. Cauchy a prouvé la liste complète Poinsot, et leur a donné Cayley leurs noms anglais acceptés: (Kepler) le petit dodécaèdre étoilé et grand dodécaèdre étoilé, et (Poinsot de) la grand icosaèdre et grand dodécaèdre. Collectivement, ils sont appelés les Polyèdres Kepler-Poinsot.
Les polyèdres de Kepler-Poinsot peut être construite à partir des solides de Platon par un processus appelé constellation. La plupart des constellations ne sont pas régulières. L'étude des constellations des solides de Platon a été donné une grande poussée par HSM Coxeter et d'autres en 1938, avec le désormais fameux papier Le 59 icosaèdres. Ce travail a récemment été re-publié (Coxeter, 1999).
Le processus réciproque aux constellation est appelée facettage (ou facettes). Chaque constellation d'un polytope est double, ou réciproque, dans une certaine facettage de la double polytope. Le polyèdres réguliers en étoile peut aussi être obtenue par facettage les solides de Platon. Pont 1974 a énuméré les facettings simples du dodécaèdre, et de leur réciproque de découvrir une stellation de l'icosaèdre qui manquait de la célèbre "59". Plus ont été découverts depuis, et l'histoire ne est pas encore terminé.
Voir aussi:
- Polyèdre régulier: Histoire
- Polytope régulier: Histoire de la découverte.
Polyhedra dans la nature
Pour des événements naturels de polyèdres réguliers, voir Polyèdre régulier: Histoire.
Polyèdres irréguliers apparaissent dans la nature comme des cristaux .
Livres sur polyèdres
Livres d'introduction, convient également pour un usage scolaire
- Cromwell, P .; Polyhedra, CUP hbk (1997), pbk. (1999).
- Cundy, HM & Rollett, AP; modèles mathématiques, 1ère éd. hbk OUP (1951), 2ème édition. hbk OUP (1961), 3e éd. pbk Tarquin (1981).
- Holden; Formes, l'espace et la symétrie, (1971), Dover pbk (1991).
- Pearce, P et Pearce, S: Polyhedra amorce, Van Nost. Reinhold (mai 1979), ISBN-10: 0442264968 ISBN-13: 978-0442264963.
- Tarquin publications: livres de découpe et font des modèles de cartes.
- Wenninger, les modèles M .; Polyhedron pour la salle de classe, pbk (1974)
- Wenninger, les modèles M .; Polyhedron, CUP hbk (1971), pbk (1974).
- Wenninger, sphérique modèles, CUP de M.
- Wenninger, double modèles, CUP de M.
Premier cycle
- Coxeter, HSM DuVal, Flather & Petrie; La cinquante-neuf icosaèdres, 3e éd. Tarquin.
- Coxeter, HSM Douze essais géométriques. Réédité comme La beauté de la géométrie, Dover.
- Thompson, Sir D'AW sur la croissance et la forme, (1943). (Ne sais pas si ce est la bonne catégorie pour celui-ci, je ne ai pas lu).
Design et architecture biais
- Critchlow, K .; ordre dans l'espace.
- Pearce, P .; Structure dans la nature est une stratégie pour la conception, le MIT (1978)
- Williams, R .; La fondation géométrique de la structure naturelle, Dover (1979).
Textes mathématiques avancées
- Coxeter, HSM; polytopes réguliers 3e éd. Dover (1973).
- Coxeter, HSM; polytopes complexes régulières, CUP (1974).
- Lakatos, Imre; Preuves et Réfutations, Cambridge University Press (1976) - la discussion de la preuve de caractéristique d'Euler
- Plusieurs de plus à ajouter ici.
Livres historiques
- Brückner, Vielecke und Vielflache (polygones et polyèdres), (1900).
- Fejes Toth, L .;