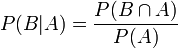Espace de probabilité

La définition de l'espace de probabilité est le fondement de la théorie des probabilités . Il a été introduit par Kolmogorov dans la 1930. Pour une alternative algébrique pour l'approche de Kolmogorov, voir algèbre des variables aléatoires.

Définition

Un espace de probabilité 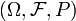est un mesure l'espace avec une mesure P qui satisfait la axiomes de probabilité.

L'espace de l'échantillon 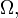est non vide ensemble dont les éléments sont connus comme les résultats ou les états de la nature et sont souvent donné le symbole 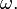L'ensemble de tous les résultats possibles d'une expérience est connu que l'espace de l'expérience de l'échantillon.

Événements

Le deuxième élément, 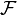, Est un σ-algèbre des sous-ensembles de 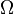. Ses éléments sont appelés événements, qui sont des ensembles de résultats pour lesquels on peut poser une probabilité.

Parce que 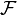est un σ-algèbre, il contient 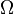; aussi, le complément de tout événement est un événement, et le syndicat de toute séquence (fini ou infini dénombrable) des événements est un événement.

Habituellement, les événements sont la Lebesgue-mesurable ou Borel-ensembles mesurables de nombres réels.

Mesure probabilité

La mesure de probabilité 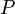est une fonction à partir de 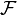pour les nombres réels qui attribue à chaque événement une probabilité comprise entre 0 et 1. Il doit satisfaire la axiomes de probabilité.

Parce que 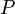est une fonction définie sur 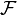et pas sur 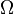, L'ensemble des événements ne est pas nécessaire d'être le complète régler la puissance de l'espace de l'échantillon; ce est pas tous ensemble de résultats est forcément un événement.

Lorsque plus d'une mesure est en cours de discussion, des mesures de probabilité sont souvent écrites en tableau noir gras pour les distinguer. Quand il ne est qu'une mesure de probabilité en cours de discussion, il est souvent désigné par le Pr, ce qui signifie "probabilité de".

Concepts associés

Distribution de probabilité

Toute distribution de probabilité définit une mesure de probabilité.

Variables aléatoires

Une variable aléatoire X est un fonction mesurable de l'espace de l'échantillon 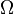; à un autre espace mesurable appelé l'espace d'état.

Si X est un valeur réelle variable aléatoire, alors la notation 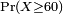est un raccourci pour 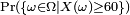, En admettant que 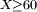est un événement.

Probabilité conditionnelle

La définition de Kolmogorov des espaces de probabilité donne naissance au concept naturel de probabilité conditionnelle. Chaque ensemble 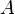avec probabilité non nulle (ce est-P (A) 0>) définit une autre mesure de probabilité

sur l'espace. Ce est généralement interprété comme la «probabilité de B Une donnée".

Indépendance

Deux événements A et B sont dits indépendant si P (A ∩ B) = P (A) P (B).

Deux variables aléatoires, X et Y, sont censés être indépendante si un événement défini en termes de X est indépendant de tout événement défini en termes de Y. Formellement, ils génèrent σ-algèbres indépendante, où deux σ-algèbres G et H, qui sont des sous-ensembles de F sont dites indépendantes si un élément de G est indépendante de tout élément de H.

Le concept d'indépendance est là que la théorie des probabilités quitte théorie de la mesure.

L'exclusivité mutuelle

Deux événements A et B sont dits mutuellement exclusives ou disjoints si P (A ∩ B) = 0. (Ceci est plus faible que A ∩ B = ∅, ce qui est la définition de disjoint pour les jeux).

Si A et B sont des événements disjoints, alors P (A ∪ B) = P (A) + P (B). Cela se étend à une séquence (fini ou infini dénombrable) des événements. Cependant, la probabilité de l'union d'un ensemble non dénombrable d'événements ne est pas la somme de leurs probabilités. Par exemple, si Z est une distribution normale variable aléatoire, alors P (Z = x) est de 0 pour tout x, mais P (Z est réel) = 1.

L'événement A ∩ B est désigné par A et B, et l'événement A ∪ B que A ou B.

Exemples

Premier exemple

Si l'espace concerne une chiquenaude d'un pièce de monnaie, puis les résultats sont têtes et les queues:

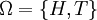
Les événements sont

• {} H: têtes,
• {T}: queues,
• {}: Ni têtes ni queues, et
• {H, T}: pile ou face.

Alors,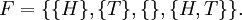

Il ya une chance de jeter soit tête ou la queue de cinquante pour cent: P ({H}) = P ({T}) = 0,5. La chance de jeter ne est nulle: P ({}) = 0, et la chance de jeter un ou l'autre est une: P ({H, T}) = 1.

Deuxième exemple

Si 100 électeurs doivent être tirés au hasard parmi tous les électeurs de la Californie et a demandé qui ils vont voter pour le gouverneur, alors l'ensemble de toutes les séquences de 100 votes californiens serait le Ω de l'espace de l'échantillon.

L'ensemble de toutes les séquences de 100 électeurs californiens dans laquelle au moins 60 vont voter pour Schwarzenegger est identifié avec «l'événement» qu'au moins 60 des 100 électeurs choisis allons donc voter.

Ensuite, 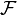contient: (1) l'ensemble de toutes les séquences de 100 où au moins 60 voix pour Schwarzenegger; (2) l'ensemble de toutes les séquences de 100 où moins de 60 voix pour Schwarzenegger (l'inverse de (1)); (3) l'espace Ω de l'échantillon comme ci-dessus; et (4) l'ensemble vide.

Un exemple d'une variable aléatoire est le nombre d'électeurs qui vont voter pour Schwarzenegger dans l'échantillon de 100.