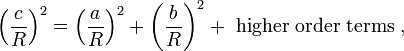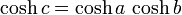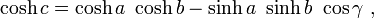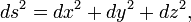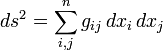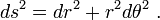Théorème de Pythagore
Contexte des écoles Wikipédia
SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
| Trigonométrie |
|---|
| Histoire Usage Fonctions Généralisé Fonctions inverses Pour en savoir plus |
| Référence |
| Identités Constantes précises Tables trigonométriques |
| Lois et théorèmes |
| Loi des sinus Loi des cosinus Loi des tangentes Loi de cotangentes Théorème de Pythagore |
| Calcul |
| Substitution trigonométrique Intégrales de fonctions Dérivées des fonctions Intégrales de fonctions inverses |
| Géométrie |
|---|
 Oxyrhynchus papyrus (P.Oxy. I 29) montrant fragment de Eléments d'Euclide |
| Histoire de la géométrie |
Branches La géométrie euclidienne · La géométrie non-euclidienne · géométrie analytique · Géométrie riemannienne · Géométrie différentielle · La géométrie projective · Géométrie algébrique |
Les domaines de recherche |
Concepts importants Remarque · Ligne · Perpendiculaire · Parallèlement · Le segment de ligne · Ray · Avion · Longueur · Espace · Volume · Vertex · Angle · Congruence · Similarité · Polygone · Triangle · Altitude · · Hypoténuse théorème de Pythagore · Quadrilatère · Trapèze · Kite · Parallélogramme ( Rhomboid, Rectangle, Rhombus, Place ) · Diagonal · Symétrie · Curve · Cercle · Zone d'un disque · Circonférence · Diamètre · Cylindre · Sphère · Pyramide · Dimensions ( une, deux, trois, quatre) |
Géomètres Aryabhata · Ahmès · Apolonius · Archimède · Baudhayana · Bolyai · Brahmagupta · Euclid · Pythagore · Khayyám · Descartes · Pascal · Euler · Gauss · Ibn al-Yasamin · Jyeṣṭhadeva · Kâtyâyana · Lobachevsky · Manava · Minggatu · Riemann · Klein · Parameshvara · Poincaré · Al-Sijzi · Hilbert · Minkowski · Cartan · Veblen · Sakabe Kōhan · Gromov · Atiyah · Virasena · Yang Hui · Yasuaki Aida · Zhang Heng |
En mathématiques , le théorème de Pythagore - ou le théorème de Pythagore - est une relation dans la géométrie euclidienne entre les trois côtés d'un triangle (triangle rectangle). En termes de secteurs, il déclare:
Dans tout triangle rectangle, la zone du carré dont le côté est de la hypoténuse (du côté opposé à l'angle droit) est égale à la somme des aires des carrés dont les côtés sont les deux branches (les deux côtés qui se rencontrent à un angle droit).
Le théorème peut être écrite comme une équation concernant les longueurs des côtés a, b et c, souvent appelée l'équation de Pythagore:
où c représente la longueur de l'hypoténuse et a et b représentent les longueurs des deux autres côtés.
Le théorème de Pythagore est nommé d'après le Mathématicien grec Pythagore (environ 570 BC-495 BC ca.), qui par tradition est crédité de sa découverte et la preuve , même se il est souvent avancé que la connaissance du théorème lui est antérieure. Il est prouvé que Mathématiciens babyloniens compris la formule, même se il ya peu de preuves de survivant qu'ils ont utilisé dans un cadre mathématique.
Le théorème a de nombreuses preuves , peut-être plus que tout autre théorème mathématique. Ce sont très divers, y compris les preuves géométriques et des preuves algébriques, avec certains datant de plusieurs milliers d'années. Le théorème peut être généralisé de diverses manières, y compris les espaces de dimensions supérieures, à des espaces qui ne sont pas euclidienne, à des objets qui ne sont pas triangles droit, et même, à des objets qui ne sont pas du tout des triangles, mais de dimension n solides. Le théorème de Pythagore a suscité l'intérêt en dehors des mathématiques comme un symbole de hermétisme mathématique, mystique, ou la puissance intellectuelle; références populaires de la littérature, des pièces de théâtre, des comédies musicales, des chansons, des timbres et des dessins animés abondent.
D'autres formes
Comme indiqué dans l'introduction, si c désigne la longueur de l'hypoténuse et a et b désignent les longueurs des deux autres côtés, le théorème de Pythagore peut être exprimée par l'équation de Pythagore:
Si la longueur de tous les deux a et b sont connus, alors c peut être calculée comme suit:
Si la longueur de l'hypoténuse c et une branche (A ou B) sont connus, alors la longueur de l'autre branche peut être calculé avec les équations suivantes:
ou
L'équation de Pythagore concerne les côtés d'un triangle rectangle d'une manière simple, de sorte que si les longueurs de toutes les deux parties sont connus de la longueur du troisième côté peut être trouvé. Un autre corollaire du théorème est que, dans tout triangle rectangle dont l'hypoténuse est supérieure à l'une quelconque des jambes, mais inférieur à la somme d'eux.
Une généralisation de ce théorème est le loi du cosinus, ce qui permet le calcul de la longueur du troisième côté d'un triangle, étant donné les longueurs des deux côtés et la grandeur de l'angle entre eux. Si l'angle entre les côtés est un angle droit, la loi des cosinus réduit à l'équation de Pythagore.
Preuves
Ce théorème peut avoir des preuves plus connus que tout autre (la loi de réciprocité quadratique étant un autre concurrent pour cette distinction); Le livre contient 370 Proposition de Pythagore preuves.
Preuve en utilisant triangles semblables
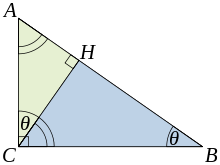
Cette démonstration est basée sur la proportionnalité des deux côtés de triangles semblables, ce est sur le fait que la rapport de deux des côtés correspondants des triangles semblables est le même quelle que soit la taille des triangles.
Soit ABC représente un triangle rectangle, avec l'angle droit situé à C, comme indiqué sur la figure. Nous attirons l' altitude du point C et H appel son intersection avec le côté AB. Le point H divise la longueur de l'hypoténuse c en parties d et e. Le nouveau ACH triangle est similaire à triangle ABC, parce qu'ils ont tous les deux un angle droit (par définition de l'altitude), et ils partagent l'angle en A, ce qui signifie que le troisième angle sera la même dans les deux triangles ainsi, marqués comme θ dans la figure. Par un raisonnement similaire, le triangle CBH est également semblable à ABC. La preuve de la similitude des triangles nécessite la Triangle postulat: la somme des angles d'un triangle est deux angles droits, et est équivalente à la postulat des parallèles. Similitude des triangles mène à l'égalité des ratios de côtés correspondants:
Le premier résultat correspond au cosinus de chaque angle θ de la seconde et le résultat correspond sinus.
Ces rapports peuvent être écrites comme:
La somme de ces deux égalités, nous obtenons
qui, rangements, est le théorème de Pythagore:
Le rôle de cette preuve dans l'histoire est l'objet de beaucoup de spéculations. La question sous-jacente est pourquoi Euclide n'a pas utilisé cette preuve, mais inventé une autre. Une hypothèse est que la preuve par des triangles semblables impliquait une théorie des proportions, un sujet pas discuté plus tard dans les éléments, et que la théorie des proportions nécessaire la poursuite du développement à l'époque.
La preuve d'Euclid
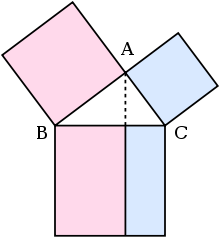
Dans les grandes lignes, voici comment la preuve dans d'Euclide Éléments le produit. Le grand carré est divisé en un rectangle gauche et à droite. Un triangle est construit qui a la moitié de la surface du rectangle gauche. Puis un autre triangle est construit qui a la moitié de la superficie de la place sur le côté le plus à gauche. Ces deux triangles sont présentés pour être en harmonie, ce qui prouve cette place a la même zone que le rectangle gauche. Cet argument est suivi par une version similaire pour le droit rectangle et la place restante. Rassembler les deux rectangles de réformer le carré de l'hypoténuse, sa superficie est la même que la somme de la surface des deux autres places. Les détails sont à côté.
Soit A, B, C soit le sommets d'un triangle rectangle, avec un angle droit en A. Tracer une perpendiculaire de A sur le côté opposé à l'hypoténuse dans le carré de l'hypoténuse. Cette ligne divise le carré de l'hypoténuse en deux rectangles, chacun ayant le même secteur que l'une des deux places sur les jambes.
Pour la preuve formelle, nous avons besoin de quatre élémentaire lemmes:
- Si deux triangles ont deux côtés de l'une égale à deux côtés de l'autre, chacun à chacun, et les angles inclus par les côtés égaux, alors les triangles sont congruents ( côté-angle-côté).
- L'aire d'un triangle est la moitié de la superficie d'un parallélogramme sur la même base et ayant la même altitude.
- L'aire d'un rectangle est égal au produit de deux côtés adjacents.
- L'aire d'un carré est égal au produit de deux de ses côtés (suit de trois).
Ensuite, chaque carré supérieur est liée à une harmonie de triangle avec un autre triangle liée à son tour à l'un des deux rectangles qui composent le carré inférieur.
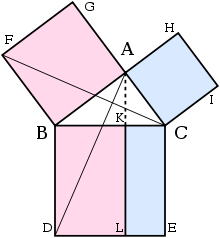
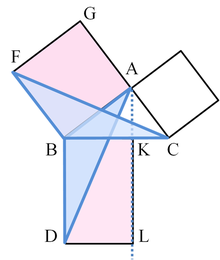
La preuve est la suivante:
- Laissez ACB un triangle rectangle dont l'angle droit CAB.
- Sur chacun des côtés BC, AB, et CA, carrés sont dessinés, CBDE, BAGF et ACIH, dans cet ordre. La construction nécessite des carrés des théorèmes immédiatement précédent dans Euclide, et dépend du postulat parallèle.
- De A, tracer une ligne parallèle à BD et CE. Il se croisent perpendiculairement BC et DE au K et L, respectivement.
- Rejoignez FC et AD, pour former le BCF triangles et BDA.
- Angles CAB et le sac sont deux angles droits; par conséquent, C, A, et G sont colinéaires . De même pour B, A et H.
- Angles CDB et FBA sont deux angles droits; donc l'angle ABD est égale à l'angle FBC, puisque les deux sont la somme d'un angle droit et l'angle ABC.
- Puisque AB est égale à FB et BD est égale à BC, triangle ABD doit être congru à triangle FBC.
- Depuis AKL est une ligne droite, parallèle à BD, puis rectangle BDLK a deux fois l'aire du triangle ABD parce qu'ils part la base BD et ont la même altitude BK, ce est à dire, une ligne normale à leur base commune, reliant les lignes parallèles et BD AL. (Lemme 2)
- Puisque C est colinéaire avec A et G, BAGF carré doit être deux fois dans la zone du triangle FBC.
- Par conséquent BDLK rectangle doit avoir la même zone que BAGF carré = 2 AB.
- De même, il peut être démontré que rectangle CKLE doit avoir la même zone que carré ACIH = AC 2.
- L'ajout de ces deux résultats, AB 2 + 2 = AC BD × BK + KL × KC
- Depuis BD = KL, BD × BK + KL × KC = BD (BK + KC) = BD × BC
- Par conséquent AB 2 + 2 = AC 2 Colombie-Britannique, depuis CBDE est un carré.
Cette preuve, qui apparaît dans les Eléments d'Euclide que celui de la Proposition 47 dans le Livre 1, démontre que la région de la carré de l'hypoténuse est la somme des surfaces des deux autres places. Ce est tout à fait distincte de la preuve par la similitude des triangles, qui est conjecturé être la preuve que Pythagore utilisé.
Preuve par réarrangement
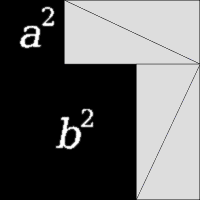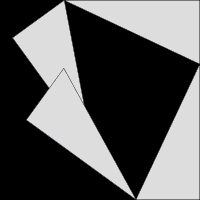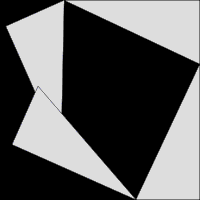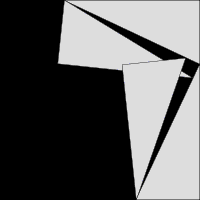
L'animation de gauche se compose d'un grand carré, côté a + b, contenant quatre triangles rectangles identiques. Les triangles sont présentés dans deux accords, le premier de ce qui laisse deux places a 2 et b 2 soient découvertes, dont la seconde feuilles c carré 2 découvert. La zone couverte par le carré extérieur ne change jamais, et la région des quatre triangles est le même au début et à la fin, pour que les zones noires carrés doit être égal, donc 2 + b 2 = c 2.
Une seconde preuve est donnée par l'animation du milieu. Une grande place est formé avec coin c 2, à partir de quatre triangles rectangles identiques avec des côtés a, b et c, équipés autour d'une petite place centrale. Ensuite, deux rectangles sont formés avec des côtés a et b en déplaçant les triangles. Alliant le petit carré avec ces rectangles produit deux carrés de zones A 2 et B 2, qui doivent avoir la même zone que la grande place initiale.
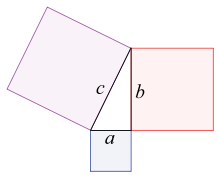
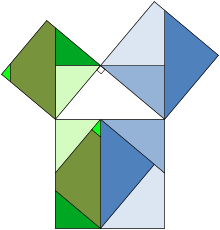
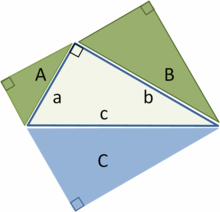
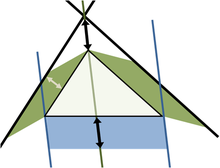
La troisième, l'image la plus à droite donne également une preuve. Les deux carrés supérieurs sont divisés comme le montre l'ombrage bleu et vert, en morceaux que lorsque réarrangé peut être faite pour se adapter sur la place inférieure sur l'hypoténuse - ou inversement la grande place peut être divisé comme indiqué en morceaux qui remplissent les deux autres . Cela montre la zone du grand carré est égale à celle des deux plus petits.
 |  |  |
Preuves algébriques
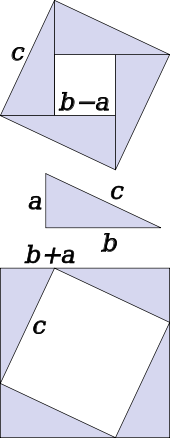
Le théorème peut être prouvé en utilisant algébriquement quatre exemplaires d'un triangle rectangle de côtés a, b et c, disposés à l'intérieur d'un carré de côté c comme dans la moitié supérieure du diagramme. Les triangles sont semblables avec coin 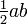 , Tandis que la petite place a côté b - a et environs (b - a) 2. La zone de la grande place est donc
, Tandis que la petite place a côté b - a et environs (b - a) 2. La zone de la grande place est donc
Mais ce est un carré de côté c et c la zone 2, de sorte
Une preuve similaire utilise quatre copies du même triangle disposés symétriquement autour d'un carré de côté c, comme représenté sur la partie inférieure du diagramme. Il en résulte un grand carré, de côté a + b et environs (a + b) 2. Les quatre triangles et le côté carré c doivent avoir la même surface que le carré plus grand,
donnant
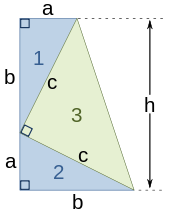
Une preuve connexe a été publié par l'ancien président américain James A. Garfield . Au lieu d'un carré, il utilise un trapèze, qui peut être construit à partir de la place dans la seconde des preuves ci-dessus en coupant en deux le long d'une diagonale du carré intérieur, pour donner le trapèze comme indiqué dans le schéma. Le aire du trapèze peut être calculée comme étant la moitié de l'aire du carré, ce est-
Le carré intérieur est de même diminué de moitié, et il ya seulement deux triangles de sorte que la preuve se déroule comme précédemment, sauf pour un facteur de  , Qui est enlevée en multipliant par deux pour obtenir le résultat.
, Qui est enlevée en multipliant par deux pour obtenir le résultat.
Preuve en utilisant les écarts
On peut arriver au théorème de Pythagore en étudiant comment les changements dans un côté produisent un changement de l'hypoténuse et employant calcul .
Le triangle ABC est un triangle rectangle, comme représenté sur la partie supérieure du diagramme, BC avec l'hypoténuse. En même temps, les longueurs sont mesurées en triangle comme représenté, avec l'hypoténuse de longueur y, le côté AC de longueur x et le côté AB de longueur a, comme on le voit dans la partie inférieure du diagramme.
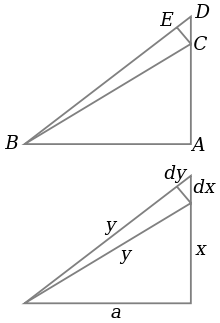
Si x est augmenté d'une petite quantité dx en étendant le côté AC légèrement à D, alors y augmente également par dy. Ces forment deux côtés d'un triangle, CDE, qui (avec E choisi de manière CE est perpendiculaire à l'hypoténuse) est un triangle rectangle approximativement similaire à ABC. Par conséquent, les rapports de leurs côtés doivent être les mêmes, à savoir:
Ce peut être réécrite comme suit:
Il se agit d'une équation différentielle qui est résolu pour donner
Et la constante peut être déduite à partir de x = 0, y = A pour donner l'équation
Ce est plus d'une preuve intuitive que formel: elle peut être rendue plus rigoureuse si les limites appropriées sont utilisées à la place de dx et dy.
Inverse
La converse du théorème est également vrai:
Pour toutes les trois nombres positifs a, b, et c tel que a 2 + b 2 = c 2, il existe un triangle avec des côtés a, b et c, et par exemple chaque triangle a un angle droit entre les côtés de longueur a et b .
Une déclaration alternative est:
Pour tout triangle dont les côtés a, b, c, si un 2 + b 2 = c 2, alors l'angle entre a et b mesure 90 °.
Ce inverse apparaît également dans Elements (livre I, de la Proposition 48) d'Euclide:
"Si dans un triangle de la place sur l'un des côtés est égale à la somme des carrés des deux autres côtés du triangle, l'angle contenue par les deux autres côtés du triangle est à droite."
Il peut être prouvé en utilisant la loi des cosinus ou comme suit:
Soit ABC un triangle dont les côtés mesurent a, b, c, avec un 2 + b 2 = c 2. Construire un second triangle avec des côtés de longueur a et b contenant un angle droit. D'après le théorème de Pythagore, il se ensuit que l'hypoténuse de ce triangle a une longueur c = √ a 2 + b 2, le même que l'hypoténuse du premier triangle. Étant donné que les côtés des deux triangles sont les mêmes longueurs a, b et c, les triangles sont congruents et doit avoir les mêmes angles. Par conséquent, l'angle entre le côté de longueur a et b dans le triangle original est un angle droit.
La preuve de l'inverse ci-dessus utilise le théorème de Pythagore lui-même. L'inverse peut également être prouvée sans assumer le théorème de Pythagore.
Un corollaire de la réciproque du théorème de Pythagore est un moyen simple de déterminer si un triangle est, obtus, ou aiguë, comme suit. Soit C choisie pour être la plus longue des trois côtés et a + b> c (sinon il n'y a pas de triangle en fonction de la inégalité du triangle). Les énoncés suivants se appliquent:
- Si un 2 + b 2 = c 2, le triangle est à droite.
- Si un 2 + b 2> c 2, le triangle est aiguë.
- Si a 2 + b 2 <c 2, alors le triangle est obtus.
Edsger Dijkstra a déclaré cette proposition sur les triangles aigus, à droite, et obtus dans cette langue:
- sgn (α + β - γ) = sgn (a 2 + b 2 - C 2),
où α est l'angle opposé au côté a, β est l'angle opposé au côté b, γ est l'angle opposé au côté c, et sgn est la fonction signer.
Conséquences et utilisations du théorème
Triplets pythagoriciens
Un Pythagore triple a trois entiers positifs a, b, et c, de sorte que a 2 + b 2 = c 2. En d'autres termes, un triplet de Pythagore représente les longueurs des côtés d'un triangle rectangle où les trois côtés ont des longueurs entières. Preuve de monuments mégalithiques en Europe du Nord montre que ces triples étaient connues avant la découverte de l'écriture. Cette triple est couramment écrite (a, b, c). Des exemples bien connus sont (3, 4, 5) et (5, 12, 13).
Une primitive de Pythagore triple est celui dans lequel a, b et c sont premiers entre eux (le plus grand commun diviseur de a, b et c est égal à 1).
Ce qui suit est une liste de triplets pythagoriciens primitive avec des valeurs inférieures à 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12 , 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77 , 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Longueurs incommensurables
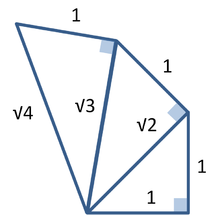
L'une des conséquences du théorème de Pythagore est que les segments de ligne dont les longueurs sont incommensurable (de sorte que le rapport de ce qui ne est pas un nombre rationnel ) peut être construit en utilisant une règle et un compas . Le théorème de Pythagore permet la construction de longueurs incommensurables parce que l'hypoténuse d'un triangle est lié aux côtés par la racine carrée opération.
La figure de droite montre comment construire des segments de ligne dont les longueurs sont dans le rapport de la racine carrée d'un nombre entier positif. Chaque triangle a un côté (marqué "1") qui est l'unité de mesure choisie. Dans chaque triangle rectangle, le théorème de Pythagore établit la longueur de l'hypoténuse en termes de cet appareil. Si une hypoténuse est liée à l'unité par la racine carrée d'un nombre entier positif qui ne est pas un carré parfait, ce est une réalisation d'une longueur incommensurable avec l'unité, tels que √ 2, 3 √, √ 5. Pour plus de détails, voir Quadratique irrationnel.
Longueurs incommensurables en conflit avec le concept de l'école pythagoricienne des nombres que seuls les nombres entiers. L'école pythagoricienne traitée proportions en comparaison des multiples entiers d'une sous-unité commune. Selon une légende, Hippasus de Métaponte (environ 470 BC) a été noyé en mer pour faire connaître l'existence de l'irrationnel ou incommensurables.
Les nombres complexes
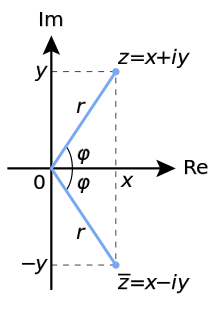
Pour tout nombre complexe
la valeur absolue ou module est donnée par
Ainsi, les trois quantités, r, x et y sont liées par l'équation de Pythagore,
Notez que r est défini comme étant un nombre positif ou zéro, mais x et y peut être aussi bien négative que positive. R est la distance géométrique de la z de zéro ou de l'origine O dans le plan complexe .
Ceci peut être généralisé pour trouver la distance entre deux points, Z 1 et Z 2 dire. La distance requise est donnée par
ils sont de nouveau reliés par une version de l'équation de Pythagore,
Distance euclidienne dans différents systèmes de coordonnées
La formule de distance en coordonnées cartésiennes est dérivé du théorème de Pythagore. Si (x 1, y 1) et (x 2, y 2) sont des points dans le plan, la distance entre eux, aussi appelé le Distance euclidienne, est donnée par
Plus généralement, dans euclidienne n -space , la distance euclidienne entre les deux points, 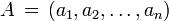 et
et 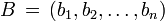 , Est défini, par la généralisation du théorème de Pythagore, que:
, Est défini, par la généralisation du théorème de Pythagore, que:
Si les coordonnées cartésiennes sont pas utilisés, par exemple, si les coordonnées polaires sont utilisés dans deux dimensions ou, en termes plus généraux, si Les coordonnées curvilignes sont utilisés, les formules exprimant la distance euclidienne est plus compliqué que le théorème de Pythagore, mais peuvent en être déduits. Un exemple typique où la distance en ligne droite entre deux points est converti en coordonnées curvilignes peut être trouvé dans le applications de polynômes de Legendre en physique. Les formules peuvent être découvertes en utilisant le théorème de Pythagore avec les équations relatives aux coordonnées curvilignes aux coordonnées cartésiennes. Par exemple, les coordonnées polaires (r, θ) peuvent être introduits en tant que:
Ensuite, deux points avec les emplacements (r 1, θ 1) et (2 r, θ 2) sont séparés par une distance s:
Effectuer les places et combiner les termes, la formule de Pythagore pour la distance en coordonnées cartésiennes produit la séparation en coordonnées polaires que:
en utilisant le trigonométrique produit-à-somme formules. Cette formule est la loi des cosinus , parfois appelé le théorème de Pythagore généralisé. De ce résultat, pour le cas où les rayons aux deux endroits sont à angle droit, l'angle fermé Δ θ = π / 2, et le formulaire correspondant au théorème de Pythagore est repris: 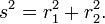 Le théorème de Pythagore, valable pour triangles rectangles, est donc un cas particulier de la loi plus générale de cosinus, valable pour triangles arbitraires.
Le théorème de Pythagore, valable pour triangles rectangles, est donc un cas particulier de la loi plus générale de cosinus, valable pour triangles arbitraires.
Identité trigonométrique de Pythagore
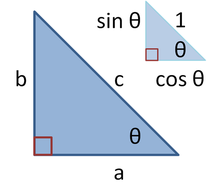
Dans un triangle rectangle de côtés a, b et c hypoténuse, la trigonométrie détermine la sinus et cosinus de l'angle θ entre un côté et l'hypoténuse que:
De ce qui suit:
où la dernière étape se applique le théorème de Pythagore. Cette relation entre sinus et cosinus est parfois appelée l'identité trigonométrique Pythagore fondamentale. Dans triangles semblables, les rapports des côtés sont les mêmes quelle que soit la taille des triangles, et dépendent des angles. Par conséquent, dans la figure, le triangle avec hypoténuse taille de l'unité a côté opposé de la taille et le péché θ côté adjacent du cos θ de taille en unités de l'hypoténuse.
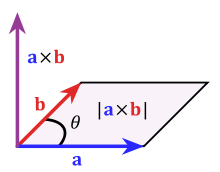
Relation avec le produit croisé
Le théorème de Pythagore concerne le produit en croix et produit scalaire d'une manière similaire:
Ceci peut être vu à partir de la définition du produit et le produit scalaire transversale, comme
avec n un vecteur unitaire perpendiculaire à la fois a et b. La relation résulte de ces définitions et l'identité trigonométrique de Pythagore.
Ceci peut également être utilisé pour définir le produit vectoriel. En réarrangeant l'équation suivante est obtenue
Cela peut être considéré comme une condition sur le produit croisé et de sorte qu'une partie de sa définition, par exemple en sept dimensions.
Généralisations
Des chiffres similaires sur les trois côtés
Une généralisation du théorème de Pythagore se étendant au-delà des zones de places sur les trois côtés pour chiffres similaires ont été connus par Hippocrate de Chios dans le cinquième siècle avant notre ère, et a été inclus par Euclide dans ses Éléments :
Si l'on érige des chiffres similaires (voir la géométrie euclidienne ) avec des côtés correspondants sur les côtés d'un triangle rectangle, la somme des aires des uns sur les deux petits côtés est égale à la zone de l'une sur le côté plus grand.
Cette extension suppose que les côtés du triangle d'origine sont les côtés correspondants des trois figures congruentes (donc les des rapports communs de côtés entre les chiffres similaires sont a: b:. C Bien que la preuve d'Euclide ne se appliquait qu'aux polygones convexes, le théorème se applique également aux polygones concaves et même à des chiffres similaires qui ont courbes limites (mais toujours avec une partie de la frontière d'un chiffre étant le côté du triangle d'origine).
L'idée de base derrière cette généralisation est que la zone d'une figure plane est proportionnelle au carré de la plus grande dimension linéaire, et en particulier est proportionnelle au carré de la longueur de tout côté. Ainsi, si les chiffres similaires avec des zones A, B et C sont érigés sur les côtés avec des longueurs correspondant a, b et c, puis:
Mais, par le théorème de Pythagore, a 2 + b 2 = c 2, de sorte que A + B = C.
Inversement, si nous pouvons prouver que A + B = C pendant trois chiffres similaires sans utiliser le théorème de Pythagore, alors nous pouvons travailler à rebours pour construire une démonstration du théorème. Par exemple, le centre triangle de départ peut être répliqué et utilisé comme un triangle C sur son hypoténuse, et deux triangles rectangles semblables (A et B) construits sur les deux autres côtés, formé en divisant le triangle central par son d'altitude. La somme des aires des deux triangles plus petits est donc celui de la troisième, ainsi A + B = C et en inversant la logique ci-dessus conduit à le théorème de Pythagore a 2 + b 2 = c 2.
Loi des cosinus
Le théorème de Pythagore est un cas particulier du théorème plus général concernant les longueurs des côtés dans un triangle quelconque, la loi des cosinus:
où θ est l'angle entre les côtés a et b.
Lorsque θ est de 90 degrés, puis cos θ = 0, et la formule se réduit à le théorème de Pythagore habitude.
Triangle arbitraire
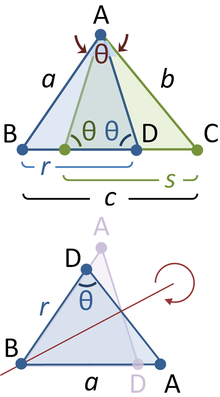
A ne importe quel angle sélectionné générale d'un triangle de côtés a, b, c, inscrire un triangle isocèle de telle sorte que les angles égaux à sa θ de base sont les mêmes que l'angle sélectionné. Supposons que le θ angle choisi est opposé au côté marqué c. L'inscription isocèle formes de triangle triangle ABD avec un côté opposé de l'angle et avec r latérale le long c. Un second triangle est formé avec le côté opposé de l'angle b et un côté de longueur le long de c, comme représenté sur la figure. Tabit ibn Qorra a déclaré que les côtés des trois triangles ont été liés comme:
Lorsque l'angle θ se approche de π / 2, la base du triangle isocèle se rétrécit, et r et s des longueurs se chevauchent de moins en moins. Lorsque θ = π / 2, la BAD devient un droit triangle, R + S = c, et le théorème de Pythagore originale est rétablie.
Une preuve observe que le triangle ABC a les mêmes angles que triangle ABD, mais dans l'ordre inverse. (Les deux triangles part l'angle au sommet B, les deux contiennent l'angle θ, et ont donc également le même troisième angle par le triangle postulat.) Par conséquent, ABC est similaire à la réflexion des ABD, le DBA de triangle dans le panneau inférieur. En prenant le rapport des côtés opposés et adjacents à θ,
De même, pour la réflexion de l'autre triangle,
Effacement de fractions et de l'ajout de ces deux relations:
le résultat requis.
Triangles générales utilisant parallélogrammes
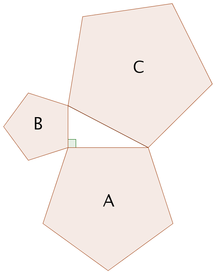
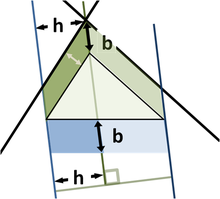
Une autre généralisation se applique à triangles qui ne sont pas des triangles rectangles, en utilisant parallélogrammes sur les trois côtés en place de carrés. (Squares sont un cas particulier, bien sûr). La figure du haut montre que pour un triangle scalène, l'aire du parallélogramme sur le côté le plus long est la somme des aires des parallélogrammes sur les deux autres côtés, à condition que le parallélogramme sur la côté long est construit comme indiqué (les dimensions marquées avec des flèches sont les mêmes, et déterminer les côtés du parallélogramme bas). Ce remplacement des carrés avec des parallélogrammes ressemble clairement au théorème de Pythagore 'origine, et a été considéré comme une généralisation par Pappus d'Alexandrie en 4 AD
Le chiffre inférieur indique les éléments de la preuve. Concentrez-vous sur le côté gauche de la figure. Le parallélogramme verte de gauche a la même zone que la gauche, partie bleue du parallélogramme bas car les deux ont la même base b et de hauteur h. Cependant, le parallélogramme vert gauche a également la même surface que le parallélogramme vert à gauche de la figure du haut, car ils ont la même base (le côté supérieur gauche du triangle) et la même hauteur normale de ce côté du triangle. Répétition de l'argument en faveur de la droite de la figure, le parallélogramme inférieur a le même secteur que la somme des deux parallélogrammes verts.
Solid Geometry
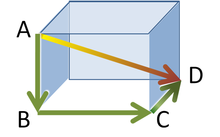
En termes de géométrie dans l'espace, le théorème de Pythagore peut être appliquée à trois dimensions suivantes. Considérons un solide rectangulaire comme indiqué sur la figure. La longueur de la diagonale BD se trouve de le théorème de Pythagore que:
où ces trois côtés forment un triangle rectangle. Utilisation diagonale BD horizontal et du bord vertical AB, la longueur de diagonale AD est ensuite trouvée par une seconde application du théorème de Pythagore que:
ou, tout faire en une seule étape:
Ce résultat est l'expression tridimensionnel de l'amplitude d'un vecteur v (la diagonale AD) en fonction de ses composantes orthogonales {v k} (les trois côtés mutuellement perpendiculaires):
Cette formulation en une seule étape peut être considérée comme une généralisation du théorème de Pythagore à des dimensions supérieures. Toutefois, ce résultat est vraiment juste l'application répétée du théorème de Pythagore origine à une succession de triangles rectangles dans une séquence de plans orthogonaux.
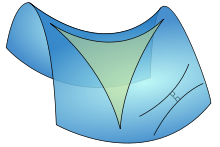
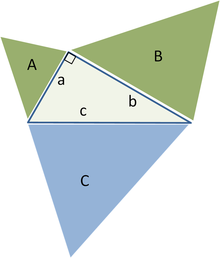
Une généralisation importante du théorème de Pythagore pour trois dimensions est Théorème de Gua, du nom de Jean-Paul de Gua de Malves: Si un tétraèdre dispose d'un coin à angle droit (comme un coin d'un cube ), puis la place de la zone de la face opposée du coin à angle droit est la somme des carrés des zones de l'autre trois faces. Ce résultat peut être généralisé comme dans le «théorème de Pythagore n de dimension":
Laisserêtre des vecteurs orthogonaux dans ℝ n. Considérons le n simplex de dimension S avec des sommets
. (Pensez à la (n - 1) simplex de dimension avec des sommets
ne comprenant pas l'origine comme le "hypoténuse" de S et le reste (n - 1) de faces de dimension S que ses "jambes") Ensuite, le carré du volume de l'hypoténuse de S est la somme des carrés de la. les volumes des n branches.
Cette déclaration est illustré en trois dimensions par le tétraèdre dans la figure. Le "hypoténuse" est la base du tétraèdre à l'arrière de la figure, et les "jambes" sont les trois côtés émanant du sommet au premier plan. Comme la profondeur de la base augmente à partir du sommet, la surface des "jambes" augmente, tandis que celle de la base est fixée. Le théorème suggère que lorsque cette profondeur est à la création de valeur d'un sommet à droite, la généralisation du théorème de Pythagore applique. Dans une formulation différente:
Compte tenu d'unen-rectangularnsimplex de dimension, le carré de la (n- 1) -content de lafacette obstacle au droit sommet sera égal à la somme des carrés des (n- 1) -contents des facettes restantes.
Espaces de produits internes
Le théorème de Pythagore peut être généralisée à des espaces de produits internes, qui sont des généralisations des 2 dimensions et en 3 dimensions familières espaces euclidiens . Par exemple, une fonction peut être considérée comme un vecteur avec un nombre infini de composants dans un espace interne du produit, comme dans analyse fonctionnelle.
Dans un espace de produit intérieur, le concept de perpendicularité est remplacé par le concept de l'orthogonalité: deux vecteurs v et w sont orthogonaux si leur produit intérieur 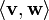 est zéro. Le produit scalaire est une généralisation du produit scalaire de vecteurs. Le produit scalaire est appelée la norme produit interne ou euclidienne produit interne. Cependant, d'autres produits scalaires sont possibles.
est zéro. Le produit scalaire est une généralisation du produit scalaire de vecteurs. Le produit scalaire est appelée la norme produit interne ou euclidienne produit interne. Cependant, d'autres produits scalaires sont possibles.
Le concept de longueur est remplacé par le concept de lanorme ||v|| d'un vecteurv, définie comme suit:
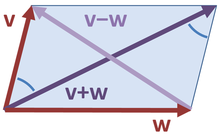
Dans un espace intérieur-produit, lethéorème de Pythagorestipule que pour toutes les deux vecteurs orthogonauxvetwnous avons
Voici les vecteurs v et w sont semblables aux côtés d'un triangle rectangle dont l'hypoténuse donnée par le vecteur somme v + w . Cette forme de théorème de Pythagore est une conséquence des propriétés du produit intérieur:
où les produits intérieurs des termes croisés sont nulles, en raison de l'orthogonalité.
Une autre généralisation du théorème de Pythagore dans un espace interne de produits à des vecteurs non orthogonaux est la règle du parallélogramme:
qui dit que le double de la somme des carrés des longueurs des côtés d'un parallélogramme est la somme des carrés des longueurs des diagonales. Toute norme qui satisfait cette égalité est ipso facto une norme correspondant à un produit scalaire.
L'identité de Pythagore peut être étendu à des sommes de plus de deux vecteurs orthogonaux. Si c 1 , v 2 , ..., v n sont des vecteurs orthogonaux deux à deux dans un espace intérieur-produit, puis application du théorème de Pythagore pour des paires successives de ces vecteurs (comme décrit pour 3 dimensions dans la section sur la géométrie des solides résultats dans) l'équation
L'identité de Parseval est une autre généralisation qui considère sommes infinies de vecteurs orthogonaux.
Pour le produit intérieur
(Best unhermitiennematrice définie positive etu *latransposée conjuguée deu) le théorème de Pythagore est:
oùPest uneprojection qui satisfait la relation:
La carte linéaire:
puis est uneprojection orthogonale.
La géométrie non-euclidienne
Le théorème de Pythagore est dérivé des axiomes dela géométrie euclidienne, et en fait, le théorème de Pythagore donnée ci-dessus ne tient pas dans un géométrie non-euclidienne.(Le théorème de Pythagore a été montré, en effet, pour êtreéquivalent à la parallèle d'Euclide (cinquième) Postulat.) En Autrement dit, dans la géométrie non-euclidienne, la relation entre les côtés d'un triangle doivent nécessairement prendre une forme non-pythagoricienne. Par exemple, dans géométrie sphérique, tous les trois côtés du triangle rectangle (disonsun,b, etc) délimitant un octant de la sphère unité avoir une longueur égale à π / 2, et tous ses angles sont droits, ce qui viole le théorème de Pythagore, carun 2+b 2≠c 2.
Voici deux cas de la géométrie non-euclidienne sont considered- géométrie sphérique et la géométrie plane hyperbolique; dans chaque cas, comme dans le cas euclidien pour les triangles non-droit, le résultat en remplaçant le théorème de Pythagore découle de la loi appropriée des cosinus.
Cependant, le théorème de Pythagore reste vrai dans la géométrie hyperbolique et la géométrie elliptique si la condition que le triangle soit droite est remplacé à la condition que deux des angles résumé à la troisième, dire A + B = C . Les côtés sont ensuite liées comme suit: la somme des surfaces des cercles de diamètres un et b est égale à la surface du cercle de diamètre c .
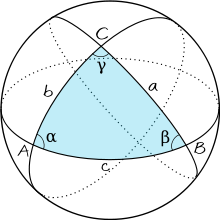
Géométrie sphérique
Pour tout triangle rectangle sur une sphère de rayonR(par exemple, si γ dans la figure est un angle droit), avec des côtésun,b,c, la relation entre les parties prend la forme:
Cette équation peut être calculée comme un cas particulier de laloi des cosinus sphérique qui applique à tous les triangles sphériques:
En utilisant la série de Maclaurin pour la fonction cosinus, cos x ≈ 1 - x 2 / 2 , on peut montrer que le rayon R tend vers l'infini et les arguments a / R, b / R c / R tend vers zéro, la sphérique relation entre les côtés d'un triangle rectangle se rapproche de la forme de théorème de Pythagore. En substituant l'quadratique approximative pour chacun des cosinus dans le rapport sphérique pour un triangle rectangle:
Multipliant les quantités entre parenthèses, le théorème de Pythagore est récupérée pour les grands rayonsR:
où lestermes d'ordre supérieurdeviennent négligeables queRdevient grand.
Géométrie hyperbolique
Pour un triangle en géométrie hyperbolique avec des côtésun,b,cet avec le côtécopposé à un angle droit, la relation entre les parties prend la forme:
cosh où est le cosinus hyperbolique. Cette formule est une forme particulière de la loi des cosinus hyperbolique qui applique à tous les triangles hyperboliques:
avec γ l'angle au sommet opposé du côtéc.
En utilisant lasérie de Maclaurinpour le cosinus hyperboliquecoshx≈ 1 +x 2/ 2, il peut être démontré que hyperbolique comme un triangle devient très faible (autrement dit, commeun,b, etctoute approche zéro), la relation hyperbolique pour un triangle rectangle se rapproche de la forme de théorème de Pythagore.
Géométrie différentielle
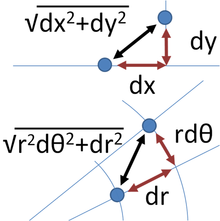
Sur un niveau infinitésimal, dans un espace tridimensionnel, le théorème de Pythagore décrit la distance entre deux points infiniment séparés que:
avec ds l'élément de distance et ( dx , dy , dz ), les composantes du vecteur séparant les deux points. Un tel espace est appelé un espace euclidien . Cependant, une généralisation de cette expression utile pour les coordonnées générales (pas seulement cartésienne) et des espaces généraux (pas seulement euclidienne) prend la forme:
où g ij est appelé le tenseur métrique. Il peut être une fonction de la position. Tel espaces courbes comprennent la géométrie de Riemann comme un exemple général. Cette formulation est également valable pour un espace euclidien de l'utilisation de coordonnées curvilignes. Par exemple, en coordonnées polaires :
Histoire
Il ya un débat si le théorème de Pythagore a découvert une fois ou plusieurs fois dans de nombreux endroits.
L'histoire du théorème peut être divisé en quatre parties: la connaissance destriplets pythagoriciens, la connaissance de la relation entre les côtés d'untriangle rectangle, la connaissance des relations entre les angles adjacents, et les preuves du théorème dans un système déductif.
Bartel Leendert van der Waerden (1903-1996) a conjecturé que triplets pythagoriciens ont été découverts algébriquement par les Babyloniens. Écrit entre 2000 et 1786 avant JC, l' Empire du Milieu égyptien papyrus Berlin 6619 comprend un problème dont la solution est le triplet pythagoricien 6: 8: 10, mais le problème ne mentionne pas un triangle. Le mésopotamienne tablette Plimpton 322 , écrit entre 1790 et 1750 avant JC sous le règne de Hammurabi le Grand, contient de nombreuses entrées étroitement liés à triplets pythagoriciens.
En Inde , l' Baudhayana Sulba Sutra , les dates sont données diversement comme entre le 8ème siècle avant JC et le 2e siècle avant JC, contient une liste de triplets de Pythagore a découvert algébrique, un énoncé du théorème de Pythagore, et un géométrique preuve de Pythagore théorème pour un isocèle triangle rectangle. Le Apastamba Sulba Sutra ( ca. 600 BC) contient une preuve numérique du théorème de Pythagore général, en utilisant un calcul de la zone. Van der Waerden croit qu '«il était certainement basé sur des traditions antérieures". Boyer (1991) pense que les éléments trouvés dans la Sulba-sũtram peuvent être de dérivation mésopotamienne.
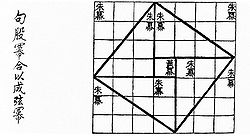
Avec contenu connus beaucoup plus tôt, mais dans des textes datant de survivants à peu près le premier siècle avant JC, le chinois texte Zhou Bi Suan Jing (周髀算经), ( L'arithmétique classique du gnomon et les trajectoires circulaires du Ciel ) donne un raisonnement le théorème de Pythagore pour la (3, 4, 5) de triangle en Chine, il est appelé le "théorème Gougu" (勾股定理). Pendant le dynastie des Han (202 avant JC à 220 après JC), triples de Pythagore apparaissent dans Les Neuf Chapitres sur la mathématique Art , avec une mention de triangles rectangles. Certains croient que le théorème surgi la première fois en Chine , où il est également connu comme le "Shang Gao Théorème" (商高定理), nommé d'après le duc de astronome et mathématicien de Zhou, dont le raisonnement a composé la plupart de ce qui était dans la Zhou Bi Suan Jing .
Pythagore , dont les dates sont couramment donné que 569 à 475 avant JC, a utilisé des méthodes algébriques pour construire triplets pythagoriciens, selon le commentaire de Proclus sur Euclid . Proclus, cependant, écrit entre 410 et 485 AD. Selon Sir Thomas L. Heath (1861-1940), aucune attribution spécifique du théorème de Pythagore existe dans la littérature grecque survivant des cinq siècles après Pythagore a vécu. Toutefois, lorsque des auteurs comme Plutarque et Cicéron attribués le théorème de Pythagore, ils l'ont fait d'une manière qui suggère que l'attribution a été largement connu et incontestable. "Que cette formule est à juste titre attribué à Pythagore personnellement, [...] on peut supposer qu'il appartient à la période très ancienne des mathématiques de Pythagore."
Autour de 400 avant JC, selon Proclus, Platon a donné une méthode pour trouver triplets pythagoriciens qui combine l'algèbre et la géométrie. Autour de 300 avant JC, dans d'Euclide les éléments , le plus ancien existant preuve axiomatique du théorème est présenté.
Dans la culture populaire
Le théorème de Pythagore a été soulevée dansla culture populairedans une variété de façons.
- Un verset de lachanson du major-général dans l'opéra-comique de Gilbert et Sullivan Les Pirates de Penzance, «À propos du binôme je fourmille avec beaucoup o 'nouvelles, avec de nombreux faits gaies sur le carré de l'hypoténuse", fait une oblique référence au théorème.
- Le Scarecrow dans le film Le Magicien d'Oz fait une référence plus spécifique au théorème. Dès réception de son diplôme de l' assistant, il présente immédiatement sa «connaissance» en récitant une version mutilée et incorrecte du théorème: "La somme des racines carrées de tous les deux côtés d'un triangle isocèle est égale à la racine carrée de la participation restante côté. Oh, joie! Oh, ravissement! Je ai un cerveau! "
- En 2000, l'Ouganda a publié une pièce de monnaie avec la forme d'un triangle isocèle. La queue de la pièce a une image de Pythagore et l'équation α 2 + β 2 = γ 2 , accompagné de la mention "Pythagore Millénaire".
 | |
- La Grèce,le Japon,Saint-Marin,Sierra Leoneetle Surinameont émis destimbres-postereprésentant Pythagore et le théorème de Pythagore.
- En Fiction spéculative de Neal Stephenson Anathem , le théorème de Pythagore est dénommé «le théorème Adrakhonic '. Une preuve géométrique du théorème est affiché sur le côté d'un navire étranger pour démontrer la compréhension par les étrangers des mathématiques.


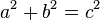
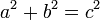
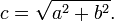
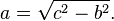
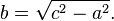
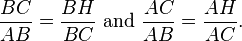
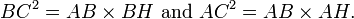
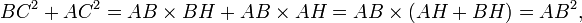
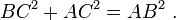
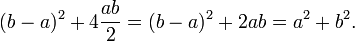
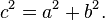
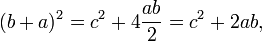
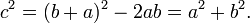
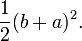
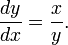
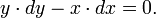
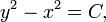
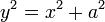
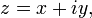
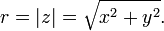
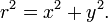
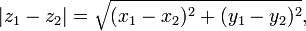
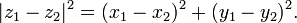
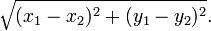
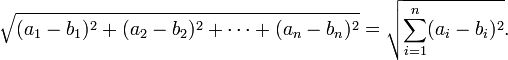
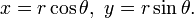
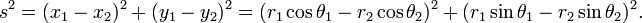
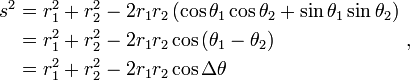
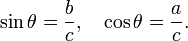
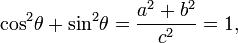
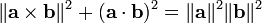
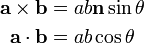
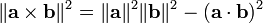
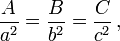
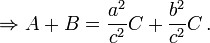
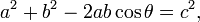
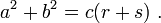
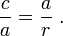
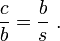
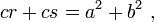

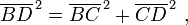
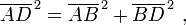
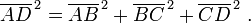
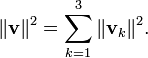
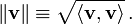
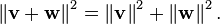
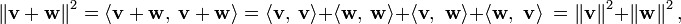
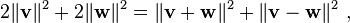
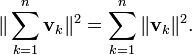
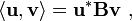
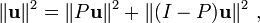
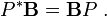
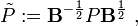
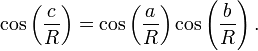
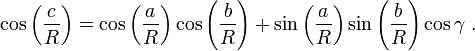
![1-\left(\frac{c}{R}\right)^2= \left[1-\left(\frac{a}{R}\right)^2 \right]\left[1-\left(\frac{b}{R}\right)^2 \right] + \ \mathrm{higher\ order\ terms}](../../images/1436/143667.png)