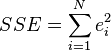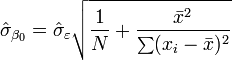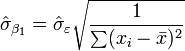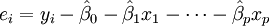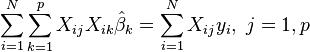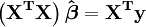L'analyse de régression

Saviez-vous ...

Cette sélection écoles a été choisi par SOS Enfants pour les écoles dans le monde en développement ne ont pas accès à Internet. Il est disponible en téléchargement intranet. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille près de la charité. Lire la suite ...

L'analyse de régression est une technique utilisée pour la modélisation et l'analyse de données numériques comprenant des valeurs d'une variable dépendante (variable de réponse) et d'un ou plusieurs variables indépendantes (variables explicatives). La variable dépendante dans l'équation de régression est modélisée comme une fonction des variables indépendantes, correspondant paramètres («constantes»), et un terme d'erreur. Le terme d'erreur est traité comme une variable aléatoire . Il représente la variation inexpliquée de la variable dépendante. Les paramètres sont estimés de façon à donner un "meilleur ajustement" des données. La plupart du temps le meilleur ajustement est évaluée en utilisant le moindres carrés méthode, mais d'autres critères ont également été utilisés.

La modélisation des données peut être utilisé sans qu'il y ait des connaissances sur les processus sous-jacents qui ont généré les données; dans ce cas, le modèle est un modèle empirique. En outre, dans la connaissance de la modélisation de la distribution de probabilité des erreurs ne est pas nécessaire. L'analyse de régression nécessite la formulation d'hypothèses concernant la distribution de probabilité des erreurs. Les tests statistiques sont effectués sur la base de ces hypothèses. En analyse de régression du terme «modèle» englobe à la fois la fonction utilisée pour modéliser les données et les hypothèses concernant les distributions de probabilité.

La régression peut être utilisé pour prédiction (y compris prévision des données de séries chronologiques), inférence, tests d'hypothèses, et la modélisation des relations causales. Ces utilisations de la régression se appuient fortement sur les hypothèses sous-jacentes étant satisfaits. L'analyse de régression a été critiquée comme étant mal utilisé à ces fins dans de nombreux cas où les hypothèses appropriées ne peuvent pas être vérifiées à tenir. Un facteur qui contribue à la mauvaise utilisation de la régression est qu'il peut prendre beaucoup plus de compétence pour critiquer un modèle que pour se adapter à un modèle.

Histoire de l'analyse de régression

La première forme de régression était la méthode des moindres carrés , qui a été publié par Legendre en 1805, et par Gauss en 1809. Le terme "moindres carrés" est du mandat de Legendre, moindres carrés. Cependant, Gauss a affirmé qu'il avait connu la méthode depuis 1795.

Legendre et Gauss fois appliqué la méthode au problème de déterminer, à partir d'observations astronomiques, les orbites des corps sur le soleil. Euler avaient travaillé sur le même problème (1748) sans succès. Gauss publié un autre développement de la théorie des moindres carrés en 1821, dont une version de la Théorème de Gauss-Markov.

Le terme «régression» a été inventé dans le XIXe siècle pour décrire un phénomène biologique, à savoir que la descendance d'individus exceptionnels ont tendance en moyenne à être moins exceptionnelle que leurs parents et plus comme leurs ancêtres plus éloignés. Francis Galton, cousin de Charles Darwin , a étudié ce phénomène et appliqué le terme un peu trompeuse " régression vers la médiocrité »à elle. Pour Galton, la régression ne avaient que cette signification biologique, mais son travail a ensuite été étendu par Udny Yule et Karl Pearson à un contexte statistique plus générale. Aujourd'hui, le terme «régression» est souvent synonyme de "moindres carrés ajustement de courbe ".

Hypothèses sous-jacentes

L'échantillon doit être représentatif de la population pour la prédiction d'inférence.
La variable dépendante est sujette à l'erreur. Cette erreur est supposé être une variable aléatoire , avec une moyenne de zéro. L'erreur systématique peut être présent, mais son traitement est hors de la portée de l'analyse de régression.
La variable indépendante est sans erreur. Si ce ne est pas le cas, la modélisation devrait être fait en utilisant Erreurs dans les variables de techniques de modèle.
Les prédicteurs doivent être linéairement indépendants, ce est à dire qu'il ne doit pas être possible d'exprimer toute prédicteur comme une combinaison linéaire des autres. Voir Multicollinear.
Les erreurs sont non corrélés, ce est le matrice de variance-covariance des erreurs est diagonale et chaque élément non nul est la variance de l'erreur.
La variance de l'erreur est constante ( homoscédasticité). Dans le cas contraire, les poids doivent être utilisés.
Les erreurs suivent une distribution normale . Sinon, le modèle linéaire généralisé doit être utilisé.

Régression linéaire

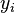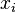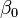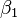Dans la régression linéaire, la spécification du modèle est que la variable dépendante, $y_i$ est un combinaison linéaire des paramètres (mais ne est pas nécessairement linéaire dans les variables indépendantes). Par exemple, dans la régression linéaire simple, il est une variable indépendante, $x_i$ , Et les deux paramètres, $\ Beta_0$ et $\ Beta_1$ :

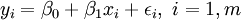
ligne droite: $y_i = \ beta_0 + \ beta_1 x_i + \ epsilon_i, \ i = 1, m \!$

Dans la régression linéaire multiple, il existe plusieurs variables indépendantes ou des fonctions de variables indépendantes. Par exemple, l'ajout d'un terme x _i ² à la régression précédente donne:

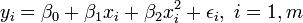
parabole: $y_i = \ beta_0 + \ beta_1 x_i + \ beta_2 x_i ^ 2 + \ epsilon_i, \ i = 1, m \!$

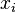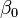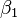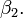
Ce est toujours la régression linéaire bien que l'expression sur le côté droit est quadratique de la variable indépendante $x_i$ Il est linéaire dans les paramètres $\ Beta_0$ , $\ Beta_1$ et $\ Beta_2.$

Dans les deux cas, 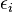$\ Epsilon_i$ est un terme d'erreur et l'indice 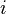$Je$ un index d'observation particulière. Compte tenu d'un échantillon aléatoire de la population, nous estimons les paramètres de la population et obtenons le modèle de régression linéaire échantillon: 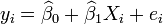$y_i = \ widehat {\ beta} _0 + \ widehat {\ beta} _1 X_i + E_I$ Le terme 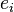$E_I$ est le résidu, 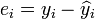$E_I = y_i - \ widehat {y} _i$ . Une méthode d'estimation est ordinaire [moindres carrés]. Ce procédé obtient des estimations de paramètres qui minimisent la somme du carré résidus, ESS:

$SSE = \ sum_ {i = 1} ^ {} N E_I ^ 2$

Minimisation de cette fonction se traduit par un ensemble de équations normales, un ensemble d'équations linéaires simultanées à des paramètres, qui sont résolus pour donner les estimateurs de paramètres, 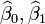$\ Widehat {\ beta} _0, \ widehat {\ beta} _1$ . Voir coefficients de régression pour les propriétés statistiques de ces estimateurs.

Illustration de la régression linéaire sur un ensemble de données (points rouges).

Dans le cas de la régression simple, les formules pour les estimations des moindres carrés sont

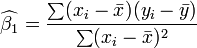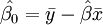
$\ Widehat {\ beta_1} = \ frac {\ sum (x_i- \ bar {x}) (y_i- \ bar {y})} {\ sum (x_i- \ bar {x}) ^ 2}$ et $\ Hat {\ beta_0} = \ bar {y} - \ hat {\ beta} \ bar {x}$

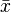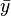où $\ Bar {x}$ est la moyenne (moyenne) de la $x$ valeurs et $\ Bar {y}$ est la moyenne de la 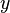$y$ des valeurs. Voir linéaires des moindres carrés (droite montage) pour une dérivation de ces formules et un exemple numérique. Dans l'hypothèse où le terme d'erreur de la population a une variance constante, l'estimation de variance qui est donnée par: 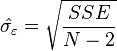$\ Hat {\ sigma _ {\ varepsilon}} = \ sqrt {\ frac {} {SSE N-2}}$ Ceci est appelé le erreur quadratique moyenne (RMSE) de la régression. Le erreurs standard des estimations des paramètres sont donnés par

$\ Hat \ sigma _ {\ beta_0} = \ hat \ sigma _ {\ varepsilon} \ sqrt {\ frac {1} {N} + \ frac {\ bar {x} ^ 2} {\ sum (x_i- \ bar x) ^ 2}}$

$\ Hat \ sigma _ {\ beta_1} = \ hat \ sigma _ {\ varepsilon} \ sqrt {\ frac {1} {\ sum (x_i- \ bar x) ^ 2}}$

Dans l'hypothèse en outre que le terme d'erreur de la population est normalement distribué, le chercheur peut utiliser ces erreurs-types estimées pour créer des intervalles de confiance et effectuer des tests d'hypothèses sur les paramètres de la population.

Modèle de données linéaire général

Dans le modèle plus général de régression multiple, y sont des variables indépendantes p: 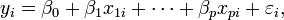$y_i = \ beta_0 + \ beta_1 x_ {} 1i + \ cdots + \ beta_p x_ {pi} + \ varepsilon_i,$ Les estimations des paramètres moindres carrés sont obtenues par p équations normales. Le résidu peut être écrite comme

$E_I = y_i - \ hat \ beta_0 - \ hat \ beta_1 x_1 - \ cdots - \ hat \ beta_p x_p$

Le équations normales sont

$\ Sum_ {i = 1} ^ {N} \ sum_ {k = 1} ^ {p} {ij} X_ X_ {ik} \ hat \ beta_k = \ sum_ {i = 1} ^ {} N X_ {ij} y_i, \ j = 1, p \,$

En notation matricielle, les équations normales sont écrites en tant que

$\ Mathbf {\ left (X ^ TX \ right) \ hat \ boldsymbol \ beta = X ^ Ty}$

Pour voir un exemple numérique régression linéaire (exemple)

Les diagnostics de régression

Une fois qu'un modèle de régression a été construit, il est important de confirmer la qualité de l'ajustement du modèle et de la signification statistique des paramètres estimés. Contrôles couramment utilisés de qualité de l'ajustement incluent le R-carré, les analyses du motif de résidus et tests d'hypothèses. La signification statistique est vérifiée par un F-test de l'ajustement global, suivie par des tests t de paramètres individuels.

Les interprétations de ces tests de diagnostic reposent lourdement sur les hypothèses du modèle. Bien que l'examen des résidus peut être utilisé pour invalider un modèle, les résultats d'un test t ou Test F sont de sens que si les hypothèses de modélisation sont satisfaits.

Le terme d'erreur ne peut pas avoir une distribution normale. Voir modèle linéaire généralisé.
La variable de réponse peut être discontinue. Pour binaire (zéro ou un) des variables, il ya la probit et modèle logit. Le modèle probit multivariée permet d'estimer conjointement la relation entre plusieurs variables dépendantes binaires et certaines variables indépendantes. Pour variables catégoriques ayant plus de deux valeurs, il ya la logit multinomial. Pour variables ordinales ayant plus de deux valeurs, il existe le logit ordonné et modèles de probit ordonné. Une alternative à ces procédures est la régression linéaire basée sur des corrélations polychoriques ou polyserial entre les variables catégorielles. Ces procédures diffèrent dans les hypothèses formulées au sujet de la distribution des variables dans la population. Si la variable est positive par de faibles valeurs et représente la répétition de la survenance d'un événement, compter des modèles comme la La régression de Poisson ou de la modèle binomial négatif peut être utilisé

Interpolation et extrapolation

Des modèles de régression prédire une valeur de la 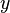$y$ les valeurs des variables données connues de la $x$ Variables. Si la prédiction doit être effectuée dans la plage de valeurs de la $x$ variables utilisées pour construire le modèle ce est connu comme l'interpolation . Prédiction dehors de la plage des données utilisées pour construire le modèle est connu comme extrapolation et il est plus risqué.

Régression non linéaire

Lorsque la fonction de modèle ne est pas linéaire dans les paramètres de la somme des carrés doit être minimisée par une procédure itérative. Cela introduit de nombreuses complications qui sont résumées dans les différences entre linéaire et non linéaire des moindres carrés

D'autres méthodes

Bien que les paramètres d'un modèle de régression sont habituellement estimés en utilisant la méthode des moindres carrés, d'autres procédés qui ont été utilisés sont les suivants:

Méthodes bayésiennes
Minimisation des écarts absolus, conduisant à régression quantile
Régression non paramétrique. Cette approche nécessite un grand nombre d'observations, que les données sont utilisées pour construire la structure du modèle ainsi que d'estimer les paramètres du modèle. Ils sont généralement de calcul intensif.

Logiciel

Tous les grands progiciels statistiques effectuent les types courants de l'analyse de régression correctement et d'une manière conviviale. La régression linéaire simple peut être fait en quelques tableurs. Il ya un certain nombre de programmes de logiciels qui effectuent des formes spécialisées de la régression, et les experts peuvent choisir d'écrire leur propre code pour l'aide langages de programmation ou de statistiques un logiciel d'analyse numérique.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Regression_analysis&oldid=198424867 "

We provide Linux to the World