Surface de Riemann

Riemann surface pour la fonction f (z) = sqrt (z)

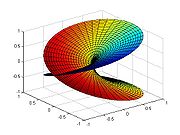
En mathématiques , en particulier dans analyse complexe, une surface de Riemann, d'abord étudié par et nommé d'après Bernhard Riemann , est un unidimensionnel variété complexe. Surfaces de Riemann peuvent être considérés comme des "versions" déformées du plan complexe : de proximité sur chaque point ils ressemblent à des taches du plan complexe, mais le global topologie peuvent être très différents. Par exemple, ils peuvent ressembler à une sphère ou d'un tore ou un couple de feuilles collées ensemble.

Le point principal de surfaces de Riemann est que fonctions holomorphes peuvent être définies entre eux. Surfaces de Riemann sont aujourd'hui considérés comme le cadre naturel pour l'étude du comportement global de ces fonctions, en particulier fonctions à valeurs multiples comme la racine carrée et autres fonctions algébriques, ou le logarithme .

Chaque surface de Riemann est une véritable analyse bidimensionnelle collecteur (soit un la surface), mais il contient plus de structure (en particulier un structure complexe) qui est nécessaire pour la définition des fonctions holomorphes sans ambiguïté. Un véritable variété bidimensionnelle peut être transformé en une surface de Riemann (généralement de plusieurs façons inéquivalentes) si et seulement si il est orientable. Donc, la sphère et tore admettent structures complexes, mais le Ruban de Möbius, la bouteille de Klein et plan projectif ne le font pas.

Faits géométriques sur des surfaces de Riemann sont les «gentils» que possible, et ils fournissent souvent l'intuition et la motivation des généralisations à d'autres courbes, collecteurs ou de variétés. Le Riemann-Roch est un excellent exemple de cette influence.

Définitions

Il existe plusieurs définitions équivalentes d'une surface de Riemann.

1. Une surface de Riemann X est un variété complexe de complexe une dimension. Cela signifie que X est un sage espace doté d'un soi-disant atlas: pour chaque point x ∈ X il ya une environnement, ce qui ressemble à l' plan complexe . La carte portant la structure du plan complexe de la surface de Riemann est appelé diagramme. Deux graphiques qui se chevauchent doivent être compatibles dans un certain sens.
2. Une surface de Riemann est un Variété riemannienne de (réel) dimension deux - où la surface de Riemann de nom avec un la structure conformationnelle. Encore une fois, le collecteur signifie que localement à tout point x de X, l'espace est censé être comme l'avion réel. Le supplément "Riemann» signifie que X est doté d'un soi-disant Riemannienne g métrique, ce qui permet de mesurer des angles sur le collecteur. Deux de ces mesures sont considérées équivalent si les angles qu'ils mesurent sont les mêmes. Le choix d'une métrique, et donc une classe d'équivalence de metrices X est sur le point de référence supplémentaire de la structure conformationnelle.

Une structure complexe donne lieu à une structure conforme à la norme en choisissant Métrique euclidienne donnée sur le plan complexe et à le transporter à X au moyen des cartes.

Exemples

La sphère de Riemann.

• Le plan complexe C est peut-être la surface la plus fondamentale de Riemann. La carte f (z) = z (la carte d'identité) définit un tableau C, et {f} est un atlas C. La carte g (z) = z ^* (le conjugué carte) définit également un tableau de la C et {g} est un atlas C. Les graphiques f et g ne sont pas compatibles, de sorte que cette dote C avec deux structures de surface différentes de Riemann. En fait, étant donné une surface de Riemann X et son atlas A, le conjugué atlas B = {f ^*: f ∈ A} ne est jamais compatible avec A, et lui confère X avec une structure distincte Riemann incompatibles.

• De façon analogue, chaque partie ouverte du plan complexe peut être considérée comme une surface de Riemann d'une manière naturelle. Plus généralement, toute partie ouverte d'une surface de Riemann est une surface de Riemann.

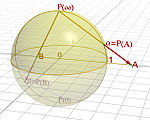
• Soit S = C ∪ {∞} et f (z) = z où z est compris dans S \ {∞} et g (z) = 1 / z, où z est compris dans S \ {0} et 1 / ∞ est défini à 0. graphiques sont ensuite f et g, ils sont compatibles, et {f, g} est un atlas S, S en faisant une surface de Riemann. Cette surface particulière est appelée Sphère de Riemann, car il peut être interprété comme enveloppant le plan complexe autour de la sphère. Contrairement au plan complexe, il est compact .

Un tore.

• La théorie des surfaces de Riemann compactes peut être démontré équivalent à celui de projective courbes algébriques qui sont définis sur les nombres complexes et non singulière. Par exemple, le tore C / (Z + Z τ), où τ est un nombre réel non-complexe, correspond, via la Fonction elliptique de Weierstrass associée au Z + τ treillis Z, à une courbe elliptique donnée par une équation

y ² = x ³ + ax + b.

Tori sont les seules surfaces de Riemann de une genre, les surfaces de genres g ultérieure sont assurés par le surfaces hyperelliptiques

y ² = P (x),

où P est un complexe polynôme de degré 2 g 1.

• Des exemples importants de surfaces de Riemann non-compacts sont fournis par prolongement analytique.

D'autres définitions et propriétés

Comme avec ne importe quelle carte entre les variétés complexes, une fonction f: M → N entre deux surfaces de Riemann M et N est appelé holomorphe si pour chaque tableau g dans le atlas de M et chaque tableau h dans l'atlas de N, la carte h o f o g ^-1 est holomorphe (en fonction de C à C) où elle est définie. La composition de deux cartes holomorphes est holomorphe. Les deux surfaces de Riemann M et N sont appelés biholomorphe (ou conformément équivalente à souligner le point de vue conforme) se il existe une fonction holomorphe bijective de M à N dont l'inverse est également holomorphe (il se avère que cette dernière condition est automatique et peut donc être omise). Deux surfaces de Riemann conformément équivalente sont à toutes fins pratiques identiques.

Orientabilité

Nous avons noté dans le préambule que tous les surfaces de Riemann, comme toutes les variétés complexes, sont orientable comme un véritable collecteur. La raison est que pour les graphiques complexes f et g avec fonction de transition h = f (g ^-1 (z)) nous pouvons considérer h comme une carte à partir d'un ensemble ouvert de R ² à R ² dont Jacobienne dans un point z est juste la carte réelle linéaire donnée par multiplication par le nombre complexe h '(z). Toutefois, le véritable facteur déterminant de la multiplication par un nombre complexe α égaux | α | ^2, de sorte que le jacobien de h possède déterminant positif. En conséquence, l'atlas complexe est un atlas orientés.

Fonctions

Chaque surface de Riemann non-compacte admet fonctions holomorphes non constantes (avec des valeurs en C). En fait, chaque surface de Riemann non-compacte est un Variété de Stein.

En revanche, sur une surface de Riemann compacte X chaque fonction holomorphe à valeur dans C est constante en raison de la principe du maximum. Cependant, il existe toujours non constante fonctions méromorphes (= des fonctions holomorphes avec les valeurs de la Sphère de Riemann C ∪ {∞}). Plus précisément, la domaine de la fonction X est une fini extension de C (t), le champ de fonction dans une variable, ce est à dire toutes les deux fonctions méromorphes sont algébriquement dépendants. Cette déclaration généralise à des dimensions supérieures, voir Siegel (1955).

Analytique vs algébrique

Le fait ci-dessus à propos de l'existence de fonctions méromorphes non constantes peut être utilisé pour montrer que ne importe quelle surface de Riemann compacte est un variété projective, ce est à dire peut être donnée par polynomiales équations intérieur d'un espace projectif. En fait, il peut être démontré que chaque surface de Riemann compacte peut être incorporé dans le plan projectif complexe. Ce est un théorème surprenant: les surfaces de Riemann sont donnés par des graphiques de rapiéçage localement. Si une condition globale, à savoir compacité, est ajouté, la surface est nécessairement algébrique. Cette caractéristique de surfaces de Riemann permet de les étudier avec soit les moyens de analytique ou géométrie algébrique. La déclaration correspondante pour les objets de dimension supérieure est faux, ce est à dire il ya deux complexes plis compacts qui ne sont pas algébrique. D'autre part, chaque variété complexe projective est nécessairement algébrique, voir Le théorème de Chow.

A titre d'exemple, considérons le tore T: = C / (Z + τ Z). La fonction de Weierstrass 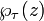appartenant au treillis Z + τ Z est un fonction méromorphe sur T. Cette fonction et son dérivé 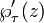générer le champ de T de fonction. Il se agit d'une équation

où les coefficients g et ₂ g ₃ dépendent de τ, donnant ainsi une courbe elliptique E _τ dans le sens de la géométrie algébrique. Inversion Ceci est accompli par la j-invariant j (E), qui peut être utilisé pour déterminer τ, et donc un tore.

Classification des surfaces de Riemann

Le royaume de surfaces de Riemann peut être divisé en trois régimes: les surfaces de Riemann hyperboliques, paraboliques et elliptiques. Cette distinction est donnée par la uniformisation théorème qui stipule que chaque Riemann surface simplement connexe est conformément équivalente une des opérations suivantes:

• le plan complexe C
• la sphère de Riemann C ∪ {∞}, également notée P ¹ C

ou

• la ouverte disque D: = {z ∈ C: | z | <1} ou équivalente, la demi-plan supérieur H: = {z ∈ C: Im (z)> 0}.

Selon l'équivalence des deux définitions données ci-dessus, le théorème de l'uniformisation peut également être formulée en termes de géométrie conforme: chaque surface de Riemann connecté X admet un unique, complète réelle deux dimensions Riemann métrique constante courbure -1, 0 ou une induction de la même structure conformationnelle. La surface X est appelé hyperbolique, parabolique et elliptique, respectivement. L'existence de ces trois types parallèle plusieurs (Non) Les euclidiennes.

La technique générale d'associer un collecteur X son une couverture universelle Y, et exprimant le X original comme quotient de Y par le groupe de transformations de pont donne un premier aperçu sur les surfaces de Riemann.

Elliptic surfaces de Riemann

Par définition, ce sont les surfaces X avec une courbure constante. Le Sphère de Riemann C ∪ {∞} est le seul exemple. ( courbes elliptiques sont des exemples de surfaces de Riemann paraboliques L'appellation vient de l'histoire:. courbes elliptiques sont associés à fonctions elliptiques, qui à leur tour se présentent pour calculer le circonférence du ellipses ).

Surfaces de Riemann paraboliques

Par définition, ce sont les surfaces X avec courbure constante 0. équivalente, par le théorème de l'uniformisation, la couverture universelle de X doit être le plan complexe.

Il ya donc trois possibilités pour X. Il peut être le même plan, un anneau ou un tore

T: = C / (Z ⊕ τ Z).

L'ensemble des représentants des classes à sont appelés domaines fondamentaux. Il faut prendre soin dans la mesure où deux tores sont toujours homeomorphic , mais en général pas biholomorphe à l'autre. Ce est la première apparition du problème de modules. Le module d'un tore peut être capturé par un numéro unique τ complexe avec partie imaginaire positive. En fait, l'espace de modules marquée ( Teichmüller espace) du tore est biholomorphe à demi-plan supérieur ou de manière équivalente le disque unité ouvert.

Hyperbolique surfaces de Riemann

Le Riemann surfaces à courbure -1 sont appelés hyperbolique. Ce groupe est le "plus grand" une.

Le célèbre Théorème de l'application conforme stipule que tout sous-ensemble strict simplement connexe du plan complexe est biholomorphe sur le disque de l'unité. Par conséquent, le disque ouvert avec le Poincaré-métrique de courbure constante -1 est le modèle local de toute surface de Riemann hyperbolique. Selon le théorème de l'uniformisation ci-dessus, toutes les surfaces sont hyperboliques quotients du disque unité.

Les exemples incluent toutes les surfaces avec genre g> 1 tels que les courbes hyper-elliptique.

Pour chaque surface de Riemann hyperbolique, le groupe fondamental est isomorphe à un Fuchsien groupe, et donc la surface peuvent être modélisées par un Fuchsien modèle H / Γ où H est la demi-plan supérieur et Γ est le groupe fuchsien. L'ensemble des représentants des classes à des H / Γ sont jeux libres et régulières et peuvent être façonnés en métrique polygones fondamentales. structures de Quotient que H / Γ sont généralisés à Variétés de Shimura.

Contrairement surfaces elliptiques et paraboliques, aucune classification des surfaces hyperboliques est possible. Toute ouverte sous-ensemble strict connecté du plan donne une surface hyperbolique; examiner le plan, moins une Ensemble de Cantor. Une classification est possible pour les surfaces de type fini: ceux qui groupe fondamental de type fini. Tout d'eux a un nombre fini de modules et ainsi un espace de dimension finie Teichmüller. Le problème de modules (résolu par Lars Ahlfors et prolongé par Lipman Bers) était de justifier l'allégation de Riemann que, pour une surface fermée de genre g, 3G - 3 paramètres complexes suffisent.

Quand une surface hyperbolique est compact, la superficie totale de la surface est 4π (g-1), où g est le genre de la surface; la zone est obtenue en appliquant le Formule de Gauss-Bonnet de la superficie du polygone de base.

Dans l'art et la littérature

• Un des Les œuvres de MC Escher, Imprimer Galerie, est posé sur une grille de plus en plus cyclique qui a été décrit comme une surface de Riemann.
• En Le roman de Aldous Huxley Brave New World, "Riemann Tennis de surface" est un jeu populaire.