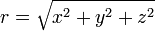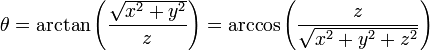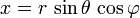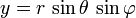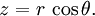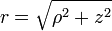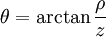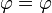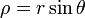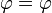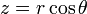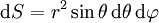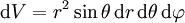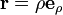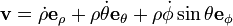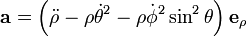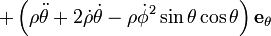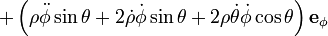Coordonnées sphériques

À propos de ce écoles sélection Wikipedia

SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .

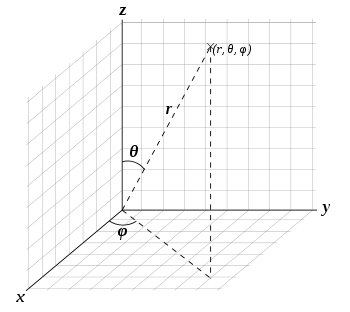
Un point tracée en utilisant le système de coordonnées sphérique

En mathématiques , le système de coordonnées sphérique est une système de coordonnées pour représenter des figures géométriques en trois dimensions à l'aide de trois coordonnées: la distance radiale d'un point fixe à partir d'une origine, le angle zénithal de l'axe z positif, et la angle d'azimut de l'axe des x positif.

Notation

Plusieurs conventions existent pour représenter les trois coordonnées. Conformément à l'Organisation internationale de normalisation ( ISO 31-11), en physique, ils sont généralement notée en (r, θ, φ) pour la distance radiale, zénith, et l'azimut, respectivement.

En mathématiques (américains), la notation pour zénith et l'azimut sont inversées comme φ est utilisé pour désigner l'angle zénithal θ et est utilisé pour désigner l'angle azimutal. Une autre complication est que certains textes de mathématiques liste l'azimut avant le zénith, mais cette convention est gaucher et devrait être évitée. La convention «mathématiques» a l'avantage d'être plus compatible dans le sens de θ avec la notation traditionnelle pour les deux dimensions du système de coordonnées polaires et les trois dimensions système de coordonnées cylindriques, tandis que la convention «physique» a une acceptation plus large géographiquement. Certains utilisateurs de la convention "physique" utilisent également φ pour les coordonnées polaires pour éviter le premier problème (comme ce est la norme ISO pour coordonnées cylindriques). Autres notation ρ utilise pour la distance radiale. La convention de notation de l'auteur de tout travail se rapportant à coordonnées sphériques doit toujours être vérifiée avant d'utiliser les formules et les équations de cet auteur. Cet article utilise la convention standard.

Définition

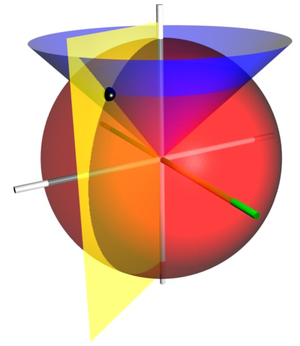
Le coordonner les surfaces des coordonnées sphériques (r, θ, φ). Le rouge sphère montre les points avec r = 2, le bleu cône présente les points avec θ = 45 °, et la demi-jaune plan montre les points avec φ = -60 °. L'axe z est vertical et l'axe des x est surligné en vert. Les trois surfaces se coupent au point P avec ces coordonnées (présentée comme une sphère noire); les coordonnées cartésiennes de P sont à peu près (0,707, -1,225, 1,414).

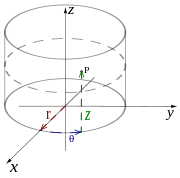
Les trois coordonnées (r, θ, φ) sont définies comme suit:

r ≥ 0 est la distance de l'origine à un point donné P.
0 ≤ θ ≤ π est l'angle entre l'axe z positif et la ligne formée entre l'origine et P.
0 ≤ φ <2π est l'angle entre l'axe des x positif et la ligne à partir de l'origine à la classe P projetée sur le plan xy.

φ est appelé l'azimut, tandis que θ est appelé le zénith ou angle de colatitude polaire.

θ et φ perdre de leur importance lorsque r = 0 et φ perd importance lorsque sin (θ) = 0 (à θ = 0 et θ = π).

Pour tracer un point à partir de ses coordonnées sphériques, aller unités r de l'origine le long de l'axe z positif, rotation θ autour de l'axe y dans la direction de l'axe x positif et tourner φ autour de l'axe z dans la direction de l'axe y positif.

Coordonner conversions de système

Comme le système de coordonnées sphérique ne est que l'un des nombreux systèmes de coordonnées tridimensionnelles, il existe des équations de conversion de coordonnées sphérique entre le système de coordonnées et d'autres.

Système de coordonnées cartésiennes

Les trois coordonnées sphériques sont obtenues à partir des coordonnées cartésiennes par:

$r = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$

${\ Theta} = \ arctan \ left (\ frac {\ sqrt {x ^ 2 + y ^ 2}} {z} \ right) = \ arccos \ gauche ({\ frac {z} {\ sqrt {x ^ 2 + y ^ 2 + z ^ 2}}} \ right)$

${\ Varphi} = \ arctan \ gauche ({\ frac {y} {x}} \ right).$

Notez que l'arctangente doit être définie de manière appropriée de façon à tenir compte du quadrant correct de 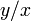$y / x$ . Le atan2 ou fonction équivalente accomplit ce à des fins de calcul.

Inversement, coordonnées cartésiennes peuvent être récupérés à partir des coordonnées sphériques par:

${X} = r \, \ sin \ theta \, \ cos \ varphi \ quad$

${Y} = r \, \ sin \ theta \, \ sin \ varphi \ quad$

${} Z = r \, \ cos \ theta. \ Quad$

Système de coordonnées géographiques

Le système de coordonnées géographiques est une version alternative du système de coordonnées sphérique, utilisé principalement dans la géographie mais aussi en mathématiques et en physique applications. En géographie, ρ est généralement abandonné ou remplacé par une valeur représentant l'altitude ou d'altitude.

Latitude 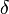${\ Delta} \,$ est le complément du zénith ou colatitude, et peut être converti par:

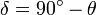${\ Delta} = 90 ^ \ circ - \ theta$ Ou

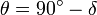${\ Theta} = 90 ^ \ circ - \ delta$ ,

si la latitude est généralement représenté par θ ainsi. Il se agit d'un angle de zénith provenant du plan xy avec un domaine de -90 ° ≤ θ ≤ 90 °. La longitude est mesurée en degrés à l'est ou à l'ouest de 0 °, de sorte que son domaine est -180 ° ≤ φ ≤ 180 °.

Coordonnées cylindriques

Le système de coordonnées cylindrique est une extrusion en trois dimensions du système de coordonnées polaires , avec une coordonnée z de décrire la hauteur d'un point au-dessus ou en dessous du plan xy. Le tuple complète de coordonnées est (r, φ, z).

Les coordonnées cylindriques peuvent être convertis en coordonnées sphériques par:

$r = \ sqrt {\ rho ^ 2 + z ^ 2}$

${\ Theta} = \ arctan \ frac {\ rho} {z}$

${\ Varphi} = \ varphi \ quad$

Les coordonnées sphériques peuvent être convertis en coordonnées cylindriques par:

$\ Rho = r \ sin \ theta \,$

$\ Varphi = \ varphi \,$

$z = r \ cos \ theta \,$

Applications

Le système de coordonnées géographiques applique les deux angles de la sphérique système d'exprimer endroits sur Terre coordonnées, les qualifiant de latitude et longitude. De même que la bidimensionnel système de coordonnées cartésiennes est utile dans l'avion, un système de coordonnées sphérique à deux dimensions est utile sur la surface d'une sphère. Dans ce système, la sphère est prise comme une sphère unitaire, de sorte que le rayon est généralement l'unité et peut être ignoré. Cette simplification peut également être très utile lorsqu'il se agit d'objets tels que matrices de rotation.

Les coordonnées sphériques sont utiles dans des systèmes qui sont symétriques par rapport à un point de l'analyse; une sphère qui a l'équation cartésienne x ² + y + z ^{2 2} = c ² a l'équation très simple r = c en coordonnées sphériques. Un exemple est dans la résolution d'un intégrale triple avec une sphère comme son domaine.

L'élément de surface d'une surface sphérique est

$\ DS mathrm = r ^ 2 \ sin \ theta \, \ mathrm d \ theta \, \ mathrm d \ varphi$

L'élément de volume est

$\ Mathrm dV = r ^ 2 \ sin \ theta \, \ mathrm dr \, \ mathrm d \ theta \, \ mathrm d \ varphi$

Coordonnées sphériques sont les coordonnées naturelles pour décrire et analyser des situations physiques où il ya une symétrie sphérique, comme le domaine de l'énergie potentielle entourant une sphère (ou point) avec la masse ou la charge. Deux importantes équations aux dérivées partielles , L'équation de Laplace et le Équation de Helmholtz, permettre à un séparation des variables en coordonnées sphériques. Les parties angulaires des solutions à ces équations prennent la forme de harmoniques sphériques.

Une autre application est la conception ergonomique, où r est la longueur du bras d'une personne à l'arrêt et les angles de décrire la direction du bras lorsqu'il atteint out.

Le concept de coordonnées sphériques peut être étendue à des espaces de dimensions supérieures et sont ensuite appelé hypersphériques coordonnées.

Cinématique

En coordonnées sphériques la position d'un point est écrit,

$\ Mathbf {r} = \ rho \ mathbf {e} _ \ rho$

sa vitesse est alors,

$\ Mathbf {v} = \ dot \ rho \ mathbf {e} _ \ rho + \ rho \ dot \ theta \ mathbf {e} _ \ theta + \ rho \ dot \ phi \ sin \ theta \ mathbf {e} _ \ phi$

et son accélération est,

$\ Mathbf {a} = \ left (\ ddot \ rho - \ rho \ dot \ theta ^ 2 - \ rho \ dot \ phi ^ 2 \ sin ^ 2 \ theta \ right) \ mathbf {e} _ \ rho$

$+ \ Left (\ rho \ ddot \ theta + 2 \ dot \ rho \ dot \ theta - \ rho \ dot \ phi ^ 2 \ sin \ theta \ cos \ theta \ right) \ mathbf {e} _ \ theta$

$+ \ Left (\ rho \ ddot \ phi \ sin \ theta + 2 \ dot \ rho \ dot \ phi \ sin \ theta + 2 \ rho \ dot \ theta \ dot \ phi \ cos \ theta \ right) \ mathbf { e} _ \ phi$

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Spherical_coordinate_system&oldid=197896135 "

We provide Linux to the World