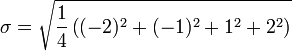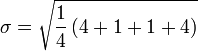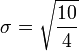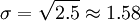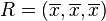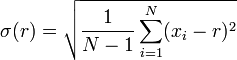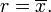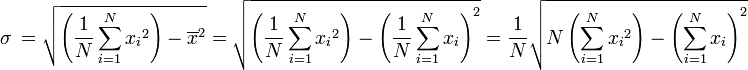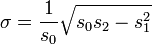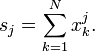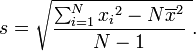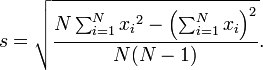L'écart-type
Contexte des écoles Wikipédia
Arrangeant une sélection Wikipedia pour les écoles dans le monde en développement sans internet était une initiative de SOS Enfants. Voir http://www.soschildren.org/sponsor-a-child pour connaître le parrainage d'enfants.
En probabilité et statistiques , l'écart-type d'une distribution de probabilité , variable aléatoire , ou la population ou multi-ensemble de valeurs est une mesure de la propagation de ses valeurs. L'écart-type est habituellement notée par la lettre σ (minuscules Sigma). Il est défini comme la racine carrée de la variance .
Pour comprendre l'écart type, garder à l'esprit que la variance est la moyenne des carrés des différences entre les points de données et la moyenne. La variance est sous forme de tableaux en unités carrés. L'écart-type, soit la racine carrée de cette quantité, mesure donc la propagation de données sur la moyenne, mesurée dans les mêmes unités que les données.
De façon plus formelle, l'écart-type est la moyenne quadratique (RMS) type des valeurs de leur moyenne arithmétique .
Par exemple, dans la population {4, 8}, la moyenne est 6 et les écarts par rapport aux moyennes sont {-2, 2}. Ces écarts carrés sont {4, 4} dont la moyenne (la variance) est 4. Par conséquent, l'écart type est égal à 2. Dans ce cas, 100% des valeurs dans la population sont à un écart-type de la moyenne.
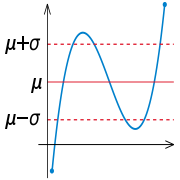
L'écart-type est la mesure la plus courante de dispersion statistique, la mesure de la façon dont les valeurs largement répandu dans un ensemble de données sont. Si nombreux points de données sont proches de la moyenne, alors l'écart type est faible; si nombreux points de données sont loin de la moyenne, alors l'écart type est grande. Si toutes les valeurs de données sont égales, l'écart type est égal à zéro.
Pour un population, l'écart type peut être estimé par un écart-type (s) de modification d'un échantillon. Les formules sont données ci-dessous.
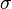 est une mesure de la dispersion des valeurs de la variable aléatoire loin de sa moyenne
est une mesure de la dispersion des valeurs de la variable aléatoire loin de sa moyenne 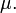
Définition et calcul
Un exemple simple
Supposons que nous souhaitions pour trouver l'écart type de l'ensemble des numéros 4 et 8.
Étape 1: trouver la moyenne arithmétique (ou moyenne) de 4 et 8,
Étape 2: trouver le type de chaque numéro de la moyenne,
Étape 3: carrés chacune des écarts (amplification des écarts plus importants et faire des valeurs négatives positif),
Étape 4: somme des carrés obtenus (comme une première étape à l'obtention d'une moyenne),
Etape 5: diviser la somme par le nombre de valeurs, qui ici est égal à 2 (soit une moyenne),
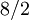 = 4.
= 4.
Étape 6: prendre la racine carrée positive du quotient (conversion d'unités au carré revenir à des unités régulières),
Ainsi, l'écart type est de 2.
L'écart-type d'une variable aléatoire
L'écart-type d'une variable aléatoire X est défini comme:
où E (X) est le valeur attendue de X, et Var (X) est la variance de x.
Toutes les variables aléatoires ne ont pas un écart-type, puisque ceux-ci valeurs attendues ne ont pas besoin existent. Par exemple, l'écart type d'une variable aléatoire qui suit une Distribution de Cauchy est indéfini parce que son E (X) ne est pas définie.
Si la variable aléatoire X prend les valeurs 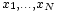 (Qui sont des nombres réels ) avec une probabilité égale, puis son écart-type peut être calculé comme suit. Tout d'abord, le moyen de X,
(Qui sont des nombres réels ) avec une probabilité égale, puis son écart-type peut être calculé comme suit. Tout d'abord, le moyen de X, 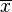 , Est défini comme un sommation:
, Est défini comme un sommation:
où N est le nombre d'échantillons prélevés. Ensuite, l'écart-type se simplifie
En d'autres termes, l'écart type d'une variable aléatoire uniforme discrète X peut être calculé comme suit:
- Pour chaque valeur
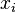 calculer la différence
calculer la différence 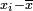 entre x i et la valeur moyenne
entre x i et la valeur moyenne  .
. - Calculer les carrés de ces différences.
- Trouver la moyenne des carrés des écarts. Cette quantité est la variance σ 2.
- Prendre la racine carrée de la variance.
L'expression ci-dessus peut également être remplacé par
L'égalité de ces deux expressions peut être démontré par un peu d'algèbre:
L'écart-type d'une variable aléatoire continue
Distributions continues donnent généralement une formule de calcul de l'écart-type en fonction des paramètres de la distribution. En général, l'écart type d'une variable aléatoire continue X avec fonction de densité de probabilité p (x) est
Où
Exemple
Nous allons montrer comment calculer l'écart-type d'une population. Notre exemple va utiliser les âges de quatre jeunes enfants: {5, 6, 8, 9}.
Étape 1. Calculer la moyenne arithmétique , 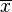 :
:
Nous avons N = 4 parce qu'il ya quatre points de données:
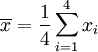 Suppléant N = 4
Suppléant N = 4
Étape 2. Calculer l'écart type, 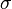 . (Depuis les quatre valeurs représentent l'ensemble de la population, nous ne utilisons pas la formule de l'écart type estimé dans ce cas):
. (Depuis les quatre valeurs représentent l'ensemble de la population, nous ne utilisons pas la formule de l'écart type estimé dans ce cas):
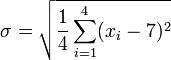 Remplaçant
Remplaçant 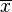 = 7 et N = 4
= 7 et N = 4
Donc, l'écart type des âges des quatre enfants est la racine carrée de 2,5, soit environ 1,58.
Se il en était fixé un échantillon tiré d'une population plus grande des enfants, et la question était à portée de main une estimation de l'écart type de la population, convention remplacerait le dénominateur N (ou 4) à l'étape 2 ici avec N -1 (ou 3 ).
Interprétation et application
Un grand écart-type indique que les points de données sont loin de la moyenne et un petit écart type indique qu'ils sont regroupés en étroite collaboration autour de la moyenne.
Par exemple, chacun des trois ensembles de données {0, 0, 14, 14}, {0, 6, 8, 14} et {6, 6, 8, 8} a une moyenne de 7. Les écarts-types sont 7, 5 et 1, respectivement. Le troisième set a un écart type beaucoup plus petit que les deux autres parce que ses valeurs sont toutes proche de 7. Dans un sens large, l'écart-type nous dit comment loin de la moyenne des points de données ont tendance à être. Il aura les mêmes unités que se rappelle les données. Si, par exemple, l'ensemble de données {0, 6, 8, 14} représente les âges de quatre frères et sœurs dans les années, l'écart type est de 5 ans.
Comme autre exemple, l'ensemble de données {1000, 1006, 1008, 1014} peut représenter les distances parcourues par quatre athlètes, mesurée en mètres. Elle a une moyenne de 1007 mètres, et un écart type de 5 mètres.
L'écart-type peut servir de mesure de l'incertitude. En sciences physiques, par exemple, l'écart type rapporté d'un groupe d'répétés mesures devrait donner le précision de ces mesures. Au moment de décider si les mesures sont d'accord avec une prédiction théorique, l'écart-type de ces mesures est d'une importance cruciale: si la moyenne des mesures est trop loin de la prédiction (avec la distance mesurée en écarts-types), alors la théorie testée probablement doit être révisée. Ce est logique car ils sortent la gamme des valeurs qui pourraient raisonnablement se attendre à se produire si la prédiction était correcte et l'écart type de quantifier de façon appropriée. Voir intervalle de prédiction.
Exemples de la vie réelle
La valeur pratique de la compréhension de l'écart-type d'un ensemble de valeurs est à apprécier le degré de variation il ya de la «moyenne» (signifie).
Temps
Comme un exemple simple, considérons les températures moyennes pour les villes. Alors que les deux villes peuvent avoir chacun une température moyenne de 60 ° F, il est utile de comprendre que la gamme pour les villes près de la côte est plus faible que pour les villes intérieures, qui précise que, alors que la moyenne est similaire, la chance de la variation est supérieur à l'intérieur des terres près de la côte.
Ainsi, une moyenne de 60 se produit pour une ville avec des sommets de 80 ° F et les bas de 40 ° F, et se produit également une autre ville avec des hauts et des bas de 65 de 55. L'écart-type nous permet de reconnaître que la moyenne de la ville avec la plus grande variation, et donc un écart-type supérieur, ne offrira pas une prédiction fiable de la température que la ville avec la plus petite variation et écart-type inférieur.
Sportif
Une autre façon de le voir est de considérer les équipes sportives. En tout ensemble de catégories, il y aura des équipes qui évaluent très à certaines choses et mal à d'autres. Il ya des chances, les équipes qui mènent au classement ne sera pas montrer telle disparité, mais seront assez bonne dans la plupart des catégories. Plus la déviation standard de leurs notes dans chaque catégorie, plus équilibrée et cohérente qu'ils pourraient être. Ainsi, une équipe qui est toujours mauvaise dans la plupart des catégories aura un faible écart type. Une équipe qui est toujours très bon dans la plupart des catégories aura également un écart type faible. Une équipe avec un écart-type élevé pourrait être le type d'équipe qui marque beaucoup (forte infraction), mais concède aussi beaucoup (de faible défense), ou vice versa, qui pourraient avoir une mauvaise infraction, mais compense en étant difficile de marquer sur -teams avec un écart-type supérieur sera plus imprévisible.
Essayer de prédire quelles équipes, sur ne importe quel jour donné, va gagner, peut comprendre en regardant les écarts-types des différents équipe "stats" votes, dans lequel les anomalies peuvent égaler forces contre les faiblesses de tenter de comprendre quels facteurs peuvent l'emporter que des indicateurs solides des résultats éventuels de notation.
En course, un pilote est chronométré sur tours successifs. Un conducteur ayant un faible écart type des temps au tour est plus cohérente que le conducteur avec un écart type supérieur. Cette information peut être utilisée pour aider à comprendre où les possibilités pourraient être trouvées pour réduire les temps au tour.
Financement
En finance, l'écart type est une représentation du risque associé à un titre donné (des actions, obligations, immobilier, etc.), ou le risque d'un portefeuille de valeurs mobilières. Le risque est un facteur important dans la détermination de la façon de gérer efficacement un portefeuille de placements, car il détermine la variation des rendements sur l'actif et / ou portefeuille et donne aux investisseurs une base mathématique pour les décisions d'investissement. Le concept global de risque, ce est que comme il augmente, le rendement attendu de l'actif va augmenter en raison de la prime de risque gagné - en d'autres termes, les investisseurs devraient se attendre à un rendement plus élevé sur un investissement lorsque ledit investissement comporte un niveau de risque plus élevé .
Par exemple, vous avez le choix entre deux stocks: Stock A renvoie historiquement 5% avec un écart type de 10%, tandis que l'action B retourne 6% et porte un écart-type de 20%. Sur la base de risque et de rendement, un investisseur peut décider que Stock A est le meilleur choix, parce supplémentaire point de pourcentage de Stock B de rendement généré (de 20% supplémentaires en termes de dollars) ne vaut pas le double du degré de risque associé à Stock A . Stock B est susceptible de tomber à court de l'investissement initial plus souvent Stock A dans les mêmes circonstances, et sera de retour seulement un point de pourcentage de plus en moyenne. Dans cet exemple, Stock A a le potentiel pour gagner 10% de plus que le rendement attendu, mais est également susceptible de gagner 10% de moins que le rendement attendu.
Calcul du rendement moyen (ou moyenne arithmétique) d'un titre sur un nombre donné de périodes va générer un rendement sur l'actif. Pour chaque période, en soustrayant le rendement attendu des résultats de rendement réel de la variance. Carré de la variance dans chaque période pour trouver l'effet du résultat sur le risque global de l'actif. Plus la variance dans une période, le plus grand risque à la sécurité porte. Prenant la moyenne des écarts au carré résulte dans la mesure de l'ensemble des unités de risque associés à l'actif. Trouver la racine carrée de cette variance se traduira par l'écart-type de l'outil d'investissement en question. Utilisez cette mesure, combinée avec le rendement moyen sur la sécurité, comme base pour comparer les valeurs mobilières.
Interprétation géométrique
Pour gagner quelques idées géométriques, nous allons commencer avec une population de trois valeurs, x 1, x 2, x 3. Ceci définit un point P = (x 1, x 2, x 3) dans R 3. Considérez la ligne L = {(r, r, r): r dans R}. Ce est la "diagonale principale" passant par l'origine. Si nos trois valeurs données étaient tous égaux, alors l'écart-type serait zéro et P serait mentir sur L. Il ne est donc pas déraisonnable de supposer que l'écart type est liée à la distance de P à L. Et ce est effectivement le cas. Déménagement orthogonale de P à la ligne L, on frappe le point:
dont les coordonnées sont la moyenne des valeurs Nous avons commencé avec. Un peu d'algèbre montre que la distance entre P et R (qui est la même que la distance entre P et la ligne L) est donnée par σ√ 3. Une formule analogue (avec 3 remplacé par N) est également valable pour une population de N valeurs; il faut alors travailler dans R N.
Règles pour les données normalement distribuées
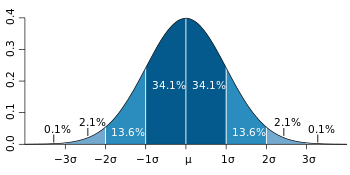
Dans la pratique, on suppose souvent que les données proviennent d'un peu près normalement distribuée population. Ce est souvent justifiée par le classique théorème central limite, qui dit que les sommes de plusieurs variables aléatoires indépendantes, identiquement distribuées tendent vers la distribution normale comme une limite. Si cette hypothèse est justifiée, environ 68% des valeurs sont à 1 écart type de la moyenne, environ 95% des valeurs sont dans les deux écarts-types et environ 99,7% se situent dans trois écarts-types. Ceci est connu comme la Règle 68-95-99.7, ou la règle empirique.
Le les intervalles de confiance sont les suivantes:
| σ | 68,26894921371% |
| 2σ | 95,44997361036% |
| 3σ | 99,73002039367% |
| 4σ | 99,99366575163% |
| 5σ | 99,99994266969% |
| 6σ | 99,99999980268% |
| 7σ | 99,99999999974% |
Pour les distributions normales, les deux points de la courbe qui sont un écart-type de la moyenne sont également la les points d'inflexion.
L'inégalité de Tchebychev
L'inégalité de Chebyshev prouve que dans ne importe quel ensemble de données, la quasi-totalité des valeurs sera plus proche de la valeur moyenne, où le sens de "près de" est spécifié par l'écart type. L'inégalité de Chebyshev implique que pour (presque) toutes les distributions aléatoires, et pas seulement celles normales, nous avons le plus faibles limites suivantes:
- Au moins 50% des valeurs sont à √2 écarts types de la moyenne.
- Au moins 75% des valeurs sont dans les deux écarts types de la moyenne.
- Au moins 89% des valeurs sont dans les 3 écarts-types de la moyenne.
- Au moins 94% des valeurs sont dans les 4 écarts types de la moyenne.
- Au moins 96% des valeurs sont à 5 écarts-types de la moyenne.
- Au moins 97% des valeurs sont dans les six écarts types de la moyenne.
- Au moins 98% des valeurs sont dans les 7 écarts types de la moyenne.
Et en général:
- Au moins (1 - 1 / k 2) × 100% des valeurs sont dans écarts-types de la moyenne de k.
Relation entre l'écart type et moyen
La moyenne et l'écart-type d'un ensemble de données sont généralement déclarés ensemble. Dans un certain sens, l'écart-type est une mesure «naturelle» de dispersion statistique si le centre de données est mesuré autour de la moyenne. Ce est parce que l'écart type de la moyenne est plus petite que de tout autre point. La déclaration précise est la suivante: supposons x 1, ..., x n sont des nombres réels et de définir la fonction:
Utilisation de calcul , ou simplement par complétant le carré, il est possible de montrer que σ (r) a un minimum unique au moyen:
(Ceci peut également être fait avec l'algèbre assez simple seul, puisque σ 2 (R) est assimilé à un polynôme du second degré).
Le coefficient de variation d'un échantillon est le rapport de l'écart type à la moyenne. C'est un nombre sans dimension qui peut être utilisé pour comparer la quantité de la variance entre les populations avec des moyens différents.
Méthodes de calcul rapides
Un peu plus rapidement (de manière significative pour l'exécution de l'écart type) moyen de calculer la norme de population déviation est donnée par la formule suivante (bien que des considérations doivent être prises pour erreur d'arrondi, dépassement arithmétique, et conditions Soupassement arithmétique):
ou
où S 2 sont définis les sommes de puissance S 0, S 1, par
De même pour l'écart type échantillon:
Ou de se exécuter sommes:

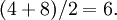
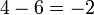
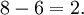
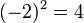
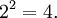
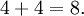
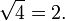
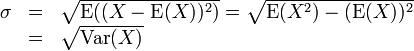
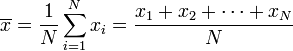
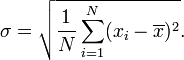
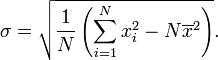
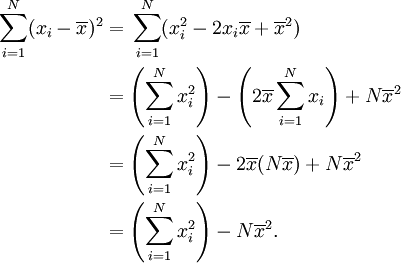
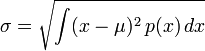
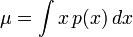
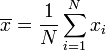

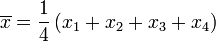
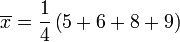
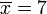
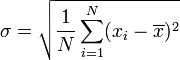
![\ Sigma = \ sqrt {\ frac {1} {4} \ left [(x_1 - 7) ^ 2 + (x_2 - 7) ^ 2 + (x_3 - 7) ^ 2 + (x_4 - 7) ^ 2 \ right ]}](../../images/135/13580.png)
![\ Sigma = \ sqrt {\ frac {1} {4} \ left [(5-7) ^ 2 + (6-7) ^ 2 + (8-7) ^ 2 + (9-7) ^ 2 \ right ]}](../../images/135/13581.png)