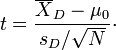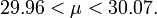Test de Student
Contexte des écoles Wikipédia
SOS Enfants, qui se déroule près de 200 sos écoles dans le monde en développement, a organisé cette sélection. Une bonne façon d'aider d'autres enfants est de parrainer un enfant
A t est tout -test test d'hypothèse statistique à laquelle la statistique de test a une la distribution t de Student si le hypothèse nulle est vraie. Il est appliqué lorsque taille de l'échantillon sont assez que l'utilisation de l'hypothèse d'une petite normalité et de l'associé test z conduit à incorrecte inférence.
Histoire
La statistique t a été introduit par William Gosset pour le suivi à peu de frais la qualité des bières de bière («étudiant» était son le nom de plume). Gosset était un statisticien pour le Guinness brasserie de Dublin, en Irlande , et a été embauché en raison de la politique d'innovation de Claude Guinness de recruter le meilleur diplômés de Oxford et Cambridge se appliquent à la biochimie et de statistiques aux procédés industriels de Guinness. Gosset publié le test t de Biometrika en 1908, mais a été forcé d'utiliser un nom de plume par son employeur qui considérait le fait qu'ils utilisent des statistiques comme un secret commercial. En fait, l'identité de Gosset était inconnu non seulement à ses collègues statisticiens, mais à son employeur - la société a insisté sur le pseudonyme afin qu'il puisse tourner un oeil aveugle à la violation de ses règles.
Aujourd'hui, il est plus généralement appliquée à la confiance qui peut être placé dans les décisions prises à partir de petits échantillons .
Utilisation
Un t-test est un test d'hypothèse statistique à laquelle la statistique de test a la distribution t de Student si l'hypothèse nulle est vraie. Il est appliqué lorsque les échantillons sont assez petit pour que l'aide d'une hypothèse de normalité et de la z-test associé mène à l'inférence incorrecte.
Parmi les tests de t les plus fréquemment utilisés sont:
- Un test de la hypothèse nulle que les moyens de deux normalement distribués populations sont égales. Étant donné deux ensembles de données, chacune caractérisée par sa moyenne , écart-type et le nombre de points de données, nous pouvons utiliser une sorte de test t de déterminer si les moyens sont distincts, à condition que les distributions sous-jacentes peuvent être considérés comme normaux. Tous ces tests sont généralement appelés tests t de Student, mais à proprement parler ce nom ne doit être utilisé si les écarts des deux populations sont également supposés être égaux; la forme du test utilisé lorsque cette hypothèse est tombé est parfois appelé Le test t de Welch. Il existe différentes versions du test t, selon que les deux échantillons sont
- indépendants les uns des autres (par exemple, les individus affectés au hasard en deux groupes), ou
- jumelé, de sorte que chaque membre d'un échantillon a une relation unique avec un membre particulier de l'autre échantillon (par exemple, les mêmes personnes mesurées avant et après une intervention scores, ou tests de QI d'un mari et la femme).
- Si la valeur calculée p-valeur est inférieure au seuil choisi pour signification statistique (habituellement le niveau de 0,05), l'hypothèse nulle qui indique généralement que les deux groupes ne diffèrent pas est rejetée en faveur d'une hypothèse alternative, qui stipule généralement que les groupes diffèrent.
- Un test pour savoir si la moyenne d'une population normalement distribuée a une valeur spécifiée dans une hypothèse nulle.
- Un test pour savoir si la pente d'une droite de régression diffère significativement de 0.
Une fois une valeur de t est déterminée, un p-valeur peut être trouvée en utilisant un tableau de valeurs de Loi de Student .
Hypothèses
- Distribution normale des données, testé en utilisant un test de normalité, comme Shapiro-Wilk et Test de Kolmogorov-Smirnov.
- Égalité des variances, testé en utilisant soit le F test, le plus robuste Le test de Levene, Le test de Bartlett, ou Brown-Forsythe essai.
- Les échantillons peuvent être indépendantes ou dépendantes, en fonction de l'hypothèse et le type d'échantillons:
- Échantillons indépendants sont habituellement des deux groupes choisis au hasard
- Échantillons dépendants sont soit des deux groupes appariés sur une variable (par exemple, l'âge) ou sont les mêmes personnes à l'essai deux fois (appelé mesures répétées)
Depuis tous les calculs sont faits sous réserve de l'hypothèse nulle, il peut être très difficile de trouver une hypothèse nulle raisonnable qui tient compte de l'égalité des moyens en présence de variances inégales. Dans le cas d'habitude, l'hypothèse nulle est que les différents traitements ne ont aucun effet - ce qui rend variances inégales intenable. Dans ce cas, il faut renoncer à la facilité d'utilisation de cette variante offerte par les progiciels statistiques. Voir également Problème Behrens-Fisher.
Type déterminer
Pour les novices, la question la plus difficile est souvent de savoir si les échantillons sont indépendants ou dépendants. Échantillons indépendants sont généralement constitués de deux groupes ayant aucune relation. Échantillons dépendants sont généralement constitués d'un échantillon apparié (ou un échantillon "paires") ou d'un groupe qui a été testé deux fois (mesures répétées).
Dépendantes t-tests sont également utilisés pour les échantillons appariés appariés, où deux groupes sont appariés sur une variable particulière. Par exemple, si nous avons examiné les hauteurs des hommes et des femmes dans une relation, les deux groupes sont appariés sur l'état de la relation. Cela exigerait un t -test dépendante parce que ce est un échantillon apparié (one man jumelé avec une femme). Autrement, nous pourrions recruter 100 hommes et 100 femmes, sans relation entre un homme et une femme particulière notamment; dans ce cas, nous devrions utiliser un test d'échantillons indépendants.
Un autre exemple d'un échantillon apparié serait de prendre deux groupes d'étudiants, correspondre à chaque étudiant dans un groupe avec un étudiant dans l'autre groupe basé sur un résultat de test de rendement, alors examiner combien chaque élève lit. Un exemple paire pourrait être deux étudiants qui obtiennent 90 et 91 ou deux étudiants qui ont obtenu 45 et 40 sur le même test. L'hypothèse serait que les élèves qui ont bien fait sur le test peuvent ou ne peuvent pas lire la suite. Autrement, nous pourrions recruter des étudiants ayant des notes faibles et les élèves avec des scores élevés dans les deux groupes et d'évaluer leurs montants de lecture indépendamment.
Un exemple de mesures répétées t -test serait si un groupe était pré- et post-test. (Cet exemple se produit dans l'éducation assez fréquemment.) Si un enseignant a voulu examiner l'effet d'une nouvelle série de manuels sur le rendement des élèves, (s) il pouvait tester la classe au début de l'année (pré-test) et à la fin de l'année (post-test). A t -test dépendante serait utilisé, le traitement de la pré-test et post-test en tant que variables appariées (appariés par l'étudiant).
Calculs
Dépendante t -test
Cette équation est utilisée lorsque les échantillons sont à charge; ce est quand il ya un seul échantillon qui a été testé deux fois (mesures répétées) ou quand il ya deux échantillons qui ont été appariés ou «paires».
Pour cette équation, les différences entre toutes les paires doivent être calculées. Les paires sont les scores prétest et posttest de soit une personne ou une personne dans un groupe adapté à une autre personne dans un autre groupe (voir tableau). La moyenne (X D) et l'écart type (s D) de ces différences sont utilisées dans l'équation. La constante 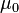 est non nul si vous voulez tester si la moyenne de la différence est sensiblement différente de celle
est non nul si vous voulez tester si la moyenne de la différence est sensiblement différente de celle 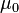 . Le degré de liberté utilisé est le N-1.
. Le degré de liberté utilisé est le N-1.
| Exemple de mesures répétées | |||
| Nombre | Nom | Test 1 | Test 2 |
|---|---|---|---|
| 1 | Micro | 35% | 67% |
| 2 | Melanie | 50% | 46% |
| 3 | Mélisse | 90% | 86% |
| 4 | Mitchell | 78% | 90% |
| Exemple de paires | |||
| Paire | Nom | Âge | Test |
|---|---|---|---|
| 1 | Jon | 35 | 250 |
| 1 | Jeanne | 36 | 340 |
| 2 | Pince-monseigneur | 22 | 460 |
| 2 | Jessy | 21 | 200 |
Exemple
Un échantillon aléatoire de vis ont des poids
- 30,02, 29,99, 30,11, 29,97, 30,01, 29,99
Calculer un intervalle de confiance de 95% pour le poids moyen de la population.
Supposons que la population est répartie comme N (μ, σ 2).
Poids moyen des échantillons de 30,015 est avec un écart type de 0,0497. Avec la moyenne et les cinq premiers poids, il est possible de calculer la sixième poids. Par conséquent, il existe cinq degrés de liberté.
Nous pouvons trouver en regardant dans la table que pour un intervalle de confiance de 95% et cinq degrés de liberté, la valeur est 2,571. 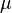 .
.
c.-à-
Si nous avons goûté plusieurs fois, notre intervalle serait capturer le véritable poids moyen de 95% du temps; Ainsi, nous sommes sûrs à 95% que le véritable poids moyen de toutes les vis se situera entre 29,96 et 30,07
Alternatives à l'épreuve de t
Rappelons que le test t peut être utilisé pour tester l'égalité des moyennes de deux populations normales avec inconnue, mais égale, la variance.
- Pour détendre l'hypothèse de normalité, un alternative non-paramétrique pour le test t peut être utilisé, et les choix habituels sont:
- pour des échantillons indépendants, le Test de Mann-Whitney
- pour les échantillons connexes, soit la test binomial ou Test des rangs signés de Wilcoxon
- Pour tester l'égalité des moyennes de plus de deux populations normales, un Analyse de la variance peut être effectuée
- Pour tester l'égalité des moyennes de deux populations normales avec variance connue, un Z-test peut être effectué
Implémentations
Plus tableurs et des programmes de statistiques comprennent les implémentations de test t de Student.
Calculatrices en ligne
- Jumelés / non apparié / Welch T-Test Calculator GraphPad