Sous-ensemble

Euler diagramme démontrant
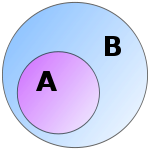
A est un sous-ensemble de B

Diagramme de Venn montrant
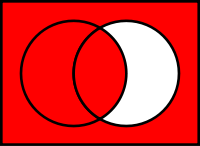
A est un sous-ensemble de B. Le cercle de gauche est A, les bonnes pièces B. rouges indiquent les situations possibles. La situation dans laquelle quelque chose est à l'intérieur du cercle A, mais pas dans B ne est pas rouge, donc impossible.

En mathématiques , en particulier dans la théorie des ensembles , un ensemble A est un sous-ensemble d'un ensemble B si A est "contenue" à l'intérieur B. Notez que A et B peut coïncider. La relation d'un ensemble étant un sous-ensemble d'un autre est appelé l'inclusion ou de confinement.

Définitions

Si A et B sont des ensembles et tous les élément de A est aussi un élément de B, alors:

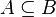• A est un sous-ensemble de (ou est inclus dans) B, notée ,

ou de façon équivalente

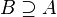• B est un sur-ensemble de (ou inclus) A, noté .

Si A est un sous-ensemble B, mais A ne est pas égale à B (ie il existe au moins un élément de B ne figure pas dans A), puis

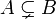• A est aussi un sous-ensemble (ou strict) de B; ce est écrit comme .

ou de façon équivalente

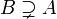• B est un sur-ensemble approprié de A; ce est écrit comme .

Pour tout ensemble S, la relation d'inclusion ⊆ est un ordre partiel sur l'ensemble 2 ^S de tous les sous-ensembles de S (la jeu de puissance de S).

Les symboles et ⊃ ⊂

D'autres auteurs préfèrent utiliser les symboles et ⊃ ⊂ pour indiquer sous-ensemble et sur-ensemble, respectivement, à la place de 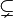et 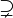. Cette utilisation permet ⊆ ⊂ et analogue et à ≤ <Par exemple, si x ≤ y alors x peut être égal à y, ou peut-être pas, mais si x <y, x ne est pas égal à y certainement, mais est strictement inférieur à y . De même, en utilisant le "⊂ signifie sous-ensemble" convention, si A ⊆ B, puis A peut être ou ne pas être égal à B, mais si A ⊂ B, alors A est certainement pas égal à B.

Exemples

• L'ensemble {1, 2} est un sous-ensemble de {1, 2, 3}.
• Tout ensemble est un sous-ensemble de lui-même, mais pas un sous-ensemble.
• Le ensemble vide, ∅ écrite, est également un sous-ensemble d'un ensemble donné X. (Cette déclaration est vacuously vrai, voir la preuve ci-dessous) L'ensemble vide est toujours un sous-ensemble, à l'exception de lui-même.
• L'ensemble {x: x est un nombre premier supérieur à 2000} est un sous-ensemble de {x: x est un nombre impair supérieur à 1 000}
• L'ensemble des nombres naturels est un sous-ensemble approprié de l'ensemble des nombres rationnels et l'ensemble de points dans un segment de ligne est un sous-ensemble de l'ensemble de points dans une ligne . Ce sont des exemples de contre-intuitive dans lequel à la fois la partie et le tout sont infinis, et la partie a le même nombre d'éléments que l'ensemble (voir Cardinalité des ensembles infinis).

Propriétés

Proposition 1

Le ensemble vide est un sous-ensemble de chaque ensemble.

Preuve: Compte tenu de tout ensemble A, nous souhaitons prouver que ø est un sous-ensemble de A. Il se agit de montrer que tous les éléments de ø sont des éléments de A. Mais il n'y a aucun élément de ø.

Pour le mathématicien expérimenté, l'inférence "ø n'a pas d'éléments, de sorte que tous les éléments de ø sont des éléments d'un« est immédiate, mais il peut être plus pénible pour le débutant. Depuis ø n'a pas de membres du tout, comment "ils" être membres d'autre chose? Il peut aider à penser l'inverse. Afin de prouver que ø ne était pas une partie de A, nous devons trouver un élément de ø qui ne était pas aussi un élément de A. Comme il n'y a pas d'éléments de ø, cela est impossible et donc ø est en effet une partie de A.

Proposition 2

La proposition suivante dit que l'inclusion est une ordre partiel.

Si A, B et C sont des ensembles puis la cale suivant:

réflexivité: A ⊆ A

antisymétrie: A ⊆ B et B ⊆ A si et seulement si A = B

transitivité: Si A ⊆ B et B ⊆ C alors A ⊆ C

Proposition 3

La proposition suivante dit que pour tout ensemble S le jeu de puissance de S ordonné par inclusion est une bornées réseau, et donc de concert avec les distributive et de compléter les lois pour les syndicats et les intersections (voir Les lois fondamentales de l'algèbre ensemble), montrent que ce est un Algèbre de Boole.

Si A, B et C sont des parties d'un ensemble S puis la cale suivante:

existence d'un moins élément et un plus grand élément:

• ø ⊆ A ⊆ S (ce ø ⊆ A est la proposition 1 ci-dessus.)

existence de rejoint:

• A ⊆ A ∪ B
• Si A ⊆ C et B ⊆ C alors A ∪ B ⊆ C

existence de répond:

• A ∩ B ⊆ A
• Si C ⊆ A et C ⊆ B puis C ⊆ A ∩ B

Proposition 4

La proposition suivante dit que, la déclaration "A ⊆ B", est équivalent à diverses autres déclarations impliquant les syndicats, les intersections et complète.

Pour tout deux ensembles A et B, l'suivantes sont équivalentes:

• A ⊆ B
• A ∩ B = A
• A ∪ B = B
• A - B = ø
• B '⊆ A'

Cela montre que la relation de jeu inclusion peut être caractérisée par l'une des opérations de réglage de l'union ou l'intersection, ce qui signifie que la notion d'ensemble inclusion est axiomatique superflue étant donné l'une de ces opérations et de l'égalité.

Proposition 5

Si le nombre d'éléments de l'ensemble A est n, le nombre de tous les sous-ensembles de A est égale à .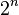

La preuve, ce est un exercice de l'induction.

Autres propriétés de l'inclusion

L'inclusion est canonique ordre partiel dans le sens que chaque ensemble partiellement ordonné (X, 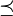) Est isomorphe à une certaine collection d'ensembles ordonnés par inclusion. Les nombres ordinaux sont un exemple simple, si chaque ordinal n est identifié avec l'ensemble [n] de tous les ordinaux inférieurs ou égaux à n, puis un ≤ b si et seulement si [a] ⊆ [b].

Pour le puissance réglée 2 ^S d'un ensemble S, l'ordre partiel d'inclusion est (jusqu'à une Afin isomorphisme) la Produit cartésien de k = | S | (la cardinalité de S) des copies de l'ordre partiel sur {0,1} pour lesquels 0 <1. Ceci peut être illustré par l'énumération S = {s _{1, S 2,} ..., s _k} et associer à chaque sous-ensemble T ⊆ S ( ce est-à-dire avec chaque élément de 2 ^S) Z-uplets de la k {0,1} ^k dont la i ième coordonnée est 1 si et seulement si s _i est un élément de T.