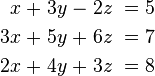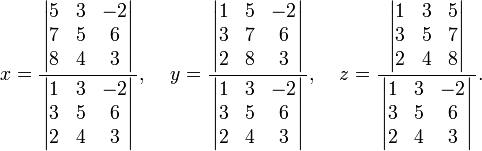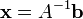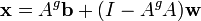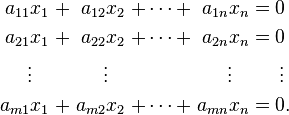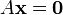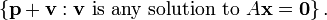Système d'équations linéaires
Contexte des écoles Wikipédia
SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Les enfants SOS est le plus grand don de charité du monde enfants orphelins et abandonnés la chance de la vie familiale.
En mathématiques , un système d'équations linéaires (ou système linéaire) est une collection de équations linéaires impliquant le même ensemble de Variables. Par exemple,
est un système de trois équations à trois variables x, y, z. Une solution à un système linéaire est une affectation de numéros à des variables telle que toutes les équations sont satisfaites simultanément. Un solution au système ci-dessus est donnée par
car elle rend tous les trois équations valide.
En mathématiques, la théorie des systèmes linéaires est la base et un élément fondamental de l'algèbre linéaire , un sujet qui est utilisé dans la plupart des régions des mathématiques modernes. Computational algorithmes pour trouver les solutions sont une partie importante de algèbre linéaire numérique, et jouent un rôle de premier plan dans l'ingénierie , la physique , la chimie , l'informatique et l'économie . Un système d'équations non linéaires est souvent approchée par un système linéaire (voir linéarisation), une technique utile lors d'un modèle mathématique ou simulation par ordinateur d'un système relativement complexe.
Très souvent, les coefficients des équations sont réels ou des nombres complexes et les solutions sont recherchées dans la même série de numéros, mais la théorie et les algorithmes se appliquent pour les coefficients et les solutions dans toute domaine. Pour les solutions dans un domaine intégrante comme le anneau des entiers , ou dans d'autres structures algébriques , d'autres théories ont été développées. Voir, par exemple, programmation linéaire pour les solutions entières, base de Gröbner pour polynômes coefficients et inconnues, ou encore la géométrie tropicale pour l'algèbre linéaire dans une structure plus exotique.
Exemple élémentaire
Le type le plus simple du système linéaire implique deux équations et deux variables:
Un procédé pour la résolution d'un tel système est le suivant. Tout d'abord, résoudre l'équation absolue pour  sur le plan de
sur le plan de 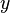 :
:
Maintenant remplacer cette expression pour x dans l'équation de fond:
Cela se traduit par une seule équation impliquant uniquement la variable 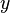 . Résolution donne
. Résolution donne 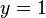 , Et son remplacement par ce retour dans l'équation pour
, Et son remplacement par ce retour dans l'équation pour  rendements
rendements 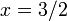 . Cette méthode se généralise à des systèmes avec des variables supplémentaires (voir «d'élimination des variables" ci-dessous, ou de l'article sur l'algèbre élémentaire .)
. Cette méthode se généralise à des systèmes avec des variables supplémentaires (voir «d'élimination des variables" ci-dessous, ou de l'article sur l'algèbre élémentaire .)
Forme générale
Un système général d'équations m linéaires à n inconnues peut être écrit comme
Ici 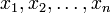 sont les inconnues,
sont les inconnues, 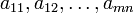 sont les coefficients du système, et
sont les coefficients du système, et 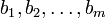 sont les termes constants.
sont les termes constants.
Souvent, les coefficients et les inconnues sont réels ou des nombres complexes , mais entiers et des nombres rationnels sont également considérés, comme les polynômes et les éléments d'un résumé structure algébrique .
Equation vectorielle
Un point de vue très utile est que chaque inconnu est un poids pour un vecteur colonne dans un combinaison linéaire.
Cela permet à tous la langue et de la théorie des espaces vectoriels (ou plus généralement, modules) pour être mises à profit. Par exemple, la collecte de toutes les combinaisons linéaires possibles des vecteurs sur le côté gauche est appelé leur durée, et les équations ont une solution juste au moment où le vecteur de droite est dans cette période. Si chaque vecteur à l'intérieur de cette séquence a exactement une expression en tant que combinaison linéaire des vecteurs de gauche données, toute solution est unique. En tout état de cause, la durée a une base de vecteurs linéairement indépendants qui ne garantissent exactement une expression; et le nombre de vecteurs dans cette base (sa dimension) ne peut pas être plus grand que m ou n, mais il peut être plus petite. Ce est important parce que si on a M vecteurs indépendants une solution est garantie quel que soit le côté droit, et par ailleurs non garantie.
équation matricielle
L'équation vectorielle est équivalente à une matrice équation de la forme
où A est une matrice m × n, x est un vecteur colonne à n entrées, et b est un vecteur colonne à m entrées.
Le nombre de vecteurs dans une base pour la durée est exprimée en maintenant la rang de la matrice.
jeu de Solution
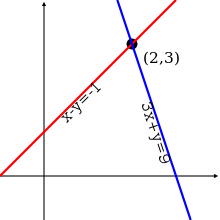
Une solution d'un système linéaire est une attribution de valeurs aux variables x 1, x 2, ..., x n de telle sorte que chacune des équations est satisfaite. L' ensemble de toutes les solutions possibles est appelé solution définie.
Un système linéaire peut comporter l'une quelconque des trois manières possibles:
- Le système a une infinité de solutions.
- Le système a une seule solution unique.
- Le système n'a pas de solution.
Interprétation géométrique
Pour un système impliquant deux variables (x et y), chaque équation linéaire détermine une ligne sur le xy - plan . Parce que la solution d'un système linéaire doit satisfaire à toutes les équations, la solution prévue est l' intersection de ces lignes, et est donc soit une ligne, un seul point, ou ensemble vide.
Pour trois variables, chaque équation linéaire détermine un plan de espace à trois dimensions, et l'ensemble de la solution est l'intersection de ces plans. Ainsi l'ensemble de la solution peut être un plan, une ligne, un seul point, ou l'ensemble vide.
Pour n variables, chaque équation linéaire détermine un hyperplan n l'espace de dimension. L'ensemble de la solution est l'intersection de ces hyperplans, qui peut être un plat de toute dimension.
Comportement général

En général, le comportement d'un système linéaire est déterminée par la relation entre le nombre d'équations et le nombre d'inconnues:
- Habituellement, un système avec moins d'équations que d'inconnues a une infinité de solutions ou des solutions rares parfois uniques ( détection comprimé). Un tel système est également connu comme un système sous-déterminé.
- Habituellement, un système ayant le même nombre d'équations et inconnues a une seule solution unique.
- Habituellement, un système avec plus d'équations que d'inconnues n'a pas de solution. Un tel système est également connu comme un système surdéterminé.
Dans le premier cas, la dimension de l'ensemble de la solution est généralement égal à n - m, où n est le nombre de variables et m est le nombre d'équations.
Les images suivantes illustrent cette trichotomie dans le cas de deux variables:

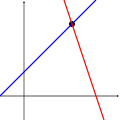
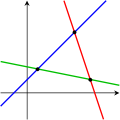
Une équation Deux équations Trois équations
Le premier système a une infinité de solutions, à savoir tous les points sur la ligne bleue. Le deuxième système présente une seule solution unique, à savoir l'intersection des deux lignes. Le troisième système n'a pas de solution, puisque les trois lignes part aucun point commun.
Gardez à l'esprit que les images ci-dessus montrent que le cas le plus commun. Il est possible pour un système de deux équations à deux inconnues ne pas avoir de solution (si les deux lignes sont parallèles), ou pour un système de trois équations à deux inconnues pour être solvable (si les trois lignes se croisent en un seul point). En général, un système d'équations linéaires peut se comporter différemment que prévu si les équations sont linéairement dépendante, ou si deux ou plusieurs des équations sont incompatibles .
Propriétés
Indépendance
Les équations du système linéaire sont indépendants si aucun des équations peut être dérivé algébriquement des autres. Lorsque les équations sont indépendantes, chaque équation contient de nouvelles informations sur les variables, et en supprimant l'une des équations augmente la taille de l'ensemble de la solution. Pour équations linéaires, l'indépendance logique est le même que indépendance linéaire.
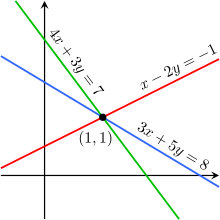
Par exemple, les équations
ne sont pas indépendants - ils sont la même équation lorsque l'échelle par un facteur de deux, et ils seraient produire des graphiques identiques. Ceci est un exemple d'équivalence dans un système d'équations linéaires.
Pour un exemple plus compliqué, les équations
ne sont pas indépendants, car la troisième équation est la somme des deux autres. En effet, l'une quelconque de ces équations peuvent être dérivées à partir des deux autres, et l'une quelconque des équations peut être retiré sans affecter l'ensemble de la solution. Les graphiques de ces équations sont trois lignes qui se croisent en un seul point.
Cohérence

Un système linéaire est conforme si elle a une solution, et incompatible contraire. Lorsque le système est incohérent, il est possible de dériver un contradiction à partir des équations, qui peuvent toujours être réécrits comme la déclaration 0 = 1.
Par exemple, les équations
sont incompatibles. En effet, en soustrayant la première équation à partir de la seconde et en multipliant les deux côtés du résultat par 1/6, on obtient 0 = 1. Les graphiques de ces équations sur la Plane xy sont une paire de des lignes parallèles.
Il est possible pour les trois équations linéaires sont incompatibles, même si deux d'entre elles sont compatibles ensemble. Par exemple, les équations
sont incompatibles. En ajoutant les deux premières équations ensemble donne 3 x 2 + y = 2, qui peut être soustraite de la troisième équation pour obtenir 0 = 1. Notez que deux de ces équations ont une solution commune. Le même phénomène peut se produire pour un certain nombre d'équations.
En général, les incohérences se produisent si les côtés gauche des équations dans un système sont linéairement dépendants, et les termes constants ne répondent pas à la relation de dépendance. Un système d'équations dont les côtés gauche sont linéairement indépendants est toujours cohérente.
En d'autres mots, selon la Rouché-Capelli théorème, tout système d'équations (surdéterminé ou autre) est incompatible si le rang de la matrice augmentée est plus grande que le rang de la matrice de coefficients. Si, d'autre part, les rangs de ces deux matrices sont égales, le système doit avoir au moins une solution. La solution est unique si et seulement si le rang est égal au nombre de variables. Sinon, la solution générale a k paramètres libres où k est la différence entre le nombre de variables et le rang; par conséquent, dans un tel cas, il existe une infinité de solutions.
Équivalence
Deux systèmes linéaires utilisant le même ensemble de variables sont équivalentes si chacune des équations du second système peut être dérivée à partir des équations algébriques dans le premier système, et vice-versa. Deux systèmes sont équivalentes si l'une ou les deux sont incompatibles chaque équation de l'un d'eux est une combinaison linéaire des équations de l'autre. Il se ensuit que deux systèmes linéaires sont équivalentes si et seulement si ils ont le même ensemble de solutions.
Résolution d'un système linéaire
Il existe plusieurs algorithmes pour résoudre un système d'équations linéaires.
Décrivant la solution
Lorsque l'ensemble de la solution est fini, il est réduit à un seul élément. Dans ce cas, l'unique solution est décrite par une séquence d'équations dont la main gauche côtés sont les noms des inconnues et les côtés de la main droite sont les valeurs correspondantes, par exemple 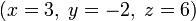 . Quand une commande sur les inconnues a été fixé, par exemple, le ordre alphabétique la solution peut être décrit comme un vecteur de valeurs, comme
. Quand une commande sur les inconnues a été fixé, par exemple, le ordre alphabétique la solution peut être décrit comme un vecteur de valeurs, comme 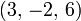 pour l'exemple précédent.
pour l'exemple précédent.
Il peut être difficile de décrire un ensemble avec une infinité de solutions. En règle générale, certaines des variables sont désignés comme libre (ou indépendant, ou en tant que paramètres), ce qui signifie qu'ils peuvent prendre ne importe quelle valeur, tandis que les variables restantes sont fonction des valeurs des variables libres.
Par exemple, considérons le système suivant:
La solution mis à ce système peut être décrit par les équations suivantes:
Ici z est la variable libre, tandis que x et y dépendent de z. Ne importe quel point dans le jeu de solution peut être obtenue en choisissant une première valeur de z, puis en calculant les valeurs correspondantes de x et y.
Chaque variable libre donne l'une de l'espace de solution degré de liberté, dont le nombre est égal à la dimension de l'ensemble de la solution. Par exemple, la solution prévue pour l'équation ci-dessus est une ligne, depuis un point dans l'ensemble de la solution peut être choisi en spécifiant la valeur du paramètre z. Une solution infinie d'ordre supérieur peut décrire un avion, ou un ensemble de plus grande dimension.
Des choix différents pour les variables libres peuvent conduire à des descriptions d'un même ensemble de la solution. Par exemple, la solution aux équations ci-dessus peut en variante être décrit comme suit:
Ici, la variable x est libre, et y et z sont dépendants.
Élimination des variables
La méthode la plus simple pour résoudre un système d'équations linéaires est d'éliminer des variables à plusieurs reprises. Cette méthode peut être décrite comme suit:
- Dans la première équation, pour résoudre l'une des variables en fonction des autres.
- Branchez cette expression dans les équations restantes. Cela donne un système d'équations avec un de moins équation et un de moins inconnue.
- Continuez jusqu'à ce que vous avez réduit le système à une seule équation linéaire.
- Résolvez cette équation, puis sauvegarder substitut jusqu'à ce que toute solution soit trouvée.
Par exemple, considérons le système suivant:
Résolution de la première équation donne pour x = x 2 + z 5 - 3 y, et de brancher ce dans les deuxième et troisième rendements équation
. Résolution de la première de ces équations pour les rendements y y = 2 + 3 z, et de brancher ce dans les secondes rendements équation z = 2 Nous avons maintenant:
En substituant z = 2 dans la deuxième équation donne y = 8, et son remplacement par z = 2 et y = 8 dans les premiers rendements de l'équation x = -15. Par conséquent, l'ensemble de la solution est le point (x, y, z) = unique (-15, 8, 2).
la réduction de la rangée
En matière de réduction de ligne, le système linéaire est présentée comme une matrice augmentée:
Cette matrice est ensuite modifié à l'aide opérations élémentaires sur les lignes jusqu'à ce qu'il atteigne forme réduite de Gauss. Il ya trois types d'opérations élémentaires sur les lignes:
- Type 1: échanger les positions de deux rangées.
- Type 2: Multipliez une rangée par un non nulle scalaire.
- Type 3: Ajouter à une ligne un multiple scalaire d'un autre.
Étant donné que ces opérations sont réversibles, la matrice augmentée produite représente toujours un système linéaire qui est équivalente à l'original.
Il ya plusieurs algorithmes spécifiques pour réduire une rangée matrice augmentée, dont la plus simple est l'élimination de Gauss et Élimination de Gauss-Jordan. Le calcul suivant montre l'élimination de Gauss-Jordan appliquée à la matrice ci-dessus:
La dernière matrice est sous forme réduite de Gauss, et représente le système x = -15, y = 8, z = 2. Une comparaison avec l'exemple dans la section précédente sur l'élimination algébrique des variables montre que ces deux méthodes sont en fait le même; la différence réside dans la façon dont les calculs sont écrites.
La règle de Cramer
La règle de Cramer est une formule explicite pour la solution d'un système d'équations linéaires, à chaque variable donnée par un quotient de deux déterminants . Par exemple, la solution du système
est donnée par
Pour chaque variable, le dénominateur est le déterminant de la matrice de coefficients, alors que le numérateur est le déterminant d'une matrice dans laquelle une colonne a été remplacé par le vecteur de termes constants.
Bien que la règle de Cramer est important en théorie, il a peu de valeur pratique pour les grandes matrices, depuis le calcul des grands déterminants est un peu lourd. (En effet, les grands déterminants sont le plus facilement calculé en utilisant la réduction de la ligne.) En outre, la règle de Cramer possède des propriétés numériques très pauvres, le rendant impropre à résoudre même les petits systèmes de façon fiable, à moins que les opérations sont effectuées en arithmétique rationnelle avec une précision infinie.
solution de matrice
Si le système d'équation est exprimée sous la forme d'une matrice 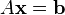 , L'ensemble de la solution peut également être exprimé sous forme de matrice. Si la matrice A est carrée (a m lignes et n = m colonnes) et a rang plein (toutes les lignes de m sont indépendants), le système a une solution unique donnée par
, L'ensemble de la solution peut également être exprimé sous forme de matrice. Si la matrice A est carrée (a m lignes et n = m colonnes) et a rang plein (toutes les lignes de m sont indépendants), le système a une solution unique donnée par
où 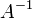 est le inverse de A. Plus généralement, indépendamment du fait que m = n ou non, et quel que soit le rang de A, toutes les solutions (se il en existe) sont donnés en utilisant le Pseudo-inverse de A, notée
est le inverse de A. Plus généralement, indépendamment du fait que m = n ou non, et quel que soit le rang de A, toutes les solutions (se il en existe) sont donnés en utilisant le Pseudo-inverse de A, notée 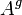 , Comme suit:
, Comme suit:
où 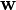 est un vecteur de paramètres libres qui se étend sur toute possible n × 1 vecteurs. Une condition nécessaire et suffisante pour que ne importe quelle solution (s) d'exister, ce est que la solution obtenue à l'aide potentielle
est un vecteur de paramètres libres qui se étend sur toute possible n × 1 vecteurs. Une condition nécessaire et suffisante pour que ne importe quelle solution (s) d'exister, ce est que la solution obtenue à l'aide potentielle 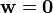 satisfaire
satisfaire 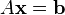 - À savoir que
- À savoir que 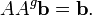 Si cette condition ne est pas vérifiée, le système d'équations est incohérente et n'a pas de solution. Si la condition est vérifiée, le système est conforme et au moins une solution existe. Par exemple, dans le cas mentionné ci-dessus dans laquelle A est carrée et de plein rang,
Si cette condition ne est pas vérifiée, le système d'équations est incohérente et n'a pas de solution. Si la condition est vérifiée, le système est conforme et au moins une solution existe. Par exemple, dans le cas mentionné ci-dessus dans laquelle A est carrée et de plein rang, 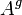 égale tout simplement
égale tout simplement 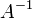 et l'équation de la solution générale se simplifie en
et l'équation de la solution générale se simplifie en 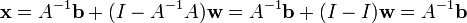 comme indiqué précédemment, où
comme indiqué précédemment, où 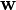 a complètement abandonné la solution, ne laissant qu'une seule solution. Dans d'autres cas, cependant,
a complètement abandonné la solution, ne laissant qu'une seule solution. Dans d'autres cas, cependant, 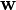 reste et donc une infinité de valeurs potentielles du vecteur de paramètre libre
reste et donc une infinité de valeurs potentielles du vecteur de paramètre libre 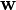 donner une infinité de solutions de l'équation.
donner une infinité de solutions de l'équation.
D'autres méthodes
Alors que les systèmes de trois ou quatre équations peuvent être facilement résolus par la main, les ordinateurs sont souvent utilisés pour des systèmes plus grands. L'algorithme standard pour résoudre un système d'équations linéaires est basée sur l'élimination de Gauss avec quelques modifications. Tout d'abord, il est essentiel pour éviter la division par un petit nombre, qui peuvent conduire à des résultats erronés. Cela peut être fait en réordonnant les équations si nécessaire, un processus connu sous le nom pivotement. Deuxièmement, l'algorithme ne fait pas exactement élimination de Gauss, mais il calcule la LU décomposition de la matrice A. Ce est surtout un outil d'organisation, mais il est beaucoup plus rapide si l'on doit résoudre plusieurs systèmes avec la même matrice A, mais différents vecteurs b.
Si la matrice A a une structure spéciale, ce qui peut être exploitée pour obtenir des algorithmes plus rapides ou plus précises. Par exemple, les systèmes équipés d'un symétrique matrice définie positive peut être résolu deux fois plus vite avec le Décomposition de Cholesky. Récurrence de Levinson est une méthode rapide pour Matrices de Toeplitz. Méthodes spéciales existent également pour les matrices avec de nombreux éléments zéro (soi-disant matrices creuses), qui apparaissent souvent dans les applications.
Une approche totalement différente est souvent prise pour de très grands systèmes, qui, autrement, prendre trop de temps ou de la mémoire. L'idée est de commencer avec une première approximation de la solution (qui ne doit pas être exacts à tous), et de changer cette approximation en plusieurs étapes pour se rapprocher de la vraie solution. Une fois que l'approximation est suffisamment précise, ce est considéré comme étant la solution au système. Cela conduit à la classe de méthodes itératives.
Systèmes homogènes
Un système d'équations linéaires est homogène si toutes les conditions sont constantes zéro:
Un système homogène est équivalente à une équation de la forme de la matrice
où A est une matrice m × n, x est un vecteur colonne à n entrées, et 0 est le vecteur nul avec des entrées de m.
jeu de Solution
Chaque système homogène présente au moins une solution, dite solution zéro (ou solution triviale), qui est obtenu en affectant la valeur de zéro pour chacune des variables. Si le système possède une matrice non singulière (det (A) ≠ 0), alors il est aussi la seule solution. Si le système possède un matrice singulière alors il ya un ensemble de solutions avec un nombre infini de solutions. Cet ensemble de solutions a les propriétés supplémentaires suivantes:
- Si u et v sont deux vecteurs représentant des solutions à un système homogène, alors la somme de vecteur u + v est également une solution au système.
- Si u est un vecteur représentant une solution à un système homogène, et R est tout scalaire, alors R u est aussi une solution au système.
Ce sont exactement les propriétés requises pour la solution établi pour être la sous-espace linéaire de R n. En particulier, la solution réglé à un système homogène est le même que le espace nul de la matrice A correspondant.
Rapport aux systèmes non homogènes
Il existe une relation étroite entre les solutions d'un système linéaire et les solutions du système homogène correspondant:
Plus précisément, si p est une solution particulière au système linéaire Ax = b, alors l'ensemble de la solution peut être décrit comme
Géométriquement, cela dit que l'ensemble de la solution A x = b est un traduction de l'ensemble de la solution A x = 0. Plus précisément, le plat pour le premier système peut être obtenu par la traduction de la sous-espace linéaire pour le système homogène par le vecteur p.
Ce raisonnement ne se applique que si le système A x = b a au moins une solution. Cela se produit si et seulement si le vecteur b se situe dans la image de la Une transformation linéaire.


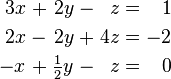
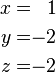
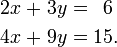
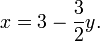
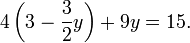
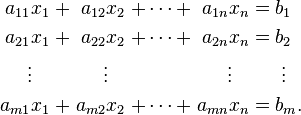
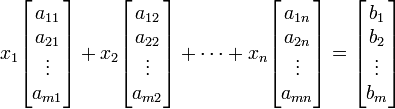
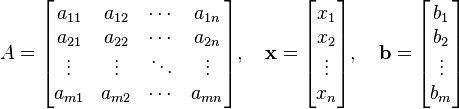
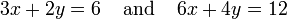
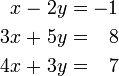

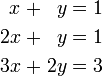
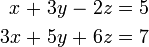
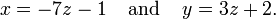
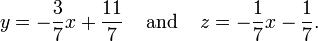
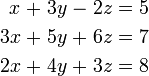
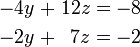
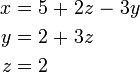
![\ Left [\ begin {array} {rrr | r} 1 & 3 & -2 et 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {array} \ right] \ text { .}](../../images/1643/164330.png)
![\ Begin {align} \ left [\ begin {array} {rrr | r} 1 & 3 & -2 et 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {array} \ droite] et \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et 0 \\ & -4 et 12 -8 \\ & 2 & 4 & 3 & 8 \ end {array } \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et 0 \\ & -4 et 12 -8 et \\ 0 et -2 et 7 & -2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et \\ 0 & 1 & 2 -3 et 0 \\ & -2 et 7 et - 2 \ end {array} \ right] \\ & \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et \\ 0 & 1 & 2 -3 et \\ 0 & 0 & 1 & 2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 0 & 0 9 \\ & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 0 & 0 et -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array} \ right]. \ end {align}](../../images/1643/164331.png)