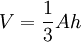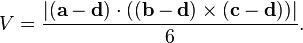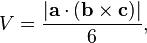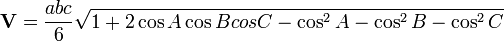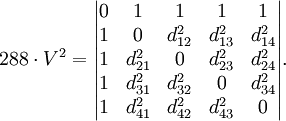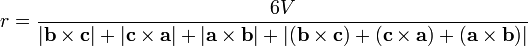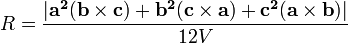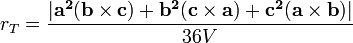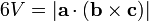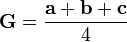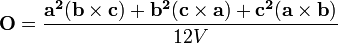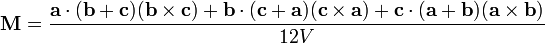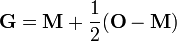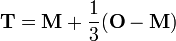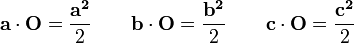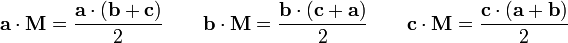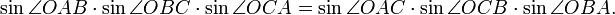Tétraèdre

Saviez-vous ...

SOS Enfants, un organisme de bienfaisance de l'éducation , a organisé cette sélection. Parrainage d'enfants aide les enfants du monde en développement à apprendre aussi.

Tétraèdre régulier
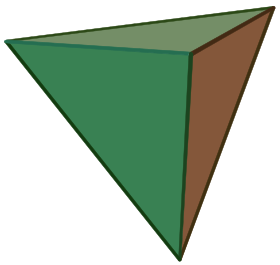(Cliquez ici pour le modèle de rotation)
Type	Solide de Platon
Éléments	F = 4, E = 6 V = 4 (χ = 2)
Faces de côtés	4 {3}
Symbole Schläfli	{3,3} et {s} 2,2
Symbole de Wythoff	3 \| 2 3 \| 2 2 2
Coxeter-Dynkin
Symétrie	T _d, A _3, [3,3], (332 *)
groupe de rotation	T [3,3] ^+, (332)
Références	U _01, C _15, W ₁
Propriétés	Régulier convexe deltaèdre
Dièdre	70.528779 ° = arccos (1/3)
3.3.3 ( Vertex figure)	Auto-double ( polyèdre dual)
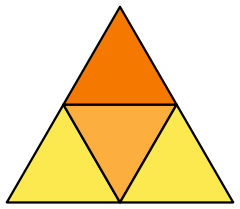Net

Un tétraèdre (pluriel: tétraèdres) est un polyèdre composé de quatre triangulaires visages, dont trois qui répondent à chaque vertex. Un tétraèdre régulier est celui dans lequel les quatre triangles sont réguliers, ou "équilatéral" et est l'un des solides de Platon .

Le tétraèdre est une sorte de pyramide , le deuxième type le plus commun; une pyramide a une base plate, et au-dessus des faces triangulaires, mais la base peut être de toute forme polygonale, et pas seulement carrée ou triangulaire.

Comme tous polyèdres convexes, un tétraèdre peut être plié à partir d'une seule feuille de papier.

Formules pour tétraèdre régulier

Pour un tétraèdre régulier de la longueur du bord 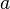$une$ :

Surface	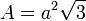$A = a ^ 2 \ sqrt {3} \,$
Volume	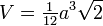$V = \ begin {matrix} {1 \ over12} \ end {matrix} a ^ 3 \ sqrt {2} \,$
Hauteur	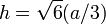$h = \ sqrt {6} (a / 3) \,$
Angle entre un bord et un visage	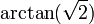$\ Arctan (\ sqrt {2}) \,$ (Env. 55 °)
Angle entre deux faces	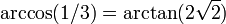$\ Arccos (1/3) = \ arctan (2 \ sqrt {2}) \,$ (Env. 71 °)
Angle entre les segments joignant le centre et les sommets	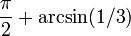${\ Pi \ over 2} + \ arcsin (1/3) \,$ (Env. 109,471 °)
Angle solide à un sommet sous-tendu par une face	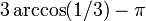$3 \ arccos (1/3) - \ pi \,$ (Env. 0,55129 stéradians)
Rayon de circonscrite	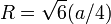$R = \ sqrt {6} (A / 4) \,$
Rayon de insphere qui est tangente aux faces	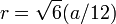$r = \ sqrt {6} (a / 12) \,$
Rayon de midsphere qui est tangente à bords	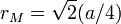$R_m = \ sqrt {2} (A / 4) \,$
Rayon de exspheres	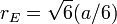$r_E = \ sqrt {6} (A / 6) \,$
Distance à exsphere centre d'un sommet	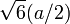$\ Sqrt {6} (a / 2) \,$

On notera que par rapport au plan de base de la la pente d'un visage ( 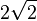$2 \ sqrt {2}$ ) Est le double de celui d'un bord ( $\ Sqrt {2}$ ), Ce qui correspond au fait que la distance horizontale recouverte de la base de la apex long d'un bord est deux fois plus que le long de la médiane d'un visage. En d'autres termes, si C est la centre de gravité de la base, la distance de C à un sommet de la base est le double de celle de C au point milieu d'un bord de la base. Cela découle du fait que les médianes d'un triangle se coupent en son centre de gravité, et ce point divise chacun d'eux en deux segments, dont l'un est deux fois plus longue que l'autre (voir la preuve).

Volume de ne importe quel tétraèdre

Le volume de ne importe quel tétraèdre est donnée par la formule du volume de la pyramide:

$V = \ frac {1} {3} Ah \,$

où A est la surface de la base et la hauteur h de la base vers le sommet. Ce est le cas pour chacun des quatre choix de la base, de sorte que les distances entre les sommets aux faces opposées sont inversement proportionnels aux surfaces de ces faces.

Pour un tétraèdre dont les sommets sont a = (a _1, a _2, a _3), b = (b _1, b _2, b _3), c = (c _1, c _2, c _3), et d = (d ₁ , d _2, d _3), le volume est de (1/6) · | det (A - B, B - C, C - D) |, ou toute autre combinaison de paires de sommets qui forment un tout simplement branchés graphique. Ce peut être réécrite en utilisant un point produit et un produit en croix , ce qui donne

$V = \ frac {| (\ mathbf {a} - \ mathbf {d}) \ cdot ((\ mathbf {b} - \ mathbf {d}) \ times (\ mathbf {c} - \ mathbf {d}) ) |} {6}.$

Si l'origine du système de coordonnées est choisi pour coïncider avec le sommet d, puis d = 0, de sorte que

$V = \ frac {| \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}) |} {6},$

où a, b, et c représentent trois arêtes qui se rencontrent à un sommet, et 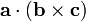$\ Mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c})$ est un triple produit scalaire. En comparant cette formule avec celle utilisée pour calculer le volume d'un parallélépipède, nous concluons que le volume d'un tétraèdre est égal à 1/6 du volume du parallélépipède quelconque qui partage avec lui trois bords convergents.

Il convient de noter que la triple scalaire peut être représenté par les déterminants suivants:

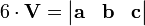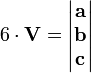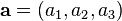$6 \ cdot \ mathbf {V} = \ begin {vmatrix} \ mathbf {a} et \ mathbf {b} et \ mathbf {c} \ end {} vmatrix$ ou $6 \ cdot \ mathbf {V} = \ begin {vmatrix} \ mathbf {a} \\ \ mathbf {b} \\ \ mathbf {c} \ end {} vmatrix$ où $\ Mathbf {a} = (a_1, a_2, A_3) \,$ est exprimée en ligne ou vecteur colonne etc.

D'où

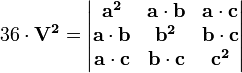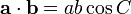$36 \ cdot \ mathbf {V ^ 2} = \ begin {vmatrix} \ mathbf {a ^ 2} et \ mathbf {a} \ cdot \ mathbf {b} et \ mathbf {a} \ cdot \ mathbf {c} \ \ \ mathbf {a} \ cdot \ mathbf {b} et \ mathbf {b ^ 2} et \ mathbf {b} \ cdot \ mathbf {c} \\ \ mathbf {a} \ cdot \ mathbf {c} et \ mathbf {b} \ cdot \ mathbf {c} et \ mathbf {c ^ 2} \ end {} vmatrix$ où $\ Mathbf {a} \ cdot \ mathbf {b} = ab \ cos {C}$ etc.

ce qui donne

$\ Mathbf {V} = \ frac {abc} {6} \ sqrt {1 + 2 \ cos {A} \ cos {b} cos {C} - \ ^ 2 cos {A} - \ cos ^ 2} {B - \ cos ^ 2 {C}} \,$

Si on nous donne seulement les distances entre les sommets de toute tétraèdre, alors nous pouvons calculer son volume en utilisant la formule:

$288 \ cdot V ^ 2 = \ begin {} vmatrix 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & d_ {12} ^ 2 & d_ {13} ^ 2 & d_ {14} ^ 2 \\ 1 & d_ {21} ^ 2 & 0 & d_ {23} ^ 2 & d_ {24} ^ 2 \\ 1 & d_ {31} ^ 2 & d_ {32} ^ 2 & 0 & d_ {34} ^ 2 \ \ 1 & d_ {41} ^ 2 & d_ {42} ^ 2 & d_ {43} ^ 2 & 0 \ end {} vmatrix.$

Si la valeur du facteur est négatif, cela signifie que nous ne pouvons pas construire un tétraèdre avec les distances indiquées entre les sommets.

Distance entre les bords

Les deux bords opposés de mensonge tétraèdre sur deux lignes obliques. Si la paire de points le plus proche entre ces deux lignes sont des points dans les bords, ils définissent la distance entre les bords; autrement, la distance entre les bords est égale à celle entre l'une des extrémités et le bord opposé.

Trois caractéristiques dimensionnelles d'un tétraèdre généralisée

Comme avec la géométrie de triangle, il ya un ensemble similaire de trois propriétés géométriques dimensionnelles pour un tétraèdre. Un tétraèdre généralisée a un insphere, circonscrite, tétraèdre et exspheres médial. Il dispose de centres respectifs tels que InCenter, circonscrit, excentriques, Centre Spieker et des points tels qu'un centre de gravité. Cependant, il est, en général, pas orthocenter dans le sens de courbes se croisent. Il se agit d'une sphère équivalente à la triangulaire neuf virgule cercle qui est le circonscrite du tétraèdre médial. Cependant, son circonscrite ne est pas, en général, passent par les points des hauteurs du tétraèdre de référence de base.

Pour résoudre ces incohérences, un centre de substitut connu comme le point Monge qui existe toujours un tétraèdre généralisée est introduit. Ce point a d'abord été identifié par Gaspard Monge. Pour tétraèdres où l'altitude ne se croisent, le point Monge et coïncident orthocentre. Le point Monge est à définir comme le point où les six plans médians d'un tétraèdre croisent. Un fond de panier central est défini comme un plan qui est orthogonal à un bord joignant deux sommets qui contient également le centre de gravité d'un bord opposé formé en joignant les deux autres sommets.

Une ligne a chuté orthogonale du point Monge à ne importe quel visage est coplanaire avec deux autres lignes orthogonales à la même face. La première est une altitude chuté d'un sommet correspondant à la face choisie. La seconde est une ligne orthogonale à la face choisie qui passe par l'orthocentre de ce visage. Cette ligne orthogonale par le point Monge se trouve à mi-chemin entre l'altitude et la ligne orthogonale orthocentrique.

Le Monge stade, centre de gravité et circonscrit d'un tétraèdre sont colinéaires et forment la ligne d'Euler du tétraèdre. Cependant, contrairement au triangle, le centre de gravité d'un tétraèdre est au milieu de son point et circonscrit Monge.

Il est une sphère équivalente à la triangulaire cercle de neuf points pour le tétraèdre généralisée. Ce est le circonscrite de son tétraèdre médial. Ce est une sphère en douze points centré sur le cercle circonscrit du tétraèdre médial. Par définition, elle passe à travers les centres de gravité des quatre faces du tétraèdre de référence. Il passe à travers quatre points de substitution d'Euler qui sont situés à une distance de 1/3 de la distance entre M, le point Monge, vers chacun des quatre sommets. Enfin, il passe à travers les quatre points de lignes orthogonales de base ont chuté de chaque point d'Euler sur le visage ne contenant pas le sommet qui a généré le point Euler.

Si T représente ce centre en douze points, alors il se trouve également sur la ligne d'Euler, contrairement à son homologue triangulaire, le centre se trouve un tiers de la distance entre M, le point Monge vers le cercle circonscrit. Par ailleurs, une ligne orthogonale à T à une face choisie est coplanaire avec deux autres lignes orthogonales à la même face. La première est une ligne orthogonale passant par le point Euler correspondant à la face choisie. La seconde est une ligne orthogonale passant par le centre de gravité de la face choisie. Cette ligne orthogonale à travers le centre de douze point se trouve à mi-chemin entre la ligne orthogonale point Euler et la ligne orthogonale centres de gravité. En outre, pour ne importe quel visage, le centre de douze points est au point médian du point Euler correspondant et l'orthocentre pour ce visage.

Le rayon de la sphère douze points est 1/3 du rayon circonscrit du tétraèdre de référence.

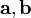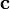Si OABC forme un tétraèdre généralisée avec un sommet O comme origine et vecteurs $\ Mathbf {a}, \ mathbf {b} \,$ et $\ Mathbf {c} \,$ représenter les positions des sommets A, B et C par rapport à O, alors le rayon de la insphere est donnée par:

$r = \ frac {} {6V | \ mathbf {b} \ times \ mathbf {c} | + | \ mathbf {c} \ fois \ mathbf {a} | + | \ mathbf {a} \ times \ mathbf {b } | + | (\ mathbf {b} \ times \ mathbf {c}) + (\ mathbf {c} \ times \ mathbf {a}) + (\ mathbf {a} \ times \ mathbf {b}) |} \,$

et le rayon de la sphère circonscrite est donnée par:

$R = \ frac {| \ mathbf {a ^ 2} (\ mathbf {b} \ times \ mathbf {c}) + \ mathbf {b ^ 2} (\ mathbf {c} \ times \ mathbf {a}) + \ mathbf {c ^ 2} (\ mathbf {a} \ times \ mathbf {b}) |} {12V} \,$

ce qui donne le rayon de la sphère de douze points:

$R_T = \ frac {| \ mathbf {a ^ 2} (\ mathbf {b} \ times \ mathbf {c}) + \ mathbf {b ^ 2} (\ mathbf {c} \ times \ mathbf {a}) + \ mathbf {c ^ 2} (\ mathbf {a} \ times \ mathbf {b}) |} {36V} \,$

où:

$6V = | \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}) | \,$

La position de vecteur de différents centres sont donnés comme suit:

Le centroïde

$\ Mathbf {G} = \ frac {\ mathbf {a} + \ mathbf {b} + \ mathbf {c}} {4} \,$

Le cercle circonscrit

$\ Mathbf {O} = \ frac {\ mathbf {a ^ 2} (\ mathbf {b} \ times \ mathbf {c}) + \ mathbf {b ^ 2} (\ mathbf {c} \ times \ mathbf {a }) + \ mathbf {c ^ 2} (\ mathbf {a} \ times \ mathbf {b})} {12V} \,$

Le point Monge

$\ Mathbf {M} = \ frac {\ mathbf {a} \ cdot (\ mathbf {b} + \ mathbf {c}) (\ mathbf {b} \ times \ mathbf {c}) + \ mathbf {b} \ cdot (\ mathbf {c} + \ mathbf {a}) (\ mathbf {c} \ times \ mathbf {a}) + \ mathbf {c} \ cdot (\ mathbf {a} + \ mathbf {b}) ( \ mathbf {a} \ times \ mathbf {b})} {12V} \,$

Les relations de la ligne d'Euler sont:

$\ Mathbf {G} = \ mathbf {M} + \ frac {1} {2} (\ mathbf {O} - \ mathbf {M}) \,$

$\ Mathbf {T} = \ mathbf {M} + \ frac {1} {3} (\ mathbf {O} - \ mathbf {M}) \,$

Il convient également de noter ce qui suit:

$\ Mathbf {a} \ cdot \ mathbf {O} = \ frac {\ mathbf {a ^ 2}} {2} \ quad \ quad \ mathbf {b} \ cdot \ mathbf {O} = \ frac {\ mathbf { b ^ 2}} {2} \ quad \ quad \ mathbf {c} \ cdot \ mathbf {O} = \ frac {\ mathbf {c ^ 2}} {2} \,$

et:

$\ Mathbf {a} \ cdot \ mathbf {M} = \ frac {\ mathbf {a} \ cdot (\ mathbf {b} + \ mathbf {c})} {2} \ quad \ quad \ mathbf {b} \ cdot \ mathbf {M} = \ frac {\ mathbf {b} \ cdot (\ mathbf {c} + \ mathbf {a})} {2} \ quad \ quad \ mathbf {c} \ cdot \ mathbf {M} = \ frac {\ mathbf {c} \ cdot (\ mathbf {a} + \ mathbf {b})} {2} \,$

Relations géométriques

Un tétraèdre est un 3- simplex. Contrairement au cas d'autres solides de Platon, tous les sommets d'un tétraèdre régulier sont équidistantes l'une de l'autre (elles sont à la seule disposition possible de quatre points équidistants).

A est un tétraèdre triangulaire pyramide, et le tétraèdre régulier est auto-double.

Un tétraèdre régulier peut être intégré à l'intérieur d'un cube de deux manières de telle sorte que chaque sommet est un sommet du cube, et chaque bord est une diagonale de l'une des faces du cube. Pour une telle intégration, la coordonnées cartésiennes de la les sommets sont

(1, 1, 1);

(-1, -1, 1);

(-1, +1, -1);

(1, -1, -1).

Pour l'autre tétraèdre (qui est double à la première), inverser tous les signes. Le volume de ce tétraèdre est 1/3 du volume du cube. Combinant à la fois tétraèdres donne une régulière composé polyédrique appelé stella octangula, dont l'intérieur est un octaèdre . De manière correspondante, un octaèdre régulier est le résultat de couper, d'un tétraèdre régulier, quatre tétraèdres réguliers de la moitié de la taille linéaire (c.-à- redresser le tétraèdre). L'enrobage ci-dessus divise le cube en cinq tétraèdres, dont l'un est régulière. En fait, la figure 5 est le nombre minimum de tétraèdres nécessaire pour composer un cube.

L'inscription tétraèdres l'intérieur de la régulière composé de cinq cubes donne deux composés plus réguliers, contenant cinq et dix tétraèdres.

Tétraèdres réguliers ne peuvent pas espace tessellate par eux-mêmes, même se il semble assez probable que Aristote a rapporté qu'il était possible. Cependant, deux tétraèdres réguliers peut être combiné avec un octaèdre, ce qui donne un rhomboèdre qui peuvent espace de tuile.

Cependant, il ya au moins un tétraèdre irrégulier dont des copies peuvent espace de tuile. Si l'on détend l'exigence selon laquelle les tétraèdres être tous de la même forme, il est possible de l'espace de carreaux en utilisant seulement des tétraèdres de diverses manières. Par exemple, on peut diviser un octaèdre en quatre tétraèdres identiques et de les combiner à nouveau avec deux les réguliers. (Comme un side-note: ces deux types de tétraèdre ont le même volume.)

Le tétraèdre est unique parmi les polyèdres uniformes de posséder aucun faces parallèles.

Polyèdres connexes

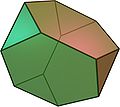
Tétraèdre tronqué
Deux tétraèdres dans un cube
Composé de cinq tétraèdres
Composé de dix tétraèdres

Tétraèdres coupant

Un polyèdre intéressante peut être construit à partir de cinq tétraèdres intersection. Cette composé de cinq tétraèdres est connu depuis des centaines d'années. Il revient régulièrement dans le monde de origami. Rejoindre les vingt sommets formerait un régulière dodécaèdre. Il existe à la fois gaucher et formes droitiers qui sont des images spéculaires l'une de l'autre.

Les isométries du tétraèdre régulier

Les rotations et des réflexions appropriés dans le groupe de symétrie du tétraèdre régulier

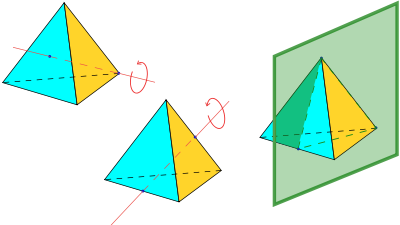
Les sommets d'un cube peuvent être regroupées en deux groupes de quatre, chacun formant un tétraèdre régulier (voir ci-dessus, et également animation, montrant l'un des deux tétraèdres dans le cube). Les symétries d'un tétraèdre régulier correspondent à la moitié de celle d'un cube: ceux qui cartographier les tétraèdres à eux-mêmes, et non à l'autre.

Le tétraèdre est le seul solide platonicien qui ne est pas mappé à lui-même par le point d'inversion.

Le tétraèdre régulier a 24 isométries, formant le groupe de symétrie _{T d,} isomorphe à S _4. Ils peuvent être classés comme suit:

T, isomorphe à groupe alterné A ₄ (l'identité et 11 rotations appropriées) par le suivant classes de conjugaison (entre parenthèses sont donnés les permutations des sommets, ou en conséquence, les visages, et la Unité représentation de quaternion):
- identité (identité; 1)
- rotation autour d'un axe passant par un sommet, perpendiculaire au plan opposé, d'un angle de ± 120 °: 4 axes, chaque axe 2, ainsi que 8 ((1 2 3), etc .; (i ± 1 ± j ± k) / 2)
- rotation d'un angle de 180 ° de sorte qu'un bord de carte au bord opposé 3: ((1 2) (3 4), etc .; i, j, k)
réflexions dans un plan perpendiculaire à un bord 6:
de réflexions dans un plan combiné avec rotation de 90 ° autour d'un axe perpendiculaire au plan 3: deux axes, chaque axe, ainsi que 6; de façon équivalente, ils sont 90 ° rotations combinées avec inversion (x est mappé à - x): les rotations correspondent à celles du cube autour d'axes en face-à-face

Les isométries de tétraèdres irrégulière

Les isometries d'un tétraèdre irrégulier dépendent de la géométrie du tétraèdre, avec sept cas possible. Dans chaque cas, un Groupe de points en 3 dimensions est formé.

Une base triangle équilatéral et isocèle (et non équilatéral) côtés du triangle donne six isométries, correspondant aux six isométries de la base. Comme permutations des sommets, ces six isométries sont l'une identité (123), (132), (12), (13) et (23), formant le groupe de symétrie C _3v, isomorphe à S _3.
Quatre isocèle congruents (non-équilatéraux) triangles donne huit isométries. Si les bords (1,2) et (3,4) sont de longueur différente de celle des quatre autres puis 8 isométries sont l'une identité, des réflexions (12) et (34), et des rotations de 180 ° (12) (34), (13) (24) (14) (23) et irrégulières rotations de 90 ° (1234) et (1432) formant le groupe de symétrie D _2d.
Quatre triangles scalènes congruents donne quatre isométries. Les isometries sont 1 et les rotations de 180 ° (12) (34) (13) (24) (14) (23). Ceci est le Klein-quatre groupes V ≅ _{4 ² 2} Z, présent en tant que groupe de points D _2.
Deux paires de isocèle isomorphes (non-équilatéraux) triangles. On obtient ainsi deux bords opposés (1,2) et (3,4) qui sont perpendiculaires mais longueurs différentes, et ensuite les quatre isométries sont 1, des réflexions (12) et (34) et la rotation de 180 ° (12) (34) . Le groupe de symétrie est C _2v, isomorphe à V _4.
Deux paires de triangles scalènes isomorphes. Cela a deux paires d'arêtes égales (1,3), (2,4) et (1,4), (2,3), mais sinon pas d'arêtes égales. Les deux seuls sont une isométrie et la rotation (12) (34), ce qui donne le groupe C ₂ isomorphe à Z _2.
Deux isocèle inégales triangles avec une base commune. Cela a deux paires d'arêtes égales (1,3), (1,4) et (2,3), (2,4) et autrement sans arêtes égales. Les deux seuls isometries sont 1 et la réflexion (34), ce qui donne le groupe C _s isomorphe à Z _2.
Aucun bords égales, de sorte que la seule isométrie est l'identité, et le groupe de symétrie est le groupe trivial.

Une loi des sinus pour tétraèdres et l'espace de toutes les formes de tétraèdres

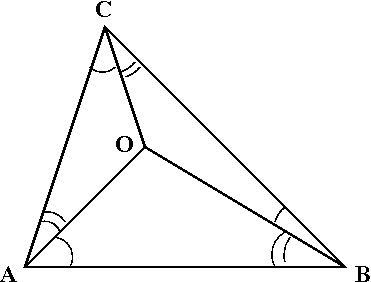
Un corollaire de l'habituel loi des sinus est que, dans un tétraèdre dont les sommets sont O, A, B, C, nous avons

$\ Sin \ angle OAB \ cdot \ sin \ angle OBC \ cdot \ sin \ angle OCA = \ sin \ angle CAO \ cdot \ sin \ angle OCB \ cdot \ sin \ angle OBA. \,$

On peut voir les deux côtés de cette identité comme correspondant à droite et à gauche orientations de la surface.

Mettre l'un des quatre sommets dans le rôle de O donne quatre de ces identités, mais dans un sens au plus trois d'entre eux sont indépendants: Si les "droite" côtés de trois d'entre eux sont multipliés et le produit est déduit pour être égale à la produit des côtés "antihoraire" des trois mêmes identités, puis facteurs communs sont annulés à partir des deux côtés, le résultat est le quatrième identité. Une raison d'être intéressé par cet «indépendance» relation est ceci: Il est bien connu que trois angles sont les angles de certaines triangle si et seulement si leur somme est un demi-cercle. Dans quel état sur 12 angles est nécessaire et suffisante pour qu'ils soient les 12 angles de certains tétraèdre? Il est clair que la somme des angles de ne importe quel côté du tétraèdre doit être un demi-cercle. Comme il existe quatre de ces triangles, il existe quatre de ces contraintes sur les montants d'angles, et le nombre de degrés de liberté est ainsi réduite de 12 à 8. Les quatre relations données par la loi sinusoïdale de réduire davantage le nombre de degrés de liberté, et non vers le bas de 8 à 4, mais seulement à partir de 8 jusqu'à 5, étant donné que la quatrième contrainte ne est pas indépendant des trois premiers. Ainsi, l'espace de toutes les formes de tétraèdres est 5 dimensions.

Utilisations de calcul

Formes complexes sont souvent décomposés en une filet de tétraèdres irrégulière en vue de l'analyse des éléments finis et calcul des études de dynamique des fluides.

Applications et utilisations

Le ion ammonium est tétraédrique

Plusieurs des pièces Tetrahedron de notation et les objectifs de la 2005 FIRST Robotics jeu

Conditionnement

L'entreprise Tetra Classic Tetrapak est sous la forme d'un tétraèdre.

Chimie

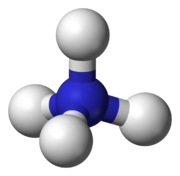
La forme de tétraèdre est vu dans la nature des liaisons covalentes des molécules. Par exemple, dans un méthane molécule (CH _4), les quatre atomes d'hydrogène se trouvent dans chaque coin d'un tétraèdre avec l'atome de carbone dans le centre. Pour cette raison, l'une des principales revues en chimie organique est appelé Tetrahedron. Ammonium est un autre exemple.
Angle du centre vers deux sommets est 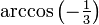$\ arccos {\ left (- \ frac {1} {3} \ right)}$ , soit environ 109,47 °.

Électronique

Si chaque bord d'un tétraèdre devait être remplacé par un ohm résistance, la résistance entre deux sommets serait 2.1 ohm.

Symbolisme

Le tétraèdre représente l'élément classique feu.

Jeux

Surtout dans jeu de rôle, ce solide est connu comme un d4 , l'un des plus courants dés polyédriques .
Tétraèdres construits de 1 1/4 " Tuyau en PVC, qui ont été connu comme «tétras», ont été utilisés comme l'objet de notation principale sur le 2005 FIRST Robotics jeu Triple Play. Le but du jeu est d'empiler ces «tétras» sur des objectifs plus larges de tétraèdre dont voici placés dans une matrice 3 × 3.
Certains Cube de Rubik les puzzles sont tétraédrique, comme le Pyraminx et Pyramorphix.
La tête de la Pyramide Silent Hill jeux a un tétraèdre sur le dessus de sa tête.

Fiction

Dans le Séquence de Xeelee livres de science-fiction de l'auteur Stephen Baxter, un tétraèdre bleu-vert est le symbole de l'humanité libre.
Le Triforces du Legend of Zelda série de dessins animés sont des tétraèdres verts et rouges. La représentation de la Triforce de la série de jeu réel (à partir de A Link to the Past) est celle d'un tétraèdre déplié.
L'arc de la série de fan "Star Trek histoire: Invisible Frontier "évolue anciens artefacts autour gigantesques, qui deviennent plus tard une partie centrale de la série. Les artefacts sont dénommé Tetrahedrons et ont la forme d'un tel organisme géométrique. Dans la série, les tétraèdres possèdent la capacité de produire une grande de l'énergie et sont de matériau inconnu et l'origine, cependant, ils semblent être vieux de plusieurs millions d'années et il est souligné que ces appareils ont été construits par une civilisation ancienne.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Tetrahedron&oldid=205612904 "

We provide Linux to the World