
Les fonctions trigonométriques
À propos de ce écoles sélection Wikipedia
Cette sélection écoles a été choisi par SOS Enfants pour les écoles dans le monde en développement ne ont pas accès à Internet. Il est disponible en téléchargement intranet. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .
| Fonction | Abréviation | Les identités (en utilisant radians ) |
|---|---|---|
| Sinus | péché | 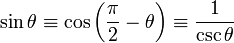 |
| Cosinus | cos | 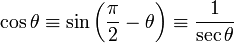 |
| Tangente | bronzage (Ou Tg) | 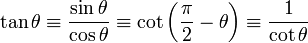 |
| Cosécante | csc (Ou COSEC) | 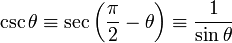 |
| Sécante | seconde | 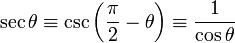 |
| Cotangente | lit d'enfant (Ou CTG ou CTN) | 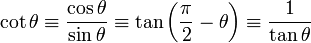 |
En mathématiques , les fonctions trigonométriques (également appelées fonctions circulaires) sont les fonctions d'un angle . Ils jouent un rôle important dans l' étude de triangles et de modélisation phénomènes périodiques, parmi beaucoup d'autres applications. Les fonctions trigonométriques sont communément définis comme rapports de deux côtés d'un triangle rectangle contenant l'angle, et peut être équivalente définis comme les longueurs des différents segments de ligne à partir d'un cercle unité. Plus de définitions modernes de les exprimer au série infinie ou sous forme de solutions de certaines équations différentielles , permettant leur extension à des valeurs positives et négatives arbitraires et même à des nombres complexes .
Dans l'usage moderne, il ya six fonctions trigonométriques de base, qui sont ensuite présentés ici avec les équations relatives à une autre. Surtout dans le cas des quatre derniers, ces relations sont souvent considérés comme les définitions de ces fonctions, mais on peut les définir aussi bien géométriquement ou par d'autres moyens, puis dériver ces relations.
Histoire
La notion qu'il devrait y avoir une correspondance standard entre la longueur des côtés d'un triangle et les angles du triangle vient dès que l'on admet que les triangles semblables maintiennent les mêmes rapports entre leurs côtés. Autrement dit, pour chaque triangle similaire, le rapport de l'hypoténuse (par exemple) et un autre des côtés reste le même. Si l'hypoténuse est deux fois plus longtemps, sont donc les côtés. Ce est seulement ces rapports que les fonctions trigonométriques expriment.
Les fonctions trigonométriques ont été étudiés par Hipparque de Nicée (180 à 125 avant JC), Ptolémée d' Egypte (90-180 AD), Aryabhata (476-550), Varahamihira, Brahmagupta, Muhammad ibn Musa al-Ḵwārizmī , Abu al-Wafaa Al-Būzjānī, Omar Khayyam, Bhāskara II, Nasir al-Din al-Tusi, Ghiyath al-Kashi (14ème siècle), Ulugh Beg (14ème siècle), Regiomontanus (1464), Rheticus et Rheticus de l'étudiant Valentin Otho.
Madhava de Sangamagramma (c. 1400) a fait des progrès rapides dans l' analyse des fonctions trigonométriques en termes de série infinie. Leonhard Euler Introductio s 'en analysin infinitorum (1748) était principalement chargé d'établir le traitement analytique des fonctions trigonométriques en Europe, aussi les définir série comme infini et présentant " La formule d'Euler ", ainsi que les abréviations péché quasi-moderne., Cos., Tang., Lit bébé., Sec., Et COSEC.
Quelques fonctions sont communes historiquement (et apparaissent dans les premières tables), mais sont désormais rarement utilisés, tels que le accord (CRD (θ) = 2 sin (θ / 2)), le Versine (versin (θ) = 1 - cos (θ) = 2 sin² (θ / 2)), le Haversine (Haversin (θ) = versin (θ) / 2 = sin² (θ / 2)), le exsecant (exsec (θ) = s (θ) - 1) et le excosecant (excsc (θ) = exsec (π / 2 - θ) = csc (θ) - 1). Beaucoup plus de relations entre ces fonctions sont énumérées dans l'article sur identités trigonométriques.
Définitions triangle rectangle
| Trigonométrie |
|---|
| Histoire Usage Fonctions Généralisé Fonctions inverses Pour en savoir plus |
| Référence |
| Identités Constantes précises Tables trigonométriques |
| Lois et théorèmes |
| Loi des sinus Loi des cosinus Loi des tangentes Loi de cotangentes Théorème de Pythagore |
| Calcul |
| Substitution trigonométrique Intégrales de fonctions Dérivées des fonctions Intégrales de fonctions inverses |
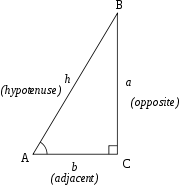
Afin de définir les fonctions trigonométriques de l'angle A, commencer avec un arbitraire triangle qui contient l'angle A:
Nous utilisons les noms suivants pour les côtés du triangle:
- Le hypoténuse est le côté opposé à l'angle droit, ou défini comme le côté le plus long d'un triangle rectangle, dans ce cas h.
- Le côté opposé est le côté opposé à l'angle qui nous intéresse, dans ce cas un.
- Le côté adjacent est le côté qui est en contact avec l'angle qui nous intéresse et l'angle droit, d'où son nom. Dans ce cas, le côté adjacent est b.
Tous les triangles sont prises pour exister dans le plan euclidien sorte que les angles à l'intérieur de chaque montant en forme de triangle à π radians (ou 180 ° ); Par conséquent, pour un triangle rectangle des deux angles non-droits sont compris entre zéro et π / 2 radians (ou 90 ° ). Le lecteur doit noter que les définitions suivantes, à proprement parler, ne définissent les fonctions trigonométriques pour les angles de cette gamme. Nous les étendre à l'ensemble des arguments réels en utilisant le cercle unité, ou en exigeant certaines symétries et qu'ils soient des fonctions périodiques.
1) Le sinus d'un angle est le rapport de la longueur du côté opposé à la longueur de l'hypoténuse. Dans notre cas
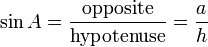 .
.
Notez que ce ratio ne dépend pas du triangle droit particulier choisi, tant qu'il contient de l'angle A, puisque tous ces triangles sont similaire.
L'ensemble des zéros de sinus (ie, les valeurs de  pour lequel
pour lequel 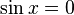 ) Est
) Est
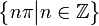 .
.
2) le cosinus d'un angle est le rapport entre la longueur du côté adjacent à la longueur de l'hypoténuse. Dans notre cas
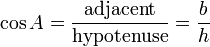 .
.
L'ensemble des zéros de cosinus
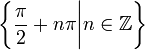 .
.
3) La tangente de l'angle est le rapport entre la longueur du côté opposé à la longueur du côté adjacent. Dans notre cas
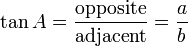 .
.
L'ensemble des zéros de tangente est
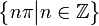 .
.
Le même ensemble de la fonction sinus depuis
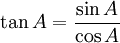 .
.
Les trois autres fonctions sont mieux définies en utilisant les trois fonctions ci-dessus.
4) Le cosécante csc (A) est le inverse multiplicatif de sin (A), ce est à dire le rapport de la longueur de l'hypoténuse de la longueur du côté opposé:
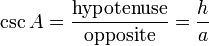 .
.
5) Le sec sécant (A) est le inverse multiplicatif de cos (A), ce est à dire le rapport de la longueur de l'hypoténuse de la longueur du côté adjacent:
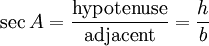 .
.
6) La cotangente lit (A) est le inverse multiplicatif de tan (A), ce est à dire le rapport entre la longueur du côté adjacent à la longueur de l'autre côté:
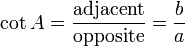 .
.
définitions de pente
Equivalent aux définitions droit triangle, les fonctions trigonométriques peuvent être définies en termes de hausse, Exécuter, pente d'un segment de ligne par rapport à une ligne horizontale. La pente est souvent enseigné comme "montée sur la distance" ou hausse / run. Les trois principales fonctions trigonométriques sont couramment enseignés dans l'ordre sinus, cosinus, tangente. Avec un cercle unité, la correspondance suivante existe des définitions:
- Sine est le premier, est le premier lieu. Sine prend un angle et raconte la montée.
- Cosinus est seconde, terme est deuxième. Cosinus prend un angle et raconte la course.
- Tangent est la formule de la pente qui combine la montée et la course. Tangent prend un angle et raconte la pente.
Cela montre l'utilisation principale de la tangente et arctangente: la conversion entre les deux façons de raconter l'inclinaison d'une ligne, ce est à dire, les angles et les pentes. (Notez que l'arctangente ou «tangente inverse" ne doit pas être confondu avec la cotangente, qui est cos divisé par le péché.)
Alors que le rayon du cercle ne fait aucune différence pour la pente (la pente ne dépend pas de la longueur de la ligne oblique), elle ne affecte pas montée et exécuté. Pour adapter et de trouver la hausse réelle et courir, il suffit de multiplier le sinus et cosinus par le rayon. Par exemple, si le cercle a un rayon de 5, la course à un angle de 1 ° est 5 cos (1 °)
Définitions Unité-cercle
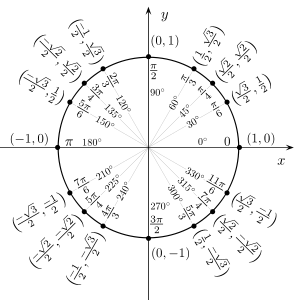
Les six fonctions trigonométriques peuvent également être définies en termes de cercle unité, le cercle de rayon une centrée à l'origine. La définition de cercle unité fournit peu à la manière de calcul pratique; En effet, il se appuie sur des triangles rectangles pour la plupart des angles. La définition de cercle unité ne permet toutefois la définition des fonctions trigonométriques pour tous les arguments positifs et négatifs, et pas seulement pour des angles entre 0 et π / 2 radians. Il fournit également une seule image visuelle qui encapsule à la fois tous les triangles importants. Du théorème de Pythagore l'équation pour le cercle unité est:
Sur la photo, quelques angles communs, mesurée en radians, sont donnés. Mesures dans le sens inverse des aiguilles d'une montre sont des angles positifs et des mesures dans le sens horaire sont des angles négatifs. Laissez une ligne passant par l'origine, faisant un angle de θ avec la moitié positive du cercle axe x intersection de l'appareil. Les x - et y -coordinates de ce point d'intersection sont égaux à cos θ et sin θ, respectivement. Le triangle dans le graphique applique la formule; le rayon est égal à l'hypoténuse et a une longueur de 1, donc nous avons péché θ = y / 1 et cos θ = x / 1. Le cercle unité peut être considéré comme un moyen de regarder un nombre infini de triangles en faisant varier la longueur de leurs jambes, mais en gardant les longueurs de leurs hypoténuses égal à 1.
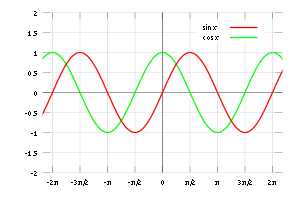
Pour des angles supérieurs à 2π ou moins de -2π, il suffit de continuer à tourner autour du cercle. De cette manière, le sinus et le cosinus devient fonctions périodiques avec la période 2π:
pour ne importe quel angle θ et tout entier k.
La plus petite période positive d'une fonction périodique est appelée la période primitive de la fonction. La période primitive du sinus, cosinus, sécante ou cosécante est un cercle complet, soit 2π radians ou 360 degrés; la période primitive de la tangente ou cotangente est seulement un demi-cercle, soit π radians ou 180 degrés. Ci-dessus, seulement sinus et cosinus sont définis directement par le cercle unité, mais les quatre autres fonctions trigonométriques peuvent être définis par:
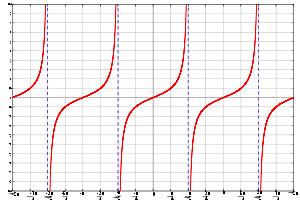
Pour le droit est une image qui affiche un graphique sensiblement différente de la fonction trigonométrique f (θ) = tan (θ) graphiquement sur le plan cartésien. Notez que ses abscisses à l'origine correspondent à celle du péché (θ), tandis que ses valeurs non définies correspondent aux abscisses à l'origine des cos θ (). Observer que les résultats de la fonction changent lentement autour des angles de k π, mais changent rapidement à des angles proches de (k + 1/2) π. Le graphe de la fonction tangente verticale a également un asymptote à θ = (k + 1/2) π. Ce est le cas parce que la fonction tend vers l'infini que θ approches (k + 1/2) π de la gauche et moins l'infini à l'approche (k + 1/2) π de la droite.
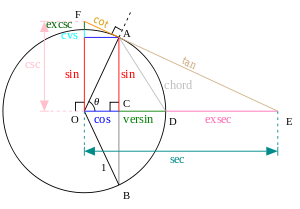
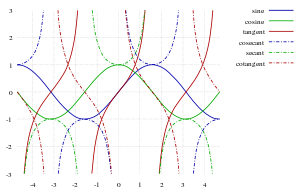
Sinon, toutes les fonctions trigonométriques de base peut être défini en termes d'un cercle unité centré à O (illustré à droite, vers le haut de la page), et ces définitions géométriques semblables ont été utilisés historiquement. En particulier, pour une corde AB du cercle, où θ est la moitié de l'angle sous-tendu, sin (θ) est AC (la moitié de la corde), une définition introduite en Inde (voir ci-dessus). cos (θ) est l'OC de distance horizontale, et versin (θ) = 1 - cos (θ) est CD. tan (θ) est la longueur du segment AE de la tangente par A, d'où le mot tangente pour cette fonction. lit bébé (θ) est un autre segment de la tangente, AF. s (θ) = OE et csc (θ) = sont des segments de droites sécantes (coupant le cercle en deux points), et peuvent également être considérés comme des projections de l'arthrose long de la tangente en A aux axes horizontaux et verticaux, respectivement. DE est exsec (θ) = s (θ) - 1 (la partie de la sécante extérieur, ou ex, le cercle). De ces constructions, il est facile de voir que les fonctions de sécantes et tangente divergent θ approches π / 2 (90 degrés) et que la cosécante et la cotangente divergent θ tend vers zéro. (Beaucoup de constructions similaires sont possibles, et les identités trigonométriques de base peuvent également être prouvés graphique.)
définitions de la série
En utilisant seulement la géométrie et les propriétés des limites , il peut être démontré que le dérivé de sinus cosinus et est dérivé de cosinus est le négatif de sinus. (Ici, et plus généralement dans le calcul , tous les angles sont mesurés en radians ; voir également l'importance de radians ci-dessous.) On peut alors utiliser la théorie de la série de Taylor de montrer que les identités suivantes sont valables pour tous les nombres réels x:
Ces identités sont souvent considérés comme les définitions de la fonction sinus et cosinus. Ils sont souvent utilisés comme point de départ d'un traitement rigoureux des fonctions trigonométriques et leurs applications (par exemple, dans série de Fourier), depuis la théorie de série infinie peut être élaboré à partir des fondements de la système de nombre réel , indépendamment de toutes considérations géométriques. Le différentiabilité et la continuité de ces fonctions sont ensuite établi à partir des définitions de la série seuls.
Autre série peut être trouvé:
où
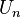 est la n ième haut / bas nombre,
est la n ième haut / bas nombre, 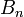 est la n ième Nombre de Bernoulli, et
est la n ième Nombre de Bernoulli, et 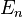 (Ci-dessous) est le n ième Nombre d'Euler.
(Ci-dessous) est le n ième Nombre d'Euler.
Lorsque cela est exprimé dans une forme dans laquelle les dénominateurs sont les factorielles correspondantes, et les numérateurs, appelé "numéros tangents", ont une combinatoire interprétation: ils énumèrent permutations alternées de ensembles finis de cardinalité impaire.
Lorsque cela est exprimé dans une forme dans laquelle les dénominateurs sont les factorielles correspondant, les numérateurs, appelés les "numéros" sécantes, ont une combinatoire interprétation: ils énumèrent permutations alternées de ensembles finis de même cardinal.
De un théorème analyse complexe, il existe un prolongement analytique unique de cette fonction réelle pour les nombres complexes. Ils ont la même série de Taylor, et ainsi les fonctions trigonométriques sont définis sur les nombres complexes en utilisant la série de Taylor ci-dessus.
Relation à la fonction exponentielle et nombres complexes
Il peut être démontré par les définitions de la série que les fonctions sinus et cosinus sont les imaginaires et réels parties, respectivement, de la fonction exponentielle complexe lorsque son argument est purement imaginaire:
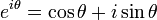 .
.
Cette identité est appelée La formule d'Euler. De cette façon, les fonctions trigonométriques deviennent essentiels dans l'interprétation géométrique d'analyse complexe. Par exemple, avec l'identité ci-dessus, si l'on considère le cercle unité dans le plan complexe , définie par e i x, et comme ci-dessus, on peut paramétrer ce cercle en fonction de cosinus et de sinus, le rapport entre l'exponentielle complexe et la trigonométrique fonctions devient plus apparente.
En outre, cela permet la définition des fonctions trigonométriques pour les arguments complexes z:
où i 2 = -1. Aussi, pour des raisons purement réel x,
Il est également connu que les processus exponentielles sont intimement liés au comportement périodique.
Définitions via des équations différentielles
Les deux fonctions sinus et cosinus satisfont à l' équation différentielle
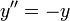 .
.
Ce est-à-dire, chacun est le négatif de son propre dérivé seconde. Dans le deux dimensions un espace de réception V constitué par les solutions de cette équation, la fonction sinus est l'unique solution satisfaisant aux conditions initiales y (0) = 0 et y '(0) = 1, et la fonction cosinus est l'unique solution satisfaisant aux conditions initiales y (0) = 1 et y '(0) = 0. Etant donné que les fonctions sinus et cosinus sont linéairement indépendantes, ensemble, ils forment un base de V. Cette manière de définir les fonctions sinus et cosinus est essentiellement équivalente à l'aide de la formule d'Euler. (Voir équation différentielle linéaire.) Il se avère que cette équation différentielle peut être utilisé non seulement pour définir les fonctions sinus et cosinus, mais aussi pour prouver la identités trigonométriques pour les fonctions sinus et cosinus. En outre, l'observation que les sinus et cosinus satisfait 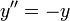 signifie qu'ils sont fonctions propres de la dérivée seconde opérateur.
signifie qu'ils sont fonctions propres de la dérivée seconde opérateur.
La fonction tangente est l'unique solution de l'équation différentielle non linéaire
satisfaisant à la condition initiale y (0) = 0. Il existe une preuve visuelle très intéressant de noter que la fonction tangente satisfait à cette équation différentielle; voir Analyse Visual Complex de Needham.
L'importance de radians
Radians spécifier un angle de mesure de la longueur autour de la trajectoire du cercle unité et constituent un argument particulier pour les fonctions sinus et cosinus. En particulier, seuls les sinus et cosinus quelle carte radians ratios satisfont les équations différentielles qui décrivent classiquement eux. Si un argument en sinus et cosinus en radians est redimensionné par la fréquence,
alors les dérivés seront échelle par amplitude.
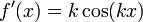 .
.
Ici, k est une constante qui représente une correspondance entre les unités. Si x est en degrés, puis
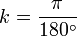 .
.
Cela signifie que la dérivée seconde de la condition sine en degrés satisfait pas à l'équation différentielle
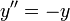 ,
,
mais plutôt
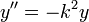 ;
;
dérivée seconde de cosinus se comporte de façon similaire.
Cela signifie que ces sinus et cosinus sont des fonctions différentes, et que le quatrième dérivé de sinus sinus seront de nouveau seulement si l'argument est en radians.
Identités
Beaucoup identités existent, qui interagissent les fonctions trigonométriques. Parmi les plus fréquemment utilisé est l'identité de Pythagore, qui stipule que, pour ne importe quel angle, le carré du sinus plus le carré du cosinus est toujours 1. Ce est facile de voir en étudiant un triangle droit de l'hypoténuse 1 et en appliquant le théorème de Pythagore . Dans une forme symbolique, l'identité de Pythagore lit,
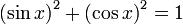 ,
,
qui est plus communément écrit avec l'exposant «deux» à côté du symbole de sinus et cosinus:
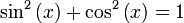 .
.
Dans certains cas, les parenthèses intérieures peuvent être omises.
D'autres relations clés sont la somme et la différence des formules qui donnent le sinus et cosinus de la somme et la différence des deux angles en termes de sinus et cosinus des angles eux-mêmes. Ceux-ci peuvent être dérivées géométriquement, en utilisant des arguments qui remontent à Ptolémée ; on peut aussi les produire algébrique en utilisant la formule d'Euler.
Lorsque les deux angles sont égaux, les formules de somme à réduire équations simples connus comme les formules angle double.
Ces identités peuvent également être utilisés pour dériver le identités produit-à-somme qui ont été utilisés dans l'antiquité pour transformer le produit de deux nombres en une somme de chiffres et d'accélérer considérablement les opérations, tout comme la fonction logarithme .
Calcul
Pour intégrales et dérivés de fonctions trigonométriques, voir les sections pertinentes du table des dérivés, table des intégrales, et liste des intégrales de fonctions trigonométriques. Voici la liste des dérivées et intégrales des six fonctions trigonométriques de base.
Définitions utilisant les équations fonctionnelles
Dans l'analyse mathématique , on peut définir les fonctions trigonométriques utilisant équations fonctionnelles basées sur des propriétés telles que les formules somme et de différence. En prenant comme donné ces formules ainsi que l'identité de Pythagore, par exemple, on peut prouver que seulement deux fonctions réelles remplissent ces conditions. Symboliquement, nous disons qu'il existe exactement une paire de fonctions réelles 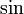 et
et 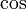 de telle sorte que pour tous les nombres réels x et y, les équations suivantes sont vérifiées:
de telle sorte que pour tous les nombres réels x et y, les équations suivantes sont vérifiées:
avec la condition supplémentaire que
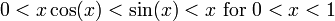 .
.
D'autres dérivations, à partir d'autres équations fonctionnelles sont également possibles, et de telles dérivations peuvent être étendus à des nombres complexes. A titre d'exemple, cette dérivation peut être utilisé pour définir la trigonométrie dans les champs de Galois.
Calcul
Le calcul de fonctions trigonométriques est un sujet complexe, qui, aujourd'hui, peut être évitée par la plupart des gens en raison de la grande disponibilité des ordinateurs et calculatrices scientifiques qui fournissent des fonctions intégrées trigonométriques pour ne importe quel angle. Dans cette section, cependant, nous décrivons plus de détails sur leur calcul dans trois contextes importants: l'utilisation historique de tables trigonométriques, les techniques modernes utilisées par les ordinateurs, et quelques angles «importants» où les valeurs exactes simples sont faciles à trouver. (Ci-dessous, il suffit de considérer une petite gamme d'angles, par exemple de 0 à π / 2, puisque tous les autres angles peuvent être réduits à cette gamme par la périodicité et les symétries des fonctions trigonométriques.)
Avant les ordinateurs, les gens généralement évalués fonctions trigonométriques par interpolation à partir d'un tableau détaillé de leurs valeurs, calculée à beaucoup chiffres significatifs. De telles tables sont disponibles pour aussi longtemps que les fonctions trigonométriques ont été décrits (voir histoire ci-dessus), et ont été typiquement généré par l'application répétée de la demi-angle et l'angle d'addition identités à partir d'une valeur connue (telles que sin (π / 2) = 1).
Les ordinateurs modernes utilisent une variété de techniques. Une méthode courante, en particulier sur les processeurs haut de gamme avec des unités à virgule flottante, est de combiner un polynôme ou rationnel approximation (tels que Chebyshev rapprochement, rapprochement plus bel uniforme, et Approximation de Padé, et généralement plus élevés pour les précisions ou variables, Taylor et Laurent série) avec réduction et une consultation de table - ils regardent d'abord jusqu'à l'angle le plus proche à une petite table, et ensuite utiliser le polynôme pour calculer la correction. Sur les appareils plus simples qui manquent multiplicateurs de matériel, il existe un algorithme appelé CORDIC (ainsi que des techniques apparentées) qui est plus efficace, car elle ne utilise que décalages et d'additions. Toutes ces méthodes sont couramment mis en oeuvre en matériel pour des raisons de performances.
Pour les calculs de très haute précision, lorsque la convergence de développement en série devient trop lente, les fonctions trigonométriques peuvent être estimés par le arithmétique moyenne géométrique, qui se rapproche de la fonction trigonométrique par le ( complexe ) intégrale elliptique.
Enfin, pour certains angles simples, les valeurs peuvent être calculées facilement à la main en utilisant le théorème de Pythagore , comme dans les exemples suivants. En fait, le sinus, cosinus et tangente de tout multiple entier de 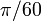 radians (3 °) peuvent être trouvés exactement à la main.
radians (3 °) peuvent être trouvés exactement à la main.
Considérons un triangle où les deux autres angles sont égaux, et sont donc à la fois 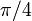 radians (45 °). Ensuite, la longueur du côté b et la longueur du côté a sont égaux; nous pouvons choisir
radians (45 °). Ensuite, la longueur du côté b et la longueur du côté a sont égaux; nous pouvons choisir 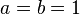 . Les valeurs de sinus, cosinus et tangente d'un angle de
. Les valeurs de sinus, cosinus et tangente d'un angle de 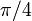 radians (45 °) peuvent alors être trouvés en utilisant le théorème de Pythagore:
radians (45 °) peuvent alors être trouvés en utilisant le théorème de Pythagore:
 .
.
Par conséquent:
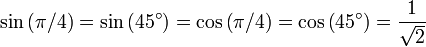 ,
, 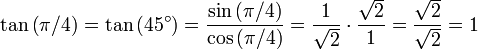 .
.
Pour déterminer les fonctions trigonométriques pour des angles de π / 3 radians (60 degrés) et π / 6 radians (30 degrés), nous commençons par un triangle équilatéral de la longueur du côté 1. Tous ses angles sont π / 3 radians (60 degrés). En le divisant en deux, on obtient un triangle rectangle avec π / 6 radians (30 degrés) et π / 3 radians (60 degrés) angles. Pour ce triangle, le côté le plus court = 1/2, le prochain grand côté = (√3) / 2 et l'hypoténuse = 1. Cela donne:
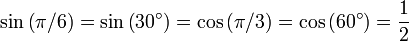 ,
, 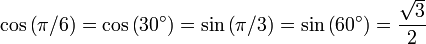 ,
, 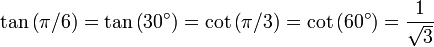 .
.
Fonctions inverses
Les fonctions trigonométriques sont périodiques, et donc pas injective, si strictement ils ne ont pas une fonction inverse . Par conséquent, pour définir une fonction inverse, nous devons restreindre leurs domaines de sorte que la fonction trigonométrique est bijective. Dans ce qui suit, les fonctions du côté gauche sont définies par l'équation de la droite; ce ne sont pas les identités prouvées. Les principaux inverses sont généralement définis comme:
Pour les fonctions trigonométriques inverses, les notations sin -1 et cos -1 sont souvent utilisés pour arcsin et arccos, etc. Lors de cette notation est utilisé, les fonctions inverses peuvent être confondus avec les inverses multiplicatifs des fonctions. La notation utilisant le préfixe "d'arc" évite une telle confusion, si "arcsec" peut être confondu avec " seconde d'arc ".
Tout comme le sinus et cosinus, les fonctions trigonométriques inverses peuvent également être définies en termes de série infinie. Par exemple,
Ces fonctions peuvent également être définis par prouvant qu'ils sont primitives d'autres fonctions. L'arc sinus, par exemple, peut se écrire comme l'intégrale suivante:
Des formules analogues pour les autres fonctions peuvent être trouvés à Fonction trigonométrique inverse. En utilisant le logarithme complexe, on peut généraliser toutes ces fonctions à des arguments complexes:
Propriétés et applications
Les fonctions trigonométriques, comme son nom l'indique, sont d'une importance cruciale dans la trigonométrie , principalement en raison des deux résultats suivants.
Loi des sinus
Le loi des sinus stipule que pour un arbitraire triangle de côtés a, b, et c et angles opposés les côtés A, B et C:
aussi connu comme:
où R est le rayon du triangle de circonscrit.

Il peut être prouvé en divisant le triangle en deux droits et l'utilisation de la définition ci-dessus sinusoïdale. La loi des sinus est utile pour calculer les longueurs des côtés d'un triangle inconnues si deux angles et un côté sont connus. Ce est une situation courante se passe dans triangulation, une technique pour déterminer les distances inconnues en mesurant deux angles et une distance clos accessible.
Loi des cosinus
Le loi des cosinus (aussi connu comme la formule du cosinus) est une extension du théorème de Pythagore :
aussi connu comme:
Dans cette formule, l'angle C est opposée à la face c. Ce théorème peut être prouvé en divisant le triangle en deux droits et en utilisant le théorème de Pythagore .
La loi des cosinus est surtout utilisé pour déterminer un côté d'un triangle si deux côtés et un angle sont connus, bien que dans certains cas, il peut y avoir deux solutions positives que dans le SSA cas ambigu. Et peut également être utilisé pour trouver le cosinus d'un angle (et par conséquent l'angle lui-même) si tous les côtés sont connus.
Autres propriétés utiles
Il existe également un la loi des tangentes:
Fonctions périodiques
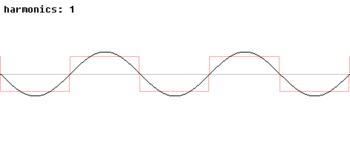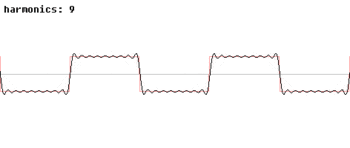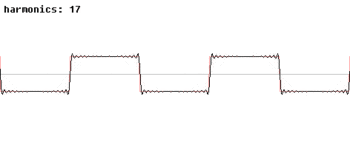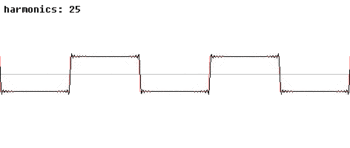
Les fonctions trigonométriques sont également importants dans la physique. Les fonctions sinus et cosinus, par exemple, sont utilisés pour décrire la mouvement harmonique simple, les modèles de nombreuses phénomènes naturels, tels que le mouvement d'une masse attachée à un ressort et, pour les petits angles, le mouvement pendulaire d'une pendaison collective par une chaîne. Les fonctions sinus et cosinus sont des projections unidimensionnelles de la le mouvement circulaire uniforme.
Les fonctions trigonométriques également se avérer utile dans l'étude des générale des fonctions périodiques. Ces fonctions ont des modèles d'onde caractéristiques que les graphiques, utiles pour la modélisation des phénomènes récurrents tels que sonores ou lumineux vagues . Chaque signal peut être écrit comme une (généralement infinie) somme de fonctions sinus et cosinus de différentes fréquences; ce est l'idée de base de L'analyse de Fourier, où des séries trigonométriques sont utilisés pour résoudre une variété de problèmes aux limites dans les équations aux dérivées partielles. Par exemple, le onde carrée, peut être écrit comme la série de Fourier
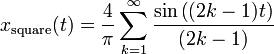 .
.
Dans l'animation sur la droite, on peut voir que quelques termes produisent déjà une assez bonne approximation.

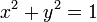
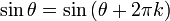
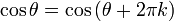
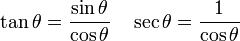
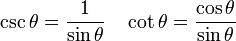
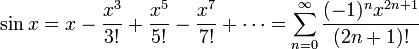
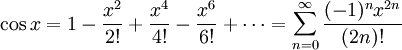
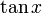
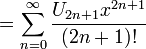
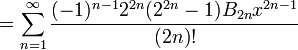

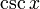
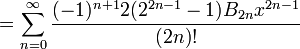

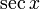
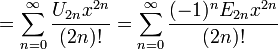

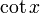
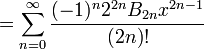

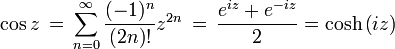
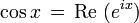
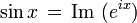
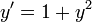
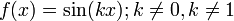
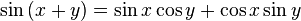
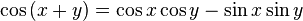
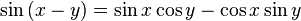
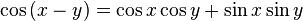
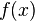
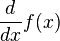
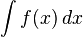
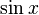
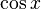
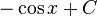
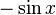
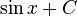
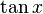
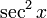
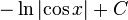
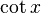
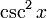
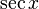
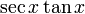
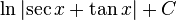
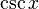
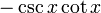
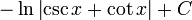
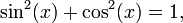
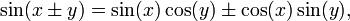
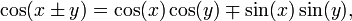

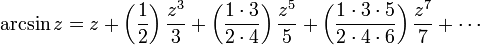

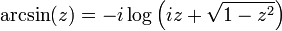
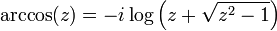
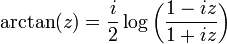
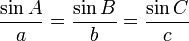
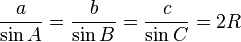
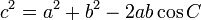
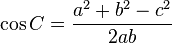
![\ Frac {a + b} {ab} = \ frac {\ tan [\ frac {1} {2} (A + B)]} {\ tan [\ frac {1} {2} (AB)]}](../../images/133/13346.png)
