Espace vectoriel

En mathématiques , un espace vectoriel (ou espace linéaire) est une collection d'objets (appelés vecteurs) que, de façon informelle, peut être mise à l'échelle et a ajouté. Plus formellement, un espace vectoriel est un ensemble sur lequel deux opérations, appelé (vecteur) et plus (scalaire) multiplication, sont définis et répondre à certaines naturelle axiomes qui sont énumérés ci-dessous. Espaces vectoriels sont les objets de base de l'étude de l'algèbre linéaire , et sont utilisés dans les mathématiques, les sciences et l'ingénierie.

Les espaces vectoriels les plus familiers sont deux et trois dimensions espaces euclidiens . Vecteurs dans ces espaces sont commandés paires ou triplets de nombres réels , et sont souvent représentés comme des vecteurs géométriques qui sont des quantités avec une amplitude et une direction, généralement représenté par des flèches. Ces vecteurs peuvent être ajoutés ensemble en utilisant la règle de parallélogramme ( d'addition de vecteurs ) ou multipliée par des nombres réels ( multiplication par un scalaire). Le comportement des vecteurs géométriques dans ces opérations constitue un bon modèle intuitif pour le comportement des vecteurs dans les espaces vectoriels plus abstraites, qui ne ont pas besoin d'une interprétation géométrique. Par exemple, l'ensemble des (vrais) polynômes forme un espace vectoriel.

Un espace vectoriel est une collection d'objets (appelés vecteurs) qui peuvent être mis à l'échelle et ajoutés.

Définition formelle

Soit F un champ (comme les nombres réels ou des nombres complexes ), dont éléments seront appelés scalaires. Un espace vectoriel sur le corps F est un ensemble V avec deux opérations binaires,

• addition vectorielle: V × V → V notée v + w, où v, w ∈ V, et
• multiplication scalaire: F × V → V dénotait un v, où a ∈ F et v ∈ V,

satisfaisant la axiomes ci-dessous. Quatre des axiomes exigent vecteurs de moins de plus pour former un groupe abélien, et deux sont lois de distribution.

1. plus de Vector est associative :

   Pour tout u, v, w ∈ V, on a u + (v + w) = (u + v) + w.

2. plus de Vector est commutatif :

   Pour tout v, w ∈ V, nous avons v + w = w + v.

3. plus de Vector a une élément de l'identité:

   Il existe un élément 0 ∈ V, appelé vecteur nul, tel que v + 0 = v pour tout v ∈ V.

4. plus de Vector a éléments inverses:

   Pour tout v ∈ V, il existe un élément w ∈ V, appelé Opposé de v, tel que v + w = 0.

5. Distributivity détient pour la multiplication scalaire sur l'addition de vecteur:

   Pour tout a ∈ F et v, w ∈ V, nous avons un (v + w) = a v + a w.

6. Distributivity détient pour la multiplication scalaire sur l'addition de champ:

   Pour tout a, b ∈ F et v ∈ V, nous avons (a + b) v = a + b v v.

7. Multiplication scalaire est compatible avec la multiplication dans le domaine des scalaires:

   Pour tout a, b ∈ F et v ∈ V, nous avons un (v b) = (ab) c.

8. Multiplication scalaire a une élément de l'identité:

   Pour tout v ∈ V, nous avons une v = v, où 1 représente le identité multiplicatif dans F.

Formellement, ce sont les axiomes pour une module, un espace vectoriel peut être concise décrit comme un module sur un champ.

Notez que le septième axiome ci-dessus, indiquant un (v b) = (ab) v, ne est pas affirmer l' associativité d'une opération, car il ya deux opérations en question, multiplication scalaire: b v; et sur le terrain multiplication: ab.

Certaines sources choisissent d'inclure également deux axiomes de fermeture:

1. V est fermé en vertu de l'addition de vecteurs:

   Si u, v ∈ V, alors u + v ∈ V.

2. V est fermé en vertu de multiplication scalaire:

   Si a ∈ F, v ∈ V, puis un v ∈ V.

Cependant, la compréhension formelle moderne des opérations que des cartes avec codomain V implique ces déclarations, par définition, et évite ainsi le besoin de les énumérer comme des axiomes indépendants. La validité des axiomes de fermeture est essentielle pour déterminer si un sous-ensemble d'un espace vectoriel est un sous-espace.

Notez que les expressions de la forme "v un", où v ∈ V et a ∈ F, sont, à proprement parler, pas définies. En raison de la commutativité du champ sous-jacente, cependant, "a v" et "v a" sont souvent traités comme des synonymes. En outre, si v ∈ V, w ∈ V, et un ∈ F où l'espace vectoriel V est en outre une algèbre sur le champ F alors une v w = v a w, qui le rend pratique à considérer «une v" et "v a" pour représenter le même vecteur.

Propriétés élémentaires

Il ya un certain nombre de propriétés qui suivent facilement des axiomes de l'espace vectoriel.

• Le vecteur nul 0 ∈ V est unique:

  Si 0 ₁ et 0 ₂ sont des vecteurs nuls en V, tel que 0 + ₁ v = 0 et ₂ + v = v pour tout v ∈ V, puis 0 ₁ 0 ₂ = = 0.

• Multiplication scalaire avec le vecteur nul donne le vecteur nul:

  Pour tout a ∈ F, nous avons un 0 = 0.

• Scalar multiplication par zéro donne le vecteur nul:

  Pour tout v ∈ V, nous avons 0 v = 0, où 0 représente l'identité additif dans F.

• Aucune autre multiplication scalaire donne le vecteur nul:

  Nous avons v = 0 si et seulement si a = 0 ou c = 0.

• L'inverse additif - v d'un vecteur v est unique:

  Si w ₁ et w ₂ sont les inverses des additifs v ∈ V, tel que v + w ₁ = 0 et v + w ₂ = 0, alors w = ₁ w _2. Nous appelons l'inverse - v et w définissons - v ≡ w + (- v).

• Multiplication scalaire par unité négative donne l'inverse additif du vecteur:

  Pour tout v ∈ V, on a (-1) v = - v, où 1 désigne l'identité multiplicative en C.

• Négation commute librement:

  Pour tout a ∈ F et v ∈ V, nous avons (- a) v = a (- v) = - (V).

Exemples

Sous-espaces et des bases

Principaux articles: Sous-espace vectoriel, Base

Étant donné un espace vectoriel V, un non vide sous-ensemble W de V qui est fermé par addition et multiplication par un scalaire est appelé sous-espace de V. sous-espaces de V sont des espaces vectoriels (plus le même domaine) dans leur propre droit. L'intersection de tous les sous-espaces formés d'un ensemble donné de vecteurs est appelé son durée; si aucun vecteur peut être enlevé sans changer la durée, l'ensemble est dit linéairement indépendantes. Un ensemble linéairement indépendant dont la durée est V est appelé base de V.

Utilisation Lemme de Zorn (ce qui équivaut à la axiome du choix), il peut être prouvé que chaque espace vectoriel a une base. Il résulte de ce ultrafiltre lemme, qui est plus faible que l'axiome du choix, que toutes les bases d'un espace vectoriel donné ont la même cardinalité. Ainsi espaces vectoriels sur un domaine donné sont fixés jusqu'à isomorphisme par un seul nombre cardinal (appelé dimension de l'espace vectoriel) représentant la taille de la base. Par exemple, les espaces réels vecteurs de dimension finie ne sont que R ^0, R ^1, R ^2, R ^3, .... La dimension de l'espace vectoriel réel R ³ est de trois.

Il était séparé F. qui, le premier prouvé que tout espace vectoriel a une base. Andreas Blass a montré ce théorème conduit à la axiome du choix.

Une base permet d'exprimer tout vecteur de l'espace comme un tuple unique des éléments sur le terrain, bien que la prudence doit être exercée quand un espace vectoriel n'a pas de base finie. Espaces vectoriels sont parfois introduits à partir de ce point de vue coordinatised.

On considère souvent les espaces vectoriels qui portent également compatible topologie. Compatible signifie ici que l'addition et la multiplication scalaire devraient être des opérations continues. Cette condition assure en fait que la topologie donne lieu à une structure uniforme. Lorsque la dimension est infinie, il ya généralement plus d'une topologie de inéquivalentes, ce qui rend l'étude des espaces vectoriels topologiques plus riche que celle des espaces vectoriels générales.

Seulement en tel espaces vectoriels topologiques peut-on considérer les sommes infinies de vecteurs, ce est- série, à travers la notion de convergence. Ceci est d'une importance dans les deux mathématiques race pure et appliquée, par exemple en mécanique quantique , où les systèmes physiques sont définies comme Espaces de Hilbert, ou lorsque expansions de Fourier sont utilisés.

Cartes linéaires

Article détaillé: Linéaire

Compte tenu de deux espaces vectoriels V et W sur le même champ F, on peut définir cartes linéaires ou «transformations linéaires" de V dans W. Ce sont des fonctions f: V → W qui sont compatibles avec la structure pertinente - ce est à dire, ils conservent sommes et produits scalaires. L'ensemble de toutes les cartes linéaires de V à W, noté Hom _F (V, W), est aussi un espace vectoriel sur F. Lorsque bases à la fois V et W sont donnés, cartes linéaires peuvent être exprimées en termes de composants comme matrices .

Une isomorphisme est linéaire carte 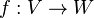de sorte qu'il existe un plan inverse 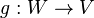tel que 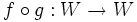et sont cartes d'identité. Une carte linéaire qui est à la fois une à une ( injective) et sur ( surjective) est nécessairement un isomorphisme. Se il existe un isomorphisme entre V et W, les deux espaces sont dits isomorphes; ils sont alors essentiellement identique à celle des espaces vectoriels.

Les espaces vectoriels sur un corps fixe F ainsi que les cartes linéaires sont un catégorie, en effet une catégorie abélienne.

Généralisations

D'un point de vue abstrait, espaces vectoriels sont modules sur un champ, F. La pratique courante de l'identification d'un V et V a dans un espace vectoriel rend l'espace vectoriel un F - F bimodule. Modules dans le besoin général de ne pas avoir des bases; ceux qui le font (y compris tous les espaces vectoriels) sont connus comme modules libres.

Une famille d'espaces vectoriels, paramétré en permanence par certains sous-jacente espace topologique, est un fibré.

Une espace affine est un ensemble avec un action transitive d'espace vectoriel. Notez qu'un espace vectoriel est un espace affine sur elle-même, par le carte de structure

Structures supplémentaires

Il est commun pour étudier les espaces vectoriels avec certaines structures supplémentaires. Ce est souvent nécessaire pour récupérer notions ordinaires de la géométrie.

• Un espace réel ou complexe vecteur avec un concept bien défini de longueur, soit un norme, est appelé un espace vectoriel normé.
• Un espace vectoriel normé avec le concept plus bien définie de l'angle est appelé espace intérieur du produit.
• Un espace vectoriel avec un topologie compatible avec les opérations - de telle sorte que l'addition et la multiplication par un scalaire sont cartes continues - est appelé espace vectoriel topologique. La structure topologique est pertinente lorsque l'espace vectoriel sous-jacent est de dimension infinie.

• Un espace vectoriel avec un supplément opérateur bilinéaire définissant la multiplication des deux vecteurs est un algèbre sur un champ.
• Une espace vectoriel ordonné.