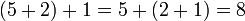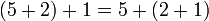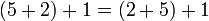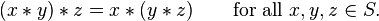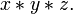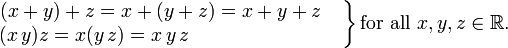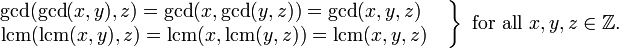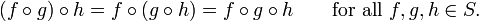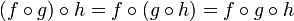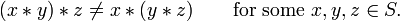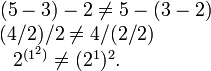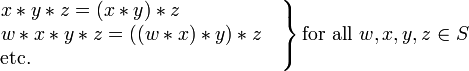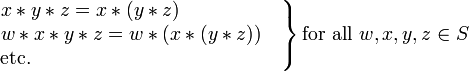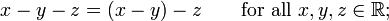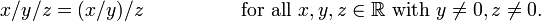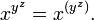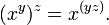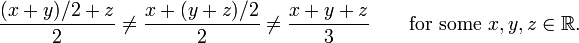Associatividade

Assuntos Relacionados: Matemática

Você sabia ...

Esta seleção é feita para as escolas de caridade infantil leia mais . Com SOS Children você pode escolher para patrocinar crianças em mais de cem países

Em matemática , a associatividade é uma propriedade que um operação binária pode ter. Isso significa que, dentro de uma expressão contendo dois ou mais dos mesmos operadores associativos em uma fileira, a ordem das operações não tem importância, contanto que a sequência do operandos não é alterado. Ou seja, reorganizando a parênteses em uma expressão como essa não vai mudar seu valor. Considere, por exemplo, a equação

$(5 + 2) + 1 = 5 + (2 + 1) = 8$

Mesmo que os parênteses foram rearranjadas, o valor da expressão não foi alterada. Uma vez que este é verdadeiro quando se realiza além de quaisquer números reais , dizemos que "além de números reais é uma operação associativa."

Associatividade não é para ser confundido com comutatividade . Comutatividade justifica alterar a ordem ou seqüência dos operandos dentro de uma expressão enquanto associatividade não. Por exemplo,

$(5 + 2) + 1 = 5 + (2 + 1)$

é um exemplo de associamento porque os parênteses foram alteradas (e, consequentemente, a ordem das operações durante a avaliação), enquanto que os operandos 5, 2 e 1 apareceu na mesma ordem da esquerda para a direita na expressão.

$(5 + 2) + 1 = (2 + 5) 1$

não é um exemplo de associamento porque a sequência alterada quando operando a 2 e 5 comutada lugares.

Operações associativas são abundantes em matemática, e na verdade a maioria estruturas algébricas explicitamente exigem suas operações binárias para ser associativo. No entanto, muitas operações importantes e interessantes são não-associativa; Um exemplo comum seria o produto do vetor cruz .

Definição

Formalmente, uma operação binária 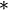$* \! \! \!$ em um definir S é chamado associativo se ele satisfaz a lei associativa:

$(X * y) * z = x * (y * z) \ qquad \ mbox {para todo} x, y, z \ in S.$

A ordem de avaliação não afeta o valor de tais expressões, e se puder ser demonstrado que o mesmo vale para expressões contendo qualquer número de 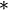$* \! \! \!$ operações. Assim, quando 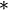$* \! \! \!$ é associativa, a ordem de avaliação pode, portanto, ser deixado sem especificação sem causar ambiguidade, ao omitir os parênteses e escrevendo simplesmente:

$x * y * z. \,$

No entanto, é importante lembrar que a alteração da ordem das operações não envolve ou permitem mudar as próprias operações reais movendo os operandos em torno dentro da expressão.

Exemplos

Alguns exemplos de operações associativos incluem o seguinte.

Em aritmética , adição e multiplicação de números reais são associativas; isto é,

$\ Esquerda. \ Begin {matriz} (x + y) + z = x + (Y + Z) = x + y + z \ quad \\ (x \, y) = z x (y \, z) = x \, Y \ , z \ qquad \ qquad \ qquad \ quad \ \ \, \ end {matrix} \ right \} \ mbox {para todo} x, y, z \ in \ mathbb {R}.$

Adição e multiplicação de números complexos e quaternions é associativa. A adição de octoniões também é associativa, mas multiplicação de octoniões é não associativa.

O máximo divisor comum e múltiplas funções menos comuns agir de forma associativa.

$\ Esquerda. \ Begin {matrix} \ operatorname {} mdc (\ operatorname {} mdc (x, y), z) = \ operatorname {} mdc (x, \ operatorname {} mdc (y, z)) = \ operatorname {} mdc (x, y, z) \ \ quad \\ \ operatorname {} LCM (\ operatorname {} LCM (x, y), z) = \ operatorname {} LCM (x, \ operatorname {} LCM (y, z) ) = \ operatorname {} lcm (x, y, z) \ quad \ end {matrix} \ right \} \ mbox {para todo} x, y, z \ in \ mathbb {Z}.$

Porque transformações lineares são funções que podem ser representados por matrizes com a multiplicação de matrizes ser a representação de composição funcional, pode-se concluir de imediato que a multiplicação de matrizes é associativa.

Tomando a intersecção ou o união de conjuntos:

$\ Esquerda. \ Begin {matrix} (A \ cap B) \ cap C = A \ cap (B \ cap C) = A \ cap B \ cap C \ quad \\ (A \ cup B) \ cup C = A \ copo ( B \ cup C) = A \ cup B \ cup C \ quad \ end {matrix} \ right \} \ mbox {} para todos os conjuntos A, B, C.$

Se M é um conjunto e S denota o conjunto de todas as funções de M a M, então a operação de composição funcional em S é associativa:

$(F \ circ g) \ circ h = f \ circ (g \ circ h) = f \ circ g \ circ h \ qquad \ mbox {para todo} f, g, h \ in S.$

Ligeiramente mais geralmente, dada quatro conjuntos de M, N, P e Q, com h: M para N, G: N a P, e f: P a Q, então

$(F \ circ g) \ circ h = f \ circ (g \ circ h) = f \ circ g \ circ h$

como antes. Em suma, a composição de mapas é sempre associativa.

Considere um conjunto com três elementos, A, B, e C. A seguinte operação:

×	A	B	C
+
A	A	A	A
B	A	B	C
C	A	A	A

é associativa. Assim, por exemplo, A (BC) = (AB) C. Este mapeamento não é comutativa.

Não associatividade

A operação binária 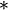$*$ em um conjunto S que não satisfaz a lei associativa é chamado de não-associativa. Simbolicamente,

$(X * y) * z \ ne x * (y * z) \ qquad \ mbox {} para algum x, y, z \ in S.$

Para tal operação a ordem de avaliação não importa. subtração , divisão e exponenciação são exemplos bem conhecidos de operações não-associativas:

$\ Begin {matrix} (5-3) -2 \ ne 5- (3-2) \ quad \\ (4/2) / 2 \ ne 4 / (2/2) \ qquad \ \\ qquad 2 ^ { (1 ^ 2)} \ ne (2 ^ 1) ^ 2. \ quad \ qquad \ qquad \ end {matrix}$

Em geral, deve ser parênteses usados para indicar o ordem de avaliação, se uma operação de não-associativa aparece mais de uma vez em uma expressão. No entanto, os matemáticos concordam com uma determinada ordem de avaliação para várias operações não-associativas comuns. Isto é simplesmente uma convenção sintática para evitar parênteses.

Uma operação de esquerda-associativa é uma operação não-associativa que é convencionalmente avaliadas da esquerda para a direita, ou seja,

$\ Esquerda. \ Begin {matrix} x * y * z = (x * y) * z \ qquad \ qquad \ quad \, \\ w * x * y * z = ((w * x) * y) * z \ quad \ \ \ mbox {etc.} \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad \ \ \, \ end {matrix} \ right \} \ mbox {para todo} w, x, y, z \ in S$

enquanto uma operação de direito associativo é convencionalmente avaliadas da direita para a esquerda:

$\ Esquerda. \ Begin {matrix} x * y * z = x * (y * z) \ qquad \ qquad \ quad \, \\ w * x * y * z = w * (x * (y * z)) \ quad \ \ \ mbox {etc.} \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad \ \ \, \ end {matrix} \ right \} \ mbox {para todo} w, x, y, z \ in S$

Ambas as operações associativa à esquerda e à direita-associativas ocorrer; exemplos são dados abaixo.

Mais exemplos

Operações associativa à esquerda incluem o seguinte.

Subtração e divisão de números reais:

$xyz = (xy) -z \ qquad \ mbox {para todo} x, y, z \ in \ mathbb {R};$

$x / y / z = (x / y) / z \ qquad \ qquad \ quad \ mbox {para todo} x, y, z \ in \ mathbb {R} \ mbox {com} y \ ne0, z \ ne0.$

Operações direito do associativos incluem o seguinte.

Exponenciação de números reais:

$x ^ {y ^ z} = x ^ {(y ^ z)}. \,$

A razão exponenciação é associativa à direita é que uma operação repetida exponenciação esquerda associativa seria menos útil. Várias aparições poderia (e iria) ser reescrita com a multiplicação:

$(X ^ y) ^ z = x ^ {(yz)}. \,$

Operações não-associativos para que nenhuma ordem de avaliação convencional é definido incluem o seguinte.

Tomando o pairwise média de números reais:

${(X + y) / 2 + z \ over2} \ ne {x + (y + z) / 2 \ over2} \ ne {x + y + z \ over3} \ qquad \ mbox {por algum} X, Y, z \ in \ mathbb {R}.$

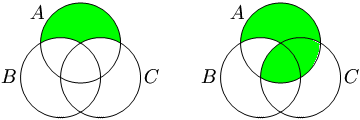
Tomando o complemento relativo dos conjuntos de:

$(A \ barra invertida B) \ barra invertida C \ ne A \ barra invertida (B \ barra invertida C) \ qquad \ mbox {} para alguns conjuntos A, B, C.$

$Diagrama de Venn dos complementos relativos (A \ B) \ C e A \ (B \ C)$

A parte verde na esquerda diagrama de Venn representa (A \ B) \ C. A parte verde no diagrama de Venn direita representa A \ (B \ C).

Usando a notação direito associativo para condicional material pode ser motivada por exemplo, Curry-Howard correspondência: ver, por exemplo comparação dos dois primeiros axiomas do sistema dedução Hilbert-estilo com combinadores básicos da lógica combinatória.

Retirado de " http://en.wikipedia.org/w/index.php?title=Associative_property&oldid=202029355 "