
Carl Friedrich Gauss
Informações de fundo
Crianças SOS, que corre cerca de 200 sos escolas no mundo em desenvolvimento, organizado esta selecção. SOS mães cada um cuidar de uma família de crianças apadrinhadas .
| Carl Friedrich Gauss | |
|---|---|
 Carl Friedrich Gauss (1777-1855), pintado por Christian Albrecht Jensen | |
| Nascido | 30 de abril de 1777 Braunschweig, Ducado de Brunswick-Wolfenbüttel, Sacro Império Romano |
| Morreu | 23 de fevereiro de 1855 (77 anos) Göttingen, Reino de Hanover |
| Residência | Reino de Hanover |
| Nacionalidade | Alemão |
| Campos | Matemática e física |
| Instituições | Universidade de Göttingen |
| Alma mater | Universidade de Helmstedt |
| Conselheiro doutoral | Johann Friedrich Pfaff |
| Outros assessores acadêmicos | Johann Christian Martin Bartels |
| Os estudantes de doutorado | Friedrich Bessel Christoph Gudermann Christian Ludwig Gerling Richard Dedekind Johann Encke Johann Listing Bernhard Riemann Christian Peters Moritz Cantor |
| Outros alunos notáveis | Johann Dirichlet Gotthold Eisenstein Carl Wolfgang Benjamin Goldschmidt Gustav Kirchhoff Ernst Kummer August Ferdinand Möbius LC Schnürlein Julius Weisbach |
| Conhecido por | Veja a lista completa |
| Influenciado | Sophie Germain |
| Prêmios Notáveis | Medalha Copley (1838) |
Assinatura  | |
Johann Carl Friedrich Gauss (pron .: / ɡ aʊ s /; alemão : Gauß, pronunciado [Ɡaʊs]; latim : Carolus Fridericus Gauss) (30 de abril de 1777 - 23 de fevereiro de 1855) foi um Alemão matemático e cientista físico que contribuíram de forma significativa para muitos campos, incluindo a teoria dos números , álgebra , estatísticas , análise , geometria diferencial , geodésia, geofísica, eletrostática, astronomia e ótica .
Às vezes referido como o mathematicorum Princeps ( Latina , "o Príncipe de Matemáticos" ou "o principal dos matemáticos") e "maior matemático desde a antiguidade", Gauss teve uma influência notável em muitos campos da matemática e da ciência e é classificado como um dos matemáticos mais influentes da história. Ele se referiu à matemática como "a rainha das ciências".
Primeiros anos (1777-1798)

Carl Friedrich Gauss nasceu em 30 de abril de 1777 em Braunschweig (Brunswick), na Ducado de Braunschweig-Wolfenbüttel, agora parte da Baixa Saxónia, Alemanha , como o filho de pais da classe trabalhadora pobres. Na verdade, sua mãe era analfabeta e nunca gravada a data de seu nascimento, lembrando apenas que ele havia nascido em uma quarta-feira, oito dias antes da Festa da Ascensão, que por si só ocorre 40 dias após a Páscoa . Gauss viria a resolver este enigma sobre a sua data de nascimento no contexto da encontrando a data da Páscoa, derivando métodos para calcular a data em ambos os anos passados e futuros. Ele foi batizado e confirmou em uma igreja perto da escola ele frequentou quando criança.
Gauss foi um criança prodígio. Há muitas anedotas sobre sua precocidade, enquanto uma criança, e ele fez suas primeiras descobertas matemáticas inovadoras quando ainda era adolescente. Ele completou Disquisitiones Arithmeticae, sua opus magnum, em 1798 com a idade de 21, embora não foi publicado até 1801. Este trabalho foi fundamental na consolidação da teoria dos números como uma disciplina e moldou o campo até os dias atuais.
Habilidades intelectuais de Gauss atraiu a atenção do Duque de Braunschweig, que o mandou para o Collegium Carolinum (agora Technische Universität Braunschweig), o qual ele participou de 1792-1795, e ao Universidade de Göttingen de 1795 a 1798. Enquanto estava na universidade, Gauss redescoberto independentemente diversos teoremas importantes; a sua descoberta em 1796 ocorreu quando ele mostrou que qualquer regulares polígono com um certo número de lados que é um Fermat prime (e, por conseguinte, esses polígonos com qualquer número de lados que é o produto de números primos de Fermat distintos e uma potência de 2) pode ser construído por régua e compasso . Esta foi uma grande descoberta em um importante campo de matemática; problemas de construção tinham ocupado os matemáticos desde os dias dos gregos antigos , ea descoberta levou Gauss para escolher em vez de matemática filologia como uma carreira. Gauss ficou tão satisfeito com este resultado que ele pediu que um regular heptadecagon ser inscrito em sua lápide. O pedreiro recusou, afirmando que a construção difícil seria, essencialmente parecido com um círculo.
O ano de 1796 foi o mais produtivo para ambos Gauss e teoria dos números. Descobriu uma construção do heptadecagon em 30 de Março. Avançou ainda aritmética modular , simplificando enormemente manipulações na teoria dos números. Em 8 de abril, ele se tornou o primeiro a provar a lei da reciprocidade quadrática. Esta lei extremamente geral permite matemáticos para determinar a solvabilidade de qualquer equação quadrática na aritmética modular. O teorema de número primo, conjecturou em 31 de Maio, dá uma boa compreensão de como os números primos são distribuídos entre os números inteiros. Gauss também descobriu que todo inteiro positivo é representável como uma soma de no máximo três números triangulares em 10 de julho e, em seguida, anotou em seu diário a famosa nota: " ΕΥΡΗΚΑ! num = Δ + Δ + Δ ". Em 1º de outubro, ele publicou um resultado sobre o número de soluções de polinômios com coeficientes em campos de finitos, que 150 anos depois levaram à Conjecturas de Weil.
Anos médios (1799-1830)
Em seu doutorado em 1799 revelia, uma nova prova do teorema de que cada função algébrica racional integrante de uma variável pode ser resolvido em fatores reais de primeiro ou segundo grau, Gauss provou a teorema fundamental da álgebra que estabelece que todo de uma variável não constante polinômio com coeficientes complexos tem pelo menos um complexo root. Os matemáticos incluindo Jean le Rond d'Alembert havia produzido provas falsas antes dele, e dissertação de Gauss contém uma crítica da obra de d'Alembert. Ironicamente, ao padrão de hoje, própria tentativa de Gauss não é aceitável, devido ao uso implícito do Jordan curva teorema. No entanto, ele posteriormente produziu três outras provas, a última em 1849, sendo geralmente rigorosa. Suas tentativas clarificado o conceito de números complexos consideravelmente ao longo do caminho.
Gauss também fez importantes contribuições à teoria dos números com o seu livro de 1801 Disquisitiones Arithmeticae ( Latina , aritméticos Investigações), que, entre coisas, introduziu o símbolo ≡ para congruência e é usado em uma apresentação limpa de aritmética modular , continha as duas primeiras provas da lei de reciprocidade quadrática, desenvolveu as teorias de binários e ternários formas quadráticas, afirmou o classe problema número para eles, e mostrou que um regular heptadecagon (polígono de 17 lados) pode ser construído com esquadro e compasso .

Nesse mesmo ano, italiano astrônomo Giuseppe Piazzi descobriu o planeta anão Ceres . Piazzi só podia controlar Ceres durante alguns meses, seguindo-o por três graus em todo o céu noturno. Em seguida, ele desapareceu temporariamente por trás do brilho do Sol Vários meses depois, quando Ceres deveria ter reaparecido, Piazzi não podia localizá-lo: as ferramentas matemáticas da época não foram capazes de extrapolar uma posição a partir de uma quantidade tão escassa de dados em três graus representam menos de 1% da órbita total.
Gauss, que tinha 23 anos na época, ouviu falar sobre o problema e abordou-lo. Depois de três meses de trabalho intenso, ele previu uma posição para Ceres em dezembro 1801-apenas cerca de um ano após a sua primeira aparição, e isto acabou por ser precisos dentro de uma meia-grau, quando foi redescoberto por Franz Xaver von Zach no dia 31 de dezembro no Gota, e um dia mais tarde por Heinrich Olbers em Bremen.
O método de Gauss envolveu a determinação de uma seção cônica no espaço, dado um foco (o Sol) e intersecção do cônica com três linhas de dados (linhas de visão da Terra, que é movendo-se em uma elipse, para o planeta) e dado o tempo que converte o planeta para atravessar os arcos determinadas por estas linhas (a partir do qual os comprimentos dos arcos pode ser calculado pela segunda lei de Kepler). Este problema leva a uma equação do oitavo grau, do que uma solução, a órbita da terra, é conhecida. A solução requerida é, em seguida, separada do restante seis com base nas condições físicas. Neste trabalho Gauss usou métodos de aproximação abrangentes que ele criou para o efeito.
Um desses métodos era a Transformada de Fourier rápido. Enquanto este método é que tradicionalmente se atribui a um artigo de 1965 por JW Cooley e JW Tukey, Gauss desenvolveu-lo como um método de interpolação trigonométrica. Seu papel, Theoria Interpolationis Methodo Nova Tractata, só foi publicado postumamente em Volume 3 de suas obras completas. Este documento é anterior à primeira apresentação por Joseph Fourier sobre o assunto em 1807.
Zach observou que "sem o trabalho inteligente e cálculos de Doutor Gauss nós não poderia ter encontrado Ceres novamente". Embora Gauss tinha até esse ponto foi apoiado financeiramente pelo seu estipêndio do Duque, ele duvidou da segurança desse arranjo, e também não acreditava matemática pura para ser suficientemente importante para merecer apoio. Assim, ele buscou uma posição em astronomia, e em 1807 foi nomeado professor de Astronomia e diretor do astronômica observatório em Göttingen, cargo que ocupou durante o resto de sua vida.
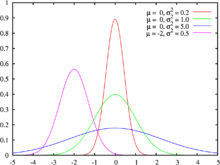
A descoberta de Ceres levou Gauss ao seu trabalho sobre a teoria do movimento de planetóides perturbado por grandes planetas, eventualmente, publicados em 1809 como Theoria motus corporum coelestium em sectionibus conicis solem ambientum (Teoria de movimento dos corpos celestes em movimento em seções cônicas em todo o Sun). No processo, ele então racionalizado a matemática complicados de previsão orbital do século 18 que o seu trabalho continua a ser uma pedra angular da computação astronômico. Ele introduziu o Constante gravitacional de Gauss, e continha um tratamento influente do método dos mínimos quadrados , um procedimento utilizado em todas as ciências até hoje, para minimizar o impacto de erro de medição. Gauss provou o método sob o pressuposto de distribuição normal de erros (ver Gauss-Markov teorema; Veja também Gaussiana). O método tinha sido descrito antes por Adrien-Marie Legendre em 1805, mas Gauss alegou que tinha sido usado desde 1795.

Em 1818 Gauss, colocando suas habilidades de cálculo para o uso prático, levou a cabo uma levantamento geodésico do Reino de Hanover, ligando-se com anteriores dinamarqueses inquéritos. Para ajudar a pesquisa, Gauss inventou o heliotrópio, um instrumento que utiliza um espelho para refletir a luz solar através de grandes distâncias, para medir posições.
Gauss também alegou ter descoberto a possibilidade de geometrias não-euclidiana, mas nunca publicou. Esta descoberta foi uma grande mudança de paradigma em matemática, uma vez que libertou os matemáticos a partir da crença equivocada de que axiomas de Euclides foram a única maneira de fazer geometria consistente e não-contraditórias. A investigação sobre estas geometrias levou, entre outras coisas, Einstein teoria da relatividade geral, que descreve o universo como não-euclidiana 's. Seu amigo Farkas Wolfgang Bolyai com quem Gauss tinha jurado "fraternidade ea bandeira da verdade" como um estudante, havia tentado em vão durante muitos anos para provar o postulado paralelo a partir de outros axiomas de Euclides da geometria. O filho de Bolyai, János Bolyai, descobriu geometria não-euclidiana, em 1829; seu trabalho foi publicado em 1832. Depois de ver isso, Gauss escreveu para Farkas Bolyai: "Para elogiá-lo equivaleria a elogiar-me por todo o conteúdo do trabalho ... coincide quase exatamente com as minhas próprias meditações que ocuparam minha mente para. Nos últimos trinta ou trinta e cinco anos. "
Esta afirmação não comprovada colocar uma pressão sobre seu relacionamento com János Bolyai (que pensavam que Gauss foi "roubar" a sua ideia), mas agora é geralmente feita pelo valor de face. Cartas de Gauss anos antes de 1829 revelar obscuramente discutir o problema de linhas paralelas. Waldo Dunnington, um biógrafo de Gauss, argumenta em Gauss, Titan of Science que Gauss foi, de facto, em plena posse de geometria não-euclidiana muito antes de ser publicado pela János Bolyai, mas que ele se recusou a publicar algum dele por causa de seu medo de controvérsia.
A pesquisa de Hanover despertado interesse de Gauss em geometria diferencial , um campo da matemática que lidam com curvas e superfícies. Entre outras coisas ele veio com a noção de Curvatura Gaussian. Isso levou em 1828 a um teorema importante, o Theorema Egregium (notável teorema), que cria uma propriedade importante da noção de curvatura. Informalmente, o teorema diz que a curvatura de uma superfície pode ser determinada inteiramente pela medição ângulos e distâncias na superfície. Isto é, a curvatura não depende de como a superfície pode ser incorporado no espaço 3-dimensional ou espaço 2-dimensional.
Em 1821, foi feito a um membro estrangeiro da Real Academia Sueca de Ciências.
Anos mais tarde e morte (1831-1855)

Em 1831 Gauss desenvolveu uma frutífera colaboração com o professor de física Wilhelm Weber, levando a novos conhecimentos em magnetismo (incluindo a determinação de uma representação para a unidade de magnetismo em termos de massa, comprimento e hora) e a descoberta de Leis de Kirchhoff em eletricidade. Foi durante este período que ele formulou o seu homónimo lei . Eles construíram o primeiro telégrafo eletromecânico em 1833, que ligava o observatório com o instituto de física em Göttingen. Gauss pedi um magnético observatório a ser construído no jardim do observatório, e com Weber fundou a "Magnetischer Verein" (clube magnética em alemão ), que apoiou medidas do campo magnético da Terra em muitas regiões do mundo. Ele desenvolvido um método de medição da intensidade horizontal do campo magnético que estava a ser utilizado bem na segunda metade do século 20, e elaboraram a teoria matemática para separar o interior e exterior ( magnetospheric) fontes de campo magnético da Terra.
Em 1840, Gauss publicou seu influente Dioptrische Untersuchungen, na qual ele deu a primeira análise sistemática sobre a formação de imagens sob uma aproximação paraxial ( Óptica Gauss). Entre os seus resultados, Gauss mostrou que, sob uma aproximação paraxial um sistema óptico pode ser caracterizada pela sua pontos cardeais e ele derivou a fórmula lente de Gauss.
Em 1854, Gauss nomeadamente selecionou o tema para Bernhard Riemann 's agora famoso Habilitationvortrag, Über welche der Geometrie zu Grunde liegen morrer Hypothesen,. No caminho para casa de conferência de Riemann, Weber relatou que Gauss estava cheio de elogios e entusiasmo.
Gauss morreu em Göttingen, na Reino de Hannover (agora parte da Baixa Saxónia, Alemanha) em 1855 e está enterrado no Albani-Friedhof cemitério lá. Dois indivíduos deram elogios em seu funeral: Gauss do filho-de-lei Heinrich Ewald e Wolfgang von Sartorius Waltershausen, que era amigo íntimo e biógrafo de Gauss. Seu cérebro foi preservado e foi estudado por Rudolf Wagner que encontrou a sua massa de 1492 gramas e ser a área cerebral igual a 219.588 milímetros quadrados (340,362 polegadas quadradas). Circunvoluções altamente desenvolvidos também foram encontrados, que no início do século 20 foi sugerida como a explicação de seu gênio.
Religião
Bühler escreve que, de acordo com a correspondência com Rudolf Wagner, Gauss não pareceu acreditar em um deus pessoal. Ele foi dito ser um deísta. Ele afirma ainda que, apesar de Gauss firmemente acreditava na imortalidade da alma e em algum tipo de vida após a morte, não foi de uma forma que poderia ser interpretado como cristão.
De acordo com Dunnington, religião de Gauss foi baseada na busca da verdade. Ele acreditava na "imortalidade da individualidade espiritual, em uma permanência pessoal depois da morte, em uma última ordem das coisas, em um Deus eterno, justo, onisciente e onipotente". Gauss também confirmada tolerância religiosa, acreditando que é errado incomodar os outros que estavam em paz com suas próprias crenças.
Família

A vida pessoal de Gauss foi ofuscada pela morte precoce de sua primeira esposa, Johanna Osthoff, em 1809, logo seguido pela morte de um filho, Louis. Gauss mergulhou em uma depressão a partir do qual nunca se recuperou totalmente. Ele casou-se novamente, a melhor amiga de Johanna chamado Friederica Wilhelmine Waldeck mas comumente conhecido como Minna. Quando sua segunda esposa morreu em 1831 após uma longa doença, uma de suas filhas, Therese, assumiu o lar e cuidados Gauss até o fim de sua vida. Sua mãe viveu em sua casa de 1817 até sua morte em 1839.
Gauss teve seis filhos. Com Johanna (1780-1809), seus filhos eram Joseph (1806-1873), Wilhelmina (1808-1846) e Louis (1809-1810). De todos os filhos de Gauss, Wilhelmina foi dito ter vindo mais próximo de seu talento, mas ela morreu jovem. Com Minna Waldeck ele também teve três filhos: Eugene (1811-1896), Wilhelm (1813-1879) e Therese (1816-1864). Eugene compartilhado uma boa medida do talento de Gauss em idiomas e computação. Therese cuidava da casa para Gauss até sua morte, depois que ela se casou.
Gauss, eventualmente, teve conflitos com seus filhos. Ele não queria que algum de seus filhos para entrar matemática ou ciência para "medo de abaixar o nome da família". Gauss queria Eugene para se tornar um advogado, mas Eugene queria estudar línguas. Eles tiveram uma discussão sobre uma festa realizada Eugene, que Gauss se recusou a pagar. O filho deixou com raiva e, em cerca de 1832, emigrou para os Estados Unidos, onde foi muito bem sucedida. Wilhelm também se estabeleceram em Missouri, começando como um agricultor e mais tarde tornar-se rico no negócio de calçados em São Luís. Levou muitos anos para o sucesso de Eugene para neutralizar sua reputação entre amigos e colegas de Gauss. Veja também a carta de Robert Gauss para Felix Klein em 03 de setembro de 1912.
Personalidade
Gauss foi um ardente perfeccionista e um trabalhador. Ele nunca foi um escritor prolífico, recusando-se a publicar trabalhos que ele não considerou completo e acima de qualquer crítica. Isso estava de acordo com o seu lema pessoal pauca matura sed ("poucos, mas maduro"). Seus diários pessoais indicam que ele tinha feito várias importantes descobertas matemáticas anos ou décadas antes de seus contemporâneos os publicou. Historiador matemático Eric Temple Bell estimou que, Gauss tinha publicado todas as suas descobertas em tempo hábil, ele teria avançado matemática por 50 anos.
Embora ele demorou em alguns alunos, Gauss era conhecido por não gostar de ensino. Diz-se que ele participou de apenas uma única conferência científica, que estava em Berlim , em 1828. No entanto, vários de seus alunos tornaram-se influentes matemáticos, entre eles Richard Dedekind, Bernhard Riemann , e Friedrich Bessel. Antes de morrer, Sophie Germain foi recomendado por Gauss para receber seu diploma honorário.
Gauss geralmente se recusou a apresentar a intuição por trás de seus frequentemente muito elegantes provas-preferia que eles apareçam "fora do ar" e apagou todos os vestígios de como ele descobriu. Isso é justificado, se insatisfatória, por Gauss em seu " Disquisitiones Arithmeticae ", onde ele afirma que toda a análise (ou seja, os caminhos de uma viajado para alcançar a solução de um problema) deve ser suprimido por razões de brevidade.
Gauss apoiado a monarquia e oposição Napoleão , a quem ele via como uma conseqüência da revolução .
Anedotas
Existem várias histórias de sua genialidade precoce. Segundo uma delas, seus dons se tornou muito aparente com a idade de três anos quando ele corrigiu, mentalmente e sem falhas em seus cálculos, um erro seu pai tinha feito em papel, enquanto o cálculo finanças.
Outra história famosa conta que em escola primária depois de o jovem Gauss se comportado mal, seu professor, JG Büttner, deu-lhe uma tarefa: adicionar uma lista de números inteiros em progressão aritmética; como a história é mais frequentemente dito, estes foram os números de 1 a 100. O jovem Gauss supostamente produzido a resposta correta dentro de segundos, para o espanto de seu professor e seu assistente Martin Bartels.
Método presumido de Gauss foi perceber que a adição de pares de termos de extremidades opostas da lista produziu somas intermédios idênticos: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, e assim por diante, para uma soma total de 50 × 101 = 5050. No entanto, os detalhes da história são na melhor das hipóteses incerta (ver para a discussão do original Fonte Wolfgang von Sartorius Waltershausen e as mudanças nas outras versões); alguns autores, como Joseph Rotman em seu livro Um primeiro curso de Álgebra abstrata, questionam se ele tivesse acontecido.
De acordo com Isaac Asimov , Gauss uma vez foi interrompida no meio de um problema e disse que sua esposa estava morrendo. Ele é suposto ter dito: "Diga-lhe que aguarde um momento até que eu sou feito." Este episódio é brevemente discutido em De G. Waldo Dunnington Gauss, Titan da Ciência onde é sugerido que se trata de um apócrifos história.
Comemorações


De 1989 a 2001, o retrato de Gauss, uma curva de distribuição normal e alguns proeminente Edifícios Göttingen foram destaque na marca de dez notas de banco alemão. O reverso caracterizou o heliotrópio e um abordagem de triangulação para Hannover. A Alemanha também emitiu três selos postais em homenagem Gauss. One (. Não 725) apareceu em 1955 no centenário de sua morte; outros dois, nos. 1246 e 1811, em 1977, o 200º aniversário de seu nascimento.
2005 romance de Daniel Kehlmann Die Welt der Vermessung, traduzido para o Inglês como Medição do Mundo (2006), explora a vida de Gauss e trabalhar através de uma lente de ficção histórica, contrastando-as com as do explorador alemão Alexander von Humboldt.
Em 2007, uma busto de Gauss foi colocado no Templo Walhalla.
Coisas nomeadas em homenagem a Gauss incluem:
- A desmagnetização, o processo de eliminação de um campo magnético.
- O CGS unidade para campo magnético foi nomeado gauss em sua honra,
- A cratera Gauss na Lua ,
- Asteróide 1001 Gaussia,
- O navio Gauss, utilizado no Gauss expedição para a Antártida,
- Gaussberg, um vulcão extinto descoberto pela expedição acima indicado,
- Torre Gauss, uma torre de observação em Dransfeld, Alemanha ,
- Em escolas secundárias canadenses, um concurso nacional anual matemática (Concorrência Matemática Gauss) administrado pelo Centro de Educação em Matemática e Computação é nomeado em honra de Gauss,
- Em Universidade da Califórnia, Santa Cruz, em Crown College, um edifício dormitório é nomeado após ele,
- A Gauss Haus, um RMN no centro Universidade de Utah,
- O Carl-Friedrich-Gauß Escola de Matemática, Ciência da Computação, Administração de Empresas, Economia e Ciências Sociais da Universidade de Braunschweig,
- O edifício de Gauss - Universidade de Idaho (Faculdade de Engenharia).
Em 1929, o polonês matemático Marian Rejewski, que resolveria o alemão máquina Enigma cifra em dezembro de 1932, começou a estudar estatísticas atuariais na Göttingen. A pedido de sua Professor da Universidade de Poznań, Zdzisław Krygowski, ao chegar em Göttingen Rejewski depositou flores no túmulo de Gauss.
Escritos
- 1799: Tese de doutorado sobre o Teorema fundamental da álgebra, com o título: Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis em Factores reales primi vel secundi posse gradus resolvi ("Nova prova do teorema de que cada função algébrica integrante de uma variável pode ser resolvido em fatores reais ( ou seja, polinómios) do primeiro ou segundo grau ")
- 1801: Disquisitiones Arithmeticae. Tradução alemão por H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae e outros trabalhos sobre a teoria dos números) (segunda edição). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 1-453. Tradução Inglês por Arthur A. Clarke Disquisitiones Arithemeticae (segunda edição, corrigida). Nova Iorque: Springer. 1986. ISBN 0-387-96254-9.
- 1808: Theorematis arithmetici demonstratio nova. Göttingen: Comentário. Soe. Regiae sci, Göttingen XVI. Tradução alemão por H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae e outros trabalhos sobre a teoria dos números) (segunda edição). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 457-462 [introduz Lema de Gauss, usa-lo na terceira prova da reciprocidade quadrática]
- 1809: Theoria Motus Corporum Coelestium em sectionibus conicis solem ambientium (Theorie der Bewegung der Himmelskörper, die die Sonne em Kegelschnitten umkreisen), Tradução Inglês por CH Davis, reimpresso 1963, Dover, New York.
- 1811: Summatio serierun quarundam singularium. Göttingen: Comentário. Soe. Regiae sci, Göttingen. Tradução alemão por H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae e outros trabalhos sobre a teoria dos números) (segunda edição). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 463-495 [Determinação do sinal do Gauss soma quadrática, usa isso para dar a quarta prova da reciprocidade quadrática]
- 1812: Disquisitiones Generales Circa seriem infinitam
- 1818: Theorematis fundamentallis em doctrina de residuis quadraticis demonstrationes et amplicationes novae. Göttingen: Comentário. Soe. Regiae sci, Göttingen. Tradução alemão por H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae e outros trabalhos sobre a teoria dos números) (segunda edição). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 496-510 [Quinto e sexto provas de reciprocidade quadrática]
- 1821, 1823 e 1826: Theoria combinationis observationum erroribus minimis obnoxiae. Drei Abhandlungen betreffend morrer als Wahrscheinlichkeitsrechnung Grundlage des Gauß'schen Fehlerfortpflanzungsgesetzes. (Três ensaios sobre o cálculo de probabilidades como a base da lei de Gauss de propagação de erro) Tradução Inglês por GW Stewart, 1987, Sociedade de Matemática Industrial.
- 1827: Disquisitiones generales circa superficies curvas, Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores. Volume VI, pp. 99-146. " Investigações Gerais de superfícies curvas "(publicado 1965) Raven Press, New York, traduzidos por AMHiltebeitel e JCMorehead.
- 1828: Theoria biquadraticorum residuorum, Commentatio prima. Göttingen: Comentário. Soe. Regiae sci, Göttingen 6. tradução alemão por H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae e outros trabalhos sobre a teoria dos números) (segunda edição). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 511-533 [fatos elementares sobre resíduos biquadrada, prova um dos suplementos da lei de reciprocidade biquadrática (o personagem biquadrática de 2)]
- 1832: Theoria biquadraticorum residuorum, Commentatio secunda. Göttingen: Comentário. Soe. Regiae sci, Göttingen 7. tradução alemão por H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae e outros trabalhos sobre a teoria dos números) (segunda edição). New York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 534-586 [Introduz a Inteiros de Gauss, estados (sem prova) o direito de reciprocidade biquadrática, prova a lei complementar para 1 + i]
- 1843-1844: Über der Untersuchungen Gegenstände höheren Geodäsie. Erste Abhandlung, Abhandlungen der Gesellschaft der Königlichen Wissenschaften em Göttingen. Zweiter Band, pp. 3-46
- 1846-1847: Über der Untersuchungen Gegenstände höheren Geodäsie. Zweite Abhandlung, Abhandlungen der Gesellschaft der Königlichen Wissenschaften em Göttingen. Dritter Band, pp. 3-44
- Mathematisches Tagebuch 1796-1814, Ostwaldts Klassiker, Harri Deutsch Verlag 2005, mit Anmerkungen von Neumamn, ISBN 978-3-8171-3402-1 (Tradução Inglês com anotações por Jeremy Gray:. Expositiones Math 1984)
- Trabalhos coletivos Gauss estão online aqui Isto inclui traduções em alemão de textos em latim e comentários de diversas autoridades

