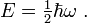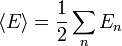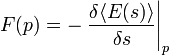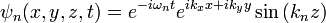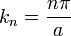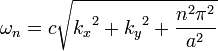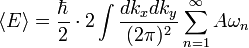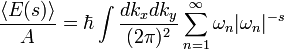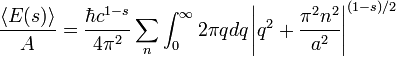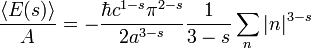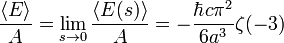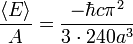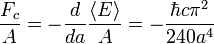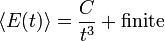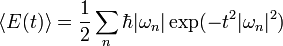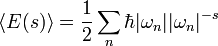Efeito Casimir

Forças de Casimir em placas paralelas.

Forças de Casimir em placas paralelas.

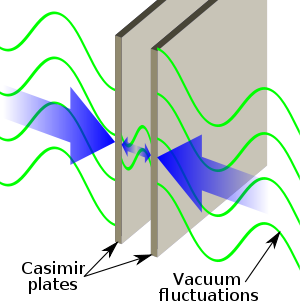
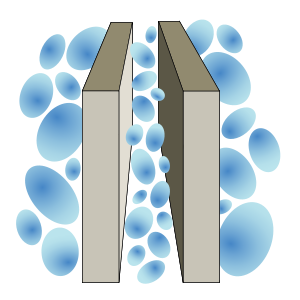
Em física , o efeito Casimir ea força de Casimir-Polder são físicos forças resultantes de um campo quantificado . O exemplo típico é de dois descarregadas placas metálicas em um vácuo, colocados alguns micrômetros de distância, sem qualquer externo campo eletromagnético. Em um descrição clássica, a ausência de um campo externo também significa que não existe um campo entre as placas, e nenhuma força seria medido entre eles. Quando este campo é estudada utilizando em vez da mecânica quântica , vê-se que as placas não afectam o virtuais fotões que constituem o campo, e geram um líquido ou uma força de atracção ou uma repulsão, dependendo do arranjo específico das duas placas. Esta força foi medido, e é um exemplo notável de um efeito puramente devido segunda quantização. (No entanto, o tratamento de condições de contorno nestes cálculos levou a alguma controvérsia.)

Holandês físicos Hendrik BG Casimir e Dirk Polder propôs pela primeira vez a existência da força e formulou um experimento para detectá-lo em 1948, durante a sua participação na investigação em Philips Research Labs. A forma clássica da experiência, descrito acima, demonstrou com sucesso a força para dentro de 15% do valor previsto pela teoria.

Uma vez que a intensidade da força diminui rapidamente com a distância, é apenas mensurável quando a distância entre os objectos é extremamente pequena. Em uma escala submicrometre, esta força se torna tão forte que ele se torne a força dominante entre os condutores não carregadas. Na verdade, em separações de 10 nm a cerca de 100-vezes o tamanho típico de uma a-átomo efeito de Casimir produz o equivalente a 1 atmosfera de pressão (101,3 kPa), o valor de precisão dependendo da geometria da superfície e outros factores .

Embora o efeito de Casimir pode ser expressa em termos de partículas virtuais que interagem com os objectos, que é melhor descrita e mais facilmente calculada em termos de energia do ponto zero de um campo quantificado no espaço intermediário entre os objetos. Em moderna física teórico, o efeito de Casimir desempenha um papel importante na modelo de saco quiral de nucleon; e em Física Aplicada, está se tornando cada vez mais importante no desenvolvimento dos componentes cada vez menores, miniaturizadas de emergentes microtecnologias e nanotecnologias.

Visão global

O efeito Casimir pode ser entendida pela idéia de que a presença de metais condutores e dieléctricos alterar o vácuo valor esperado da energia da segunda quantizado campo eletromagnético. Uma vez que o valor desta energia depende das formas e posições dos condutores e dieléctricos, o efeito de Casimir manifesta-se como uma força entre tais objectos.

Energia do vácuo

O efeito Casimir é um resultado da teoria quântica de campos , que afirma que todos os vários fundamentais campos, tais como a campo eletromagnético, deve ser quantificado em cada ponto do espaço. Numa visão simplificada, um "campo" em física pode ser visualizada como se o espaço foi preenchido com esferas interligadas e molas de vibração, e a intensidade do campo pode ser visualizado como o deslocamento de uma bola a partir da sua posição de repouso. Vibrações neste domínio propagar e são regidos pela adequada equação de onda para o campo particular em questão. O segunda quantização da teoria quântica requer que cada uma dessas combinações bola de mola ser quantizado, isto é, que a intensidade do campo ser quantizado em cada ponto no espaço. Canonicamente, o campo em cada ponto no espaço é um simples oscilador harmônico, e sua quantização coloca um oscilador harmônico quântico em cada ponto. Excitações de campo correspondem ao partículas elementares da física de partículas . No entanto, mesmo o vácuo tem uma estrutura muito complexa. Todos os cálculos de teoria quântica de campos deve ser feita em relação a este modelo do vácuo.

O vácuo tem, implicitamente, todas as propriedades que uma partícula pode ter: rotação, ou polarização no caso de luz , a energia , e assim por diante. Em média, todas essas propriedades anular: o vácuo é, afinal, "vazio" neste sentido. Uma exceção importante é o energia do vácuo ou a vácuo valor esperado da energia. A quantização de um oscilador harmônico simples afirma que a menor energia possível ou energia do ponto zero que tal um oscilador pode ter é

Somando sobre todos os osciladores possíveis em todos os pontos no espaço dá uma quantidade infinita. Para remover esse infinito, pode-se argumentar que só as diferenças de energia são fisicamente mensuráveis; este argumento é a base da teoria da renormalização . Em todos os cálculos práticos, isto é como o infinito é sempre tratado. Em um sentido mais profundo, no entanto, renormalization é insatisfatório, e a remoção deste infinito apresenta um desafio na busca de uma Teoria de Tudo. Atualmente não há nenhuma explicação convincente para o infinito como isso deve ser tratado como essencialmente zero; um valor diferente de zero é essencialmente o constante cosmológica e qualquer valor grande causa problemas em cosmologia .

O efeito Casimir

A observação de Casimir foi que a campo electromagnético segundo quantum-quantizado, na presença de corpos granel, tais como metais ou dielétricos, deve obedecer o mesmo condições de contorno que o campo eletromagnético clássico deve obedecer. Em particular, esta afecta o cálculo da energia de vácuo na presença de um condutor ou dielétrico.

Considere-se, por exemplo, o cálculo do valor esperado de vácuo do campo electromagnético dentro de uma cavidade de metal, tal como, por exemplo, uma cavidade radar ou um microonda guia de ondas. Neste caso, a maneira correta de encontrar a energia do ponto zero do campo é a soma das energias do ondas da cavidade de pé. Para cada possível onda estacionária corresponde uma energia; dizem que a energia do n º onda estacionária é 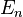. O valor esperado de vácuo a energia do campo electromagnético na cavidade é então

com a soma parcial sobre todos os valores possíveis de n enumerando as ondas estacionárias. O factor de 1/2 corresponde ao facto de as energias de ponto zero são somados (que é o mesmo 1/2 como aparece na equação 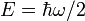). Escrito desta forma, esta soma é claramente divergente; no entanto, ele pode ser usado para criar expressões finitas.

Em particular, pode perguntar como a energia do ponto zero, depende da forma da cavidade s. Cada nível de energia 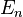depende da forma, e por isso deve-se escrever 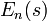para o nível de energia, e 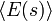para o valor esperado de vácuo. Neste ponto, surge uma observação importante: a força no ponto P sobre a parede da cavidade é igual à variação na energia do vácuo, se a forma S de parede é perturbado um pouco, por dizer 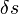, No ponto p. Ou seja, tem-se

Este valor é finito em muitos cálculos práticos.

Cálculo de Casimir

No cálculo original feita por Casimir, considerou o espaço entre um par de placas metálicas que conduzem a uma distância distante. Neste caso, as ondas estacionárias são particularmente fácil de calcular, uma vez que o componente transversal do campo eléctrico e o componente normal do campo magnético devem desaparecer na superfície de um condutor. Supondo que as placas paralelas se encontram no plano xy, as ondas estacionárias são

onde 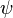representa o componente eléctrico do campo electromagnético, e, por questões de brevidade, o polarização e os componentes magnéticos são ignorados aqui. Aqui, 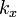e 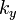são o vectores de onda em direcções paralelas às placas, e

é o vector de onda perpendicular às placas. Aqui, n é um número inteiro, resultante da exigência de que ψ desaparecem nas placas de metal. A energia dessa onda é

em que c é a velocidade da luz . A energia do vácuo é, então, a soma sobre todos os modos possíveis de excitação

onde A é a área das placas de metal, e um factor de 2 é introduzida para as duas polarizações possíveis da onda. Esta expressão é claramente infinito, e prosseguir com o cálculo, é conveniente introduzir um regulador (discutido em maior detalhe abaixo). O regulador vai servir para fazer a expressão finita, e no final será removido. O versão da energia zeta-regulada por área de unidade da placa está

No final, o limite 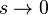é para ser tomada. Aqui s é apenas um número complexo , não deve ser confundida com a forma discutido anteriormente. Esta / soma integral é finita para s verdadeiro e maior do que 3. A soma tem um pólo em s = 3, mas pode ser analiticamente continuou a s = 0, onde a expressão é finito. Expandir este, obtém-se

onde as coordenadas polares 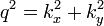foram introduzidos para transformar o integrante dupla em um único integrante. O 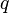em frente é o Jacobiano, eo vem da integração angular. A integral é facilmente realizada, resultando em

A soma pode ser entendido como sendo o Função zeta de Riemann, e assim um tem

Mas 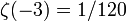e assim obtém-se

A força de Casimir por unidade de área 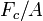para idealizada, realizando perfeitamente placas com vácuo entre eles é

onde

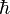(Hbar, ℏ) é a redução constante de Planck,

é a velocidade da luz ,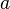

é a distância entre as duas placas.

A força é negativo, indicando que a força é atraente: movendo as duas placas mais próximas, a energia é reduzido. A presença de 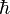mostra que a força de Casimir por unidade de área 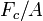é muito pequena, e que, além disso, a força é inerentemente de origem mecânica quântica.

Teoria mais recente

Uma análise muito completa do efeito de Casimir, a distâncias curtas baseia-se uma análise detalhada da força de van der Waals por Lifshitz. Usando esta abordagem, as complicações das superfícies limitantes, tais como as modificações na força de Casimir, devido à condutividade finito pode ser calculado numericamente utilizando as funções dieléctricos complexos tabelados dos materiais delimitadoras. Além destes factores, complicações surgem devido à rugosidade da superfície da fronteira e para a geometria efeitos, tais como o grau de paralelismo das placas de delimitação.

Para separações em grandes limites, o efeito de retardação dar origem a uma interacção de longo alcance. Para o caso de duas placas paralelas compostos de metais ideais em vácuo, para reduzir os resultados de Casimir.

Medição

Um dos primeiros testes experimentais foi conduzido por Marcus Sparnaay na Philips em Eindhoven, em 1958, em um experimento delicado e difícil, com placas paralelas, a obtenção de resultados não em contradição com a teoria Casimir, mas com grandes erros experimentais.

O efeito Casimir foi medido com mais precisão em 1997 por Steve K. Lamoreaux de Los Alamos National Laboratory e por Umar Mohideen e Anushree Roy do Universidade da Califórnia em Riverside. Na prática, em vez de utilizar duas placas paralelas, o que exigiria alinhamento fenomenalmente precisas para garantir que eles eram paralelas, as experiências usar uma placa que é plana e uma outra placa, que é uma parte de uma esfera com um grande raio. Em 2001, um grupo no Universidade de Pádua, finalmente, conseguiram medir a força de Casimir entre as placas paralelas utilizando microresonators.

Regularização

A fim de ser capaz de realizar cálculos, no caso geral, é conveniente introduzir um regulador nos somatórios. Este é um dispositivo artificial, usado para fazer as somas finito para que possam ser mais facilmente manipulados, seguido pela obtenção de um limite de modo a remover o regulador.

O kernel do calor ou exponencialmente soma é regulamentado

onde o limite 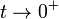é tomada no final. A divergência da soma é tipicamente manifestada como

para cavidades tridimensionais. A parte da soma infinita está associada com a constante C granel que não depende da forma da cavidade. A parte interessante da soma é a parte finita, que é dependente da forma. O Regulador Gaussian

é mais adequado para cálculos numéricos devido às suas propriedades superiores de convergência, mas é mais difícil de utilizar em cálculos teóricos. Outros, apropriadamente lisas, os reguladores podem também ser usadas. O regulador de função zeta

é completamente inadequado para cálculos numéricos, mas é bastante útil em cálculos teóricos. Em particular, as divergências mostrar-se como pólos no plano complexo s , com a divergência granel em s = 4. Esta soma pode ser analiticamente continuou passado este pólo, para obter uma parte finita em s = 0.

Não cada configuração cavidade leva necessariamente a uma parte finita (a falta de um pólo em s = 0) ou infinitas partes independentes de forma. Neste caso, deve ser entendido que a física adicional tem de ser tida em conta. Em particular, a frequências extremamente grandes (acima do plasma de freqüência), os metais tornam-se transparentes para os fótons (como raios-X), e dieléctricos mostram um ponto de corte em função da frequência, bem. Esta dependência frequência age como um regulador natural. Há uma variedade de efeitos em massa em física do estado sólido, matematicamente muito semelhante ao efeito de Casimir, onde o freqüência de corte entra em jogo explícita para manter expressões finitas. (Estes são discutidos em maiores detalhes em Landau e Lifshitz, "Teoria da mídia contínua".)

Generalidades

O efeito Casimir também pode ser calculado usando os mecanismos matemáticos de integrais funcionais da teoria quântica de campos, embora tais cálculos são consideravelmente mais abstrato e, portanto, difícil de compreender. Além disso, eles podem ser aplicados apenas a mais simples das geometrias. No entanto, o formalismo da teoria quântica de campos deixa claro que as somas de valor expectativa de vácuo estão em um certo sentido somatórios sobre os chamados " partículas virtuais ".

Mais interessante é o entendimento de que as somas sobre as energias de ondas estacionárias deve ser formalmente entendida como somas sobre os valores próprios de uma Hamiltoniano. Isso permite que os efeitos atômicos e moleculares, como a força de van der Waals , deve ser entendida como uma variação sobre o tema do efeito Casimir. Assim, considera-se o hamiltoniano de um sistema como uma função do arranjo de objectos, tais como átomos, em espaço de configuração. A alteração na energia do ponto zero como uma função de alterações da configuração pode ser entendida para resultar em forças que actuam entre os objectos.

No modelo de saco quiral de nucleão, a energia de Casimir desempenha um papel importante na mostrando a massa do nucleão é independente do raio saco. Além disso, o assimetria espectral é interpretado como um valor diferente de zero expectativa de vácuo do número de bárions, o cancelamento da número de enrolamento topológica do campo pião em torno do nucleon.

Efeito Casimir e buracos de minhoca

Matéria exótica com densidade de energia negativa é necessário para estabilizar uma buraco de minhoca. Morris, Thorne e Yurtsever salientado que a mecânica quântica do efeito de Casimir pode ser usado para produzir uma região localmente massa-negativa de espaço-tempo, e sugeriu que efeito negativo pode ser utilizado para estabilizar um buraco negro para permitir mais rápido do que viajar luz. Este foi utilizado na urdidura nova velocidade por Travis S. Taylor.

Analogias

Uma análise semelhante pode ser usada para explicar Hawking radiação que provoca a lenta " evaporação "de buracos negros (embora isto geralmente é visualizada como o escape de uma partícula de um particle- virtual par antipartícula, a outra partícula de ter sido capturada pelo buraco negro).

Reversão

Através da utilização de um perfeito lente (um com a capacidade de focar uma imagem com resolução sem restrições pelo comprimento de onda da luz) com um negativo índice de refracção, o efeito pode ser invertido, fazendo com que pequenos objectos a ser repelida em vez de atraído. No entanto, por causa da escala em que se aplica o efeito, as suas aplicações são mais susceptíveis de ser encontrado em nanotecnologia. Segundo o professor Ulf Leonhardt e Thomas Philbin Dr de Escola de Física e Astronomia da Universidade, é teoricamente possível para levitar objetos tão grandes quanto os seres humanos, mas os cientistas estão longe de desenvolver a tecnologia para tais proezas.

Aplicações

Tem sido sugerido que as forças de Casimir têm aplicação em nanotecnologia, em particular micro e nanoelectromechanical sistemas baseados em tecnologia de circuito integrado de silício, e os chamados osciladores Casimir.

Tecnologia

The Economist, 24-30 maio de 2008, com destaque para as aplicações práticas do Efeito Casimir. Casimir "stiction", que é o foco do presente artigo afecta os desenhos dos mais pequenos chips de computador. Além disso, Casimir "repulsa", que ocorre quando um líquido entre as placas promove uma força de repulsão electromagnética que pode ser útil em nanomecânica.

Filosofia

Porque o efeito Casimir se baseia no fato de que algo comumente aparece em existência do vácuo, o efeito Casimir é usado por alguns como um argumento em apoio de uma origem puramente natural para o universo.

Cultura popular

Em relação a ficção, embora a natureza do efeito não foi revelado ainda, durante um vídeo de orientação da série de TV Perdido, um Iniciativa Dharma médico (Dr. Edgar Halliwax) afirma que a ilha apresenta um "efeito Casimir." Isso pode explicar por que a Ilha apresenta qualidades temporais estranhas como deslocamento temporal a partir do resto do mundo. No episódio final da quarta temporada, o efeito foi elaborado em por a menção de um "pocket de matéria exótica com carga negativa" e uma ocorrência aparente de viagem no tempo.