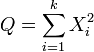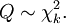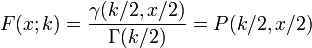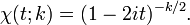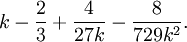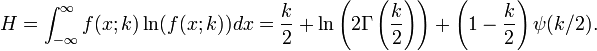Distribuição qui-quadrado
Você sabia ...
Esta seleção Escolas foi originalmente escolhido pelo SOS Children para as escolas no mundo em desenvolvimento sem acesso à internet. Ele está disponível como um download intranet. SOS Children trabalha em 45 países africanos; você pode ajudar uma criança em África ?
Função densidade de probabilidade 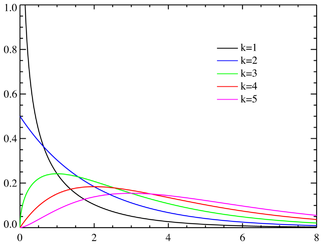 | |
Função de distribuição cumulativa 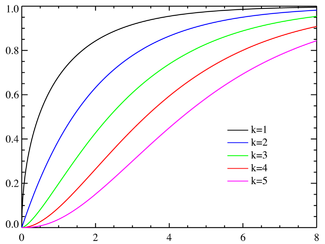 | |
| Parâmetros | 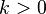 graus de liberdade graus de liberdade |
|---|---|
| Apoio | 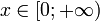 |
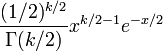 | |
| CDF | 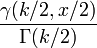 |
| Significar | 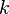 |
| Mediano | aproximadamente 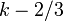 |
| Modo | 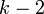 se se 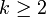 |
| Variação | 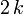 |
| Assimetria | 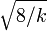 |
| Ex. curtose | 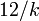 |
| Entropy | 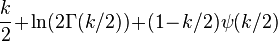 |
| MGF | 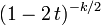 para para 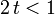 |
| CF | 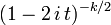 |
Em teoria da probabilidade e estatística , a distribuição qui-quadrado (também qui-quadrado ou 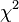 distribuição) é um dos mais amplamente utilizados teóricas distribuições de probabilidades em estatística inferencial, por exemplo, em testes de significância estatística. Ele é útil porque, sob suposições razoáveis, quantidades facilmente calculados pode ser provado ter distribuições que aproximados para a distribuição qui-quadrado, se o hipótese nula é verdadeira.
distribuição) é um dos mais amplamente utilizados teóricas distribuições de probabilidades em estatística inferencial, por exemplo, em testes de significância estatística. Ele é útil porque, sob suposições razoáveis, quantidades facilmente calculados pode ser provado ter distribuições que aproximados para a distribuição qui-quadrado, se o hipótese nula é verdadeira.
Se 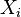 são k , independentes normalmente distribuídas variáveis aleatórias com média 0 e variância 1, então a variável aleatória
são k , independentes normalmente distribuídas variáveis aleatórias com média 0 e variância 1, então a variável aleatória
é distribuído de acordo com a distribuição qui-quadrado. Isso geralmente é escrito
A distribuição qui-quadrado tem um parâmetro:  - Um número inteiro positivo, que especifica o número de graus de liberdade (isto é, o número de
- Um número inteiro positivo, que especifica o número de graus de liberdade (isto é, o número de 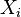 )
)
A distribuição do Qui-quadrado é um caso especial do distribuição gama.
As situações mais conhecidos em que a distribuição qui-quadrado são usados são o comum testes qui-quadrado para bondade de ajuste de uma distribuição observada para uma teórica, e do independência dos dois critérios de classificação de dados qualitativos. No entanto, muitos outros testes estatísticos levar a uma utilização desta distribuição. Um exemplo é Análise de Friedman de variância por postos.
Características
Função densidade de probabilidade
A função densidade de probabilidade da distribuição qui-quadrado é
onde 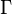 indica o Função Gamma, que leva valores particulares nas meias-inteiros.
indica o Função Gamma, que leva valores particulares nas meias-inteiros.
Função de distribuição cumulativa
Sua função de distribuição cumulativa é:
onde 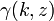 é o baixa função Gamma incompleta e
é o baixa função Gamma incompleta e 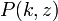 é o função Gamma regularizada.
é o função Gamma regularizada.
Tabelas dessa distribuição - geralmente na sua forma cumulativa - estão amplamente disponíveis ea função é incluído em muitos planilhas e tudo pacotes estatísticos.
Função característica
O função característica da distribuição qui-quadrado é
Propriedades
A distribuição qui-quadrado tem inúmeras aplicações em inferencial estatísticas , por exemplo em testes qui-quadrado e para a estimativa desvios . Entra o problema de calcular a média de uma população normalmente distribuídos e o problema de estimar a inclinação de uma regressão linha através do seu papel na distribuição t de Student . Ele entra tudo A análise de variância problemas através do seu papel na F-distribuição, que é a distribuição da relação de dois qui-quadrado independentes variáveis aleatórias divididos pelos seus respectivos graus de liberdade.
Aproximação normal
Se 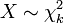 , Em seguida, como
, Em seguida, como  tende para o infinito, a distribuição de
tende para o infinito, a distribuição de 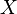 tende a normalidade. No entanto, a tendência é lento (a assimetria é
tende a normalidade. No entanto, a tendência é lento (a assimetria é 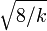 eo excesso de curtose é
eo excesso de curtose é 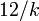 ) E duas transformações são normalmente considerados, cada uma das quais se aproxima de normalidade mais rápido do que
) E duas transformações são normalmente considerados, cada uma das quais se aproxima de normalidade mais rápido do que 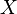 si:
si:
Fisher mostrou empiricamente que 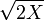 é aproximadamente normalmente distribuído com média
é aproximadamente normalmente distribuído com média 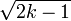 e uma unidade de desvio. É possível chegar ao mesmo resultado aproximação normal usando momento correspondente. Para ver isto, considere a média ea variância de uma variável aleatória Chi-distribuídos
e uma unidade de desvio. É possível chegar ao mesmo resultado aproximação normal usando momento correspondente. Para ver isto, considere a média ea variância de uma variável aleatória Chi-distribuídos 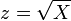 , Que são dadas por
, Que são dadas por 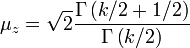 e
e 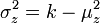 , Onde
, Onde 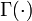 é a função Gama. A proporção particular de as funções Gamma em
é a função Gama. A proporção particular de as funções Gamma em 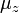 tem a seguinte série de expansão :
tem a seguinte série de expansão :
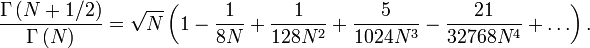 Quando
Quando 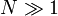 , Esta proporção pode ser estimado da seguinte forma:
, Esta proporção pode ser estimado da seguinte forma: 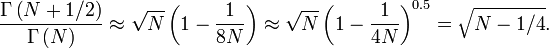
Então, momento simples resultado de acordo no seguinte aproximação das 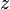 :
: 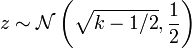 , A partir do qual se segue que
, A partir do qual se segue que 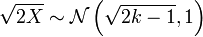 .
.
Wilson e Hilferty mostrou em 1931 que ![\ Sqrt [3] {X / k}](../../images/185/18595.png) é aproximadamente normalmente distribuído com média
é aproximadamente normalmente distribuído com média 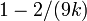 e variância
e variância 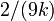 .
.
O valor esperado de uma variável aleatória de distribuição qui-quadrado com  graus de liberdade é
graus de liberdade é  ea variância é
ea variância é 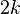 . A mediana é dada aproximadamente por
. A mediana é dada aproximadamente por
Note-se que dois graus de liberdade de chumbo para uma distribuição exponencial .
Informações entropia
O entropia da informação é dada pela
onde 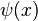 é o Digamma função.
é o Digamma função.
Distribuições relacionados
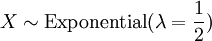 é uma distribuição exponencial se
é uma distribuição exponencial se 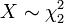 (Com dois graus de liberdade).
(Com dois graus de liberdade). 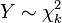 é uma distribuição qui-quadrado se
é uma distribuição qui-quadrado se 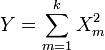 para
para 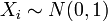 independente, que são normalmente distribuídos .
independente, que são normalmente distribuídos . - Se o
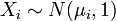 têm meios diferentes de zero, em seguida,
têm meios diferentes de zero, em seguida, 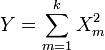 é desenhado a partir de um distribuição qui-quadrado não central.
é desenhado a partir de um distribuição qui-quadrado não central. - A distribuição qui-quadrado
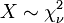 é um caso especial do distribuição gama, em que
é um caso especial do distribuição gama, em que 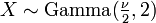 .
. 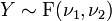 é um F-distribuição se
é um F-distribuição se 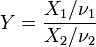 onde
onde 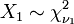 e
e 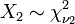 são independentes com os respectivos graus de liberdade.
são independentes com os respectivos graus de liberdade. 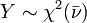 é uma distribuição qui-quadrado se
é uma distribuição qui-quadrado se 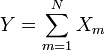 onde
onde 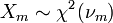 são independentes e
são independentes e 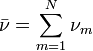 .
. - se
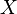 é distribuído qui-quadrado, em seguida,
é distribuído qui-quadrado, em seguida, 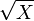 é chi distribuído.
é chi distribuído. - em particular, se
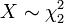 (Qui-quadrado com 2 graus de liberdade), em seguida,
(Qui-quadrado com 2 graus de liberdade), em seguida, 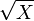 é Rayleigh distribuído.
é Rayleigh distribuído. - se
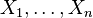 são iid
são iid 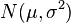 variáveis aleatórias , em seguida,
variáveis aleatórias , em seguida, 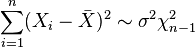 onde
onde 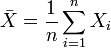 .
. - se
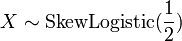 , Então
, Então 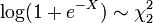
| Nome | Estatística |
|---|---|
| distribuição qui-quadrado | 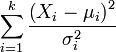 |
| qui-quadrado não central de distribuição | 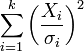 |
| distribuição chi | 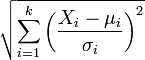 |
| distribuição chi não central | 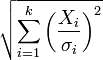 |