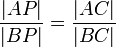Círculo
Informações de fundo
Este conteúdo da Wikipedia foi escolhida pela SOS Children para adequação nas escolas ao redor do mundo. Clique aqui para saber mais sobre apadrinhamento de crianças.
| Círculo | |
|---|---|
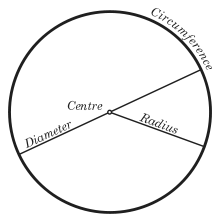 Ilustração círculo mostrando um raio, diâmetro, no centro, e da circunferência | |
| Área | 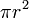 (Em que r = raio) (Em que r = raio) |

Um círculo é um simples forma da geometria euclidiana que é o conjunto de tudo Os pontos em um plano que são de uma determinada distância a partir de um determinado ponto, o centro. A distância entre qualquer um dos pontos e o centro é chamado o raio. Também pode ser definido como o locus de um ponto equidistante de um ponto fixo.
Um círculo é uma fechada simples curva que divide o plano em duas regiões: uma interior e um exterior. No uso diário, o termo "circunferência" podem ser utilizados indiferentemente para se referir a qualquer um dos limites da figura, ou para toda a figura incluindo o seu interior; no uso da técnica rigorosa, o círculo é o primeiro eo último é chamado de disco.
Um círculo pode ser definida como a curva traçada por um ponto que se move de modo que a sua distância a partir de um determinado ponto é constante.
Um círculo pode também ser definido como uma especial elipse , em que os dois focos são coincidentes e a excentricidade é 0. Os círculos são cónicas atingidos quando um cone circular direito é intersectada por um plano perpendicular ao eixo do cone.
Terminologia
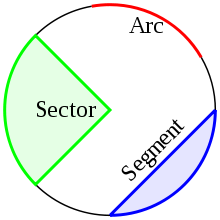
- Arc: qualquer parte ligada de circunferência do círculo.
- Centro: o ponto equidistante dos pontos da circunferência.
- Chord: um segmento de linha cujo endpoints mentir sobre o círculo.
- Circunferência: o comprimento de um circuito ao longo do círculo.
- Diâmetro : a corda mais longa, um segmento de linha cujas extremidades se encontram no círculo e que passa através do centro; ou o comprimento de um tal segmento, que é a maior distância entre quaisquer dois pontos no círculo.
- Raio: um segmento de recta que une o centro do círculo para qualquer ponto no próprio circulo; ou o comprimento de um tal segmento, que é metade de um diâmetro.
- Secante: uma corda estendida, uma linha reta cortar o círculo em dois pontos.
- Sector: uma região delimitada por dois raios e um arco encontra-se entre os raios.
- Segmento: uma região delimitada por uma corda e um arco que se encontra entre pontos de extremidade da corda.
- Semicírculo: a região limitada por um diâmetro e um arco que se encontra entre pontos de extremidade do diâmetro. Ele é um caso especial de um segmento.
- Tangent : uma linha reta que toca o círculo em um único ponto.
 |
 |
História
A palavra "círculo" deriva do grego, Kirkos "um círculo," a partir da base de ker- o que significa para virar ou dobrar. As origens das palavras " circo "e" circuito "estão intimamente relacionados.

O círculo foi sabido desde que antes do início da história registrada. Círculos naturais teriam sido observadas, como a Lua, Sol, ea uma curta haste da planta soprando no vento na areia, que forma uma forma do círculo na areia. O círculo é a base para a roda , o que, com os inventos relacionados, tais como engrenagens, torna muito da maquinaria moderna possível. Em matemática, o estudo do círculo ajudou a inspirar o desenvolvimento da geometria, astronomia , e cálculo.
Cedo ciência , particularmente geometria e astrologia e astronomia, estava ligado ao divino para a maioria eruditos medievais, e muitas acreditaram que havia algo intrinsecamente "divino" ou "perfeito" que poderia ser encontrado nos círculos.
 O bússola neste manuscrito do século 13 é um símbolo do ato de Deus Criação. Observe também a forma circular da halo
O bússola neste manuscrito do século 13 é um símbolo do ato de Deus Criação. Observe também a forma circular da halo
 Tughrul Torre de dentro
Tughrul Torre de dentro
 Círculos em um desenho astronômico velho árabe
Círculos em um desenho astronômico velho árabe
Alguns destaques na história do círculo são:
- 1700 aC - A Rhind papiro dá um método para localizar a área de um campo circular. O resultado corresponde a 256/81 (3,16049 ...) como um valor aproximado de π.
- 300 aC - Livro 3 de Elementos de Euclides lida com as propriedades dos círculos.
- Em Platão 's Sétima Carta existe uma definição detalhada e explicação do círculo. Platão explica o círculo perfeito, e como ele é diferente de qualquer desenho, palavras, definição ou explicação.
- 1880 CE- Lindemann prova que π é transcendental, efetivamente resolver o problema milenar de quadratura do círculo.
Resultados analíticos
Comprimento da circunferência
A proporção de um círculo de circunferência ao seu diâmetro é π (PI), um irracional constante aproximadamente igual a 3,141592654. Assim, o comprimento da circunferência C está relacionada com o raio r e o diâmetro d em:
Área fechada
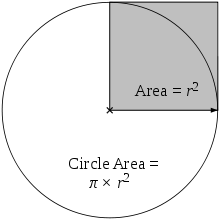
Como provado por Arquimedes, o área delimitada por um círculo que é igual a de um triângulo cuja base tem o comprimento da circunferência do círculo e cuja altura é igual raio do círculo, que trata de π multiplicado pelo raio ao quadrado:
Equivalentemente, denotando diâmetro por d,
que é, aproximadamente 79 por cento do quadrado circunscrito (cujo lado tem um comprimento d).
O círculo é a curva plana envolvendo a área máxima para um dado comprimento do arco. Isto relaciona-se o círculo para um problema no cálculo das variações , a saber, a isoperimétrica desigualdade.
Equações
Coordenadas cartesianas
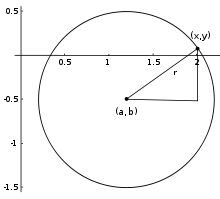
Em um x - y sistema de coordenadas cartesianas , o círculo com centro coordenadas (a, b) e raio r é o conjunto de todos os pontos (x, y) tais que
Esta equação , também conhecida como a equação de círculo, se segue a partir do Teorema de Pitágoras aplicado a qualquer ponto no círculo: como mostrado na figura, para a direita, o raio é a hipotenusa de um triângulo rectângulo cujos outros lados são de comprimento x - a e y - b. Se o círculo está centrado na origem (0, 0), então a equação é simplificada
A equação pode ser escrita em forma paramétrica usando o funções trigonométricas seno e cosseno como
onde t é a paramétrico variável no intervalo de 0 a 2π, interpretada geometricamente como o ângulo que o raio a partir de (a, b) para (x, y) faz com o eixo x. Uma alternativa parametrização do círculo é:
Neste parametrização, a proporção de T para R pode ser interpretado como o geometricamente projeção estereográfica do círculo para a linha que passa pelo centro paralelo ao eixo x.
Em coordenadas homogêneas cada seção cônica com a equação de um círculo é da forma
Pode ser provado que uma cónica é um círculo exatamente quando ele contém (quando estendida ao plano projetivo complexo) os pontos I (1: i: 0) e J (1: - i: 0). Estes pontos são chamados a pontos circulares no infinito.
Coordenadas polares
Em coordenadas polares a equação de um círculo é:
onde a é o raio do círculo, 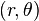 é a de coordenadas polares de um ponto genérico no círculo, e
é a de coordenadas polares de um ponto genérico no círculo, e 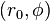 é o de coordenadas polares do centro do círculo (ou seja, r é 0 a distância a partir da origem para o centro do círculo, e φ é o ângulo no sentido contrário a partir do -axis x positiva para a linha de ligação da origem até ao centro de o círculo). Para um círculo centrado na origem, ou seja, r 0 = 0, o que reduz simplesmente r = a. Quando r = 0 um, ou quando a origem reside no círculo, a equação torna-se
é o de coordenadas polares do centro do círculo (ou seja, r é 0 a distância a partir da origem para o centro do círculo, e φ é o ângulo no sentido contrário a partir do -axis x positiva para a linha de ligação da origem até ao centro de o círculo). Para um círculo centrado na origem, ou seja, r 0 = 0, o que reduz simplesmente r = a. Quando r = 0 um, ou quando a origem reside no círculo, a equação torna-se
No caso geral, a equação pode ser resolvida para r, dando
a solução com um sinal de menos na frente da raiz quadrada dando a mesma curva.
Plano complexo
No plano complexo , um círculo com um centro em C e o raio (r) tem a equação 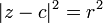 . Na forma paramétrica isto pode ser escrito
. Na forma paramétrica isto pode ser escrito 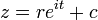 .
.
A equação generalizada ligeiramente 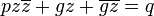 para real p, q e g complexo às vezes é chamado de círculo generalizada. Isto torna-se a equação anterior para um círculo com
para real p, q e g complexo às vezes é chamado de círculo generalizada. Isto torna-se a equação anterior para um círculo com 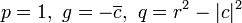 , Desde
, Desde 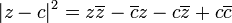 . Nem todos os círculos generalizadas são realmente círculos: um círculo generalizada ou é um (verdadeiro) círculo ou uma linha .
. Nem todos os círculos generalizadas são realmente círculos: um círculo generalizada ou é um (verdadeiro) círculo ou uma linha .
Retas tangentes
A linha tangente por meio de um ponto P sobre o círculo é perpendicular ao diâmetro que passa por P. Se P = (x 1, y 1) e o centro do círculo tem (a, b) e raio r, então a linha tangente é perpendicular à linha entre (a, b) (x 1, y 1), por isso tem a forma (x 1 - a) x + (y 1 - b) y = c. Avaliando em (x 1, y 1) determina o valor de C e o resultado é que a equação da tangente é
ou
Se y 1 ≠ B, então a inclinação desta linha é
Isto também pode ser encontrado usando diferenciação implícita.
Quando o centro do círculo está na origem, em seguida, a equação da linha tangente se torna
e a sua inclinação é
Propriedades
- O círculo é a forma com a maior área para um dado comprimento de perímetro. (Ver Desigualdade isoperimétrica.)
- O círculo é uma forma altamente simétrica: cada linha através do centro forma uma linha de simetria de reflexão e tem simetria de rotação em torno do centro de todos os ângulos. Sua grupo representa a simetria O grupo ortogonal (2, R). O grupo de rotações por si só é o grupo círculo T.
- Todos os círculos são semelhante.
- Circunferência e raio de um círculo são proporcional.
- A área fechada e o quadrado de seu raio são proporcional.
- O As constantes de proporcionalidade são 2π e π, respectivamente.
- O círculo que é centrado na origem com raio 1 é chamado de círculo unitário.
- Pensado como uma grande círculo do esfera unitária, torna-se o Círculo de Riemann.
- Através de qualquer um dos três pontos, nem todos na mesma linha, encontra-se um único círculo. Em coordenadas cartesianas , é possível dar fórmulas explícitas para as coordenadas do centro do círculo e o raio em termos das coordenadas dos três pontos indicados. Ver circumcircle.
Acorde
- Acordes são equidistantes do centro de um círculo se e somente se eles são iguais em comprimento.
- A mediatriz de um acorde passa pelo centro de um círculo; declarações equivalentes decorrentes da exclusividade da mediatriz:
- Uma linha perpendicular a partir do centro de um círculo bissecta o acorde.
- O segmento de linha ( segmento circular) através do centro que bissecta um acorde é perpendicular à corda.
- Se um ângulo central e um ângulo inscrito de um círculo são subtendido pela mesma corda e sobre o mesmo lado da corda, em seguida, o ângulo central é duas vezes o ângulo inscrito.
- Se dois ângulos são inscritos na mesma corda e sobre o mesmo lado da corda, em seguida, eles sejam iguais.
- Se dois ângulos são inscritos na mesma corda e em lados opostos da corda, em seguida, eles são complementares.
- Para um quadrilátero cíclico, o ângulo externo é igual ao ângulo oposto interior.
- Um ângulo inscrito subtendido por um diâmetro é um ângulo reto (ver Thales 'teorema).
- O diâmetro da corda é maior do círculo.
- Se a intersecção de quaisquer dois acordes divide uma corda em comprimentos A e B e divide a outra corda em comprimentos c e d, em seguida, ab = cd.
- Se a intersecção de quaisquer dois acordes perpendiculares divide uma corda em comprimentos A e B e divide o outro acorde em comprimentos c e d, em seguida, um 2 + b 2 + C 2 + d 2 é igual ao quadrado do diâmetro.
- A soma dos comprimentos de quadrados de quaisquer duas cordas que se intersectam em ângulos rectos a um dado ponto é a mesma que a de qualquer outras duas cordas que se intersectam no mesmo ponto, e é dada por R 8 2-4 p 2 (em que r é a p e raio do círculo é a distância entre o ponto central do ponto de cruzamento).
- A distância a partir de um ponto na circunferência para uma determinada corda vezes o diâmetro do círculo é igual ao produto das distâncias a partir do ponto de as extremidades da corda.
Sagitta
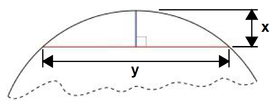
- O sagitta (também conhecido como o verseno) é um segmento de linha traçada perpendicularmente a uma corda, entre o ponto médio da referida corda e do arco de círculo.
- Dado o comprimento de y de uma corda, e o comprimento x da sagitta, o teorema de Pitágoras pode ser utilizada para calcular o raio do círculo único, que se encaixam em torno de duas linhas:
Uma outra prova de que este resultado se baseia apenas em duas propriedades de acorde dadas acima é como se segue. Dada uma corda de comprimento y e com sagitta de comprimento x, uma vez que o sagitta intercepta o ponto central do acorde, sabemos que ele é parte de um diâmetro do círculo. Uma vez que o diâmetro é duas vezes o raio, a parte "em falta" do diâmetro é (2 R - X) em comprimento. Usando o facto de uma parte de uma corda vezes a outra parte é igual ao mesmo produto tomado ao longo de uma corda que intersecta a primeira corda, descobrimos que (2 r - x) x = (y / 2) 2. Resolvendo para r, encontramos o resultado necessário.
Tangente
- A linha perpendicular traçada a um raio através do ponto de extremidade do raio é tangente ao círculo.
- Uma linha traçada perpendicularmente para uma tangente que passa pelo ponto de contacto com um círculo passa através do centro do círculo.
- Dois tangentes sempre pode ser desenhada para um círculo a partir de qualquer ponto situado fora do círculo, e estes tangentes são iguais em comprimento.
- Se uma tangente em A e uma tangente em B se cruzam no ponto P exterior, em seguida, denotando o centro como O, os ângulos ∠ ∠ BOA e BPA são suplementar.
- Se AD é tangente ao círculo em A e se AQ é uma corda do círculo, em seguida, ∠ DAQ = 1/2 arco (AQ).
Teoremas

- O teorema afirma que se acorde dois acordes, CD e EB, se cruzam em A, então CA × DA = EA × BA.
- Se uma tangente do ponto D externo encontra o círculo na C e uma secante do ponto D externo encontra o círculo em G e E, respectivamente, em seguida, DC = 2 × DG DE. (Teorema Tangent-secante.)
- Se duas secantes, DG e DE, também cortar o círculo em H e F, respectivamente, então DH × DG = DF × DE. (Corolário do teorema tangente-secante.)
- O ângulo entre a tangente e acorde é igual a metade do ângulo subtendido no lado oposto da corda (Tangente acorde Ângulo).
- Se o ângulo subtendido pela corda no centro é de 90 graus, então L = r √2, onde L é o comprimento da corda e r é o raio do círculo.
- Se duas secantes são inscritos no círculo como mostrado à direita, em seguida, a medição do ângulo A é igual a metade da diferença das medidas dos arcos fechados (DE e BC). Este é o teorema secante-secante.
Ângulos inscritos
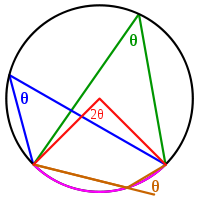
Um ângulo inscrito (exemplos são os ângulos azuis e verdes na figura) é exactamente a metade do correspondente ângulo central (vermelho). Assim, todos os ângulos inscritos que subtender o mesmo arco (rosa) são iguais. Ângulos inscritos no arco (marrom) são suplementares. Em particular, cada ângulo inscrito que subtende um diâmetro é um ângulo recto (uma vez que o ângulo central é de 180 graus).
Círculo de Apolônio
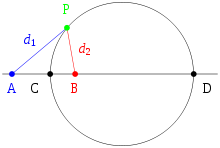
Apolônio de Perga mostrou que um círculo também pode ser definida como um conjunto de pontos num plano tendo uma razão constante (diferente de 1) de distâncias para dois focos fixos, A e B. (O conjunto de pontos onde as distâncias são iguais é a mediatriz de A e B, uma linha.) Esse círculo é dito às vezes ser desenhado sobre dois pontos.
A prova está em duas partes. Em primeiro lugar, deve-se provar que, tendo em conta dois focos A e B e uma proporção de distâncias, qualquer ponto P satisfazendo a relação de distâncias deve cair sobre um círculo em particular. Seja C um outro ponto, também satisfazendo a relação e deitado no segmento AB. Pelo bissetriz teorema do PC segmento de linha será bifurcar o interior ângulo APB, uma vez que os segmentos são semelhantes:
Analogamente, uma PD segmento de linha por meio de algum ponto D na AB prorrogado corta o correspondente exterior ângulo BPQ onde Q está no AP prorrogado. Uma vez que os ângulos interiores e exteriores resumir a 180 graus, o ângulo de CPD é exactamente 90 graus, ou seja, uma ângulo direito. O conjunto de pontos P tais que ângulo CPD é um ângulo reto forma um círculo, de que CD é um diâmetro.
Em segundo lugar, ver uma prova de que cada ponto no círculo indicado satisfaz a relação dada.
-Cross ratios
Uma propriedade estreitamente relacionado de círculos envolve a geometria do cruzada proporção de pontos no plano complexo . Se A, B, e C são como acima, em seguida, o círculo de Apolônio para estes três pontos é o conjunto dos pontos P para o qual o valor absoluto da razão-cruzada é igual a um:
Dito de outra forma, P é um ponto na circunferência do Apolônio se e somente se o rácio de cruz [A, B, C, P] é a círculo unitário no plano complexo.
Círculos Generalizadas
Se C é a ponto médio do segmento AB, então o conjunto de pontos P satisfaz a condição Apolônio
não é um círculo, mas sim uma linha.
Assim, se A, B, e C são dadas pontos distintos no plano, em seguida, o lugar geométrico dos pontos P satisfaz a equação acima é chamado um "círculo generalizada." Ele pode ser um verdadeiro círculo ou uma linha. Neste sentido, uma linha é um círculo de raio infinito generalizada.
Círculos inscritos ou circunscritos sobre outras figuras
Em cada triângulo de um círculo original, chamado de circunferência inscrita, pode ser inscrito tal que é tangente a cada um dos três lados do triângulo.
Sobre cada triângulo de um círculo original, chamado de circunferência, pode ser circunscrito de tal modo que passa por cada um dos triângulo de três vértices.
Um polígono tangencial, tal como um quadrilátero tangencial, é qualquer polígono convexo dentro de um círculo que pode ser inscrito que é tangente a cada um dos lados do polígono.
A polígono cíclico é qualquer polígono convexo sobre o qual um círculo pode ser circunscrita, passando por cada vértice. Um exemplo bem estudado é a quadrilátero cíclico.
A hipociclóide é uma curva que se inscreve em um determinado círculo, traçando um ponto fixo em um círculo menor que rola dentro e tangente ao círculo dado.
Círculo como limitativos caso de outras figuras
O círculo pode ser visto como um caso limite de cada uma das várias outras figuras:
- A Oval cartesiano é um conjunto de pontos de tal forma que um soma ponderada das distâncias a partir de qualquer dos seus pontos de dois pontos fixos ( focos) é uma constante. Uma elipse é o caso em que os pesos são iguais. Um círculo é uma elipse com uma excentricidade igual a zero, o que significa que os dois focos coincidam uns com os outros, como o centro do círculo. Um círculo é também um caso especial diferente de uma oval cartesiano em que um dos pesos é zero.
- A super-elipse tem uma equação da forma
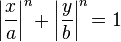 positivo para a, b, e n. Um supercircle tem b = a. Um círculo é o caso especial de um supercircle em que n = 2.
positivo para a, b, e n. Um supercircle tem b = a. Um círculo é o caso especial de um supercircle em que n = 2. - A Cassini oval é um conjunto de pontos tais que o produto das distâncias a partir de qualquer dos seus pontos para dois pontos fixos é uma constante. Quando os dois pontos fixos coincidem, um círculo resultados.
- A curva de largura constante, é uma figura cuja largura, definida como a distância perpendicular entre as duas linhas paralelas distintas cada intersecção do seu perímetro num único ponto, é a mesma independentemente da direcção destas duas linhas paralelas. O círculo é o exemplo mais simples deste tipo de figura.

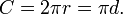
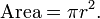
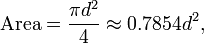
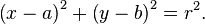
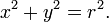
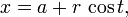
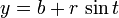
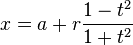
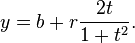
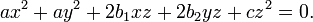
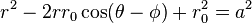
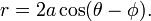
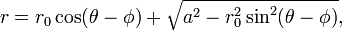
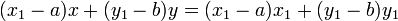
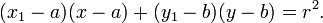
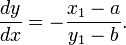
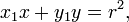
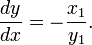
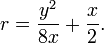
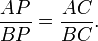
![| [A, B, C, P] | = 1. \](../../images/2039/203983.png)