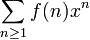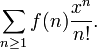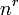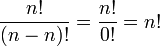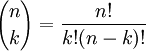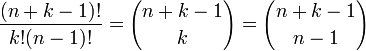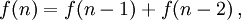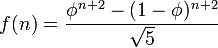Combinatória
Sobre este escolas selecção Wikipedia
Crianças SOS têm produzido uma seleção de artigos da Wikipedia para escolas desde 2005. Uma boa maneira de ajudar outras crianças é por patrocinar uma criança
Combinatória é um ramo da matemática pura relativas ao estudo de discretas (e geralmente finitos) objetos. Ela está relacionada com muitas outras áreas da matemática , tais como álgebra , teoria da probabilidade , teoria ergódica e geometria , bem como a assuntos aplicados em ciência da computação e física estatística. Aspectos da combinatória incluem "contar" os objetos que satisfazem determinados critérios ( combinatória enumerativa), decidindo quando os critérios podem ser satisfeitas, e construção e análise de objetos que satisfazem os critérios (como em modelos combinatórios e teoria matróide), encontrando "maior", "mais pequenos", ou objetos "ótimas" ( combinatória e extremais otimização combinatória), e encontrar algébricas estruturas desses objetos podem ter ( combinatória algébricas).
Combinatória é tanto sobre a resolução de problemas como a construção de teoria, embora tenha desenvolvido métodos teóricos poderosos, especialmente desde o final do século XX (ver página Lista de combinatória tópicos para obter detalhes sobre o desenvolvimento mais recente do assunto). Uma das partes mais antigas e mais acessíveis de análise combinatória é teoria dos grafos, que também tem inúmeras conexões naturais para outras áreas.
Existem muitos padrões combinatórios e teoremas relacionados com a estrutura dos conjuntos combinatoric. Estes muitas vezes se concentrar em um partição ou partição ordenada de um conjunto. Veja a Lista de tópicos de partição para uma lista expandida de tópicos relacionados ou o Lista de combinatória tópicos para uma lista mais geral. Alguns dos resultados mais notáveis são destacadas a seguir.
Um exemplo de uma pergunta combinatória simples é a seguinte: Qual é o número de possíveis ordenações de um baralho de 52 cartas de jogar distintas? A resposta é 52! (52 fatorial ), que é igual a cerca de 8,0658 x 10 67.
Outro exemplo de um problema mais difícil: Dado um determinado número n de pessoas, é possível atribuí-los a conjuntos de modo que cada pessoa é, em pelo menos um conjunto, cada par de pessoas é exatamente um jogo juntos, a cada dois conjuntos têm exatamente uma pessoa em comum, e nenhum conjunto contém todos, todos, mas uma pessoa, ou exatamente uma pessoa? A resposta depende de n. Consulte " teoria do projeto "abaixo.
Combinatória é usado com freqüência em ciência da computação para obter estimativas sobre o número de elementos de certos conjuntos. Um matemático que estuda combinatória é muitas vezes referida como um combinatorialist ou combinatorist.
História da Combinatória
Usos mais adiantados
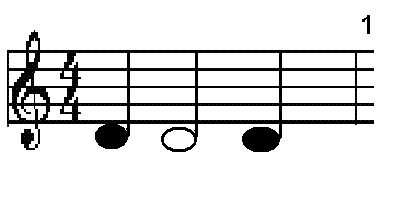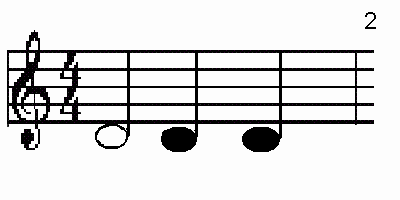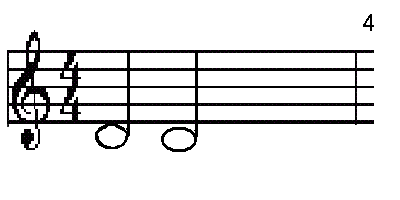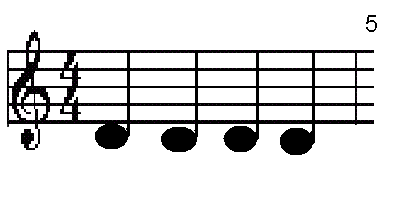
- Os primeiros livros sobre análise combinatória são da Índia. A Jainist texto, o Bhagabati Sutra, teve a primeira menção de um problema combinatória; ele perguntou quantas maneiras se poderia tomar seis sabores um, dois, ou três sabores de cada vez. O Bhagabati Sutra foi escrito por volta de 300 aC, e, portanto, foi o primeiro livro de mencionar a função de escolha . As próximas idéias de Combinatória veio de Pingala, que estava interessado em prosódia. Especificamente, ele queria saber quantas maneiras um medidor de seis sílaba pode ser feita a partir de notas curtas e longas. Ele escreveu este problema no sutra Chanda (também Chandahsutra) no segundo século antes de Cristo. Além disso, ele também encontrou o número de metros que tiveram notas n longas e breves notas k, o que é equivalente a encontrar os coeficientes binomial.
- As idéias do Bhagabati foram generalizados pelo matemático indiano Mahariva em 850 dC, ea obra de Pingala na prosódia foi ampliado por Bhaskara e Hemacandra em 1100 AD. Bhaskara foi a primeira pessoa conhecida para encontrar a função de escolha generalizada, embora Brahmagupta pode ter conhecido mais cedo. Hemacandra perguntou quantos metros existiu de um determinado período, se uma longa nota foi considerada duas vezes, enquanto uma nota curta, o que é equivalente a encontrar os números de Fibonacci.

- Enquanto a Índia foi o primeiro país a publicar os resultados em Combinatória, foram descobertas por outras nações sobre temas semelhantes. A primeira ligação conhecida para Combinatória vem do Rhind o papiro, problema 79, para a implementação de uma série geométrica. O próximo marco é mantido pelo I Ching . O livro é sobre o que diferentes hexagramas dizer, e para isso eles precisavam saber quantos hexagramas possível que houvesse. Uma vez que cada hexagrama é uma permutação com repetições de seis linhas, onde cada linha pode ser um dos dois estados, sólidos ou tracejadas, combinatória produz o resultado que os seus são
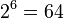 hexagramas. Um monge também pode ter contado o número de configurações para um jogo semelhante ao Vá ao redor de 700 AD. Embora a China teve relativamente poucos avanços na combinatória enumerativa, eles resolveram um problema de projeto combinatória, o quadrado mágico , em torno de 100 AD.
hexagramas. Um monge também pode ter contado o número de configurações para um jogo semelhante ao Vá ao redor de 700 AD. Embora a China teve relativamente poucos avanços na combinatória enumerativa, eles resolveram um problema de projeto combinatória, o quadrado mágico , em torno de 100 AD.
- Na Grécia, Plutarco escreveu que os Xenocrates descobriu o número de sílabas diferentes possíveis no idioma grego. Isso, no entanto, é pouco provável, porque esta é uma das poucas menções de Combinatória na Grécia. O número que encontraram,
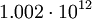 Também parece muito redonda a ser mais do que um palpite. .
Também parece muito redonda a ser mais do que um palpite. .
- Quadrados mágicos permaneceram um interesse da China, e eles começaram a generalizar o seu original é 3 × 3 quadrados entre 900 e 1300 dC. China correspondeu com o Oriente Médio sobre este problema no século 13. O Oriente Médio também aprendeu sobre coeficientes binomial de trabalho indiano, e encontrou a conexão com expansão polinomial.
Combinatória no Ocidente
- Combinatória chegou à Europa no século 13 através de dois matemáticos, Leonardo Fibonacci e Jordanus de Nemore. Fibonacci de Liber Abaci introduziu muitos do árabe e indiano ideias para a Europa, incluindo a dos números de Fibonacci. Jordanus foi a primeira pessoa para organizar o coeficiente binomial de em um triângulo, como fez na proposição 70 de De Arithmetica. Isso também foi feito no Oriente Médio em 1265, e da China por volta de 1300. Hoje, esse triângulo é conhecido como o triângulo de Pascal.
- A contribuição de Pascal ao triângulo que leva seu nome vem de seu trabalho em provas formais sobre o assunto, além de sua conexão entre ela e probabilidade. Juntamente com Leibniz e suas idéias sobre partições no século 17, eles são considerados os fundadores da combinatória modernos.
- Tanto Pascal e Leibniz entendeu que a álgebra e análise combinatória correspondeu (aka, a expansão binomial foi equivalente à função de escolha.) Este foi ampliado por De Moivre, que encontrou a expansão de um multinomial. De Moivre também encontrou a fórmula para desarranjos usando o princípio da inclusão-exclusão, um método diferente de Nikolaus Bernouli, que tinha encontrado-los previamente. Ele conseguiu aproximar o coeficientes binomial e fatorial. Finalmente, ele encontrou uma forma fechada para os números de Fibonacci inventando funções geradoras.
- No século 18, Euler trabalhou em problemas de análise combinatória. Além de trabalhar em vários problemas de probabilidade, que apontam para análise combinatória, ele trabalhou no cavaleiros tour, Quadrado greco-latina, Números de Euler, e outros. Ele também inventou a teoria dos grafos, resolvendo o Sete Pontes de problema Konigsberg, que também conduzem à formação de topologia . Finalmente, ele quebrou a terra com partições pelo uso de funções geradoras.
Combinatória enumerativa
Contando o número de maneiras que certos padrões podem ser formados é o problema central da combinatória enumerativa. Dois exemplos deste tipo de problema são combinações de contagem e contagem de permutações (como discutido na secção anterior). De modo mais geral, dado uma coleção infinita de conjuntos finitos S {i} indexados pelos números naturais , combinatória enumerativa procura descrever a função de contagem que conta o número de objetos em S n para cada n. Embora a contagem do número de elementos em um conjunto é um bastante amplo problema matemático, muitos dos problemas que surgem em aplicações têm uma descrição relativamente simples combinatória.
As mais simples são tais funções fórmulas fechadas, que podem ser expressas como uma composição de funções elementares tais como factoriais , poderes, e assim por diante. Por exemplo, como mostrado abaixo, o número de diferentes ordenamentos possíveis de um baralho de cartas n é f (n) = N!. Muitas vezes, não há forma fechada está inicialmente disponível. Nestes casos, frequentemente primeiro derivar uma relação de recorrência, em seguida resolver a recorrência para chegar à forma fechada desejado.
Finalmente, f (n) pode ser expressa por um série de potências formal, chamada de função geradora, que é mais vulgarmente ou o função geradora ordinária
ou o função geradora exponencial
Muitas vezes, uma fórmula fechada complicado produz pouco de conhecimento sobre o comportamento da função de contagem como o número de objetos contados cresce. Nestes casos, uma simples aproximação assintótica pode ser preferível. A função 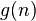 é uma aproximação assintótica para
é uma aproximação assintótica para 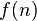 se
se 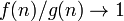 como
como 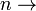 infinito . Neste caso, nós escrevemos
infinito . Neste caso, nós escrevemos 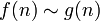 .
.
Uma vez determinada, a função geradora pode permitir que um para extrair toda a informação dada pelas abordagens anteriores. Além disso, as várias operações naturais na geração de funções tais como a adição, a multiplicação, diferenciação, etc., tem um significado combinatória; Isto permite que se estendem a partir de resultados de um problema combinatório de modo a resolver os outros.
Permutações com repetições
Quando a ordem de importância, e um objecto pode ser escolhido mais do que uma vez, o número de permutações é
onde n é o número de objetos a partir do qual você pode escolher e r é o número a ser escolhido.
Por exemplo, se você tem as letras A, B, C, e D e você deseja descobrir o número de maneiras de organizá-los em três padrões de letras ( trigramas)
- questões de ordem (por exemplo, AB é diferente de BA, ambos estão incluídos como possibilidades)
- um objecto pode ser escolhido mais do que uma vez (AA possível)
você descobrir que existem 3 ou 4 64 maneiras. Isto porque para o primeiro slot, você pode escolher qualquer um dos quatro valores, para o segundo slot, você pode escolher qualquer um dos quatro, e para a última vaga, você pode escolher qualquer uma das quatro letras. Multiplicando-los juntos dá o total.
Permutações sem repetições
Quando as questões de ordem e cada objecto pode ser escolhida apenas uma vez, em seguida, o número de permutações é
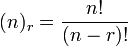 onde n é o número de objetos a partir do qual você pode escolher, r é o número a ser escolhido e "!" é o símbolo padrão significando fatorial .
onde n é o número de objetos a partir do qual você pode escolher, r é o número a ser escolhido e "!" é o símbolo padrão significando fatorial .
Por exemplo, se você tem cinco pessoas e vai escolher três entre estes, você terá 5 / (5-3)! = 60 permutações.
Note-se que se n = r (ou seja, o número de elementos escolhidos é igual ao número de elementos para escolher, cinco pessoas e escolher todos os cinco) torna-se então a fórmula
onde 0! = 1.
Por exemplo, se você tem as mesmas cinco pessoas e você quer descobrir quantas maneiras você pode organizá-los, seria 5! ou 5 × 4 × 3 × 2 × 1 = 120 maneiras. A razão para isso é que você pode escolher entre 5 para o slot inicial, então você é deixado com apenas 4 para escolher para o segundo slot etc. Multiplicando-los juntos dá o total de 120.
Combinações sem repetições
Quando a ordem não importa e cada objeto pode ser escolhida apenas uma vez, o número de combinações é o coeficiente binomial :
onde n é o número de objetos a partir do qual você pode escolher e K é o número a ser escolhido.
Por exemplo, se você tem dez números e deseja escolher 5 você teria 10 / (5 (10 -! 5))! = 252 maneiras de escolher. O coeficiente binomial também é utilizado para calcular o número de permutações numa lotaria.
As combinações com repetições
Quando a ordem não importa e um objeto pode ser escolhido mais de uma vez, em seguida, o número de combinações é
onde n é o número de objetos a partir do qual você pode escolher e K é o número a ser escolhido.
Por exemplo, se você tem dez tipos de rosquinhas (n) em um menu para escolher e você quer três anéis de espuma (k) não são (10 + 3-1)! / 3 (10 - 1)!! = 220 maneiras de escolher (ver também multiset).
Números de Fibonacci
Seja f (n) é o número de subconjuntos distintos do conjunto 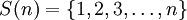 que não contêm dois números inteiros consecutivos. Quando n = 4, temos os conjuntos {}, {1}, {2}, {3}, {4}, {1,3}, {1,4}, {2,4}, de modo que f (4 ) = 8. Contamos os subconjuntos desejados de
que não contêm dois números inteiros consecutivos. Quando n = 4, temos os conjuntos {}, {1}, {2}, {3}, {4}, {1,3}, {1,4}, {2,4}, de modo que f (4 ) = 8. Contamos os subconjuntos desejados de 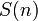 por contagem separadamente os subconjuntos que contêm elemento
por contagem separadamente os subconjuntos que contêm elemento 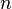 e aqueles que não o fazem. Se um subconjunto contém
e aqueles que não o fazem. Se um subconjunto contém 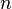 , Então ele não contém elemento
, Então ele não contém elemento 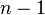 . Portanto, há exatamente
. Portanto, há exatamente 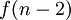 dos subconjuntos desejados que contêm elemento
dos subconjuntos desejados que contêm elemento 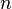 . O número de subconjuntos que não contêm
. O número de subconjuntos que não contêm 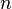 é simplesmente
é simplesmente 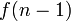 . A soma desses números juntos, temos a relação de recorrência:
. A soma desses números juntos, temos a relação de recorrência:
onde 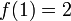 e
e 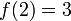 .
.
Tão cedo como 1202, Leonardo Fibonacci estudou esses números. Eles agora são chamados de números de Fibonacci ; em particular, 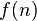 é conhecido como o
é conhecido como o 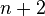 nd número de Fibonacci. Embora a relação de recorrência nos permite calcular todos os números de Fibonacci, o cálculo é ineficiente. No entanto, através da utilização de técnicas padrão para resolver relações de recorrência, que pode chegar a solução fechada:
nd número de Fibonacci. Embora a relação de recorrência nos permite calcular todos os números de Fibonacci, o cálculo é ineficiente. No entanto, através da utilização de técnicas padrão para resolver relações de recorrência, que pode chegar a solução fechada:
onde 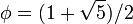 , A proporção áurea .
, A proporção áurea .
No exemplo acima, uma aproximação para assintótica 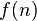 é:
é:
como n se torna grande.
Combinatória estruturais
A teoria dos grafos
Os gráficos são objetos básicos de análise combinatória. As perguntas variam de contagem (por exemplo, o número de gráficos em n vértices com k arestas) para estrutural (por exemplo, que contenham gráficos Ciclos hamiltonianos).
Teoria do design
Um resultado simples no a área de criação de blocos de combinatória é que o problema de conjuntos que formam, descrito na introdução, tem uma solução única, se n tem a forma q 2 + q + 1. É menos simples para provar que uma solução se existe q é um potência primária. Conjectura-se que estas são as únicas soluções. Foi ainda demonstrado que, se existe uma solução para q congruente com 1 ou 2 mod 4, Q é uma soma de dois números de quadrados. Este último resultado, o Bruck-Ryser teorema, é provada por uma combinação de métodos construtivos baseados em campos de finitos e um pedido de formas quadráticas.
Quando tal estrutura existir, ele é chamado de um finito plano projetivo; evidenciando o quão geometria finita e análise combinatória cruzam.
Teoria matróide
Teoria matróide abstrai parte da geometria . Ele estuda as propriedades de conjuntos (geralmente, conjuntos finitos) de vetores em um espaço vetorial que não dependem dos coeficientes específicos em um relação de dependência linear. Não só a estrutura, mas também propriedades enumerativos pertencem a matróide teoria.
Por exemplo, dado um conjunto de n vetores no espaço euclidiano , o que é o maior número de aviões que pode gerar? Resposta: o coeficiente binomial
Existe um conjunto que gera exatamente um a menos avião? (Não, em quase todos os casos.) Estas são questões extremas em geometria, como discutido abaixo.
Extremal e combinatória probabilísticos
Muitas perguntas extremais lidar com Conjunto sistemas. Um exemplo simples é o seguinte: o que é o maior número de subconjuntos de um n -element definir um pode ter, se nenhum dos dois subconjuntos são disjuntos? Resposta: metade do número total de subconjuntos. Prova: Chame o n set -element S. Entre qualquer subconjunto T e a sua complementar S - T, no máximo, um pode ser escolhido. Isto prova o número máximo de subconjuntos escolhidos não é maior do que metade do número de subconjuntos. Para mostrar a pessoa pode alcançar a metade do número, escolher um elemento x de S e escolher todos os subconjuntos que contenham x.
Um problema mais difícil é caracterizar as soluções extremas; neste caso, para mostrar que nenhuma outra escolha de subconjuntos pode atingir o número máximo, desde que satisfaçam a exigência.
Muitas vezes é muito difícil até mesmo para encontrar a resposta extremal f (n) exatamente e só se pode dar um estimativa assintótica.
Teoria de Ramsey
Teoria de Ramsey é uma parte célebre de combinatória extremal. Ele afirma que qualquer suficientemente configuração aleatória grande conterá algum tipo de ordem.
Frank P. Ramsey mostrou que para cada número inteiro k não é um número inteiro n, de tal modo que cada gráfico em n vértices ou contém um clique ou um conjunto independente de tamanho k. Este é um caso especial de Teorema de Ramsey. Por exemplo, dado um grupo de seis pessoas, é sempre o caso que se pode encontrar três pessoas fora desse grupo que quer todos conhecem uns aos outros ou todos não se conhecem. A chave para a prova, neste caso, é a Princípio Pigeonhole: ou A sabe três dos restantes pessoas, ou A não sabe três dos restantes pessoas.
Aqui está uma prova simples: Pegue qualquer uma das seis pessoas, chamá-lo de A. De qualquer Um conhece três dos restantes pessoas, ou A não sabe três dos restantes pessoas. Suponha que o primeiro (a prova é idêntica se assumirmos o último). Deixe que as três pessoas que sabe ser um B, C, e D. Agora, ou duas pessoas de {B, C, D} conhecer uns aos outros (caso em que temos um grupo de três pessoas que se conhecem - estes dois, mais um ) ou nenhum dos B, C, D conhecer uns aos outros (caso em que temos um grupo de três pessoas que não se conhecem - B, C, D). QED.
Combinatória extremal
Os tipos de questões abordadas neste caso está prestes a maior gráfico possível que satisfaz certas propriedades. Por exemplo, o maior gráfico livre de triângulo nos vértices 2n é uma grafo completo bipartido K n, n.
Combinatória probabilísticos
Aqui as questões são do seguinte tipo: qual é a probabilidade de uma determinada propriedade gráfica para um gráfico aleatório (dentro de uma determinada classe) Por exemplo, qual é o número médio de triângulos em um gráfico aleatório?
Combinatória geométricas
Combinatória geométrica está relacionada com convexo e geometria discreta. Ele pede, por exemplo, quantas faces de cada dimensão pode um polytope convexas têm. Propriedades métricas de polytopes desempenhar um papel importante, bem como, por exemplo, o Cauchy teorema sobre rigidez de policações convexas. Polytopes especiais também são considerados, tais como permutohedron, e associahedron Birkhoff polytope.