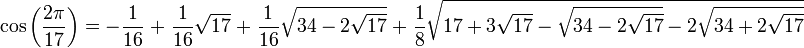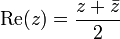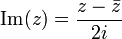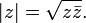Régua e compasso construções

A criação de um hexágono regular com uma régua e compasso

Construção de um pentágono regular

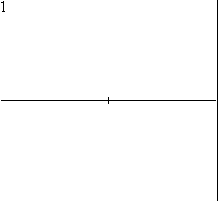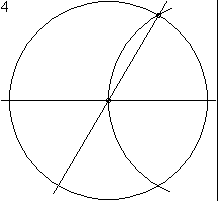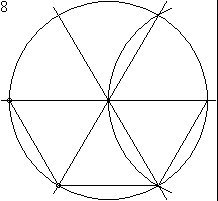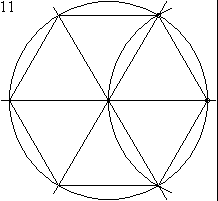
Compass-e-régua ou construção governante-e-compass é a construção de comprimentos, ângulos e outras figuras geométricas usando apenas um idealizada régua e bússola.

A régua idealizada, conhecido como um régua, é assumido como sendo infinita de comprimento, e não tem marcações sobre ele e apenas uma borda. O compasso é assumido a entrar em colapso quando levantada a partir da página, de modo que não pode ser utilizado directamente para transferir distâncias. (Esta é uma limitação importante, como isto pode ser conseguido através da teorema de equivalência bússola.) Mais formalmente, as únicas construções permitidas são as atribuídas por Euclides três primeiros postulados 's.

Cada constructible ponto usando régua e compasso podem ser construídas usando bússola sozinho. Uma série de problemas antigos em geometria plana impor esta restrição.

Os mais famosos problemas straightedge-e-compass ter sido provada impossível em vários casos, por Pierre Wantzel, utilizando a matemática teoria dos campos. Apesar de provas existentes de impossibilidade, alguns persistência na tentativa de resolver esses problemas. Muitos desses problemas são facilmente solucionáveis, desde que outras transformações geométricas são permitidos: por exemplo, duplicação do cubo é possível usando construções geométricas, mas não é possível usando régua e compasso sozinho.

Matemático Underwood Dudley fez uma linha de recolha de provas falsas governante-e-bússola, bem como outros trabalhos de matemática manivelas, e recolheu-os em vários livros.

Ferramentas régua e compasso

Uma bússola

Os "bússola" e "régua" de régua e compasso construções são idealizações de governantes e bússolas do mundo real:

• A bússola pode ser aberto arbitrariamente grande, mas (ao contrário de alguns real bússolas) não tem marcações sobre ele. Círculos só pode ser desenhado com dois pontos existentes que dão o centro e um ponto na circunferência. A bússola colapsa quando não é usado para o desenho, não pode ser usado para copiar um comprimento para outro lugar.
• A régua é infinitamente longo, mas não tem marcações sobre ele e tem apenas uma borda, ao contrário governantes comuns. Ela só pode ser usada para desenhar um segmento de linha entre dois pontos ou estender uma linha existente.

A bússola moderna geralmente não entrar em colapso e várias construções modernas usar esse recurso. Parece que a bússola moderna é um instrumento "mais poderoso" do que o compasso antigo. No entanto, pela Proposição 2 do Livro 1 de Elementos de Euclides , nenhum poder computacional está perdido usando essa bússola em colapso; não há necessidade de transferência de uma distância a partir de um local para outro. Embora a proposição é correta, suas provas têm uma história longa e variada.

Cada construção deve ser exata. "Eyeballing" ele (essencialmente olhando para a construção e adivinhando a sua precisão, ou usando alguma forma de medição, tais como as unidades de medida em uma régua) e chegando perto não conta como uma solução.

Cada construção deve terminar. Ou seja, ele deve ter um número finito de passos, e não ser o limite de aproximações cada vez mais estreitos.

Afirmou Desta forma, régua e compasso construções parecem ser um jogo de salão, ao invés de um problema prático sério; mas o objetivo da restrição é garantir que as construções podem ser provado ser exatamente correto, e é, portanto, importante tanto para a elaboração (concepção por ambos Software CAD e elaboração tradicional com lápis, papel, straight-edge e bússola) ea ciência de pesos e medidas, nas quais a síntese exata de corpos, ou materiais de referência é extremamente importante. Um dos principais efeitos da matemática grega era encontrar construções exatas para vários comprimentos; por exemplo, o lado de um pentágono inscrito num determinado círculo. Os gregos não poderiam encontrar construções para três problemas:

• Quadratura do círculo: Desenhando um quadrado na mesma área que um círculo dado.
• Duplicação do cubo: Desenhando um cubo com o dobro do volume de um determinado cubo.
• Triseccionar o ângulo: Dividir um determinado ângulo em três ângulos menores todas do mesmo tamanho.

Durante 2000 anos as pessoas tentaram encontrar construções dentro dos limites fixados acima, e falharam. Todos os três foram agora testados sob regras matemáticas para ser impossível geral (ângulos com certos valores pode ser trisected, mas não todos os ângulos possíveis).

As construções básicas

As construções básicas

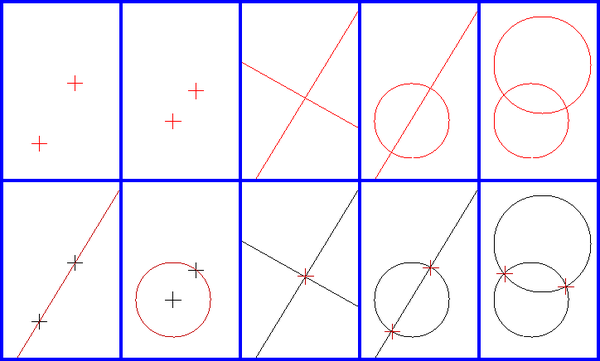
Todos os régua e compasso construções consistem em aplicação repetida de cinco construções básicas usando os pontos, linhas e círculos que já foram construídas. Estes são:

• Criando a linha através de dois pontos existentes

• Criando o círculo através de um ponto com o centro de outro ponto

• Criando o ponto que é a interseção de duas linhas existentes, não paralelos

• Criação de um ou dois pontos na intersecção de uma linha e um círculo (se eles se cruzam)

• Criação de um ou dois pontos na interseção de dois círculos (se eles se cruzam).

Por exemplo, começando com apenas dois pontos distintos, que pode criar uma linha ou qualquer um de dois círculos (Por sua vez, a utilização de cada ponto de centro e que passa através do outro ponto). Se traçarmos ambos os círculos, dois novos pontos são criados em suas interseções. Linhas do desenho entre os dois pontos originais e um desses novos pontos de concluir a construção de um triângulo equilátero.

Portanto, em qualquer problema geométrico que temos um conjunto inicial de símbolos (pontos e linhas), um algoritmo, e alguns resultados. A partir desta perspectiva, a geometria é equivalente a uma axiomática álgebra , substituindo seus elementos por símbolos. Provavelmente Gauss primeiro percebeu isso, e é usado para provar a impossibilidade de algumas construções; Só muito mais tarde Hilbert encontrar um conjunto completo de axiomas para a geometria.

Pontos constructible e comprimentos

Triseccionar um segmento com régua e compasso.

A prova formal

Há muitas maneiras diferentes para provar alguma coisa é impossível. A prova mais rigorosa seria para demarcar o limite do possível, e mostram que, para resolver estes problemas deve-se transgredir que limite. Muito do que pode ser construído está coberto de teoria interceptação.

Nós poderíamos associar uma álgebra para a nossa geometria usando um sistema de coordenadas cartesianas, feito de duas linhas, e representam pontos de nosso avião por vetores. Finalmente, podemos escrever esses vetores como números complexos.

Utilizando as equações para linhas e círculos, pode-se mostrar que os pontos em que se cruzam num mentira extensão menor quadrática do campo F contendo dois pontos sobre a linha, o centro do círculo, e o raio do círculo. Isto é, elas são da forma 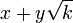, Em que x, y, e k são em F.

Uma vez que o campo de pontos constructible é fechada sob a raiz quadrada, que contém todos os pontos que podem ser obtidos por uma sequência finita de extensões quadráticas do campo de números complexos com coeficientes racionais. Com o parágrafo anterior, pode-se mostrar que qualquer ponto construtıvel pode ser obtido por uma tal sequência de extensões. Como corolário disso, verifica-se que o grau do polinômio mínimo para um ponto (e, portanto, de qualquer comprimento constructible) constructible é uma potência de 2. Em particular, qualquer ponto constructible (ou comprimento) é uma número algébrico, embora nem todos os números algébricos é constructible (ou seja, a relação entre o comprimento dos constructible e números algébricos não é bijective); por exemplo, é algébrica, mas não constructible.

Ângulos construtível

Existe um bijection entre os ângulos que são constructible e os pontos que são constructible em qualquer círculo constructible. Os ângulos que são uma forma constructible grupo abeliano sob adição módulo 2π (o que corresponde a multiplicação dos pontos sobre o círculo unitário vistos como números complexos). Os ângulos que são constructible são exatamente aqueles cuja tangente (ou equivalentemente, seno ou co-seno) é constructible como um número. Por exemplo o normal heptadecagon é porque constructible

como descoberto por Gauss .

O grupo de ângulos constructible é fechada sob a operação que as metades ângulos (o que corresponde a tomar raízes quadradas). As únicas ângulos de ordem finita que podem ser construídas a partir de dois pontos são aqueles cuja sequência é uma potência de dois, ou um produto de uma potência de dois e um conjunto de distinto Fermat primos. Além disso, há um conjunto denso de ângulos constructible de ordem infinita.

Régua e compasso construções como aritmética complexa

Dado um conjunto de pontos no plano euclidiano , a seleção de qualquer um deles para ser chamado 0 e outra para ser chamado 1, juntamente com uma escolha arbitrária de Orientação permite-nos considerar os pontos como um conjunto de números complexos .

Como números complexos dado qualquer interpretação de um conjunto de pontos, os pontos constructible usando régua e compasso construções válidas por si só são precisamente os elementos do menor campo que contém o conjunto original de pontos e fechou sob a conjugado e complexos raiz quadrada operações (para evitar ambigüidade, podemos especificar a raiz quadrada com argumento complexa inferior a π). Os elementos deste campo são precisamente aqueles que podem ser expressas como uma fórmula nos pontos originais usando apenas as operações de adição , subtração , multiplicação , divisão , complexo conjugado, e a raiz quadrada , que é facilmente visto ser um subconjunto denso contáveis do avião. Cada um destes seis operações correspondentes a um compasso simples e construção régua. A partir de uma tal fórmula é muito simples para produzir uma construção de ponto correspondente ao combinar as construções para cada uma das operações aritméticas. Construções mais eficientes de um determinado conjunto de pontos correspondem a atalhos em tais cálculos.

Equivalentemente (e sem a necessidade de escolher arbitrariamente dois pontos), podemos dizer que, dada uma escolha arbitrária de orientação, um conjunto de pontos determina um conjunto de relações complexas dadas pelas razões das diferenças entre quaisquer dois pares de pontos. O conjunto de rácios construtível usando régua e compasso de um conjunto de tais proporções é precisamente o menor campo que contém os índices originais e fechado sob tomando conjugados complexos e raízes quadradas.

Por exemplo, a parte real e a parte imaginária de um módulo de ponto ou a razão de z (tendo um dos dois pontos de vista acima referidos) são construtıvel vez que estes podem ser expressos como

Duplicação do cubo e trissecção de um ângulo (com exceção de ângulos especiais, como qualquer φ tal que φ / 6π é um número racional com denominador o produto de uma potência de dois e um conjunto de distintos Primos de Fermat) exigem rácios que são a solução para equações cúbicos, enquanto a quadratura do círculo requer um relação transcendental. Nenhum destes são nas áreas descritas, portanto, nenhuma régua e compasso de construção para estes existe.

Construções impossíveis

Os três problemas de construção seguintes, cujas origens datam da antiguidade grega, eram consideradas impossíveis no sentido de que eles não poderiam ser resolvidos usando apenas a régua e compasso. Com métodos matemáticos modernos, esta "consideração" dos matemáticos gregos pode ser provou ser correta. Os próprios problemas, no entanto, são factíveis, e os gregos sabiam como resolvê-los, sem a restrição de trabalhar apenas com régua e compasso.

Quadratura do círculo

O mais famoso desses problemas, quadratura do círculo, também conhecida como a quadratura do círculo, envolve a construção de um quadrado com a mesma área que um círculo dado usando apenas régua e compasso.

Quadratura do círculo foi provado impossível, uma vez que envolve a geração de um número transcendental, isto é, 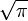. Apenas certa números algébricos podem ser construídos com régua e compasso sozinho, ou seja, aqueles construídos a partir dos números inteiros com uma sequência finita de operações de adição, subtração, multiplicação, divisão, e tendo raízes quadradas. A frase "quadratura do círculo" é muitas vezes usado para significar "fazer o impossível" por este motivo.

Sem a restrição de que exige solução por régua e bússola sozinho, o problema é facilmente solúvel por uma ampla variedade de médias geométricas e algébricas, e foi resolvido muitas vezes na antiguidade.

Duplicação do cubo

Duplicação do cubo: usando apenas uma régua e compasso, construir o lado de um cubo que tem o dobro do volume de um cubo com um determinado lado. Isso é impossível, porque a raiz cúbica de 2, embora algébrica, não pode ser calculado a partir inteiros por adição, subtração, multiplicação, divisão, e tendo raízes quadradas. Isto segue porque o seu polinomial mínima sobre os racionais tem grau 3. Essa construção é possível usando uma régua com duas marcas nele e uma bússola.

Trissecção ângulo

Trisecção Ângulo: utilizando apenas uma régua e um compasso, construir um ângulo que é um terço de um determinado ângulo arbitrário. Esta é impossível no caso geral. Por exemplo: se o ângulo de π / 3 radianos (60 ° ) não pode ser trisected, o ângulo 2π / 5 radianos (72 ° = 360 ° / 5) pode ser trisected. Este problema também é facilmente resolvido quando uma régua com duas marcas no que é permitido (a construção neusis).

A construção de polígonos regulares

Construção de uma praça.

Alguns polígonos regulares (por exemplo, uma pentágono) são fáceis de construir com régua e compasso; outros não são. Isto levou à pergunta: É possível construir todos os polígonos regulares com esquadro e compasso?

Carl Friedrich Gauss em 1796 mostrou que a n regulares -sided polígono pode ser construído com esquadro e compasso se o estranho fatores primos de n são distintos Fermat primos. Gauss conjecturou que esta condição também foi necessário, mas ele não ofereceu nenhuma prova desse fato, que foi fornecida por Pierre Wantzel em 1837.

Construindo com apenas régua ou única bússola

É possível (de acordo com o Mohr-Mascheroni teorema) para construir qualquer coisa com apenas uma bússola se ele pode ser construído com uma régua e compasso, desde que os dados fornecidos e os dados a serem encontrados consistem em pontos discretos (não linhas ou círculos). É impossível tomar uma raiz quadrada com apenas uma régua, então algumas coisas que não podem ser construídos com uma régua pode ser construído com uma bússola; mas (pela Poncelet-Steiner teorema) dado um único círculo e seu centro, que pode ser construída.

Construções prolongadas

Governantes marcantes

Archimedes e Apolônio deu construções que envolvem o uso de uma régua markable. Isto iria permitir-lhes, por exemplo, tomar um segmento de linha, duas linhas (ou círculos), e um ponto; e, em seguida, desenhar uma linha que passa através do ponto de dado e intersecta ambas as linhas, e de tal modo que a distância entre os pontos de intersecção é igual ao segmento de dados. Isto os gregos chamavam neusis ("inclinação", "tendência" ou "beirando"), porque a nova linha tende ao ponto. Neste esquema expandido, qualquer distância cuja relação a uma distância existente é a solução de um cúbico ou um equação quártica é constructible. Daqui resulta que, se são permitidas governantes marcantes e neusis, o trissecção do ângulo (ver Arquimedes trissecção) ea duplicação do cubo pode ser alcançado; a quadratura do círculo é ainda impossível. Alguns polígonos regulares, como o heptagon, tornar-se constructible; e John H. Conway dá construções para várias delas; mas o polígono de 11 lados, o hendecágono, ainda é impossível, e infinitamente muitos outros.

Quando apenas um trisector ângulo é permitida, há uma descrição completa de todos os polígonos regulares que podem ser construídos, incluindo acima mencionado regulares heptagon, triskaidecagon (13-gon) e enneadecagon (19-gon). Está aberto se existem infinitos números primos p para o qual um Gon p regular é constructible com régua, compasso e um trisector ângulo.

Origami

O teoria matemática do origami é mais poderoso do compasso e construção staightedge. Dobras satisfazendo os axiomas Huzita-Hatori pode construir exatamente o mesmo conjunto de pontos como as construções estendidos usando uma bússola e uma régua marcada. Portanto origami também pode ser utilizado para resolver equações cúbicos (e, portanto, equações quartic), e, portanto, resolver os problemas de dois clássicos.

O campo de extensão

Em termos abstratos, o uso dessas ferramentas mais poderosas de qualquer neusis usando uma régua markable ou as construções de origami estende-se no campo de números constructible a um subcampo maior dos números complexos, que contém não só a raiz quadrada, mas também a cubo raízes, de cada elemento. As fórmulas aritméticas para pontos constructible descritas acima têm analogias neste domínio maior, permitindo fórmulas que incluem raízes cúbicas bem. A extensão do campo gerado por qualquer constructible ponto adicional nesta área maior tem grau um múltiplo de uma potência de dois e um poder de três, e pode ser dividido em uma torre de extensões de grau 2 e 3.

Computação de dígitos binários

Em 1998 Simon Plouffe deu régua e compasso algoritmo que pode ser usado para computar dígitos binários de certos números. O algoritmo envolve basicamente a duplicação repetida de um ângulo e torna-se impraticável fisicamente após cerca de 20 dígitos binários.