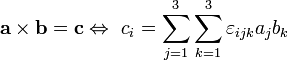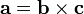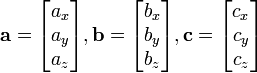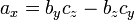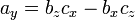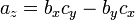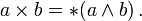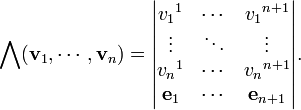Produto cruzado
Informações de fundo
Esta seleção é feita para as escolas de caridade infantil leia mais . Com SOS Children você pode escolher para patrocinar crianças em mais de cem países
Em matemática , o produto cruzado é um operação binária em dois vectores em um tridimensional espaço euclidiano que resulta num outro vector que seja perpendicular aos dois vectores de entrada. Em contraste, o produz um produto de ponto resultado escalar. Em muitos problemas de engenharia e física, é muito útil ser capaz de construir um vector perpendicular a partir de dois vectores existentes, e o produto transversal fornece um meio para o fazer. O produto cruzado é também conhecido como o produto do vetor, ou Gibbs produto do vetor.
O produto cruzado não é definido excepto em três dimensões (eo álgebra definida pelo produto cruz não é associativa ). Como o produto de ponto, isso depende do métrica do espaço euclidiano. Ao contrário do produto de pontos, também depende da escolha de orientação ou "imparcialidade". Certas características do produto cruzado pode ser generalizada a outras situações. Para escolhas arbitrárias de orientação, o produto cruzado não deve ser considerada como um vector, mas como um pseudovetor. Para escolhas arbitrárias de métrica, e em dimensões arbitrárias, o produto cruzado pode ser generalizada pela produto exterior de vectores, que define uma de dois em vez de uma forma de vector.
Definição
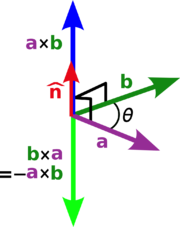
O produto cruzado de dois vectores de a e b é denotado por um × b. Em um tridimensional espaço euclidiano , com um costume sistema de coordenadas destro , ele é definido como um vetor c que é perpendicular tanto a e b, com uma orientação dada pela regra da mão direita e uma amplitude igual à área do paralelogramo que os vetores abrangem.
O produto cruzado é dada pela fórmula
onde θ é a medida do ângulo entre a e b (0 ° ≤ θ ≤ 180 °), a e b são as magnitudes dos vectores de a e b, e 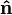 é um unidade vetor perpendicular ao plano que contém a e b. Se a vectores de a e b são colineares (isto é, o ângulo entre elas é θ ou 0 ° ou 180 °), pela fórmula acima, o produto cruzado de a e b é zero, o vector de 0.
é um unidade vetor perpendicular ao plano que contém a e b. Se a vectores de a e b são colineares (isto é, o ângulo entre elas é θ ou 0 ° ou 180 °), pela fórmula acima, o produto cruzado de a e b é zero, o vector de 0.
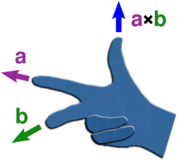
A direcção do vector 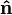 é dado pela regra da mão direita, onde se observa simplesmente o dedo indicador da mão direita no sentido de um e o dedo médio na direcção de b. Em seguida, o vector
é dado pela regra da mão direita, onde se observa simplesmente o dedo indicador da mão direita no sentido de um e o dedo médio na direcção de b. Em seguida, o vector  está saindo do polegar (veja a imagem à direita).
está saindo do polegar (veja a imagem à direita).
Usando o produto cruzado requer a destreza manual do sistema de coordenadas a ser tomado em conta (tal como explicitado na definição acima). Se um sistema de coordenadas canhoto é usado, a direcção do vector  é dado pela regra da mão esquerda e aponta na direcção oposta.
é dado pela regra da mão esquerda e aponta na direcção oposta.
Isso, no entanto, cria um problema, porque a transformação de um sistema de referência arbitrária para outro (por exemplo, uma transformação de imagem espelho de um destro para um sistema de coordenadas da mão esquerda), não devem mudar a direção do  . O problema é clarificado por perceber que o produto cruzado de dois vectores não é um (verdadeiro) vector, mas sim um pseudovetor. Veja produto cruzado e destreza manual para mais detalhes.
. O problema é clarificado por perceber que o produto cruzado de dois vectores não é um (verdadeiro) vector, mas sim um pseudovetor. Veja produto cruzado e destreza manual para mais detalhes.
Calculando o produto cruzado
Coordenar notação
O vectores unitários i, j e k a partir do sistema de coordenadas ortogonal dada satisfazer as seguintes desigualdades:
- i × j = k × k = j i k × i = j.
Com estas regras, as coordenadas do produto cruzado de dois vetores pode ser calculada facilmente, sem a necessidade de determinar quaisquer ângulos: Deixe-
- A = A 1 um i + j + 2 um k = 3 (a 1, A 2, A 3)
e
- b = b 1 i + j + b 2 b 3 k = (b 1, b 2, 3 b)
Em seguida
- a × b = (a 2 b 3 - a 3 b 2) i + (a 3 b 1 - a 1 b 3) j + (a 1 b 2 - a 2 b 1) k = (a 2 b 3 - a 3 b 2, uma 3 1 b - b 3 1 um, um 1 b 2 - a 2 b 1)
Notação matricial
A notação de coordenadas também pode ser escrita formalmente como o determinante de uma matriz :
O determinante de três vectores podem ser recuperados como
- det (a, b, c) = a · (b × c).
Intuitivamente, o produto cruzado pode ser descrito pela Sarrus esquema '. Considere a mesa
Para os três primeiros vetores unitários, multiplique os elementos na diagonal para a direita (por exemplo, a primeira diagonal conteria i, a 2, e b 3). Para os últimos três vectores unitários, multiplicar os elementos na diagonal para a esquerda e, em seguida, negar o produto (por exemplo, o último diagonal conteria k, um 2, e b 1). O produto transversal seria definida pela soma destes produtos:
Embora escrito aqui em termos de coordenadas, segue-se a partir da definição geométrica acima que o produto cruzado é invariante sob rotações em torno do eixo definido por um × b, e vira sinal sob trocando a e b.
Exemplos
Exemplo 1
Considere dois vectores, a = (1,2,3) e b = (4,5,6). O produto de um cruzamento × b é
- um × b = (1,2,3) x (4,5,6) = ((2 × 6-3 × 5), - (1 × 6-3 × 4), + (1 × 5 - 2 × 4)) = (-3,6, -3).
Exemplo 2
Considere dois vetores, a = (3,0,0) e b = (0,2,0). O produto de um cruzamento × b é
- a × b = (3,0,0) x (0,2,0) = ((0 × 0-0 × 2), (0 × 0-3 × 0), (3 × 2-0 × 0) ) = (0,0,6).
Este exemplo tem os seguintes interpretações:
- A área do paralelogramo (um rectângulo, neste caso) é 2 × 3 = 6.
- O produto cruzado de quaisquer dois vectores no plano xy será paralela ao eixo z.
- Uma vez que a componente z do resultado for positivo, o ângulo obtuso não a partir de um para b é anti-horário (quando observada de um ponto sobre os semiaxis + Z, e quando o sistema de coordenadas é destro).
Propriedades
Significado geométrico
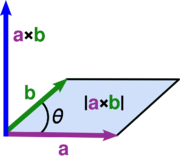
A magnitude do produto cruzado pode ser interpretado como o unsigned área do paralelogramo que tem a e b como os lados:
Com efeito, pode-se também calcular o volume V do tendo um paralelepípedo, b e c como os lados, utilizando uma combinação de um produto de cruzamento e um produto de pontos, chamados escalar produto triplo:
Propriedades algébricas
O produto vetorial é anticomutativa,
- a × b = - b × uma,
distributivos sobre adição,
- um × (b + c) = (a x b) + (c uma ×),
e compatível com a multiplicação escalar de modo que
- (Ra) × b = a x (R b) = r (um × b).
Não é associativo , mas satisfaz a Jacobi identidade:
- a × (b × c) + b × (c × a) + c × (a × b) = 0.
Ele não obedece à Direito de cancelamento:
- Se a × b = a × c e uma ≠ 0, então podemos escrever:
- (Um × b) - (c uma ×) = 0 e, pela lei de distribuição acima:
- um × (b - c) = 0
- Agora, se uma é paralela à (b - c), então mesmo se uma ≠ 0, é possível que (b - c) ≠ 0 e, por conseguinte, que b ≠ c.
No entanto, se ambos a · b = a · c e a × b = a × c, então podemos concluir que b = c. Com efeito,
- um. (B - c) = 0, e
- um × (b - c) = 0
de modo a que b - c é tanto paralela e perpendicular ao vector diferente de zero um. Isso só é possível se b - c = 0.
A distributividade, linearidade e Jacobi mostra identidade que R 3, juntamente com a adição de vetores e produto forma uma cruz Deite álgebra.
Além disso, dois vectores diferentes de zero a e b são paralelas sse a × b = 0.
Expansão do produto Triplo
A expansão do produto tripla, também conhecida como fórmula de Lagrange, é uma fórmula que relaciona o produto cruzado de três vectores (chamado o produto triplo vector) com o produto escalar:
- a × (b × c) = b (a · c) - c (a · b).
O "ONT menos CAB" mnemônico é usado para lembrar a ordem dos vetores no membro mão direita. Esta fórmula é utilizada na física para simplificar os cálculos de vectores. Um caso especial, sobre gradientes e útil no cálculo vetorial , é dado abaixo.
Este é um caso especial da mais generalizada LAPLACIANO-de Rham 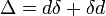 .
.
A identidade seguinte refere-se também o produto cruzado e produto escalar:
Este é um caso especial do multiplicatividade 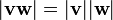 da norma no álgebra quaternion, e que uma restrição
da norma no álgebra quaternion, e que uma restrição 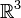 de A identidade de Lagrange.
de A identidade de Lagrange.
Formas alternativas de calcular o produto cruzado
Quaternions
O produto transversal também pode ser descrita em termos de quaternions, e é por isso que as letras i, j, k são uma convenção para a base padrão em 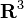 : Ele está sendo pensado como os quaternions imaginários.
: Ele está sendo pensado como os quaternions imaginários.
Aviso por exemplo, que os produtos acima dadas as relações cruzadas entre i, j, k e concordar com as relações multiplicativas entre os quaternions i, j, k. Em geral, se representar um vector [a 1, A 2, A 3] como o quatérnion uma 1 i + j + a 2 a 3 K, obtém-se o produto cruzado de dois vectores, tendo os seus produtos como quatérnions e a exclusão do parte real do resultado. A parte real será o negativo da produto escalar dos dois vectores.
Conversão para multiplicação de matrizes
Um produto de cruzamento entre dois vectores (que só pode ser definido no espaço tridimensional) pode ser reescrita em termos de multiplicação de matrizes puro como o produto de um distorcer-matriz simétrica e um vector, como se segue:
onde
Além disso, se 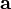 é em si um produto cruzado:
é em si um produto cruzado:
em seguida
Esta notação fornece uma outra maneira de generalizar produto cruzado para as dimensões superiores substituindo pseudovectors (tais como a velocidade angular ou campo magnético) com matrizes tais inclinar-simétrica. É claro que tais quantidades físicas terá n (n-1) / 2 componentes independentes em n dimensões, o que coincide com o número de dimensões para o espaço tridimensional, e é por isso que os vectores podem ser utilizados (e na maioria das vezes são usados) para representar tais quantidades.
Esta notação é também muitas vezes muito mais fácil de trabalhar com, por exemplo, em geometria epipolar.
Entre as propriedades gerais do produto transversal que segue imediatamente
![[\ Mathbf {a}] _ {} \ times \, \ mathbf {a} = \ mathbf {0}](../../images/212/21241.png) e
e ![\ Mathbf {a} ^ {T} \, [\ mathbf {a}] _ {\ times} = \ mathbf {0}](../../images/212/21242.png)
e de facto ![[\ Mathbf {a}] _ {} \ times](../../images/212/21243.png) é enviesado-simétrica que resulta
é enviesado-simétrica que resulta
A expansão do produto triplo supramencionado (regra bac-táxi) pode ser facilmente comprovada utilizando esta notação.
A definição acima de ![[\ Mathbf {a}] _ {} \ times](../../images/212/21243.png) significa que existe um mapeamento um-para-um entre o conjunto de matrizes 3 × 3 inclinação-simétricos, também denotado SO (3), e a operação de levar o produto cruzado com algum vetor
significa que existe um mapeamento um-para-um entre o conjunto de matrizes 3 × 3 inclinação-simétricos, também denotado SO (3), e a operação de levar o produto cruzado com algum vetor 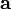 .
.
Notação Index
O produto transversal pode, alternativamente, ser definido em termos da Levi-Civita tensor 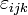
onde os índices 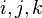 correspondem, como na seção anterior, a componentes de vetores ortogonais.
correspondem, como na seção anterior, a componentes de vetores ortogonais.
Mnemônico
A palavra xyzzy pode ser usado para lembrar a definição do produto cruzado.
Se
onde:
em seguida:
Note-se que a segunda e terceira equações pode ser obtido a partir do primeiro verticalmente, bastando rodar os subscritos, x → y z → → x. O problema, naturalmente, é como me lembro da primeira equação, e duas opções estão disponíveis para este propósito: ou você se lembrar das duas diagonais relevantes do esquema de Sarrus (aqueles que contêm i), ou se lembra da xyzzy sequência.
Desde a primeira diagonal no esquema de Sarrus é apenas o diagonal principal da acima -mentioned 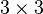 matriz, as três primeiras letras da palavra xyzzy pode muito facilmente ser lembrado.
matriz, as três primeiras letras da palavra xyzzy pode muito facilmente ser lembrado.
Aplicações
Geometria computacional
O produto cruzado pode ser utilizado para calcular a normal para um triângulo ou polígono, uma operação frequentemente realizada em gráficos de computador.
Em geometria computacional do plano , o produto cruzado é usado para determinar o sinal do ângulo agudo definido por três pontos 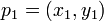 ,
, 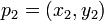 e
e 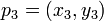 . Ele corresponde à direcção transversal do produto dos dois coplanares vectores definida pelos pares de pontos
. Ele corresponde à direcção transversal do produto dos dois coplanares vectores definida pelos pares de pontos 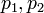 e
e 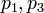 , Ou seja, pelo sinal da expressão
, Ou seja, pelo sinal da expressão 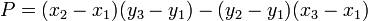 . No sistema "destro" coordenar, se o resultado for 0, os pontos estiverem alinhados; se for positivo, os três pontos de constitui um ângulo negativo de rotação em torno
. No sistema "destro" coordenar, se o resultado for 0, os pontos estiverem alinhados; se for positivo, os três pontos de constitui um ângulo negativo de rotação em torno 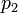 de
de 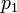 para
para 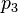 Caso contrário, um ângulo positivo. De outro ponto de vista, o sinal de
Caso contrário, um ângulo positivo. De outro ponto de vista, o sinal de 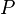 diz se
diz se 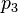 encontra-se à esquerda ou à direita da linha
encontra-se à esquerda ou à direita da linha  .
.
Outro
O produto transversal ocorre na fórmula para o operador vetorial curl. É também usado para descrever o Lorentz força experimentada por uma carga elétrica movendo-se em um campo magnético. As definições de torque e momento angular também envolvem o produto cruzado.
O truque de reescrever um produto transversal em termos de uma multiplicação de matrizes aparece freqüentemente em epipolar e multi-view geometria, em particular, ao derivar restrições correspondentes.
Cruz produto como um produto exterior
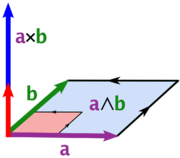
O produto vetorial pode ser visto em termos de produto exterior. Esta visão permite uma interpretação geométrica natural do produto cruzado. Em exterior cálculo do produto exterior (ou produto cunha) de dois vetores é um bivector. Um bivector é um elemento plano orientado, em muito da mesma maneira que um vector é um elemento de linha orientados. Dados dois vectores de a e b, pode-se ver o bivector um ∧ b como o paralelogramo orientado gerado por a e b. O produto cruzado é depois obtido pela Hodge dual do bivector um b ∧, identificando 2-vetores com vetores:
Isto pode ser pensado como o elemento multi-dimensional orientada "perpendicular" a bivector. Apenas em três dimensões é o resultado de um elemento orientado line - um vetor - que, por exemplo, em quatro dimensões do Hodge dual de um bivector é bidimensional - outro elemento plano orientado. Assim, em três dimensões só é o produto cruzado de a e b do vector dupla ao bivector um ∧ b: é perpendicular ao bivector, com orientação dependente de destreza manual do sistema de coordenadas, e tem a mesma ordem de grandeza em relação à unidade normal vector como um ∧ b tem em relação ao bivector unidade; precisamente as propriedades descritas acima.
Produto cruzado e lateralidade
Quando quantidades mensuráveis envolvem produtos cruzados, a lateralidade dos sistemas de coordenadas utilizados não pode ser arbitrária. No entanto, quando as leis da física são escritas como equações, deve ser possível fazer uma escolha arbitrária do sistema de coordenadas (incluindo destreza manual). Para evitar problemas, deve-se ter o cuidado de nunca escrever uma equação em que os dois lados não se comportam igualmente em todas as transformações que precisam ser considerados. Por exemplo, se um dos lados da equação é um produto cruzado de dois vectores, é preciso ter em conta que quando a destreza manual do sistema de coordenadas não está fixado a priori, o resultado não é um (verdadeiro), mas um vetor pseudovetor. Portanto, por razões de coerência, o outro lado também deve ser um pseudovetor.
De modo mais geral, o resultado de um produto de cruzamento pode ser um vector ou uma pseudovetor, dependendo do tipo dos seus operandos (vectores ou pseudovectors). Ou seja, vetores e pseudovectors estão inter-relacionadas das seguintes formas ao abrigo da aplicação do produto transversal:
- vector vector × = pseudovetor
- vector × pseudovetor = vector
- pseudovetor × pseudovetor = pseudovetor
Porque o produto transversal também pode ser um (verdadeiro) vector, não pode mudar de direcção com uma transformação da imagem de espelho. Isto acontece, de acordo com as relações acima, se um dos operandos é um (verdadeiro) vector e o outro é um pseudovetor (por exemplo, o produto cruzado de dois vectores). Por exemplo, uma vector produto triplo envolvendo três vectores (true) é um (verdadeiro) vector.
Uma abordagem livre de arbitrariedades é possível usando álgebra exterior.
Dimensões superiores
Existem vários caminhos para generalizar o produto cruzado para as dimensões superiores.
No contexto da álgebra multilinear, é possível definir um produto transversal generalizada em termos de de paridade de tal modo que o produto passe generalizada entre dois vectores de dimensão n é um inclinar-simétrica tensor de categoria N -2.
Usando octoniões
Um produto cruzado para vectores de 7-dimensional pode ser obtido da mesma maneira usando o octoniões em vez dos quaternions. A não existência de tais produtos cruzados de dois vectores em outras dimensões está relacionada com o resultado de que a única álgebras de divisão normados são os únicos com dimensão 1, 2, 4 e 8.
Produto Wedge
Em dimensão geral, não há nenhum análogo directa do produto cruzado binário. Existe no entanto o produto de cunha, que tem propriedades semelhantes, excepto que o produto cunha de dois vectores é agora um 2-vector, em vez de um vector comum. Como mencionado acima, o produto cruzado pode ser interpretado como o produto cunha em três dimensões utilizando depois Hodge dualidade para identificar 2-vetores com vectores.
Pode-se também construir um n análogo -ary do produto cruzado em R n +1 dada pelo
Esta fórmula é idêntico em estrutura com a fórmula determinante para o produto transversal normal em R 3, com excepção de que a linha de vectores de base, é a última linha no determinante em vez do primeiro. A razão para isto é assegurar que os vectores de pedidos (v 1, ..., n v, Λ (v 1, ..., v n)) têm uma positiva orientação em relação a (e 1, ..., n e 1). Se n é par, esta modificação deixa o valor inalterado, pelo que esta convenção concorda com a definição normal do produto binário. No caso em que n é ímpar, no entanto, deve ser mantida a distinção. Esta forma -ary n goza de muitas das mesmas propriedades do produto do vetor cruz: é alternada e linear em seus argumentos, é perpendicular a cada argumento e sua magnitude dá a hipervolume da região delimitada pelos argumentos. E, assim como o produto do vetor cruz, ele pode ser definido de forma independente como coordenar a Hodge dupla do produto cunha dos argumentos.
O produto da cunha e produto de ponto podem ser combinados para formar o Clifford produto.
História
Em 1773, Joseph Louis Lagrange introduziu a forma de componente, tanto do ponto e produtos cruzados, a fim de estudar o tetraedro em três dimensões. Em 1843, o físico e matemático Sir irlandês William Rowan Hamilton introduziu o quaternion produto, e com ele o "vector" termos e "escalar". Dado dois quaternions [0, u] e [0, v], onde uev são vetores em R3, seu produto quaternion pode ser resumido como [- u · v, u × v]. James Clerk Maxwell usou ferramentas quaternion de Hamilton para desenvolver suas famosas equações de eletromagnetismo e, por esta e outras razões quaternions por um tempo eram uma parte essencial da educação física.
No entanto, Oliver Heaviside na Inglaterra e Josiah Willard Gibbs em Connecticut sentiu que os métodos de quatérnios eram demasiado pesado, muitas vezes exigindo a parte escalar ou vetor de um resultado a ser extraído. Assim, cerca de 40 anos depois que o produto quaternion, o produto escalar e produto cruzado foram introduzidos - a oposição aquecida. Pivotal a (eventual) aceitação foi a eficiência da nova abordagem, permitindo Heaviside para reduzir as equações do eletromagnetismo do original 20 para os quatro comumente visto hoje de Maxwell.
Em grande parte independente desse desenvolvimento, e em grande parte desvalorizado no momento, Hermann Grassmann criou uma álgebra geométrica não vinculados a dimensão dois ou três, com o produto exterior que joga um papel central. William Kingdon Clifford combinou as álgebras de Hamilton e Grassmann para produzir Clifford álgebra, onde no caso de vectores tridimensional do bivector produzido a partir de dois vectores de dualizes a um vector, reproduzindo, assim, o produto cruzado.
A notação cruz, que começou com Gibbs, inspirou o nome "produto cruzado". Originalmente aparecendo em notícias publicadas em particular para seus alunos em 1881 como Elementos de Análise Vector, a notação de Gibbs - eo nome - mais tarde chegou a um público mais amplo através Análise vetorial (Gibbs / Wilson), um livro por um ex-aluno. Edwin Bidwell Wilson reorganizados material a partir palestras de Gibbs, em conjunto com material de publicações de Heaviside, Föpps, e Hamilton. Ele dividiu análise vetorial em três partes:
- "Em primeiro lugar, o que diz respeito a adição e as escalares e vetoriais produtos de vetores. Em segundo lugar, o que diz respeito ao cálculo diferencial e integral em suas relações com as funções escalares e vetoriais. Em terceiro lugar, aquele que contém a teoria da função do vetor linear."
Foram definidos dois tipos principais de multiplicações vetoriais, e eles foram chamados como segue:
- O escalar ou produto direto, ponto de dois vetores
- A inclinação, vetor, produto ou vetorial de dois vetores
Vários tipos de produtos triplos e produtos de mais de três vectores foram também examinados. A expansão do produto triplo acima mencionado também foi incluído.

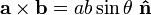
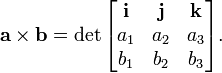
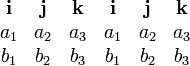
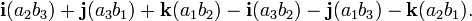
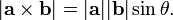
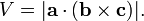
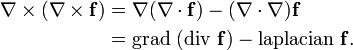
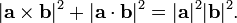
![\ Mathbf {a} \ times \ mathbf {b} = [\ mathbf {a}] _ {\ times} \ mathbf {b} = \ begin {bmatrix} \, 0 & \ - a_3 & \, \, a_2 \\ \, \, a_3 & 0 & \ - a_1 \\ - a_2 & \, \, a_1 & \, 0 \ end {bmatrix} \ begin {} bmatrix b_1 \\ \\ b_2 b_3 \ end {bmatrix}](../../images/212/21236.png)
![\ Mathbf {b} \ times \ mathbf {a} = [\ mathbf {a}] ^ T _ {\ times} \ mathbf {b} = \ begin {bmatrix} \, 0 & \, \, a_3 & \ - a_2 \ \ -a_3 & 0 & \, \, a_1 \\\, \, a_2 & \ - a_1 & \, 0 \ end {bmatrix} \ begin {} bmatrix b_1 \\ \\ b_2 b_3 \ end {bmatrix}](../../images/212/21237.png)
![[\ Mathbf {a}] _ {\ times} \ stackrel {\ rm def} {} = \ begin {bmatrix} \, \, 0 & \ - a_3 & \, \, \, a_2 \\\, \, \ , a_3 & 0 & \ - a_1 \\\ - a_2 & \, \, a_1 & \, \, 0 \ end {} bmatrix.](../../images/212/21238.png)
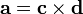
![[\ Mathbf {a}] _ {\ times} = (\ mathbf {c} \ mathbf {} d ^ T) ^ T - \ mathbf {c} \ mathbf {} d ^ T.](../../images/212/21240.png)
![\ Mathbf {b} ^ {T} \, [\ mathbf {a}] _ {} \ times \, \ mathbf {b} = 0.](../../images/212/21244.png)