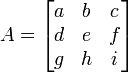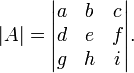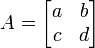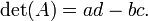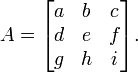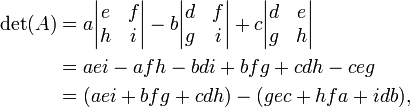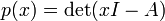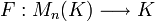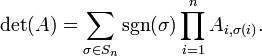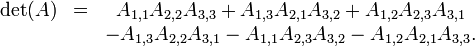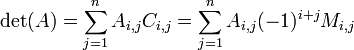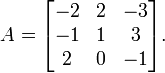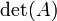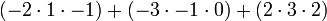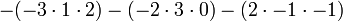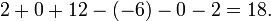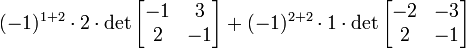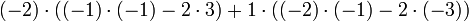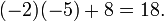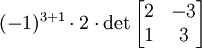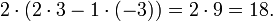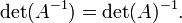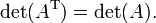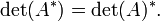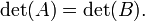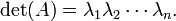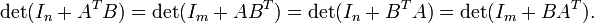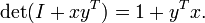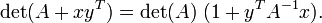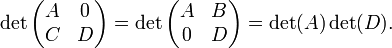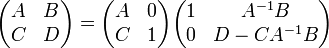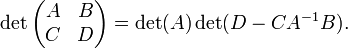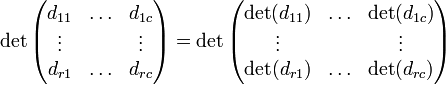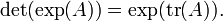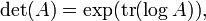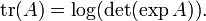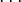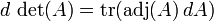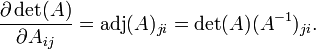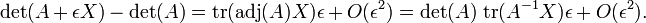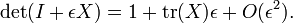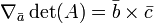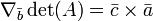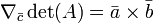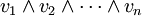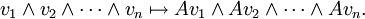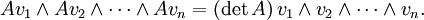Determinante
Você sabia ...
Arranjar uma seleção Wikipedia para as escolas no mundo em desenvolvimento sem internet foi uma iniciativa da SOS Children. patrocínio SOS Criança é legal!
Em álgebra , um determinante é uma função dependente de ne que associa um escalar, det (A), para cada n × n matriz quadrada A. O significado geométrico fundamental de um determinante é que o factor de escala para o volume quando A é considerada como um transformação linear. Determinantes são importantes tanto no cálculo , onde eles entram na regra de substituição para diversas variáveis, e em álgebra multilinear.
Para um número inteiro positivo n fixo, não é uma função única para o determinante N × n matrizes sobre qualquer anel conmutativo R. Em especial, existe esta função, quando R é a campo de reais ou números complexos .
Notação de barra vertical
O determinante de uma matriz A também é por vezes designado por | A |. Esta notação pode ser ambíguos uma vez que também é utilizada para certas normas da matriz e para o valor absoluto . No entanto, muitas vezes a norma matriz será denotado com barras verticais duplas (por exemplo, ‖ ‖ A) e pode transportar um subscrito também. Assim, a notação de barra vertical para determinante é freqüentemente utilizado (por exemplo, Regra de Cramer e menores). Por exemplo, para a matriz
o determinante 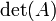 pode ser indicado pela
pode ser indicado pela 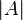 ou mais explicitamente como
ou mais explicitamente como
Isto é, as cintas em torno das matrizes quadrados são substituídas por barras verticais alongados.
Determinantes de matrizes 2-por-2

A matriz 2 x 2
tem determinante
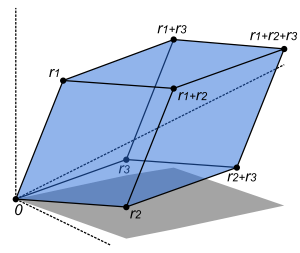
A interpretação quando a matriz tiver entradas de números reais é que este dá a área orientada do paralelogramo com os vértices (0,0), (a, b), (a + c, b + d), e (c, d). A área orientada é o mesmo que o habitual área , excepto que é negativo quando os vértices são listados na ordem dos ponteiros do relógio.
Supõe-se aqui que a transformação linear é aplicado à linha vectores como o produto do vetor-matriz 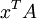 , Onde
, Onde 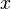 é um vector de coluna. O paralelogramo na figura é obtida multiplicando os vetores linha
é um vector de coluna. O paralelogramo na figura é obtida multiplicando os vetores linha  e
e 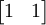 , Definindo os vértices do quadrado unitário. Com o produto matriz-vetor mais comum
, Definindo os vértices do quadrado unitário. Com o produto matriz-vetor mais comum 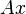 paralelogramo tem vértices em
paralelogramo tem vértices em 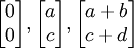 e
e  (Note que
(Note que 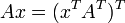 ).
).
Uma fórmula para matrizes maiores serão dadas a seguir.
Determinantes de matrizes 3-por-3
A matriz de 3 x 3:
Usando o expansão cofator na primeira linha da matriz temos:
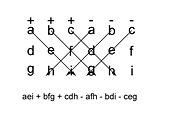
que pode ser lembrada como a soma dos produtos de três diagonal noroeste de linhas sudeste de elementos da matriz, menos a soma dos produtos dos três diagonal sudoeste de linhas nordeste de elementos quando as cópias da primeira duas colunas da matriz são escritos ao lado como a seguir:
Note que este mnemônico não transitar em dimensões superiores.
Aplicações
Determinantes são usados para caracterizar matrizes invertíveis (ou seja, exatamente essas matrizes com determinantes não-zero), e para descrever explicitamente a solução para um sistema de equações lineares com Regra de Cramer. Eles podem ser utilizados para encontrar os valores próprios da matriz  através de polinômio característico
através de polinômio característico
onde I é a matriz de identidade da mesma dimensão como A.
Um muitas vezes pensa do determinante como a atribuição de um número para cada seqüência de 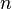 em vectores
em vectores 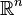 , Usando a matriz quadrada cujas colunas são os vetores dados. Com esse entendimento, o sinal do determinante de uma base pode ser usada para definir a noção de orientação em espaços euclidianos . O determinante de um conjunto de vetores é positivo se os vetores formam um destro sistema de coordenadas, e negativo se canhoto.
, Usando a matriz quadrada cujas colunas são os vetores dados. Com esse entendimento, o sinal do determinante de uma base pode ser usada para definir a noção de orientação em espaços euclidianos . O determinante de um conjunto de vetores é positivo se os vetores formam um destro sistema de coordenadas, e negativo se canhoto.
Determinantes são usadas para calcular os volumes de cálculo vectorial : o valor absoluto do determinante dos vectores reais é igual ao volume do paralelepípedo gerado por esses vetores. Em consequência, se o mapa linear 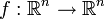 é representado pela matriz
é representado pela matriz  E
E 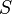 é qualquer mensurável subconjunto de
é qualquer mensurável subconjunto de 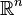 , Então o volume de
, Então o volume de 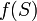 é dado pela
é dado pela 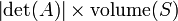 . De modo mais geral, se o mapa linear
. De modo mais geral, se o mapa linear 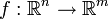 é representado pela
é representado pela 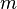 -by-
-by- 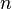 matriz
matriz  E
E 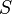 é mensurável qualquer subconjunto de
é mensurável qualquer subconjunto de 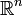 , Então o
, Então o 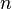 - o volume de dimensões
- o volume de dimensões 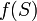 é dado pela
é dado pela 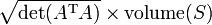 . Ao calcular o volume do tetraedro delimitada por quatro pontos, que podem ser usadas para identificar retas reversas.
. Ao calcular o volume do tetraedro delimitada por quatro pontos, que podem ser usadas para identificar retas reversas.
O volume de qualquer tetraedro , dado seus vértices a, b, c, e d, é (1/6) · | det (a - b, b - c, c - d) |, ou qualquer outra combinação de pares de vértices que formam um simplesmente conexa grafo.
Definição geral e computação
A definição do determinante vem do seguinte teorema.
Teorema. Deixe-M n (K) denotar o conjunto de todos 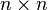 matrizes sobre o campo K. Não existe exatamente uma função
matrizes sobre o campo K. Não existe exatamente uma função
com as duas propriedades:
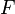 é alterno multilinear no que diz respeito a colunas;
é alterno multilinear no que diz respeito a colunas; 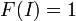 .
.
Pode-se então definir o determinante como a função original com as propriedades acima.
Ao provar o teorema acima, também se obtém o Leibniz fórmula:
Aqui a soma é calculado sobre todas as permutações 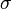 dos números {1,2, ..., n} e
dos números {1,2, ..., n} e 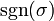 indica o assinatura da permutação
indica o assinatura da permutação 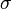 : 1 se
: 1 se 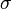 é um mesmo permutação e -1 se é ímpar.
é um mesmo permutação e -1 se é ímpar.
Esta fórmula inclui 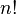 ( factorial ) summands, e é, por conseguinte, a usá-lo impraticável para calcular determinantes para grande
( factorial ) summands, e é, por conseguinte, a usá-lo impraticável para calcular determinantes para grande 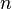 .
.
Para matrizes pequenas, obtém-se as seguintes fórmulas:
- se
 é uma matriz de um-por-um, então
é uma matriz de um-por-um, então 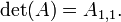
- se
 é uma matriz de duas-a-duas, então
é uma matriz de duas-a-duas, então 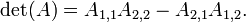
- para uma matriz de 3 por 3-
 , A fórmula é mais complicado:
, A fórmula é mais complicado:
que toma a forma do esquema Sarrus ' .
Em geral, os determinantes pode ser calculado utilizando a eliminação de Gauss utilizando as seguintes regras:
- Se
 é um matriz triangular, ou seja
é um matriz triangular, ou seja 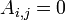 sempre que
sempre que 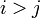 ou, alternativamente, quando
ou, alternativamente, quando 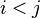 , Então
, Então 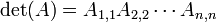 (O produto dos elementos da diagonal de
(O produto dos elementos da diagonal de  ).
). - Se
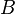 Resultados de
Resultados de  através da troca de duas linhas ou colunas, em seguida,
através da troca de duas linhas ou colunas, em seguida, 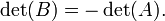
- Se
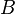 Resultados de
Resultados de  multiplicando uma linha ou coluna com o número
multiplicando uma linha ou coluna com o número  , Então
, Então 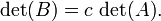
- Se
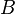 Resultados de
Resultados de  por adição de um múltiplo de uma fila para outra linha, ou um múltiplo de uma coluna para outra coluna, seguida
por adição de um múltiplo de uma fila para outra linha, ou um múltiplo de uma coluna para outra coluna, seguida 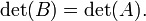
Explicitamente, iniciando-se com alguma matriz, use os últimos três regras para convertê-lo em uma matriz triangular, em seguida, usar a primeira regra para calcular o seu determinante.
É também possível expandir um determinante ao longo de uma linha ou coluna usando Fórmula de Laplace, que é eficiente relativamente pequenos matrizes. Para fazer isso ao longo linha 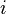 , Por exemplo, nós escrevemos
, Por exemplo, nós escrevemos
onde o 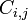 representar a matriz cofactores, ou seja
representar a matriz cofactores, ou seja 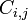 é
é 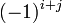 vezes o menor
vezes o menor 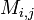 , Que é o determinante da matriz que resulta
, Que é o determinante da matriz que resulta  removendo o
removendo o 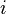 linha -th eo
linha -th eo 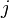 -th coluna.
-th coluna.
Exemplo
Suponha que queremos calcular o determinante de
Podemos ir em frente e utilizar a fórmula Leibniz diretamente:
Alternativamente, podemos usar Fórmula de Laplace para expandir o determinante ao longo de uma linha ou coluna. É melhor escolher uma linha ou coluna com muitos zeros, então vamos expandir ao longo da segunda coluna:
Uma terceira forma (e o método de escolha para matrizes maiores) envolveria o algoritmo de Gauss. Ao fazer cálculos à mão, pode-se muitas vezes encurtar as coisas de forma dramática por inteligentemente acrescentando múltiplos de colunas ou linhas para outras colunas ou linhas; esta não muda o valor do determinante, mas podem criar entradas de zero o que simplifica os cálculos subsequentes. Neste exemplo, a adição da segunda coluna para a primeira é especialmente útil:
e esse determinante pode ser rapidamente expandido ao longo da primeira coluna:
Propriedades
O determinante é um mapa multiplicativo no sentido de que
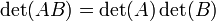 para todo n -by- n matrizes
para todo n -by- n matrizes  e
e 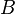 .
.
Este é generalizada pela Cauchy-Binet fórmula para produtos de matrizes não-quadrados.
É fácil ver que 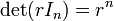 e assim
e assim
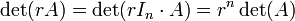 para todos
para todos 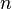 -by-
-by- 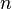 matrizes
matrizes  e tudo escalares
e tudo escalares  .
.
Uma matriz sobre um anel comutativo R é inversível se e somente se seu determinante é um unidade em R. Em particular, se A é uma matriz ao longo de um campo, tais como os verdadeiros ou números complexos , então A é invertível se, e apenas se det (A) não é igual a zero. Neste caso, temos
Dito de outro modo: os vetores v 1, ..., v n em R n formar um base, se e somente se det (v 1, ..., v n) é diferente de zero.
Uma matriz e sua transpor têm o mesmo determinante:
Os determinantes de uma matriz complexa e de sua transposta conjugada são conjugado:
(Note-se a transposta conjugada é idêntico para a transposta para uma matriz real)
O determinante de uma matriz  exibe as seguintes propriedades sob transformações de matrizes elementares de
exibe as seguintes propriedades sob transformações de matrizes elementares de  :
:
- Trocar linhas ou colunas multiplica o determinante por -1.
- A multiplicação de uma linha ou coluna
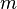 multiplica o determinante por
multiplica o determinante por 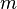 .
. - A adição de um múltiplo de uma linha ou coluna para outro deixa inalterado o determinante.
Isso decorre da propriedade multiplicativa e os determinantes da matrizes de transformação matriz elementares.
Se  e
e 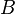 são semelhante, ou seja, se existe uma matriz invertível
são semelhante, ou seja, se existe uma matriz invertível 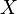 tal que
tal que  =
= 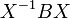 , Seguida pela propriedade multiplicativa,
, Seguida pela propriedade multiplicativa,
Isto significa que o determinante é um similaridade invariante. Devido a isso, o determinante de alguma transformação linear T: V → V para alguns finito dimensional espaço vectorial V é independente da base de V. A relação é de um só sentido, no entanto: existem matrizes que têm o mesmo determinante, mas não são semelhantes.
Se  é um quadrado
é um quadrado 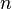 -by-
-by- 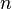 matriz com reais ou complexos entradas e se λ 1, ..., λ n são os (complexos) valores próprios de
matriz com reais ou complexos entradas e se λ 1, ..., λ n são os (complexos) valores próprios de  listados de acordo com suas multiplicidades algébricas, em seguida,
listados de acordo com suas multiplicidades algébricas, em seguida,
Isso decorre do fato de que  é sempre semelhante ao seu Jordan forma normal, uma matriz triangular superior com os valores próprios na diagonal principal.
é sempre semelhante ao seu Jordan forma normal, uma matriz triangular superior com os valores próprios na diagonal principal.
Identidades úteis
Para m -by- n matriz A e m -by- n matriz B, que detém
A conseqüência dessas igualdades para o caso de (coluna) vetores x e y
E uma versão generalizada desta identidade
As provas podem ser encontrados em .
Matrizes do Bloco
Suponha-se, 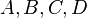 são
são 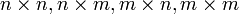 matrizes respectivamente. Em seguida
matrizes respectivamente. Em seguida
Isto pode ser (muito) facilmente visto a partir de por exemplo, a Fórmula Leibniz. Empregando-se o seguinte identidade
leva a
Identidade semelhante com 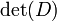 fora consignado pode ser derivado de forma análoga. Estas identidades foram tomadas a partir de .
fora consignado pode ser derivado de forma análoga. Estas identidades foram tomadas a partir de .
Se 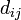 são matrizes diagonais, então
são matrizes diagonais, então
Este é um caso especial do teorema publicado em .
Relação com traço
A partir desta ligação entre o determinante e os valores próprios, pode-se derivar uma ligação entre o função de rastreamento, a função exponencial, e o determinante:
Realizando a substituição 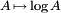 nos rendimentos equação acima
nos rendimentos equação acima
que está intimamente relacionado com o Determinante Fredholm. Da mesma forma,
Para n -by- matrizes n existem as relações:
- Caso n = 1:
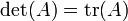
- Caso n = 2:
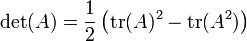
- Caso n = 3:
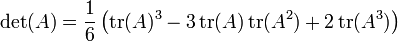
- Caso n = 4:
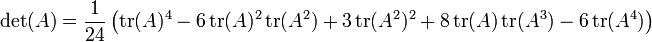
que estão intimamente relacionados com Identidades de Newton.
Derivado
O determinante de matrizes quadradas reais é uma função polinomial de 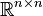 para
para 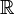 , E como tal está em toda parte diferenciável . Seu derivado pode ser expressa usando A fórmula de Jacobi:
, E como tal está em toda parte diferenciável . Seu derivado pode ser expressa usando A fórmula de Jacobi:
onde adj (A) indica o adjugate de A. Em particular, se A é invertível, temos
Na forma de componente, estes são
Quando  é um pequeno número estes são equivalentes às
é um pequeno número estes são equivalentes às
O caso especial onde  é igual à matriz identidade
é igual à matriz identidade 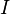 rendimentos
rendimentos
Uma propriedade útil no caso de matrizes de 3 X 3 é o seguinte:
A pode ser escrito como 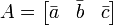 onde
onde 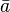 ,
, 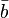 ,
, 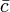 Os vectores são, em seguida, o gradiente ao longo de um dos três vectores pode ser escrita como o produto cruzado dos outros dois:
Os vectores são, em seguida, o gradiente ao longo de um dos três vectores pode ser escrita como o produto cruzado dos outros dois:
Formulação abstrata
Um N × n matriz quadrada A pode ser considerado como a representação de uma coordenada transformação linear de um n-dimensional espaço vetorial V. Dado qualquer transformação linear
podemos definir o determinante de A como o determinante de qualquer representação de matriz A. Isto é um noção bem definido (isto é, independente da escolha de um base) desde o determinante é invariante sob transformações de similaridade.
Como se poderia esperar, é possível definir o determinante de uma transformação linear de uma forma coordenada livre. Se V é um espaço n -dimensional vector, em seguida, pode-se construir seu topo exterior poder Λ n V. Este é um espaço vectorial unidimensional cujos elementos são escritos
onde cada v i é um vector em V e o ∧ produto cunha é anti-simétrica (ie, u ∧ u = 0). Qualquer transformação linear A: V → V induz uma transformação linear de Λ n V da seguinte forma:
Desde Λ n V é unidimensional esta operação é apenas multiplicação por alguns escalar que depende de uma. Isso é chamado de escalar o determinante de A. Ou seja, nós definimos det (A) pela equação
Pode-se verificar que essa definição está de acordo com a definição coordenada dependente dado acima.
Implementação algorítmica
- O método ingênuo da implementação de um algoritmo para calcular o determinante é usar a fórmula de Laplace para a expansão de cofatores. Esta abordagem é extremamente ineficiente, em geral, no entanto, como é de ordem n! (N factorial ) para uma matriz n × n M.
- Uma melhoria de ordem n 3 pode ser conseguido através da utilização LU decomposição de escrever M = LU para triangular matrizes L e U. Agora, det M = det LU = det L det U, e uma vez que L e U são triangular o determinante de cada um é simplesmente o produto de seus elementos diagonais. Em alternativa, é possível realizar o Cholesky decomposição se possível, ou a QR decomposição e encontrar o determinante de uma forma semelhante.
- Desde a definição do determinante não precisa divisões, surge uma questão: será que existem algoritmos rápidos que não necessitam de divisões? Isto é especialmente interessante para matrizes mais anéis. Na verdade algoritmos com tempo de execução proporcional ao n 4 existir. Um algoritmo de Mahajan e Vinay, e baseia-se na Berkowitz caminhadas encomendados fechados (curto clow). Ele calcula mais produtos que requer a definição determinante, mas alguns desses produtos e cancelar a soma destes produtos pode ser calculado de forma mais eficiente. O algoritmo final se parece muito com um produto iterado de matrizes triangulares.
- O que não é frequentemente discutido é o chamado "complexidade bits" do problema, isto é, quantos bits de precisão é necessário armazenar para valores intermédios. Por exemplo, usando a eliminação de Gauss , você pode reduzir a matriz de forma triangular, em seguida, multiplicar a diagonal principal para obter o determinante (este é essencialmente um caso especial da decomposição LU como acima), mas um cálculo rápido mostra que o bit tamanho dos valores intermediários poderia potencialmente se tornar exponencial. Pode-se falar sobre quando é apropriado para arredondar os valores intermédios, mas uma maneira elegante de calcular o determinante usa o Bareiss Algorithm, um método exato-divisão com base em Identidade de Sylvester para dar um tempo de execução de ordem n 3 e complexidade pouco mais ou menos do tamanho das entradas originais nos tempos matriz n bits.
História
Historicamente, determinantes foram consideradas antes de matrizes. Originalmente, um determinante foi definido como uma propriedade de um sistema de equações lineares . O determinante "determina" se o sistema tem uma solução única (o que ocorre precisamente quando o determinante é diferente de zero). Neste sentido, foram determinantes usado pela primeira vez no livro de matemática BC chinês do século 3 Os Nove Capítulos da Arte Matemática. Na Europa, dois dois-por-determinantes foram consideradas pela Cardano no final do século 16 e as maiores por Leibniz e, no Japão, por Seki cerca de 100 anos mais tarde. Cramer (1750) adicionado à teoria, tratando o assunto em relação a conjuntos de equações. A lei recorrente foi anunciado pela primeira vez por Bézout (1764).
Era Vandermonde (1771) que foi o primeiro determinantes reconhecidos como funções independentes. Laplace (1772) deu o método geral de expansão de um determinante em termos da sua complementar menores: Vandermonde já tinha dado um caso especial. Imediatamente após, Lagrange (1773) tratados determinantes da segunda e terceira ordem. Lagrange foi o primeiro a aplicar determinantes para perguntas teoria eliminação; ele provou muitos casos especiais de identidades gerais.
Gauss (1801) fez a seguinte antecedência. Como Lagrange, ele fez muito uso de determinantes na teoria dos números . Ele introduziu a palavra determinantes (Laplace tinha usado resultante), embora não no presente significação, mas sim como aplicado ao discriminante de um quântico. Gauss também chegou à noção de (inversas) determinantes recíprocas, e chegou muito perto do teorema de multiplicação.
O próximo colaborador de importância é Binet (1811, 1812), que declarou formalmente o teorema relativo ao produto de duas matrizes de m colunas e n linhas, o que para o caso especial de m = n reduz com o teorema de multiplicação. No mesmo dia ( 30 de novembro de 1812 ), que Binet apresentou seu papel para a Academia, Cauchy também apresentou uma sobre o assunto. (Ver Fórmula de Cauchy-Binet.) Neste ele usou a palavra determinante em seu sentido atual, resumidas e simplificado que era então conhecido sobre o assunto, melhorou a notação, e deu o teorema de multiplicação com uma prova mais satisfatória do que Binet de. Com ele começa a teoria em sua generalidade.
A próxima figura importante foi Jacobi (de 1827). Muito cedo ele usou o determinante funcional que mais tarde chamado de Sylvester Jacobian, e em suas memórias em Crelle para 1841 especialmente trata este assunto, bem como a classe de funções que Sylvester chamou alternants alternada. Sobre o tempo dos últimos memórias de Jacobi, Sylvester (1839) e Cayley começou seu trabalho.
O estudo de formas especiais de determinantes tem sido o resultado natural da conclusão da teoria geral. Axissimétricos determinantes têm sido estudados por Lebesgue, Hesse, e Sylvester; determinantes persymmetric por Sylvester e Hankel; circulants por Catalão, Spottiswoode, Glaisher, e Scott; determinantes de inclinação e Pfaffianas, em conexão com a teoria da transformação ortogonal, por Cayley; continuants por Sylvester; Wronskians (assim chamado por Muir) pela Christoffel e Frobenius; determinantes compostos por Sylvester, Reiss, e Picquet; Jacobianos e Hessians por Sylvester; e simétricas determinantes gauche por Trudi. Dos livros-texto sobre o assunto Spottiswoode foi a primeira. Na América, Hanus (1886), Weld (1893), e Muir / Metzler (1933) publicaram tratados.