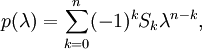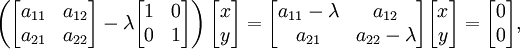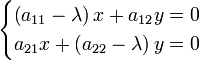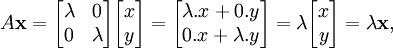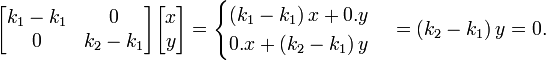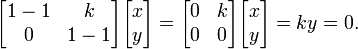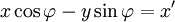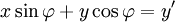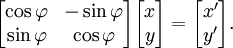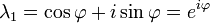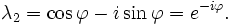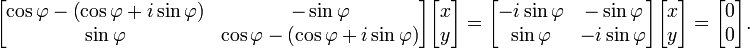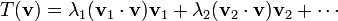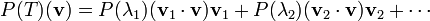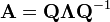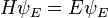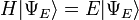Valores e vectores próprios
Informações de fundo
Crianças SOS feita esta seleção Wikipedia ao lado de outras escolas recursos . Veja http://www.soschildren.org/sponsor-a-child para saber mais sobre apadrinhamento de crianças.

Em matemática , um vector pode ser pensado como uma seta. Tem um comprimento, chamado de sua magnitude, e ele aponta em uma direção particular. A transformação linear pode ser considerada para operar em um vetor para mudá-la, geralmente mudando tanto a sua magnitude e sua direção. Um vector próprio de uma determinada transformação linear é um vector que é multiplicado por uma constante chamada Eigenvalue durante essa transformação. A direcção do vector próprio ou é inalterada por essa transformação (para valores próprios positivos) ou reversa (de valores próprios negativos).
Por exemplo, um valor próprio de 2 significa que o vector próprio é dobrada em comprimento e pontos na mesma direcção. Um valor próprio de um significa que o vector próprio não é alterada, enquanto que um valor próprio de -1 significa que o autovetor é revertida em direção. Um auto-espaço de uma dada extensão é a transformação dos vectores próprios de que a transformação com o mesmo valor próprio, em conjunto com o vector de zero (que não tem qualquer sentido). Um auto-espaço é um exemplo de um subespaço de um espaço vetorial .
Em álgebra linear , toda transformação linear entre espaços vetoriais de dimensão finita pode ser dada por uma matriz , que é uma matriz retangular de números organizados em linhas e colunas. Métodos padrão para encontrar valores próprios, vectores próprios, e autoespaços de uma dada matriz são discutidos abaixo.
Estes conceitos desempenhar um papel importante em vários ramos de ambos pura e matemática aplicada - que aparece com destaque na álgebra linear , análise funcional, e em menor grau em matemática não-linear.
Muitos tipos de objetos matemáticos podem ser tratados como vetores: funções , modos harmônicos, estados quânticos, e frequências, por exemplo. Nestes casos, o conceito de sentido perde o seu significado comum, e é dada uma definição abstracta. Mesmo assim, se esta direcção resumo é inalterada por uma transformação linear dado, o prefixo "eigen" é usado, como em eigenfunction, modo próprio, auto-estado, e frequ�cia pr�ria.
História
Valores próprios são muitas vezes introduzidos no contexto da álgebra linear ou teoria da matriz . Historicamente, no entanto, levantaram-se no estudo de quadrática formas e equações diferenciais .
Euler estudaram também o movimento de rotação de um corpo rígido e descobriu a importância do eixos principais. Como Lagrange realizado, os eixos principais são os autovetores da matriz de inércia. No início do século 19, Cauchy viu como o seu trabalho pode ser usada para classificar a quádricas, e generalizado para dimensões arbitrárias. Cauchy também cunhou o termo caractéristique Racine (root característica) para o que agora é chamado de valor próprio; seu mandato sobrevive em equação característica.
Fourier utilizado o trabalho de Laplace e Lagrange para resolver o equação do calor por separação de variáveis em seu famoso livro 1822 Théorie analytique de la chaleur. Sturm desenvolvido idéias de Fourier mais e trouxe-os para a atenção de Cauchy, que lhes combinado com suas próprias idéias e chegou ao fato de que matrizes simétricas têm valores próprios reais. Este foi prorrogado por Hermite em 1855 para o que hoje é chamado Hermitianas matrizes. Na mesma época, Brioschi provou que os valores próprios de matrizes ortogonais mentir sobre o círculo unitário, e Clebsch encontrado o resultado correspondente para inclinar-simétricas matrizes. Finalmente, Weierstrass clarificado um aspecto importante na teoria de estabilidade iniciado por Laplace por perceber que matrizes com defeito pode causar instabilidade.
Entretanto, Liouville estudada de valores próprios problemas semelhantes aos de Sturm; a disciplina que cresceu a partir do seu trabalho agora é chamado Teoria de Sturm-Liouville. Schwarz estudou o primeiro autovalor de A equação de Laplace em domínios gerais no final do século 19, enquanto Poincaré estudado A equação de Poisson alguns anos mais tarde.
No início do século 20, Hilbert estudou os valores próprios de operadores integrais por visitar os operadores como matrizes infinitas. Ele foi o primeiro a usar o alemão palavra eigen para denotar valores e vectores próprios em 1904, embora ele pode ter sido na sequência de uma utilização relacionada por Helmholtz. "Eigen" pode ser traduzido como "tenho", "peculiar a", "característica" ou "indivíduo" -emphasizing quão importante são valores próprios para a definição da natureza única de uma transformação específica. Por algum tempo, o termo padrão em Inglês foi "valor próprio", mas o mais distintivo termo "valor próprio" é padrão hoje.
O primeiro algoritmo numérico para calcular valores e vetores próprios apareceu em 1929, quando Von Mises publicou o método de alimentação. Um dos métodos mais populares de hoje, o Algoritmo QR, foi proposta de forma independente por Francis e Kublanovskaya em 1961.
Definições: a equação de valor próprio
Transformações lineares de um espaço vectorial, como rotação, reflexão, alongamento, compressão, cisalhamento ou qualquer combinação destes, pode ser visualizada pelo efeito que produzem em vectores . Em outras palavras, eles são funções do vector. Mais formalmente, num espaço vectorial G uma função vectorial, se A é definido para cada vector x de L corresponde um único vector y = A (x) de L. Por uma questão de brevidade, os parêntesis ao redor do vector em que a transformação é que actuam muitas vezes são omitidos. Um vector de função A é linear, se ele tem as duas propriedades seguintes:
- aditividade
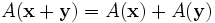
- homogeneidade
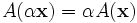
em que x e y são quaisquer dois vectores do espaço vectorial L e α é qualquer número real . Tal função é variadamente chamado uma transformação linear, operador linear, ou linear endomorphism no espaço G.
Dado uma transformação linear A, um non-zero vetor x é definido como sendo um vector próprio da transformação se satisfaz a equação autovalor A x = λ x para alguns λ escalar. Nesta situação, o λ escalar é chamado um valor próprio correspondente de A para o vector próprio x. |
A equação fundamental nesta definição é a equação valor próprio, A x = λ x. A maioria dos vetores x não irá satisfazer tal equação. Um típico vetor x muda de direcção, quando actuado por uma, de modo que A x não é um múltiplo de x. Isto significa que apenas certos vectores especiais X são vectores próprios, e apenas certos λ números especiais são valores próprios. Claro que, se A for um múltiplo do matriz de identidade, então nenhum vetor muda de direção e todos os vetores não nulos são vectores próprios. Mas, no caso de costume, autovetores são poucos e distantes entre si. Eles são os modos "normal" do sistema, e que actuam de forma independente.
A exigência de que o vector próprio ser diferente de zero é imposta porque a equação A 0 = λ 0 é válida para todos os A e cada λ. Como a equação é sempre trivialmente verdadeira, não é um caso interessante. Em contraste, um valor próprio pode ser zero de uma forma não trivial. Um valor próprio pode ser, e normalmente é, também um número complexo . Na definição dada acima, autovetores e autovalores não ocorrem de forma independente. Em vez disso, cada vector próprio está associado com um valor próprio específica. Por esta razão, um vector próprio x e um valor próprio correspondente λ são muitas vezes referida como uma eigenpair. Um valor próprio pode ser associado a vários ou mesmo com número infinito de vectores próprios. Mas por outro lado, se um autovetor é dado, o valor próprio associado para este eigenvector é único. Com efeito, a partir da igualdade A x = λ x = λ 'x e de x ≠ 0, conclui-se que λ = λ'.

Geometricamente (Fig. 2), a equação de valores próprios significa que sob a transformação vectores próprios uma experiência apenas alterações na grandeza e sinal - a direcção de A x é a mesma que a de x. Este tipo de transformação é definido como linear homothety (dilatação, transformação de similaridade). O valor próprio λ é simplesmente a quantidade de "estiramento" ou "encolher" para que um vector se submete quando transformado por um. Se λ = 1, o vector permanece inalterada (não afectada pela transformação). Uma transformação eu sob a qual um vetor x permanece inalterada, I x = x, é definida como transformação de identidade. Se λ = -1, o vector vira na direcção oposta (gira a 180 °); esta é definida como reflexão.
Se x é um autovetor da transformação linear A, com valor próprio λ, então qualquer vector y = x α também é um autovetor de A com o mesmo valor próprio. A partir da homogeneidade da transformação Um Daqui resulta que um Y = α (A x) = α (λ x) = λ (α x) y = λ. Da mesma forma, usando a propriedade de aditividade da transformação linear, pode-se mostrar que qualquer combinação linear de vectores próprios com valor próprio λ tem o mesmo valor próprio λ. Portanto, qualquer vector diferente de zero na linha através x e o vector de zero é um vector próprio com o mesmo valor próprio como x. Juntamente com o vetor zero, esses autovetores formam um subespaço do espaço vetorial chamado de auto-espaço. Os autovetores correspondentes a diferentes valores próprios são linearmente significado independente, em particular, que, em um espaço n-dimensional a transformação linear Um não pode ter mais de n autovetores com diferentes valores próprios. Os vectores da autoespaço gerar um subespaço linear de A que é invariante (inalterado) sob essa transformação.
Se um base é definido no espaço vectorial G n, todos os vectores pode ser expresso em termos de componentes . Vectores polares podem ser representados como matrizes de uma coluna com n linhas, onde n é o dimensionalidade. Transformações lineares podem ser representados com matrizes quadradas; para cada transformação linear de A L n corresponde uma matriz quadrada de posto n. Por outro lado, para cada matriz quadrada de posto n corresponde uma transformação linear de L n a uma dada base. Por causa da aditividade e homogeneidade da trasformation linear e o valor próprio equação (que é também uma transformação linear - homotetia), as funções vector pode ser expresso em forma de matriz. Assim, em uma a duas dimensões vector espaço L equipado com dois base padrão, a equação eigenvector para uma transformação linear A pode ser escrita na seguinte representação matricial:
em que a justaposição de matrizes significa a multiplicação de matrizes . Isto é equivalente a um conjunto de equações lineares n, onde n é o número de vectores de base no base definida. Nestas equações tanto o λ valores próprios e os componentes de x são desconhecidos variáveis.
Os vectores próprios de A, tal como definidos acima também são chamados vectores próprios certos porque são vectores de coluna que se encontra no lado direito da matriz A na equação valor próprio. Se existir uma matriz transposta Um T que satifies a equação valor próprio, isto é, se a t x = λ x, então λ x = T (λ x) T = (A x T) T = x T A, T ou X A = λ x T. A última equação é semelhante à equação de valores próprios mas, em vez do vector x de coluna que contém o seu vector transposto, a linha vetor x T, que fica do lado esquerdo da matriz A. Os vectores próprios que satisfazem a equação x autovalor T A = λ x T são chamados autovetores esquerdos. Eles são vetores linha. Em muitas aplicações comuns, apenas certos vectores próprios devem ser considerados. Por isso, o termo não qualificado "vector próprio" pode ser entendida para se referir a um vector próprio direito. Equações de valores próprios, escritos em termos de autovetores direita ou à esquerda (A x = λ x e T x A = λ x T) têm o mesmo valor próprio λ.
Um autovetor é definida para ser um diretor ou autovetor dominante se corresponde ao valor próprio de maior magnitude (para números reais, maior valor absoluto). A aplicação repetida de uma transformação linear para um arbitrárias vector resulta em um vetor proporcional (colineares) com o vector próprio diretor.
A aplicabilidade da equação de valor próprio a teoria da matriz geral estende-se a utilização de vectores próprios e valores próprios para todas as matrizes, e assim grandemente alarga o âmbito da utilização destas construções matemáticas não só para transformações em espaços vetoriais lineares, mas a todos os campos da ciência que utilizam matrizes: linear equações sistemas, otimização, vector e cálculo tensor, todos os campos da física que usam quantidades de matriz, a física quântica, a relatividade especial e eletrodinâmica, assim como muitas aplicações de engenharia.
Equação característica
A determinação dos valores e vetores próprios é importante em praticamente todas as áreas da física e muitos problemas de engenharia, tais como cálculos de estresse, análise de estabilidade, oscilações de sistemas de vibração, etc. Ele é equivalente a diagonalização matriz, e é o primeiro passo de ortogonalização, encontrando de invariantes, otimização (maximização ou minimização), análise de sistemas lineares, e muitas outras aplicações comuns.
O método usual de encontrar todos os vectores próprios e valores próprios de um sistema é o primeiro a se livrar dos componentes desconhecidos dos vectores próprios, em seguida, encontrar os valores próprios, conecte aqueles de volta um por um na equação de valor próprio na forma matricial e resolver isso como um sistema de equações lineares para encontrar os componentes dos vectores próprios. A partir da transformação de identidade I x = x, onde I é a matriz de identidade, x na equação valor próprio pode ser substituído por I x para dar:
A matriz de identidade é necessária para manter as matrizes, vetores e escalares em linha reta; a equação (A - λ) x = 0 é mais curto, mas misturados uma vez que não faz distinção entre a matriz, escalar e vetor. A expressão no lado direito é transferido para o lado esquerdo com um sinal negativo, deixando 0 no lado direito:
O autovetor x é puxada para trás parênteses:
Isto pode ser visto como um sistema de equações lineares , em que a matriz é o coeficiente de expressão dentro dos parêntesis, a matriz dos desconhecidos é x, e a matriz lado direito é zero. Conforme Regra de Cramer, este sistema de equações tem soluções não triviais (nem todos os zeros, ou não qualquer número) se e somente se seu determinante desaparece, assim que as soluções da equação são dadas por:
Esta equação é definido como o equação característica (com menos frequência, equação temporal) de A, e o lado esquerdo é definido como a polinômio característico. O x eigenvector ou seus componentes não estão presentes na equação característica, por isso, nesta fase, eles são dispensados, e as únicas incógnitas que ainda precisam ser calculados são os valores próprios (os componentes da matriz A são dadas, i. E, sabe de antemão ). Para um espaço vetorial L 2, a transformação A é uma matriz quadrada 2 × 2, ea equação característica pode ser escrito da seguinte forma:
Expansão do determinante nos resultados do lado esquerdo em um polinômio característico que é um monic (seu coeficiente de liderança é 1) polinômio do segundo grau, e a equação característica é a equação quadrática
que tem as seguintes soluções ( raízes):
Para matrizes de reais, os coeficientes do polinômio característico são todos real. O número e tipo de raízes depende do valor do discriminante, D. Para os casos D = 0, D> 0, ou D <0, respectivamente, as raízes são um real, dois real, ou dois complexos. Se as raízes são complexos, eles são também Os conjugados complexos de cada outro. Quando o número de raízes é menos do que o grau do polinómio característica (o último é também a posição da matriz, e o número de dimensões de espaço vectorial a) a equação tem uma raiz múltipla. No caso de uma equação quadrática com uma raiz, esta raiz é uma raiz dupla, ou com uma raiz 2. Uma multiplicidade de raiz com uma multiplicidade de 1 é uma raiz simples. A equação quadrática com duas raízes reais ou complexos tem raízes única simples. Em geral, o algébrico multiplicidade de um valor próprio é definida como a multiplicidade de raiz correspondente do polinômio característico. O espectro de uma transformação em uma dimensão finita de espaço vectorial é definida como a conjunto de todos os seus valores próprios. No caso de dimensão infinita, o conceito de espectro é mais subtil e depende da topologia do espaço vectorial.
A fórmula geral para o polinómio característico de uma matriz n é quadr
onde S 0 = 1, S = 1 tr (A), o traço da matriz de transformação A, e S k com k> 1 são as somas de o principal menores de ordem k. O facto de valores próprios são raízes de uma N -order equação mostra que uma transformação linear de um espaço n-dimensional linear tem no máximo n valores próprios diferentes. De acordo com teorema fundamental da álgebra, num espaço linear complexo, o polinomial característica tem, pelo menos, um zero. Por conseguinte, cada transformação linear de um espaço linear complexo tem pelo menos um valor próprio. Para espaços lineares reais, se a dimensão for um número ímpar, a transformação linear tem pelo menos um valor próprio; Se a dimensão for um número par, o número de valores próprios depende do determinante da matriz de transformação: se o determinante é negativo, existe, pelo menos, uma positiva e outra negativa valor próprio, se o determinante é nada positiva pode ser dito acerca da existência valores próprios. A complexidade do problema para encontrar raízes / valores próprios da característica aumenta polinomiais rapidamente com o aumento do grau do polinómio (a dimensão do espaço vectorial), n. Assim, para n = 3, valores próprios são raízes da equação cúbica, para n = 4 - raízes da equação quártica. Para n> 4 não existem soluções exatas e um tem que recorrer a algoritmos de busca de raiz, tais como o método de Newton ( O método de Horner) para encontrar aproximações numéricas de valores próprios. Para grande simétrica matrizes esparsas, Algoritmo de Lanczos é usado para calcular valores e vetores próprios.
A fim de encontrar os vectores próprios, os valores próprios deste modo encontrados como raízes das equações características estão ligados para trás, um de cada vez, na equação valor próprio escrita em forma de matriz (ilustrada para o caso mais simples de um vector bidimensional espaço L2 ):
onde λ é um dos valores próprios encontrados como uma raiz da equação característica. Esta equação da matriz é equivalente a um sistema de duas equações lineares:
As equações são resolvidas para x e y pelos métodos habituais algébricas ou matriz. Muitas vezes, é possível dividir ambos os lados das equações para um ou mais dos coeficientes que torna alguns dos coeficientes em frente dos desconhecidos iguais a 1. Isto é chamado normalização dos vectores, e corresponde a escolher um dos vectores eigen (o vector próprio normalizado) como um representante de todos os vectores em autoespaço correspondente ao respectivo valor próprio. O x e y, portanto, são encontrados os componentes do vector próprio no sistema de coordenadas utilizados (na maioria das vezes cartesiano, ou polar).
Usando o Cayley-Hamilton teorema que afirma que cada matriz quadrada satisfaz sua própria equação característica, pode ser demonstrado que (mais geralmente, no espaço complexo) existe pelo menos um vector diferente de zero que satisfaz a equação de valores próprios para essa matriz. Como foi dito na seção Definições, para cada valor próprio corresponder um número infinito de colineares autovetores linearmente (dependentes) que formam a eigenspace para este valor próprio. Por outro lado, a dimensão da autoespaço é igual ao número dos vectores eigen linearmente independentes que ele contém. A multiplicidade geométrica de um valor próprio é definida como a dimensão do autoespaço associado. Um valor próprio múltiplo pode dar origem a um único vector próprio de modo a que a sua multiplicidade algébrica pode ser diferente do que a multiplicidade geométrica. No entanto, como já foi dito, diferentes valores próprios estão emparelhados com autovetores linearmente independentes. A partir do acima mencionado, segue-se que a multiplicidade geométrica não pode ser maior do que a multiplicidade algébrico.
Por exemplo, um vector próprio de uma rotação em três dimensões é um vector localizado dentro do eixo em torno do qual a rotação é realizada. O valor próprio correspondente é 1 e o correspondente autoespaço contém todos os vectores ao longo do eixo. Como este é um espaço unidimensional, a sua multiplicidade é um geométrico. Este é o único valor próprio do espectro (esta de rotação), que é um número real .
Exemplos
Os exemplos que se seguem são para o caso mais simples de bi-dimensional vector espaço G 2, mas eles podem ser facilmente aplicada da mesma maneira para os espaços de dimensões superiores.
Homothety, identidade, ponto de reflexão e transformação nula
Como um vetor unidimensional espaço L 1, considere uma seqüência de borracha amarrada ao suporte imóvel em uma extremidade, como a que está em tipóia de uma criança. Puxar a corda para longe do ponto de ligação que se estende e que se alonga por algum factor de escala λ que é um número real. Cada vetor na corda é igualmente alargada, com o mesmo fator de escala λ e, embora alongado ele preserva sua direção original. Este tipo de transformação é chamado homotetia (transformação de similaridade). Para um espaço vectorial bidimensional L2, considerar uma folha de borracha esticada de forma igual em todas as direcções, tal como uma pequena área da superfície de um balão infla (Fig. 3). Todos os vectores de origem num ponto fixo na superfície do balão são esticados igualmente com o mesmo factor de escala λ. A transformação homotetia em duas dimensões é descrito por uma matriz quadrada de 2 × 2, agindo sobre um vector arbitrário no plano da superfície de alongamento / encolhendo. Depois de fazer a multiplicação de matrizes, obtém-se:
que, expresso em palavras, significa que a transformação é equivalente a multiplicar o comprimento do vector por λ preservando ao mesmo tempo a sua orientação original. A equação assim obtida é exactamente a equação valor próprio. Uma vez que o vetor tomada foi arbitrária, em homothety qualquer vector no espaço vetorial sofre a equação de valores próprios, ou seja, qualquer vector que encontra-se na superfície do balão pode ser um vector próprio. Se a transformação é o alongamento (alongamento, a extensão, a inflação), ou encolher (compressão, a deflação) depende do factor de escala: se λ> 1, isto é o alongamento, se λ <1, que está a diminuir.
Várias outras transformações pode ser considerado um tipo especial de homotetia com algum valor fixo, constante de λ: identidade em que deixa inalterada vectores, λ = 1; na reflexão sobre um ponto que preserva comprimento e direção de vetores, mas muda sua orientação para o oposto, λ = -1; e em transformação nulo que transforma cada vector para o vector zero, λ = 0. A transformação nula não dá origem a um vector próprio uma vez que o vector de zero não pode ser um vector próprio mas tem Eigenspace desde autoespaço contém também o vector de zero por definição.
Scaling desigual
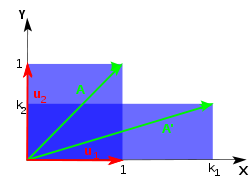
Por exemplo, um pouco mais complicado, considere uma folha que é esticada uneqally em duas direcções perpendiculares, ao longo dos eixos de coordenadas, ou, de modo semelhante, esticada numa direcção, e encolhido no outro sentido. Neste caso, existem dois factores de escala diferentes: k 1 para o dimensionamento na direcção x, e k 2 para o dimensionamento no sentido y. A matriz de transformação é 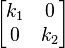 , E a equação é característica λ 2 - λ (k + 1 k 2) k + 1 k = 2 0. Os valores próprios, obtidos como raízes desta equação são λ 1 k = 1, 2 e λ = k 2, que significa, como esperado, os dois valores próprios que são os factores de escala nas duas direcções. Tapar k 1 de volta na equação valor próprio dá um dos vectores próprios:
, E a equação é característica λ 2 - λ (k + 1 k 2) k + 1 k = 2 0. Os valores próprios, obtidos como raízes desta equação são λ 1 k = 1, 2 e λ = k 2, que significa, como esperado, os dois valores próprios que são os factores de escala nas duas direcções. Tapar k 1 de volta na equação valor próprio dá um dos vectores próprios:
Dividindo a última equação por 2 k - k 1, obtém-se y = 0, que representa o eixo x. Um vector com comprimento 1 tomada ao longo deste eixo representa o vector próprio normalizado correspondente ao valor próprio λ 1. O vector próprio correspondente a λ 2, que é um vector de unidade ao longo do eixo Y é encontrada de maneira semelhante. Neste caso, ambos os valores próprios são simples (com algébrica e as multiplicidades geométricas iguais a 1). Dependendo dos valores de λ 1 e λ 2, existem vários casos especiais notáveis. Em particular, se λ 1> 1, e λ 2 = 1, a transformação é um estiramento na direcção do eixo x. Se λ 2 = 0, e λ 1 = 1, a transformação é uma projecção da superfície G 2 sobre o eixo x, porque todos os vectores na direcção de y se tornar zero de vectores.
Deixe a folha de borracha é esticada ao longo do eixo x (k 1> 1) e, simultaneamente, encolhido ao longo do eixo y (k 2 <1) como na Fig. 4. Em seguida, λ 1 = k 1 será o valor próprio diretor. Se aplicar repetidamente essa transformação de alongamento / encolhendo muitas vezes para a folha de borracha irá transformar esta última mais e mais parecido com uma corda de borracha. Qualquer vector na superfície da folha de borracha será orientada cada vez mais perto à direcção do eixo x (da direcção do estiramento), que é, torna-se colinear com o vector próprio responsável principal.
Tosquiar
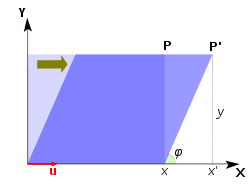
Cisalhamento no plano é uma transformação no qual todos os pontos ao longo de uma dada linha permanecem fixos, enquanto que outros pontos são deslocadas paralelamente a essa linha por uma distância proporcional a sua distância a partir da linha perpendicular. Ao contrário de escala, corte uma figura plana não muda sua área. De cisalhamento pode ser horizontal - ao longo do eixo X, ou vertical - ao longo do eixo Y. No corte horizontal (Fig. 5), um ponto P do avião move-se paralelo ao eixo X para o lugar P ', de modo que a sua coordenada y não se altera enquanto a incrementos para se tornar x coordenada x' = x + k, onde k é chamado fator de cisalhamento. O fator de cisalhamento é proporcional à y e à φ ângulo de corte: k = x '- x = y berço φ. A matriz de uma transformação de cisalhamento é horizontal 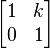 . A equação característica é λ 2-2 λ + 1 = (1 - λ) = 2 0 que tem uma única raiz λ = 1. Portanto, o valor próprio λ = 1 é múltiplo com multiplicidade algébrica 2. O vector próprio (s) são encontrados como soluções de
. A equação característica é λ 2-2 λ + 1 = (1 - λ) = 2 0 que tem uma única raiz λ = 1. Portanto, o valor próprio λ = 1 é múltiplo com multiplicidade algébrica 2. O vector próprio (s) são encontrados como soluções de
A última equação é dividido por k (normalização) para se obter y = 0, que é uma linha recta ao longo do eixo x. Esta linha representa a autoespaço unidimensional. No caso de corte da multiplicidade algébrica dos valores próprios (2) é menor do que a sua multiplicidade geométrica (1, a dimensão da autoespaço). O autovetor é um vetor unitário ao longo do eixo x. O caso de corte vertical com matriz de transformação 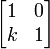 é tratado de uma forma similar; o vector próprio em corte vertical é ao longo do eixo y. Aplicando repetidamente a transformação de corte muda a direcção de qualquer vector no plano mais perto e mais perto da direcção do vector próprio.
é tratado de uma forma similar; o vector próprio em corte vertical é ao longo do eixo y. Aplicando repetidamente a transformação de corte muda a direcção de qualquer vector no plano mais perto e mais perto da direcção do vector próprio.
Rotação
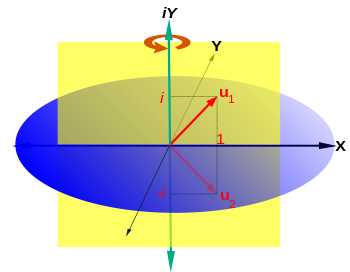
A rotação num plano é uma transformação que descreve o movimento de um corpo rígido (ou vector) em torno de um ponto fixo. Com a ajuda das funções trigonométricas, a rotação pode ser descrito como uma transformação linear. Os elementos de uma matriz de rotação representar os componentes do vector de rotação. Assim, uma rotação anti-horária de coordenadas de vectores, ou um plano sobre a origem a um ângulo φ em que as coordenadas x e y mudança de x 'e y' é descrita pelo seguinte sistema de equações lineares:
ou, em termos de vectores e matrizes de coluna:
A equação característica da matriz de transformação 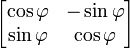 é λ 2 - 2λ cos φ + 1 = 0. Esta equação quadrática tem um discriminante D = 4 (cos φ 2 - 1) = - 4 sin 2 φ que é um número negativo para φ ≠ 0 ° e 180 ° φ ≠ × k com k ímpar. Portanto, exceto para os últimos casos especiais, verdadeiras raízes (autovalores) não existem para rotação. A equação característica tem duas raízes complexas λ 1 e λ 2, que são complexos conjugados entre si:
é λ 2 - 2λ cos φ + 1 = 0. Esta equação quadrática tem um discriminante D = 4 (cos φ 2 - 1) = - 4 sin 2 φ que é um número negativo para φ ≠ 0 ° e 180 ° φ ≠ × k com k ímpar. Portanto, exceto para os últimos casos especiais, verdadeiras raízes (autovalores) não existem para rotação. A equação característica tem duas raízes complexas λ 1 e λ 2, que são complexos conjugados entre si:
Estas duas raízes são os dois valores próprios de rotação, cada um com uma multiplicidade algébrica igual a 1. Tapar o primeiro valor próprio, λ 1, de volta na equação de valor próprio dá o primeiro autovetor:
Outros exemplos
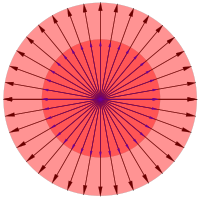
À medida que a Terra gira, cada seta que aponta para fora a partir do centro da Terra gira também, com excepção das setas que são paralelas ao eixo de rotação. Considere a transformação da Terra após uma hora de rotação: Uma seta a partir do centro da Terra ao Geographic Pólo Sul seria um autovetor desta transformação, mas uma seta a partir do centro da Terra para qualquer lugar do equador não seria um vector próprio. Uma vez que a seta a apontar no pólo não é esticado pela rotação da Terra, o seu valor próprio é 1.

No entanto, o espaço geométrico tridimensional não é o único espaço vetorial. Por exemplo, considere uma corda salientou fixado em ambas as extremidades, como as cordas vibrantes de um instrumento de cadeia (Fig. 2). As distâncias de átomos da corda de vibração das suas posições quando a corda é em repouso pode ser visto como os componentes de um vector num espaço com o maior número de dimensões, como não são átomos na corda.
Assuma a corda é um meio contínuo. Se considerarmos a equação para a aceleração em cada ponto da corda, os seus vectores próprios, ou funções próprias , são as ondas estacionárias. As ondas estacionárias correspondem às oscilações particulares da corda de modo a que a aceleração da corda é simplesmente a sua forma escalonado por um factor de este factor, o valor próprio, acaba por ser 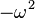 onde
onde 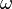 é o frequência angular da oscilação. Cada componente do vector associado com a corda é multiplicada por um factor dependente de tempo de
é o frequência angular da oscilação. Cada componente do vector associado com a corda é multiplicada por um factor dependente de tempo de 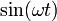 . Se amortecimento é considerada, a amplitude de oscilação diminui esta até que a corda pára oscilante, o que corresponde a um complexo ω. Pode-se então associar um tempo de vida com a parte imaginária de ω, e relacionar o conceito de um vector próprio para o conceito de ressonância. sem amortecimento, o facto de que o operador de aceleração (assumindo uma densidade uniforme) é leva Hermitiana várias propriedades importantes, como o os padrões de ondas permanentes são funções ortogonais.
. Se amortecimento é considerada, a amplitude de oscilação diminui esta até que a corda pára oscilante, o que corresponde a um complexo ω. Pode-se então associar um tempo de vida com a parte imaginária de ω, e relacionar o conceito de um vector próprio para o conceito de ressonância. sem amortecimento, o facto de que o operador de aceleração (assumindo uma densidade uniforme) é leva Hermitiana várias propriedades importantes, como o os padrões de ondas permanentes são funções ortogonais.
Autofunções
No entanto, é por vezes pouco natural ou mesmo impossível para escrever a equação de valores próprios de uma matriz de forma. Isto ocorre, por exemplo, quando o espaço vectorial é infinito dimensional, por exemplo, no caso de a corda acima. Dependendo da natureza da transformação T e o espaço a que se aplica, pode ser vantajoso para representar a equação valor próprio como um conjunto de equações diferenciais . Se T é um operador diferencial, os vectores próprios são comumente chamados de funções próprias do operador diferencial que representam T . Por exemplo, diferenciação em si é uma transformação linear desde
(f(t) eg(t) sãofunções diferenciáveis, eumebsãoconstantes).
Considere diferenciação com relação a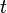 .suas funções própriash(t) obedecem a equação de valores próprios:
.suas funções própriash(t) obedecem a equação de valores próprios:
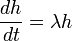 ,
,
onde λ é o valor próprio associado com a função. Tal função do tempo é constante se 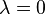 , cresce proporcionalmente a si mesmo se
, cresce proporcionalmente a si mesmo se 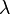 é positivo, e decai proporcionalmente a si mesmo se
é positivo, e decai proporcionalmente a si mesmo se 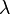 é negativo. Por exemplo, uma população idealizada de coelhos gera mais rápido quanto mais existem coelhos, e, portanto, satisfaz a equação com um lambda positivo.
é negativo. Por exemplo, uma população idealizada de coelhos gera mais rápido quanto mais existem coelhos, e, portanto, satisfaz a equação com um lambda positivo.
A solução para a equação de valores próprios é 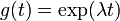 , a função exponencial ; assim que a função é uma função própria do operador diferencial d / dt com o valor próprio λ . Se λ é negativo , chamamos a evolução do g um decaimento exponencial; se for positivo , um crescimento exponencial . O valor de λ pode ser qualquer número complexo . O espectro de d / dt é, por conseguinte, todo o plano complexo . Neste exemplo, o espaço vectorial, em que o operador d / dt actua é o espaço das funções diferenciáveis de uma variável. Este espaço tem uma dimensão infinito (porque não é possível expressar cada função diferenciável como uma combinação linear de um número finito de funções de base). No entanto, o autoespaço associado com um dado valor próprio λ é unidimensional. É o conjunto de todas as funções
, a função exponencial ; assim que a função é uma função própria do operador diferencial d / dt com o valor próprio λ . Se λ é negativo , chamamos a evolução do g um decaimento exponencial; se for positivo , um crescimento exponencial . O valor de λ pode ser qualquer número complexo . O espectro de d / dt é, por conseguinte, todo o plano complexo . Neste exemplo, o espaço vectorial, em que o operador d / dt actua é o espaço das funções diferenciáveis de uma variável. Este espaço tem uma dimensão infinito (porque não é possível expressar cada função diferenciável como uma combinação linear de um número finito de funções de base). No entanto, o autoespaço associado com um dado valor próprio λ é unidimensional. É o conjunto de todas as funções 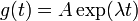 , onde A é uma constante arbitrária, a população inicial em t = 0 .
, onde A é uma constante arbitrária, a população inicial em t = 0 .
Teorema espectral
Na sua versão mais simples, o teorema espectrais que, sob certas condições, uma transformação linear de um vector v pode ser expresso como uma combinação linear dos vectores próprios, no qual o coeficiente de cada vector próprio é igual aos tempos de valores próprios correspondentes do produto escalar (ou produto escalar) do vector próprio com o vector v . Matematicamente, isto pode ser escrito como:
onde v 1 , v 2 , ... e λ 1 , λ 2 , ... representam os autovetores e autovalores de T . O teorema é válido para todas as transformações lineares auto-adjuntos (transformações lineares dadas por reais matrizes simétricas e matrizes hermitianas), e para a classe mais geral de ( complexos ) matrizes normais.
Se alguém define o n -ésimo poder de uma transformação como o resultado de aplicá-la n vezes seguidas, pode-se também definir polinômios de transformações. Uma versão mais geral do teorema é que qualquer polinómio P de T é dado pela
O teorema pode ser alargado a outras funções de transformações, tal comoas funções de análise, o caso mais geral, sendoas funções de Borel.
Eigendecomposition
O teorema espectral para matrizes pode ser demonstrada como segue. Deixe A ser um quadrado n × n matriz. Vamos q 1 ... q k ser uma base eigenvector, ou seja, um conjunto indexado de k autovetores linearmente independentes, onde k é a dimensão do espaço gerado pelos vectores próprios de A . Se k = n , em seguida, um pode ser escrito
ondeQé a praçan×nmatriz cujasi-ésima coluna é a base eigenvectorq EudeAeΛé amatriz diagonal, cuja diagonal elementos são os valores próprios correspondentes, ou seja,Λ ii= λEu.
Espaços de dimensão infinita
Se o espaço é um vector de dimensão infinita espaço de Banach, a noção de valores próprios podem ser generalizados para o conceito de espectro. O espectro é o conjunto de escalares λ para os quais ( T - λ) -1 não está definido; isto é, de tal modo que T - λ não tem inversa limitada.
Claramente, se λ é um autovalor de T , λ está no espectro de t . Em geral, o inverso não é verdadeiro. Há operadores de Hilbert ou de Banach espaços que não têm autovetores em tudo. Isto pode ser visto no exemplo a seguir. O deslocamento bilateral sobre o espaço de Hilbert ℓ 2 ( Z ) (que é, o espaço de todas as sequências de escalares ... um -1 , um 0 , um 1 , um 2 , de tal modo que ...
converge) não tem valor próprio, mas tem valores espectrais.
Em espaços infinitos-dimensional, o espectro de um operador limitado é sempre não vazio. Isto também é verdade para uma ilimitada operador auto adjunto. Via as suas medidas espectrais, o espectro de qualquer operador auto adjunto, delimitadas ou não, pode ser decomposto em absolutamente contínua, ponto puro, e partes singulares. (Ver Decomposição de espectro.)
As funções exponenciais são funções próprias do operador derivado (o derivado de funções exponenciais são proporcionais a eles mesmos). O crescimento exponencial e , por conseguinte, deterioração fornecem exemplos de espectros contínuos, como o faz o exemplo de cadeia de vibração ilustrado acima. O átomo de hidrogénio é um exemplo onde ambos os tipos de espectros aparecer. As funções próprias da Hamiltoniano átomo de hidrogénio são chamados autoestados e são agrupados em duas categorias. O estados ligados ao átomo de hidrogénio de corresponder à parte do espectro discreto (que têm um conjunto discreto de valores próprios que pode ser calculado pela fórmula de Rydberg) enquanto a ionização processos são descritos por a parte contínua (a energia de colisão / ionização não é quantificada).
Aplicações
Equação de Schrödinger

Um exemplo de uma equação onde o valor próprio transformaçãoTé representado em termos de um operador diferencial é independente do tempo daequação Schrödin namecânica quântica:
ondeH, oHamiltoniano, é uma segunda ordemoperador diferencial e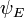 , O função de onda, é uma de suas funções próprias correspondentes ao valor próprioE, interpretadas como a suaenergia.
, O função de onda, é uma de suas funções próprias correspondentes ao valor próprioE, interpretadas como a suaenergia.
No entanto, no caso em que se está interessado apenas nas soluções estado ligado da equação Schrödin, se olha para 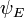 dentro do espaço de funções integráveis quadrados. Uma vez que este espaço é um espaço de Hilbert com uma estrutura bem definida produto escalar, pode-se introduzir uma base fixada no qual
dentro do espaço de funções integráveis quadrados. Uma vez que este espaço é um espaço de Hilbert com uma estrutura bem definida produto escalar, pode-se introduzir uma base fixada no qual 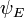 e H pode ser representada como uma matriz unidimensional e uma matriz, respectivamente. Isto permite que se representam a equação Schrödin em forma de matriz. (Fig. 4 apresenta os mais baixos autofunç~oes do átomo de Hidrogénio hamiltoniano.)
e H pode ser representada como uma matriz unidimensional e uma matriz, respectivamente. Isto permite que se representam a equação Schrödin em forma de matriz. (Fig. 4 apresenta os mais baixos autofunç~oes do átomo de Hidrogénio hamiltoniano.)
O Notação de Dirac é frequentemente utilizado neste contexto. Um vector, o que representa um estado do sistema, no espaço de Hilbert de funções integráveis é representado por quadrados 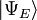 . Nesta notação, a equação é Schrödin:
. Nesta notação, a equação é Schrödin:
onde 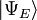 é um auto-estado de H . É um operador auto adjunto, o análogo de dimensão infinita de matrizes hermitianas ( ver Observable ). Tal como no caso da matriz, na equação acima,
é um auto-estado de H . É um operador auto adjunto, o análogo de dimensão infinita de matrizes hermitianas ( ver Observable ). Tal como no caso da matriz, na equação acima, 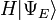 é entendido ser o vector obtido por aplicação da transformação H a
é entendido ser o vector obtido por aplicação da transformação H a 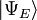 .
.
Orbitais moleculares
Na mecânica quântica , e em particular no atômica e física molecular , dentro da teoria Hartree-Fock, os atômica e orbitais moleculares pode ser definido pelos vectores próprios do operador Fock. Os valores próprios correspondentes são interpretadas como potenciais de ionização via teorema de Koopmans. Neste caso, o vector próprio termo é utilizado num sentido mais geral, um pouco, uma vez que o operador Fock está explicitamente dependente das orbitais e os seus valores próprios. Se alguém quiser sublinhar este aspecto se fala da equação de valores próprios implícita . Tais equações são normalmente resolvidos por um método de iteração, chamado neste caso método de campo auto-consistente. Em química quântica , um muitas vezes representa a equação Hartree-Fock em um não- ortogonal base definida. Esta representação particular, é um problema de valores próprios generalizada chamado equações Roothaan.
Geologia e glaciologia: (Tensor Orientação)
Em geologia , especialmente no estudo de glacial até, vetores e valores eigen são usados como um método pelo qual uma massa de informação de orientação e mergulho 'constituintes de um tecido clastos podem ser resumidos num espaço de 3-D de seis números. No campo, um geólogo pode coletar esses dados para centenas ou milhares de clastos em uma amostra de solo, que só podem ser comparadas graficamente como em um Tri-Plot (Sneed e Folk) diagrama, ou como um Stereonet em um Wulff Net . A saída para o tensor de orientação é em três (perpendiculares) eixos ortogonais de espaço. Autovetores saída de programas como o Stereo32 estão na ordem E1> E2> E3, com E1 sendo a orientação principal de clastos orientação / mergulho, E2 sendo o secundário e E3 sendo o terciário, em termos de força. A orientação clast é definida como a Eigenvector, em uma rosa dos ventos de 360 °. Dip é mensurado como o valor próprio, o módulo do tensor: este é valorizado a partir de 0 ° (não mergulho) e 90 ° (vertical). Vários valores de E1, E2 e E3 significar coisas diferentes, como pode ser visto no livro "Um Guia Prático para o Estudo da Glacial Sedimentos 'por Benn e Evans, 2004.
A análise fatorial
Em análise fatorial, os vectores próprios de uma matriz de covariância ou matriz de correlação correspondem a fatores e valores próprios para a variância explicada por esses fatores. A análise fatorial é uma estatística técnica utilizada nas ciências sociais e na comercialização, gestão de produtos, operações de investigação , e outras ciências aplicadas que lidam com grandes quantidades de dados. O objectivo é explicar a maior parte do covariability entre um número de observáveis variáveis aleatórias em termos de um menor número de variáveis latentes chamados factores não observáveis. As variáveis aleatórias observáveis são modelados como combinações lineares dos factores de desvio, além termos originais. Autovalores são utilizados em análise utilizado pelo software Q-metodologia; factores com valores próprios superiores a 1,00 são considerados significativos, a explicação de uma quantidade importante de a variabilidade dos dados, enquanto valores próprios inferior a 1,00 são considerados demasiado fracos, não explicar uma porção significativa da variabilidade dos dados.
Eigenfaces
Em processamento de imagem, as imagens processadas de faces podem ser vistos como vectores cujos componentes são os brilhos de cada pixel. A dimensão deste espaço vectorial é o número de pixels. Os autovetores da matriz de covariância associada a um grande conjunto de imagens de rostos normalizados são chamados eigenfaces; este é um exemplo de análise de componentes principais. Eles são muito úteis para a expressão de qualquer imagem do rosto como uma combinação linear de alguns deles. No ramo de reconhecimento facial de biometria, eigenfaces fornecer um meio de aplicação de compressão de dados para rostos para fins de identificação. Pesquisa relacionada a sistemas de visão eigen determinantes gestos com as mãos também foi feita. Mais informações sobre a determinação letras de língua gestual usando eigen sistemas pode ser encontrada aqui: http://www.geigel.com/signlanguage/index.php
Semelhante a este conceito, autovozes conceito também é desenvolvido que representa a direção geral da variabilidade na pronúncias humanos de uma declaração particular, como uma palavra em uma língua. Com base em uma combinação linear de tais autovozes, uma nova voz pronúncia da palavra pode ser construído. Estes conceitos foram encontrados útil em sistemas de reconhecimento de voz automático, para adaptação ao locutor.
Tensor de inércia
Em mecânica, os vectores eigen dotensor de inércia definir oseixos principais de umcorpo rígido. O tensor de inércia é uma quantidade necessária de chave, a fim de determinar a rotação de um corpo rígido em torno do seucentro de massa.
Estresse tensor
Em mecânica dos sólidos, o tensor é simétrico e por isso pode ser decomposto em um tensor diagonal com os autovalores na diagonal e vectores próprios como base. Porque é diagonal, nesta orientação, o tensor de tensões não tem componentes de cisalhamento; os componentes que ele tem são os componentes principais.
Valores próprios de um gráfico
Em teoria dos grafos espectral, um valor próprio de um gráfico é definido como um valor próprio de do gráfico matriz de adjacência A , ou (cada vez mais) de do gráfico matriz Laplacian, que é ou T - Um ou I - T 1/2 AT -1/2 , onde T é uma holding matriz diagonal o grau de cada vértice, e em T -1/2 , 0 é substituído por 0 -1/2 . O k th eigenvetor principal de um gráfico é definida como o vector próprio correspondente ao k th maior valor próprio de um , ou o vector próprio correspondente ao k th menor valor próprio do Laplaciano. O primeiro eigenvetor principal do gráfico também é referido apenas como o vector próprio diretor.
O principal vector próprio é usado para medir a centralidade de seus vértices. Um exemplo é o Google 's algoritmo PageRank. O principal vector próprio de um modificado matriz de adjacência do grafo World Wide Web dá às fileiras de página como seus componentes. Este vector corresponde à distribuição estacionária da cadeia de Markov representado pela matriz de adjacência normalizada-linha; no entanto, a matriz de adjacência deve primeiro ser modificado para assegurar a existência de uma distribuição estacionária. O segundo vector próprio diretor pode ser usado para particionar o gráfico em clusters, via agrupamento espectral. Outros métodos também estão disponíveis para o agrupamento.

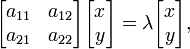
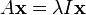
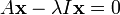
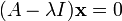
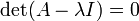
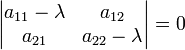
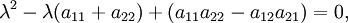
![\ Lambda_ {1,2} = \ frac {1} {2} \ left [(a_ {11} + {22} a_) \ pm \ sqrt {{12} 4a_ a_ {21} + (a_ {11} - a_ {22}) ^ 2} \ right].](../../images/149/14952.png)