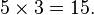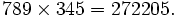Aritmética elementar
Sobre este escolas selecção Wikipedia
Crianças SOS, que corre cerca de 200 sos escolas no mundo em desenvolvimento, organizado esta selecção. Uma boa maneira de ajudar outras crianças é por patrocinar uma criança
Aritmética elementar é o tipo mais básico de matemática : trata-se das operações de adição , subtração , multiplicação e divisão . A maioria das pessoas aprender elementar aritmética em ensino fundamental.
Aritmética elementar começa com os números naturais e os algarismos arábicos usados para representá-los. Ele requer a memorização de tabelas de adição e tabuada para adicionar e multiplicando pares de dígitos. Sabendo dessas tabelas, uma pessoa pode executar certos procedimentos conhecidos para a adição e multiplicação números naturais. Outros algoritmos são utilizados para subtração e divisão aritmético mental aritmética elementar é realizada na cabeça, por exemplo, para saber que 100 -. 37 = 63, sem utilização de papel. É uma habilidade todos os dias. Formas estendidas de cálculo mental podem envolver calcular números extremamente grandes, mas esta é uma habilidade geralmente não ensinou ao nível elementar.
Aritmética elementar passa então a frações , decimais e números negativos , que podem ser representados em um linha número.
Hoje em dia as pessoas usam rotineiramente eletrônicos calculadoras , caixas registadoras, e computadores para executar sua aritmética elementar para eles. Mais cedo cálculo ferramentas incluídas réguas de cálculo (por multiplicação, divisão, logs e trig), tábuas de logaritmos , nomogramas, e calculadoras mecânicas.
A questão da existência ou não calculadoras deve ser usada, e se métodos de cálculo manuais de matemática tradicionais ainda devem ser ensinados na escola primária tem provocado polêmica como muitos textos de matemática com base em padrões deliberadamente omitir alguns ou mais padrão de métodos de cálculo. A 1989 Normas NCTM levou a currículos que os métodos de cálculo não-padrão-de enfatizada ou omitida muito do que foi considerado aritmética elementar na escola primária, e substituiu-o com ênfase em temas tradicionalmente estudados na faculdade, como álgebra, estatísticas e resolução de problemas, e desconhecido para a maioria dos adultos.
Nos tempos antigos, o ábaco foi usado para executar a aritmética elementar, e ainda é em muitas partes da Ásia. Um usuário experiente pode ser tão rápido com um ábaco como com uma calculadora, que pode exigir baterias.
No século 14 algarismos arábicos foram introduzidos na Europa pelos Leonardo Pisano. Estes números foram mais eficientes para a realização de cálculos do que numerais romanos , por causa do sistema de posicionamento.
Os dígitos
0, de zero , representa ausência de objectos a serem contadas.
1, um . Esta é uma vara: I
2, dois. Esta é duas varas: II
3, três. Esta é três varas: III
4, quatro. Este é de quatro varas: II I I
5, cinco. Este é cinco varas: II I II
6, seis. Este é de seis varas: II I III
7, Sete. Este é sete varas: II I II I I
8, oito. Este é oito varas: II I II I II
9, nove. Este é nove varas: II I II I III
Há quantos dígitos como dedos nas mãos: a palavra "dígitos" também pode significar dedo. Mas se a contagem dos dígitos em ambas as mãos, o primeiro dígito seria um eo último dígito não seria contado como "zero", mas como " dez ":.. 10, composta pelos algarismos um e zero O número 10 é o primeiro número de dois dígitos Este é dez varas: II I II I II II
Se um número tiver mais de um dígito, então o dígito mais à direita, que dizem ser o último dígito, é chamado de "os dígitos". O dígito imediatamente à sua esquerda é a "dezenas dígitos". O dígito imediatamente à esquerda do dezenas dígitos é o "centenas dígitos". O dígito imediatamente à esquerda do centenas dígitos é a "milhares dígitos".
Adição
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
O que significa para somar dois números naturais? Suponha que você tenha dois sacos, um saco segurando cinco maçãs e um segundo saco segurando três maçãs. Agarrando um terceiro, o saco vazio, mover todas as maçãs das primeira e segunda bolsas para o terceiro saco. A terceira bolsa passou a deter oito maçãs. Isto ilustra a combinação de três e cinco maçãs Maçãs é oito maçãs; ou de modo mais geral: "três mais cinco são oito" ou "três mais cinco é igual a oito" ou "oito é a soma de três e cinco". Os números são resumo, e a adição de um grupo de três coisas a um grupo de cinco coisas irá produzir um grupo de oito coisas. Além é um reagrupamento: dois conjuntos de objetos que foram contados separadamente são colocados em um único grupo e contou juntos: a contagem do novo grupo é a "soma" das contagens separadas dos dois grupos originais.
Simbolicamente, a adição é representada pela " sinal de mais ":. + Assim, a declaração" três mais cinco é igual a oito "pode ser escrito simbolicamente como 3 + 5 = 8. A ordem em que dois números são somados, não importa, assim 3 + 5 = 5 + 3 = 8. Este é o conmutativo propriedade de adição.
Para adicionar um par de dígitos utilizando a tabela, encontrar a intersecção da linha do primeiro dígito com a coluna do segundo dígito: da linha e da coluna intersectam-se um quadrado contendo a soma dos dois dígitos. Alguns pares de dígitos adicionar-se aos números de dois dígitos, com a dezenas dígitos sempre sendo um 1. No algoritmo adição a dezenas dígitos da soma de um par de dígitos é o chamado " realizar dígito ".
Algoritmo de adição
Para simplificar, considere apenas os números com três dígitos ou menos. Para adicionar um par de números (escrito em algarismos arábicos), escrever o segundo número sob o primeiro, de modo que os dígitos alinham em colunas: a coluna mais à direita irá conter o os dígitos do segundo número sob o ones dígitos do primeiro número. Esta coluna mais à direita é o ones-coluna. A coluna imediatamente à sua esquerda é a dezenas-coluna. As dezenas coluna terá a dezenas dígitos do segundo número (se tiver um) segundo a dezenas dígitos do primeiro número (se tiver um). A coluna imediatamente à esquerda da coluna é dezenas a centenas-coluna. A coluna de centenas vai alinhar a centenas dígitos do segundo número (se houver um) segundo a centenas dígitos do primeiro número (se houver).
Após o segundo número foi escrito para baixo sob o primeiro dígitos para que se alinham em suas colunas corretas, desenhar uma linha sob o segundo (parte inferior) número. Comece com os de coluna: os de coluna deve possuir um par de dígitos: o ones dígitos do primeiro número e, sob ele, os dígitos do segundo número. Encontre a soma destes dois dígitos: escrever esta soma sob a linha e no ones-coluna. Se a soma tem dois dígitos, em seguida, anote apenas os dígitos da soma. Faça o "dígitos transportar" acima do topo dígitos da coluna seguinte: neste caso, a coluna seguinte, é a dezenas-coluna, de modo a escrever uma acima da dezenas dígitos do primeiro número.
Se ambos os primeiro e segundo número de cada um tem apenas um dígito, em seguida, a sua soma é dado na tabela a adição, e o algoritmo de adição é desnecessária.
Em seguida, vem a dezenas coluna. As dezenas-coluna pode conter dois dígitos: a dezenas dígitos do primeiro número e as dezenas dígitos do segundo número. Se um dos números tem uma falta dezenas dígitos, em seguida, a dezenas dígitos para este número pode ser considerado como um zero. Adicione as dezenas dígitos dos dois números. Então, se não houver um dígito carry, adicioná-lo a esta soma. Se a soma foi de 18, em seguida, adicionando o dígito de transporte a ela irá produzir 19. Se a soma das dezenas dígitos (transportar mais dígitos, se houver um) é inferior a dez, em seguida, gravar na dezenas-coluna abaixo da linha. Se a soma tem dois dígitos, em seguida, escrever o último dígito na dezenas coluna sob a linha, e realizar seu primeiro dígito (que deve ser um um) para a próxima coluna: neste caso a coluna de centenas de pessoas.
Se nenhum dos dois números tem uma centenas dígitos, em seguida, se não houver um dígito de transporte, em seguida, o algoritmo de completada a adição. Se não houver um dígito carry (transitadas do dezenas-coluna), em seguida, escreva-o no-centenas coluna sob a linha, eo algoritmo é terminado. Quando o algoritmo termina, o número abaixo da linha é a soma dos dois números.
Se pelo menos um dos números tem uma centenas dígitos, em seguida, se um dos números tem uma falta centenas dígitos, em seguida, escrever um dígito zero em seu lugar. Adicione as duas centenas de dígitos, e sua soma adicionar o dígito carry se houver. Em seguida, escreva a soma das centenas coluna abaixo da linha, também na coluna centenas. Se a soma tem dois dígitos, em seguida, anote o último dígito da soma na coluna centenas e escrever o dígito carry à sua esquerda: por milhares colunas.
Exemplo
Diga se quer encontrar a soma dos números 653 e 274. Faça o segundo número no âmbito do primeiro, com algarismos alinhados em colunas, assim:
| 6 | 5 | 3 |
| 2 | 7 | 4 |
Em seguida, desenhe uma linha sob o segundo número e começar com os de coluna. O ones dígitos do primeiro número é 3 e do segundo número é 4. A soma de três e quatro são sete, então escrever uma das sete da queridos coluna sob a linha:
| 6 | 5 | 3 |
| 2 | 7 | 4 |
| 7 |
Em seguida, a dezenas-coluna. As dezenas dígitos do primeiro número é 5, e as dezenas dígitos do segundo número é 7, e cinco mais sete é doze: 12, que tem dois dígitos, então escrever o último dígito, 2, na coluna de dezenas- abaixo da linha, e escrever o dígito carry sobre a centenas coluna acima do primeiro número:
| 1 | ||
| 6 | 5 | 3 |
| 2 | 7 | 4 |
| 2 | 7 |
Em seguida, a centenas colunas. A centenas dígitos do primeiro número é 6, enquanto a centenas dígitos do segundo número é 2. A soma de seis e dois é oito, mas há um dígito carry, que somados aos oito é igual a nove. Faça a nove sob a linha no centenas coluna:
| 1 | ||
| 6 | 5 | 3 |
| 2 | 7 | 4 |
| 9 | 2 | 7 |
Sem dígitos (sem colunas) e foram deixadas unadded, então o algoritmo termina, e
- 653 + 274 = 927.
Sucessão e tamanho
O resultado da adição de um de um número é o sucessor desse número. Exemplos:
o sucessor de zero é um,
o sucessor de um é dois,
o sucessor de dois é três,
o sucessor de dez é onze.
Todo número natural tem um sucessor.
O antecessor do sucessor de um número é o número em si. Por exemplo, cinco é o sucessor de quatro, portanto, quatro é o antecessor de cinco. Cada número natural com excepção do zero tem um predecessor.
Se um número é o sucessor de um outro número, então o primeiro número é dito para ser maior do que o outro número. Se um número é maior que um outro número, e se a outra número é maior do que um terceiro número, então o primeiro número é também maior do que o terceiro número. Exemplo: cinco é maior do que quatro, e quatro é maior do que três, cinco, por conseguinte, é maior do que três. Mas seis é maior do que cinco, seis, portanto, também é maior do que três. Mas sete é maior do que seis, sete, portanto, também é maior do que três ..., portanto, oito é maior do que três ..., portanto, nove é maior do que três, etc.
Se dois números naturais diferentes de zero são adicionadas em conjunto, em seguida, a sua soma é maior do que qualquer um deles. Exemplo: três mais cinco é igual a oito, oito, portanto, é maior do que três (8> 3) e oito é maior do que cinco (8> 5). O símbolo de "maior que" é>.
Se um número é maior do que a outra, então o outro é menor do que o primeiro. Exemplos: três é menor do que oito (3 <8) e cinco é menor do que oito (5 <8). O símbolo para menor do que é <. Um número não podem ser ao mesmo tempo maior e menor do que outro número. Nem um número pode ser ao mesmo tempo maior do que e igual a um outro número. Dado um par de números naturais, um e somente um dos seguintes casos devem ser verdadeiras:
- o primeiro número é maior do que o segundo,
- o primeiro número é igual ao segundo,
- o primeiro número é menor do que o segundo.
Contando
Para contar um grupo de objectos meios para atribuir um número natural de cada um dos objectos, como se fosse um selo para esse objecto, de tal modo que um número natural nunca é atribuída a um objecto, a menos que o seu antecessor já foi atribuído a um outro objecto, com a excepção de que zero não é atribuído a qualquer objecto: o menor número natural a ser atribuído é um, e o maior número natural atribuído depende do tamanho do grupo. Chama-se a contagem e é igual ao número de objectos em que grupo.
O processo de contando um grupo, é a seguinte:
Passo 1: Deixe "contagem" ser igual a zero. "A contagem" é uma quantidade variável, que embora começando com um valor de zero, logo tem o seu valor mudado várias vezes.
Passo 2: Encontre pelo menos um objeto no grupo que não tenha sido marcado com um número natural. Se nenhum objeto pode ser encontrado (se todas elas foram rotulados), em seguida, a contagem estiver concluída. Caso contrário, escolha um dos objetos não marcados.
Passo 3: aumentar a contagem por um. Isto é, substituir o valor da contagem pelo seu sucessor.
Passo 4: atribuir o novo valor de contagem, como uma etiqueta, para o objecto não marcado escolhido no Passo 2.
Passo 5: Volte para a Etapa 2.
Quando a contagem estiver concluída, o último valor de contagem será a contagem final. Esta contagem é igual ao número de objectos no grupo.
Muitas vezes, quando se contam objectos, não se manter a par do que rótulo numérico corresponde a qual objeto: só mantém o controle do subgrupo de objetos que já foram rotulados, de forma a ser capaz de identificar objetos não marcados necessário para Etapa 2. Todavia , se um está contando as pessoas, então pode-se pedir às pessoas que estão sendo contados para cada manter o controle do número que foi atribuído auto da pessoa. Após a contagem terminar, é possível pedir ao grupo de pessoas para arquivar-se em uma linha, em ordem crescente de etiqueta numérica. O que as pessoas fariam durante o processo de alinhar seria algo como isto: cada par de pessoas que não tem certeza de suas posições na linha de pedir uns aos outros o que seus números são: a pessoa cujo número é menor deve ficar do lado esquerdo e aquele com o maior número no lado direito da outra pessoa. Assim, pares de pessoas comparar seus números e suas posições, e comutar as suas posições conforme necessário, e através da repetição de tais comutações condicionais tornam-se solicitados.
Algoritmos para Subtração
Existem vários métodos para realizar subtracção. Matemática tradicional ensinado crianças do ensino fundamental para subtrair utilizando métodos adequados para o cálculo de mão. O método particular utilizado varia de país de país, e dentro de um país, os métodos diferentes estão na moda em tempos diferentes. Matemática baseada em padrões distinguem-se geralmente pela falta de preferência por qualquer método padrão, substituído por orientação das crianças segundo grau de inventar seus próprios métodos de cálculo, como o uso de propriedades de números negativos no caso de TERC.
Escolas americanas ensinam actualmente um método de subtração usando empréstimos e um sistema de marcações chamado muletas. Embora um método de empréstimo tinha sido conhecido e publicado em livros anteriores, aparentemente, as muletas são a invenção de William A. Browell que os utilizados em um estudo em Novembro de 1937 . Este sistema pegou rapidamente, deslocando os outros métodos de subtracção em uso nos Estados Unidos nesse tempo.
Crianças europeias são ensinados, e alguns mais velhos americanos empregam, um método de subtracção do chamado método austríaco, também conhecido como o método de adições. Não há nenhuma contracção neste método. Há também muletas (marcações para ajudar a memória) que [provavelmente] variam consoante o país.
No método da contracção de empréstimos, uma subtração, como 86-39 irá realizar a subtração de um lugar de 9 a partir de 6 por empréstimo a 10 de 80 e adicionando-o ao 6. O problema é, assim, transformado em (70 + 16) -39, eficazmente. Isto é indicado pela remoção através do 8, escrevendo um pequeno 7 acima dela, e escrevendo uma pequena 1 acima a 6. Estas marcações são chamados de muletas. A 9 é então subtraído a partir de 16, deixando 7, e 30 a partir do 70, deixando 40, ou 47 como o resultado.
No método de adições, um 10 é pedido para fazer a 6 em 16, em preparação para a subtracção de 9, tal como no método de contracção. No entanto, o 10 não foi obtido por redução minuendo, em vez aumenta a uma subtraendo. Com efeito, o problema é transformado em (80 + 16) - (39 + 10). Tipicamente uma muleta de um pequeno é marcado apenas abaixo do dígito subtraendo como um lembrete. Em seguida, as operações de proceder: 9 a partir de 16 é 7; e 40 (isto é, 30 + 10) a partir de 80 a 40, ou 47 como o resultado.
O método de adições parecem ser ensinado em duas variações, que diferem apenas em psicologia. Continuando o exemplo de 86-39, a primeira variação tenta subtrair 9 de 6, 9 e depois de 16, emprestando a 10 por marcação perto do dígito do subtraendo na próxima coluna. A segunda variação tenta encontrar um dígito que, quando adicionado a 9 dá 6, e reconhecendo que não é possível, dá 16, e transportando o 10 do 16 como uma marcação perto do mesmo dígito como no primeiro método um. As marcações são os mesmos, é apenas uma questão de preferência a respeito de como uma explica sua aparência.
Como precaução final, o método de endividamento fica um pouco complicado em casos como 100-87, onde um empréstimo não pode ser feita imediatamente, e deve ser obtido por chegar através de várias colunas. Neste caso, o minuendo é efetivamente reescrito como 90 + 10, tomando um cem das centenas, fazendo dez dezenas partir dele, e imediatamente pedir o que até nove dezenas na coluna dezenas e, finalmente, colocar um dez na coluna da uma .
Existem vários outros métodos, alguns dos quais são particularmente vantajoso para o cálculo da máquina. Por exemplo, os computadores digitais empregam o método de complemento de dois. De grande importância é o método contando-se por que a mudança é feita. Suponha que uma quantidade P é dado a pagar o montante exigido Q, com P maior do que Q. Em vez de realizar o PQ subtração e contando essa quantia em mudança, o dinheiro é contado a partir de Q e continuando até chegar P. Curiosamente, embora o montante contado para fora deve ser igual ao resultado do PQ subtração, a subtração nunca foi realmente feito e o valor de PQ pode ainda ser desconhecido para a mudança-maker.
1 Subtração nos Estados Unidos: Uma Perspectiva Historial, Susan Ross, Mary Pratt-Cotter, o educador Matemática, Vol. 8, No. 1.
Browell, WA (1939). Aprender como a reorganização: Um estudo experimental em aritmética da terceira série, Duke University Press.
Veja também:
- Método de complementos
- Subtração sem empréstimo
Multiplicação
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
Quando dois números são multiplicados juntos, o resultado é um produto chamado. Os dois números multiplicados juntos são chamados de fatores.
O que significa para multiplicar dois números naturais? Suponha que há cinco sacos vermelhos, cada um contendo três maçãs. Agora agarrar um saco verde vazio, mover todas as maçãs de todos os cinco sacos vermelhos no saco verde. Agora o saco verde terá quinze maçãs. Assim, o produto de cinco e três é quinze. Isso também pode ser indicado como "cinco vezes três é quinze" ou "cinco vezes três é igual a quinze" ou "quinze é o produto de cinco e três". A multiplicação pode ser visto como uma forma de adição repetida: o primeiro factor indica quantas vezes o segundo factor deve ser adicionado em si mesmo; a soma final que é o produto.
Simbolicamente, a multiplicação é representada pelo sinal de multiplicação: 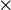 . Assim, a declaração "cinco vezes três é igual a quinze" pode ser escrito simbolicamente como
. Assim, a declaração "cinco vezes três é igual a quinze" pode ser escrito simbolicamente como
Em alguns países, e na aritmética mais avançado, outros sinais de multiplicação são usados, por exemplo, 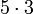 . Em algumas situações, especialmente em álgebra , onde os números podem ser simbolizado com letras, o símbolo de multiplicação pode ser omitida; por exemplo,
. Em algumas situações, especialmente em álgebra , onde os números podem ser simbolizado com letras, o símbolo de multiplicação pode ser omitida; por exemplo, 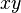 meio
meio 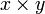 . A ordem em que os dois números são multiplicados não importa, de modo que, por exemplo, três vezes quatro é igual a quatro vezes três. Esta é a propriedade comutativa da multiplicação.
. A ordem em que os dois números são multiplicados não importa, de modo que, por exemplo, três vezes quatro é igual a quatro vezes três. Esta é a propriedade comutativa da multiplicação.
Para multiplicar um par de dígitos utilizando a tabela, encontrar a intersecção da linha do primeiro dígito com a coluna do segundo dígito: da linha e da coluna intersectam-se um quadrado contendo o produto dos dois dígitos. A maioria dos pares de dígitos produzir números de dois dígitos. No algoritmo de multiplicação a dezenas dígitos do produto de um par de dígitos é o chamado " realizar dígito ".
Algoritmo de multiplicação de um fator único dígito
Considere-se uma multiplicação onde um dos factores tem apenas um dígito, enquanto que o outro factor tem uma quantidade arbitrária de dígitos. Anote o fator de vários dígitos, em seguida, escrever o fator de um dígito sob o último dígito do fator de vários dígitos. Desenhe uma linha horizontal sob o fator único dígito. Daí em diante, o fator de um dígito será chamado o "multiplicador" eo fator multi-dígito será chamado de "multiplicando".
Suponha, por simplicidade que o multiplicando tem três dígitos. O primeiro dígito é a centenas dígitos, o dígito do meio é a dezenas dígitos, ea última, mais à direita, dígito é o ones dígitos. O multiplicador só tem um queridos dígitos. Os de dígitos do multiplicando e multiplicador formar uma coluna: os de coluna.
Comece com os de coluna: os de coluna deve possuir um par de dígitos: o ones dígitos do multiplicando e, sob ele, os dígitos do multiplicador. Encontre o produto destes dois dígitos: escrever este produto sob a linha e no ones-coluna. Se o produto tem dois dígitos, em seguida, anote apenas os dígitos do produto. Faça o "dígitos transportar" como um sobrescrito do dígito Ainda-não escrita na coluna seguinte e abaixo da linha: neste caso, a coluna seguinte, é a dezenas-coluna, de modo a escrever dígitos de transporte como o expoente das dezenas ainda não escritas- quatro dígitos do produto (abaixo da linha).
Se ambos primeiro e segundo número cada um tem apenas um dígito, em seguida, seu produto é dada na tabela de multiplicação, eo algoritmo de multiplicação é desnecessário.
Em seguida, vem a dezenas coluna. As dezenas coluna até agora contém apenas um dígito: a dezenas dígitos do multiplicando (embora possa conter um dígito carry abaixo da linha). Localize o produto do multiplicador e as dezenas dígitos do multiplicando. Então, se não é um dígito de transporte (sobrescrito, sob a linha e na coluna dezenas-), adicioná-lo a este produto. Se a soma resultante é inferior a dez, em seguida, escrevê-lo na dezenas coluna sob a linha. Se a soma tem dois dígitos, em seguida, escrever o último dígito na dezenas coluna sob a linha, e realizar seu primeiro dígito para a próxima coluna: neste caso a coluna de centenas de pessoas.
Se o multiplicando não tem um centenas dígitos, em seguida, se não houver um dígito de transporte, em seguida, o algoritmo de multiplicação tenha terminado. Se não houver um dígito carry (transitadas do dezenas-coluna), em seguida, escreva-o no-centenas coluna sob a linha, eo algoritmo é terminado. Quando o algoritmo termina, o número abaixo da linha é o produto de dois números.
Se o multiplicando tem uma centenas dígitos ... encontrar o produto do multiplicador eo centenas dígitos do multiplicando, e para este produto adicionar o dígito carry se houver. Em seguida, escreva a soma resultante do centenas coluna abaixo da linha, também na coluna centenas. Se a soma tem dois dígitos, em seguida, anote o último dígito da soma na coluna centenas e escrever o dígito carry à sua esquerda: por milhares colunas.
Exemplo
Diga se quer encontrar o produto dos números 3 e 729. Faça o multiplicador de um dígito sob o multiplicando vários dígitos, com o multiplicador sob a uns dígitos do multiplicando, assim:
| 7 | 2 | 9 |
| 3 |
Em seguida, desenhe uma linha sob o multiplicador e começar com os de coluna. O ones dígitos do multiplicando é 9 eo multiplicador é 3. O produto de três e nove é 27, então escrever uma das sete da queridos coluna sob a linha, e escrever o carry dígitos 2 como um expoente do ainda -unwritten dezenas dígitos do produto sob a linha:
| 7 | 2 | 9 |
| _ | _ | 3 |
| 2 | 7 |
Em seguida, a dezenas-coluna. As dezenas dígitos do multiplicando é 2, o multiplicador é 3, e três vezes dois é seis. Adicione o carry dígitos, 2, para o produto 6 para obter 8. Oito tem apenas um dígito: não carry dígitos, então escrever em dezenas coluna sob a linha:
| 7 | 2 | 9 |
| _ | _ | 3 |
| 2 8 | 7 |
Em seguida, a centenas colunas. A centenas dígitos do multiplicando é 7, enquanto o multiplicador é 3. O produto de três e sete é 21, e não há carry-dígito anterior (transitadas do dezenas-coluna). O produto 21 tem dois dígitos: escrever o último dígito no centenas coluna sob a linha, em seguida, realizar o seu primeiro dígito até a milhares colunas. Desde o multiplicando não tem milhares dígitos, em seguida, escrever este carry dígitos na milhares coluna abaixo da linha (não expoente):
| 7 | 2 | 9 | |
| _ | _ | _ | 3 |
| 2 | 1 | 2 8 | 7 |
Sem dígitos do multiplicando foram deixadas não multiplicado, de modo que o algoritmo termina, e
.
Algoritmo de multiplicação de fatores de vários dígitos
Dado um par de fatores, cada um com dois ou mais dígitos, escreva ambos os fatores para baixo, um sob o outro, de modo que os dígitos alinham em colunas.
Para simplificar considerar um par de números de três dígitos. Faça o último dígito do segundo número com o último dígito do primeiro número, formando a os de coluna. Imediatamente à esquerda da coluna aqueles-será a dezenas-coluna: o topo desta coluna terá o segundo dígito do primeiro número, e abaixo dele será o segundo dígito do segundo número. Imediatamente à esquerda da coluna dezenas-será a centenas-coluna: o topo desta coluna terá o primeiro dígito do primeiro número e por baixo será o primeiro dígito do segundo número. Depois de ter escrito para baixo ambos os fatores, desenhar uma linha sob o segundo fator.
A multiplicação será composto de duas partes. A primeira parte será composta de várias multiplicações envolvendo multiplicadores de um dígito. O funcionamento de cada uma dessas multiplicações já foi descrito no algoritmo de multiplicação anterior, de modo que este algoritmo não irá descrever cada um individualmente, mas só irá descrever como as várias multiplicações com multiplicadores de um dígito deve ser coordenada. A segunda parte irá somar todos os subprodutos da primeira parte, ea soma resultante será o produto.
Primeira parte. Deixe o primeiro fator ser chamado o multiplicando. Que cada dígito do segundo fator ser chamado de multiplicador. Que os dígitos do segundo fator ser chamado de "queridos-multiplicador". Deixe a dezenas dígitos do segundo fator de ser chamado de "dezenas multiplicador". Deixe a centenas dígitos do segundo fator de ser chamado de "centenas multiplicador".
Comece com os de coluna. Localize o produto do ones-multiplicador e multiplicando e anotá-la em uma linha sob a linha, alinhando os dígitos do produto nas colunas previamente definidos. Se o produto tem quatro dígitos, em seguida, o primeiro dígito será o início do milhares-coluna. Deixe este produto ser chamado de "queridos-fila".
Em seguida, a dezenas-coluna. Encontre o produto das dezenas multiplicador e multiplicando e anotá-la em uma fila - chamá-lo de "dezenas-row" - sob o ones-linha, mas deslocou uma coluna para a esquerda. Ou seja, o ones dígitos das dezenas-linha será na dezenas-coluna do queridos carreiras; a dezenas dígitos das dezenas-fila estará sob a centenas dígitos do queridos carreiras; a centenas dígitos das dezenas-fila estará sob a milhares dígitos do ones-linha. Se a dezenas-linha tem quatro dígitos, em seguida, o primeiro dígito será o início do dez milhares colunas.
Em seguida, a centenas colunas. Localize o produto do centenas multiplicador e multiplicando e anotá-la em uma fila - chamá-lo de "centenas-row" - sob a dezenas-linha, mas mudou mais uma coluna para a esquerda. Ou seja, o ones dígitos do centenas-linha será no centenas coluna; a dezenas dígitos do centenas-linha será na milhares coluna; a centenas dígitos do centenas-linha será no dez milhares colunas. Se a centenas-linha tem quatro dígitos, em seguida, o primeiro dígito será o início da centena de-milhares-coluna.
Depois de ter pressionado o ones-row, row-dezenas e centenas carreiras, desenhar uma linha horizontal sob a centenas linha. As multiplicações são mais.
Segunda parte. Agora, a multiplicação tem um par de linhas. O primeiro sob o par de elementos, e o segundo de acordo com as três linhas de subprodutos. Sob a segunda linha haverá seis colunas, que da direita para a esquerda são as seguintes: as colunas, dezenas de coluna, centenas de coluna, milhares de coluna, dez milhares de coluna, e centenas de milhares-coluna.
Entre a primeira ea segunda linhas, os de coluna irá conter apenas um dígito, localizado no queridos-fila: é o ones dígitos do ones-linha. Copie este dígito, reescrevendo-a no queridos-coluna abaixo da segunda linha.
Entre a primeira ea segunda linhas, a dezenas coluna irá conter um par de dígitos localizados na queridos-linha e as dezenas-fila: as dezenas dígitos do ones-fila e os dígitos das dezenas linha. Adicione esses dígitos para cima e se a soma tem apenas um dígito, em seguida, escrever este dígito na dezenas coluna sob a segunda linha. Se a soma tem dois dígitos, em seguida, o primeiro dígito é um carry dígitos: escrever o último dígito para baixo na dezenas coluna sob a segunda linha e levar o primeiro dígito até a centenas colunas, escrevê-lo como um expoente para o ainda -unwritten centenas dígitos no âmbito da segunda linha.
Entre a primeira ea segunda linhas, a centenas coluna irá conter três algarismos: a centenas dígitos do ones-linha, a dezenas dígitos das dezenas-fila, e os dígitos do centenas linha. Encontre a soma desses três dígitos, em seguida, se há um carry-dígitos do dezenas-coluna (escrita em sobrescrito no âmbito da segunda linha na coluna centenas), em seguida, adicione carry dígitos também. Se a soma resultante tem um dígito depois escrevê-la no âmbito da segunda linha na coluna centenas; se ele tem dois dígitos, em seguida, escrever o último dígito para baixo sob a linha no centenas colunas, e levar em relação ao primeiro dígito à milhares colunas, escrevê-lo como um expoente para o ainda-não-escrita milhares dígitos sob a linha.
Entre a primeira ea segunda linhas, a milhares coluna conterá dois ou três dígitos: a centenas dígitos das dezenas-linha, as dezenas dígitos do centenas carreiras, e (possivelmente) a milhares dígitos dos mais -ROW. Encontre a soma destes números, em seguida, se há um carry-dígitos do centenas coluna (escrito em sobrescrito no âmbito da segunda linha na coluna milhares), em seguida, adicione carry dígitos também. Se a soma resultante tem um dígito depois escrevê-la no âmbito da segunda linha na coluna milhares; se ele tem dois dígitos, em seguida, escrever o último dígito para baixo sob a linha na milhares colunas, e realizar o primeiro dígito até a dez milhares colunas, escrevê-lo como um expoente para o ainda-não-escrita de dez milhares dígitos sob a linha.
Entre a primeira ea segunda linhas, a dez milhares coluna irá conter um ou dois dígitos: a centenas dígitos do centenas coluna e (possivelmente) a milhares dígitos das dezenas coluna. Encontre a soma destes dígitos (se a um no-dezenas linha está faltando Pense nisso como um zero), e se há um carry-dígitos do milhares coluna (escrito em sobrescrito no âmbito da segunda linha na ten- milhares de coluna), em seguida, adicione carry dígitos também. Se a soma resultante tem um dígito depois escrevê-la no âmbito da segunda linha no dez milhares coluna; se ele tem dois dígitos, em seguida, escrever o último dígito para baixo sob a linha no dez milhares colunas, e realizar o primeiro dígito até a centenas de milhares-colunas, escrevê-lo como um expoente para o ainda-não-escrita de dez milhares dígitos sob a linha. No entanto, se a centenas-fila não tem milhares dígitos então não escrever este carry dígitos como um sobrescrito, mas em tamanho normal, na posição do cem-milhares dígitos no âmbito da segunda linha, eo algoritmo de multiplicação é longo .
Se a centenas fileira tem um milhares dígitos, em seguida, adicionar a ele o carry dígitos da linha anterior (se não há carry dígitos, em seguida, pense nisso como um zero) e escrever a soma de um dígito no centena -thousands-coluna sob a segunda linha.
O número abaixo da segunda linha é o produto procurado do par de fatores acima da primeira linha.
Exemplo
Deixe o nosso objectivo ser o de encontrar o produto de 789 e 345. Faça o 345 sob as 789 em três colunas, e desenhar uma linha horizontal sob eles:
| 7 | 8 | 9 |
| 3 | 4 | 5 |
Primeira parte. Comece com os de coluna. O multiplicando é 789 e os de multiplicador é 5. Execute a multiplicação em uma linha sob a linha:
| 7 | 8 | 9 | |
| 3 | 4 | 5 | |
| 3 | 9 4 | 4 4 | 5 |
Em seguida, a dezenas-coluna.O multiplicando é 789 e as dezenas multiplicador é 4. Execute a multiplicação, na dezenas-linha, sob o subproduto anterior na queridos-linha, mas deslocou uma coluna para a esquerda:
| 7 | 8 | 9 | ||
| 3 | 4 | 5 | ||
| 3 | 94 | 44 | 5 | |
| 3 | 13 | 53 | 6 |
Em seguida, a centenas colunas. O multiplicando é mais uma vez 789, ea centenas multiplicador é 3. Execute a multiplicação no centenas carreiras, sob o subproduto anterior na dezenas-linha, mas deslocou uma coluna (mais) para a esquerda. Em seguida, desenhe uma linha horizontal sob a centenas-fila:
| 7 | 8 | 9 | |||
| 3 | 4 | 5 | |||
| 3 | 94 | 44 | 5 | ||
| 3 | 13 | 53 | 6 | ||
| 2 | 32 | 62 | 7 |
Segunda parte.Agora adicione os subprodutos entre as primeira e segunda linhas, mas ignorando quaisquer transições de dígitos sobrescritos localizada entre a primeira e segunda linhas.
| 7 | 8 | 9 | |||
| 3 | 4 | 5 | |||
| 3 | 94 | 44 | 5 | ||
| 3 | 13 | 53 | 6 | ||
| 2 | 32 | 62 | 7 | ||
| 2 | 71 | 22 | 21 | 0 | 5 |
A resposta é