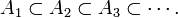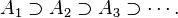Emmy Noether
Fundo para as escolas Wikipédia
Crianças SOS oferecem um download completo desta seleção para as escolas para uso em escolas intranets. Patrocinar crianças ajuda crianças no mundo em desenvolvimento para aprender também.
| Emmy Noether | |
|---|---|
 | |
| Nascido | Amalie Emmy Noether 23 de março de 1882 Erlangen, Bavaria, Alemanha |
| Morreu | 14 de abril de 1935 (idade 53) Bryn Mawr, na Pensilvânia, EUA |
| Nacionalidade | Alemão |
| Campos | Matemática e física |
| Instituições | Universidade de Göttingen Bryn Mawr College |
| Alma mater | Universidade de Erlangen |
| Conselheiro doutoral | Paul Gordan |
| Os estudantes de doutorado | Max Deuring Hans Fitting Grete Hermann Zeng Jiongzhi Jacob Levitzki Otto Schilling Ernst Witt |
| Conhecido por | Abstract álgebra A física teórica |
Emmy Noether (alemão: [Nøːtɐ]; nome oficial Amalie Emmy Noether, 23 de março de 1882 - 14 de abril 1935), foi um influente Alemão matemático conhecido por suas contribuições inovadoras para álgebra abstrata e física teórica. Descrito por Pavel Alexandrov, Albert Einstein , Jean Dieudonné, Hermann Weyl, Norbert Wiener e outros como a mulher mais importante na história da matemática, ela revolucionou as teorias de anéis, campos, e álgebras. Em física, Teorema de Noether explica a conexão fundamental entre simetria e leis de conservação.
Ela nasceu em uma família judia na Cidade bávara de Erlangen; seu pai era matemático Max Noether. Emmy originalmente planejado para ensinar Francês e Inglês, depois de passar os exames necessários, mas em vez disso estudou matemática na Universidade de Erlangen, onde seu pai palestras. Depois de completar sua dissertação em 1907 sob a supervisão de Paul Gordan, trabalhou no Instituto de Matemática de Erlangen sem remuneração por sete anos (na época as mulheres eram, em grande parte excluídas de posições acadêmicas). Em 1915, ela foi convidada por David Hilbert e Felix Klein para se juntar ao departamento de matemática na Universidade de Göttingen, um centro de renome mundial de investigação matemática. A faculdade de filosofia opôs, no entanto, e ela passou quatro anos lecionando sob o nome de Hilbert. Seu habilitação foi aprovado em 1919, permitindo-lhe obter a classificação de Privatdozent.
Noether permaneceu um dos principais membros do Göttingen departamento de matemática até 1933; seus alunos foram chamados às vezes os "meninos de Noether". Em 1924, o matemático holandês BL van der Waerden se juntou a seu círculo e logo se tornou o expositor líder de idéias de Noether: seu trabalho foi a base para o segundo volume de seu influente livro de 1931, Moderne Algebra. Até o momento da sua endereço plenária de 1932 Congresso Internacional de Matemáticos em Zurique , sua perspicácia algébrica foi reconhecido em todo o mundo. No ano seguinte, o governo nazista da Alemanha indeferiu judeus de cargos universitários, e Noether se mudou para os Estados Unidos para ocupar um cargo na Bryn Mawr College, em Pennsylvania. Em 1935, ela se submeteu a cirurgia para uma cisto de ovário e, apesar dos sinais de uma recuperação, morreu quatro dias mais tarde na idade de 53.
Trabalho matemático de Noether foi dividida em três "épocas". No primeiro (1908- 19 ), ela fez contribuições significativas para as teorias de invariantes algébricos e campos de números. Seu trabalho em invariantes diferenciais no cálculo das variações , Teorema de Noether, tem sido chamado de "um dos teoremas matemáticos mais importantes já provadas para orientar o desenvolvimento da física moderna". Na segunda época (1920- 26 ), ela começou a trabalhar que "mudou a face do [resumo] álgebra". Em seu artigo clássico Idealtheorie em Ringbereichen (Teoria de ideais em anel Domains, 1921) Noether desenvolveu a teoria da ideais em anéis comutativos em uma poderosa ferramenta com aplicações abrangentes. Ela fez uso elegante da ascendente condição da cadeia e objetos de satisfazê-la são nomeados Noetheriano em sua honra. Na terceira época (1927- 35 ), ela publicou obras importantes em álgebras não comutativas e números hypercomplex e uniu o teoria da representação de grupos com a teoria da módulos e ideais. Além de suas próprias publicações, Noether foi generoso com suas idéias e é creditado com várias linhas de pesquisa publicados por outros matemáticos, mesmo em áreas muito distantes de seu principal trabalho, tais como topologia algébrica.
Biografia

O pai de Emmy, Max Noether, era descendente de uma família de comerciantes grossistas na Alemanha. Ele havia sido paralisado pela poliomielite na idade de quatorze anos. Ele recuperou a mobilidade, mas permaneceu uma perna afetada. Em grande parte autodidata, ele foi premiado com um doutoramento do Universidade de Heidelberg, em 1868. Depois de ensinar lá por sete anos, ele assumiu uma posição na cidade bávara de Erlangen, onde conheceu e casou-se com Ida Amalia Kaufmann, a filha de um próspero comerciante. Contribuições matemáticas de Max Noether fosse geometria algébrica principalmente, seguindo os passos de Alfred Clebsch. Seus melhores resultados conhecidos são o Brill-Noether teorema e o resíduo, ou AF + BG teorema; vários outros teoremas estão associados com ele, incluindo Teorema de Noether Max.
Emmy Noether nasceu em 23 de março 1882, o primeiro de quatro filhos. Seu primeiro nome foi "Amalie", depois que sua mãe e sua avó paterna, mas ela começou a usar seu nome do meio em uma idade jovem. Como uma menina, ela era muito querido. Ela não se destacam academicamente embora ela era conhecida por ser inteligente e amigável. Emmy foi míope e conversou com um menor lisp durante a infância. Um amigo da família contou uma história anos mais tarde sobre o jovem Emmy resolver rapidamente um quebra-cabeças em uma festa infantil, mostrando perspicácia lógicas nessa idade precoce. Emmy foi ensinado a cozinhar e limpar, assim como a maioria das meninas da época, e ela teve aulas de piano. Ela perseguiu nenhuma dessas atividades com paixão, embora ela adorava dançar.
Ela tinha três irmãos mais novos. O mais velho, Alfred, nasceu em 1883, foi premiado com um doutorado em química de Erlangen, em 1909, mas morreu nove anos depois. Fritz Noether, nascido em 1884, é lembrado por suas realizações acadêmicas: depois de estudar em Munique ele fez uma reputação para si mesmo em matemática aplicada . O mais novo, Gustav Robert, nasceu em 1889. Muito pouco se sabe sobre sua vida; ele sofria de doença crônica e morreu em 1928.
Universidade de Erlangen

Emmy Noether mostrou proficiência no início de Francês e Inglês. Na primavera de 1900 ela fez o exame para professores de línguas e recebeu uma pontuação global de sehr gut (muito bom). Seu desempenho a qualificou para ensinar línguas nas escolas reservados para as meninas, mas ela preferiu continuar seus estudos na Universidade de Erlangen.
Esta foi uma decisão não convencional; dois anos antes, o Senado Académico da universidade declarou que só permitindo coeducação seria "derrubar toda a ordem acadêmica". Um dos dois únicos mulheres estudantes em uma universidade de 986, Noether só foi permitida a aulas de auditoria em vez de participar plenamente, e exigiu a permissão de professores individuais cujas palestras que desejava participar. Apesar dos obstáculos, em 14 de julho de 1903 ela passou no exame de graduação na Realgymnasium em Nuremberg.
Durante o semestre de inverno 1903-1904, ela estudou na Universidade de Göttingen, assistir a palestras dadas pelo astrônomo Karl Schwarzschild e matemáticos Hermann Minkowski, Otto Blumenthal, Felix Klein e David Hilbert . Logo depois disso, restrições à participação das mulheres na universidade que foram revogadas.
Noether devolvido para erlangen. Ela entrou novamente oficialmente a universidade em 24 de Outubro de 1904, e declarou a sua intenção de se concentrar apenas na matemática. Sob a supervisão de Paul Gordan ela escreveu sua dissertação, Über die Bildung des Formensystems der ternären biquadratischen Form (On Sistemas completos de invariantes para formulários Ternary biquadrática, 1907). Embora tenha sido bem recebido, Noether mais tarde descreveu sua tese como "porcaria".
Para os próximos sete anos (1908- 15 ), ela ensinou na Universidade do Instituto de Matemática da Erlangen sem remuneração, por vezes substituindo seu pai quando ele estava doente demais para lecionar. Em 1910 e 1911, ela publicou uma extensão do seu trabalho de tese a partir de três variáveis para n variáveis.

Gordan aposentado na primavera de 1910, mas continuou a ensinar, ocasionalmente, com o seu sucessor, Erhard Schmidt, que saiu pouco depois para uma posição em Breslau. Gordan se aposentou por completo em 1911, com a chegada do sucessor de Schmidt Ernst Fischer, e morreu em dezembro 1912.
Conforme Hermann Weyl, Fischer foi uma influência importante sobre Noether, em particular através da introdução de ela para o trabalho de David Hilbert . A partir de 1913-1916 Noether publicou vários artigos que se estendem e aplicação de métodos de Hilbert para objetos matemáticos tais como campos de funções racionais eo invariantes de grupos finitos. Esta fase marca o início de seu noivado com álgebra abstrata , o campo da matemática para que ela iria fazer contribuições inovadoras.
Noether e Fischer compartilhada diversão animada da matemática e muitas vezes iria discutir palestras muito tempo depois eles foram mais; Noether é conhecido por ter enviado cartões postais de Fischer continuando seu trem de pensamentos matemáticos.
Universidade de Göttingen
Na primavera de 1915, Noether foi convidado a retornar para a Universidade de Göttingen por David Hilbert e Felix Klein. Seu esforço para recrutá-la, no entanto, foi bloqueada pelo filólogos e historiadores entre a faculdade de filosofia: as mulheres, eles insistiram, não deve tornar-se privatdozent. Um membro do corpo docente protestou: "O que vai pensar nossos soldados quando eles retornam para a universidade e achar que eles são obrigados a aprender aos pés de uma mulher?" Hilbert respondeu com indignação, afirmando: "Eu não vejo que o sexo do candidato é um argumento contra sua admissão como privatdozent. Afinal de contas, nós somos uma universidade, não uma casa de banho."

Noether deixou para Göttingen no final de abril; duas semanas depois que sua mãe morreu de repente em Erlangen. Ela já havia recebido atendimento médico para uma condição de olho, mas sua natureza e impacto sobre a sua morte é desconhecida. Mais ou menos ao mesmo tempo, o pai de Noether aposentado e seu irmão se juntou ao Exército alemão para servir na Primeira Guerra Mundial . Ela voltou a Erlangen por várias semanas, principalmente para cuidar de seu pai idoso.
Durante seus primeiros anos de ensino em Göttingen, ela não tem uma posição oficial e não foi paga; sua família pagou por sua casa e comida e apoiou seu trabalho acadêmico. Suas palestras muitas vezes foram anunciados sob o nome de Hilbert, e Noether iria fornecer "assistência".
Logo depois de chegar em Göttingen, no entanto, ela demonstrou suas capacidades, provando o teorema hoje conhecido como Teorema de Noether, que mostra que um lei de conservação está associado com qualquer diferenciável simetria de um sistema físico. Físicos americanos Leon Lederman e M. Christopher T. Monte argumentam em seu livro Symmetry eo Universo bonita que o teorema de Noether é "certamente um dos teoremas matemáticos mais importantes já provadas para orientar o desenvolvimento da física moderna, possivelmente em pé de igualdade com o teorema de Pitágoras ".

Quando a Primeira Guerra Mundial terminou, o Revolução Alemã de 1918-19 trouxe uma mudança significativa nas atitudes sociais, incluindo mais direitos para as mulheres. Em 1919, a Universidade de Göttingen permitido Noether para prosseguir com ela habilitação (elegibilidade para a posse). O exame oral foi realizada no final de maio, e ela entregou com sucesso sua palestra de habilitação em junho.
Três anos mais tarde, ela recebeu uma carta do Ministro prussiano da Ciência, Arte e Educação Pública, na qual ele conferiu-lhe o título de Professor nicht beamteter ausserordentlicher (um professor untenured com direitos administrativos internos limitados e funções). Este foi um professor não remunerado "extraordinária", e não o professor superior "ordinário", que era uma posição de serviço civil. Embora se reconheça a importância de seu trabalho, a posição ainda não forneceu salário. Noether não foi pago por suas palestras, até que foi nomeado para o cargo especial de Lehrbeauftragte für Álgebra um ano depois.
Trabalho seminal em álgebra abstrata
Embora o teorema de Noether teve um profundo efeito sobre a física, entre os matemáticos, ela é mais lembrado por suas contribuições seminais para álgebra abstrata . Como Nathan Jacobson diz em sua introdução ao Collected Papers de Noether,
O desenvolvimento da álgebra abstrata, que é uma das inovações mais marcantes da matemática do século XX, é em grande parte devido a ela - em artigos publicados, em palestras e na influência pessoal sobre seus contemporâneos.
Trabalho inovador de Noether em álgebra começou em 1920. Em colaboração com W. Schmeidler, ela, então, publicou um artigo sobre o teoria dos ideais em que se definidos ideais de esquerda e direita em um anel. No ano seguinte, publicou um artigo chamado marco Idealtheorie em Ringbereichen, analisando ascendente condições da cadeia no que respeita à (matemáticas) ideais. Algebraist observou Irving Kaplansky chamado este trabalho "revolucionário"; a publicação deu origem ao termo " Anel Noetheriano ", e vários outros objetos matemáticos sendo chamado Noetheriano.
Em 1924, um jovem matemático holandês, BL van der Waerden, chegou na Universidade de Göttingen. Ele imediatamente começou a trabalhar com Noether, que forneceu métodos inestimáveis de conceituação abstrata. van der Waerden disse mais tarde que sua originalidade era "absoluta além comparação". Em 1931 ele publicou Moderne Algebra, um texto central no campo; seu segundo volume emprestado pesadamente de trabalho de Noether. Embora Emmy Noether não buscar o reconhecimento, ele incluiu como uma nota na sétima edição "baseado em parte em palestras de E. Artin e E. Noether ". Às vezes ela permitiu que seus colegas e alunos para receber o crédito por suas idéias, ajudando-os a desenvolver suas carreiras em detrimento da sua própria.
visita van der Waerden era parte de uma convergência de matemáticos de todo o mundo para Göttingen, que se tornou um importante centro de pesquisa matemática e física. A partir de 1926-1930 russo topologist Pavel Alexandrov lecionou na universidade, e ele e Noether rapidamente se tornaram bons amigos. Ele começou a se referir a ela como der Noether, usando o artigo alemão masculino como um termo carinhoso para mostrar seu respeito. Ela tentou se organizar para ele para obter uma posição em Göttingen como professor regular, mas só foi capaz de ajudá-lo a garantir uma bolsa de estudos do Fundação Rockefeller. Eles reuniram-se regularmente e gostava de discussões sobre as interseções de álgebra e topologia. Em seu 1935 memorial endereço, Alexandrov nomeado Emmy Noether "o maior matemático mulher de todos os tempos".
Palestras e estudantes
Em Göttingen, Noether supervisionado mais de uma dúzia de estudantes de doutorado; ela foi primeiro Grete Hermann, que defendeu sua dissertação em fevereiro de 1925. Mais tarde, ela falou com reverência de sua "tese-mãe" .. Noether também supervisionou Max Deuring, que se distinguiu como uma graduação e passou a contribuir significativamente para o campo de geometria aritmética; Hans Fitting, lembrado por Montagem do teorema eo Fitting lema; e Zeng Jiongzhi (também traduzido por "Chiungtze C. Tsen", em Inglês), que provou Teorema de Tsen. Ela também trabalhou em estreita colaboração com Wolfgang Krull, que muito avançada álgebra comutativa com sua Hauptidealsatz e sua teoria da dimensão de anéis comutativos.
Além de sua intuição matemática, Noether foi respeitada pela sua consideração pelos outros. Embora às vezes ela agiu brutalmente para com aqueles que não concordavam com ela, ela, no entanto, ganhou uma reputação de utilidade constante e orientação paciente de novos alunos. Sua lealdade para com precisão matemática causado um colega para chamá-la de "um crítico severo", mas ela combinou essa demanda de precisão com uma atitude carinho. Um colega mais tarde descreveu desta maneira: "Completamente unegotistical e livre de vaidade, ela nunca disse nada para si, mas promoveu os trabalhos de seus alunos acima de tudo."
Seu estilo de vida frugal no primeiro foi devido ao pagamento a ser negado pelo seu trabalho; no entanto, mesmo depois de a universidade começou a pagar-lhe um pequeno salário em 1923, ela continuou a viver uma vida simples e modesta. Ela foi pago mais generosamente mais tarde em sua vida, mas metade salvo de seu salário de legar a seu sobrinho, Gottfried E. Noether.
Principalmente despreocupado com aparência e os costumes, ela se concentrou em seus estudos para a exclusão de romance e moda. A algebraist distinto Olga Taussky-Todd descreveu um almoço, durante o qual Noether, totalmente absorto em uma discussão de matemática ", gesticulava loucamente", como ela comeu e "derramou sua comida constantemente e limpou-off de seu vestido, completamente imperturbável". Estudantes preocupados com a aparência se encolheu quando ela pegou o lenço de sua blusa e ignorou a crescente desordem de seu cabelo durante uma palestra. Dois estudantes do sexo feminino, uma vez aproximou-se dela durante uma pausa em uma aula de duas horas para expressar sua preocupação, mas eles não foram capazes de romper a discussão matemática energética ela estava tendo com outros estudantes.
De acordo com o obituário de Emmy Noether van der Waerden, ela não seguiu um plano de aula para suas palestras, o que frustrou alguns alunos. Em vez disso, ela usou suas palestras como um tempo de discussão espontânea com seus alunos, para pensar e esclarecer importantes problemas de ponta em matemática. Alguns de seus resultados mais importantes foram desenvolvidos nessas palestras, e as notas de aula de seus alunos formaram a base para vários livros importantes, como as de van der Waerden e Deuring.
Vários de seus colegas assistiram suas palestras, e ela permitiu que alguns de suas idéias, como a cruzado produto (verschränktes Produkt em alemão) de álgebras associativas, a ser publicado por outros. Noether foi registrado como tendo dado pelo menos cinco cursos semestrais em Göttingen:
- Inverno 1924/25: Gruppentheorie hyperkomplexe und Zahlen (teoria de grupo e hypercomplex Numbers)
- Inverno 1927/28: Hyperkomplexe Grossen und Darstellungstheorie (hypercomplex Quantidades e Teoria das Representações)
- Verão 1928: Nichtkommutative Álgebra (Álgebra não comutativa)
- Verão 1929: Nichtkommutative Arithmetik (não comutativa Aritmética)
- Inverno 1929/30: Algebra der Grossen hyperkomplexen (Álgebra de hypercomplex Quantidades).
Estes cursos geralmente precedidos principais publicações nessas áreas.
Noether falou rapidamente, refletindo a velocidade de seus pensamentos, muitos disseram-e exigiu grande concentração de seus alunos. Os alunos que não gostavam de seu estilo de muitas vezes se sentia alienado. Alguns alunos sentiam que ela confiou demasiado em discussões espontâneas. Seus alunos mais dedicados, no entanto, apreciava o entusiasmo com que ela se aproximou matemática, especialmente desde que suas palestras muitas vezes construídos em trabalhos anteriores que tinham feito juntos.
Ela desenvolveu um círculo íntimo de colegas e alunos que pensavam de forma semelhante e tendiam a excluir aqueles que não fizeram. "outsiders" que ocasionalmente visitadas palestras de Noether geralmente gasto apenas 30 minutos na sala antes de sair em frustração ou confusão. Um aluno regular disse de um desses casos: "O inimigo foi derrotado, ele limpou para fora."
Noether mostrou uma devoção ao seu tema e seus alunos que se estendiam para além do dia acadêmico. Uma vez, quando o edifício foi fechado por um feriado estadual, ela reuniu a classe nos degraus do lado de fora, levou-os através das madeiras, e lecionou em uma casa de café local. Mais tarde, depois de ter sido demitido pelo Terceiro Reich , ela convidou os alunos em sua casa para discutir seus planos futuros e conceitos matemáticos.
Moscou

No inverno de 1928-29 Noether aceitou um convite para Moscow State University, onde ela continuou a trabalhar com PS Alexandrov. Além de prosseguir com a sua pesquisa, ela dava aulas na álgebra abstrata e geometria algébrica. Ela trabalhou com os topologists, Lev Pontryagin e Nikolai Chebotaryov, que mais tarde elogiou suas contribuições para o desenvolvimento da teoria de Galois .
Embora a política não foi fundamental para sua vida, Noether teve um grande interesse em questões políticas e, segundo a Alexandrov, mostrou um apoio considerável para a Revolução Russa (1917) . Ela estava especialmente feliz por ver soviéticos avanços nos campos da ciência e da matemática, que ela considerava indicativo de novas oportunidades possibilitadas pela Projeto bolchevique. Esta atitude lhe causou problemas na Alemanha, culminando em sua expulsão de um pensão edifício hospedagem, após líderes estudantis queixou-se de viver com "uma judia marxista-inclinando-se".

Noether planejado para voltar a Moscou, um esforço pelo qual recebeu o apoio de Alexandrov. Depois que ela deixou a Alemanha em 1933, ele tentou ajudá-la a ganhar uma cadeira na Universidade Estatal de Moscovo através do Ministério da Educação Soviética. Apesar desse esforço não foi bem sucedida, eles corresponderam com freqüência durante a década de 1930, e em 1935 ela fez planos para um retorno à União Soviética. Enquanto isso, seu irmão, Fritz aceitou um cargo no Instituto de Pesquisa de Matemática e Mecânica em Tomsk, na Sibéria Distrito Federal da Rússia, depois de perder seu emprego na Alemanha.
Reconhecimento
Em 1932 Emmy Noether e Emil Artin recebeu o Ackermann-Teubner Memorial Award por suas contribuições para a matemática. O prêmio realizada uma recompensa monetária de 500 Reichsmarks e era visto como um reconhecimento oficial de longo atraso de seu trabalho considerável no campo. No entanto, seus colegas expressaram frustração com o fato de que ela não foi eleito para o Göttingen Gesellschaft der Wissenschaften (Academia das Ciências) e nunca foi promovido para o cargo de Professor Ordentlicher (professor titular).

Os colegas de Noether comemorou seu quinquagésimo aniversário, em 1932, no estilo dos matemáticos típicos. Helmut Hasse dedicado um artigo com ela no Mathematische Annalen, em que ele confirmou sua suspeita de que alguns aspectos da álgebra não-comutativa são mais simples do que os de álgebra comutativa, provando a não-comutativa lei da reciprocidade. Isso agradou muito. Ele também enviou-lhe um enigma matemático, o "mμν-enigma de sílabas", que ela resolvidos imediatamente; o enigma foi perdida.
Em novembro do mesmo ano, Noether fez um discurso plenário (Vortrag großer) em "sistemas Hyper-complexas nas suas relações com comutativa álgebra e teoria dos números" no Congresso Internacional de Matemáticos, em Zurique . O congresso contou com a presença de 800 pessoas, incluindo colegas de Noether Hermann Weyl, Edmund Landau, e Wolfgang Krull. Havia 420 participantes oficiais e vinte e um endereços plenárias apresentadas. Aparentemente, a posição de destaque falar de Noether era um reconhecimento da importância de suas contribuições para a matemática. O congresso 1932 às vezes é descrito como o ponto alto da sua carreira.
Expulsão de Göttingen
Quando Adolf Hitler tornou-se o Chanceler alemão em janeiro de 1933, Nazi atividade em todo o país aumentou dramaticamente. Na Universidade de Göttingen a Associação de Estudantes alemão liderou o ataque contra o "espírito não-alemão" atribuído a judeus e foi ajudado por um privatdozent chamado Werner Weber, um ex-aluno de Emmy Noether. Atitudes anti-semitas criaram um clima hostil para professores judeus. Um jovem manifestante teria exigido: "Os estudantes arianos querem matemática arianos e matemática não judeu".
Uma das primeiras ações do governo de Hitler era o Lei para a Restauração do Serviço Civil Profissional que removeu os judeus e os funcionários públicos politicamente suspeitos (incluindo professores universitários) de seus empregos a menos que eles tinham "demonstrou sua lealdade para a Alemanha", servindo na Primeira Guerra Mundial Em abril de 1933 Noether recebeu um aviso de o Ministério Prussiano de Ciências, Artes e Educação Pública, que dizia: "Com base no n.º 3 do Código Civil de 7 de Abril de 1933, tenho a honra de retirar-lhe o direito de ensinar na Universidade de Göttingen." Vários dos colegas de Noether, inclusive Max Born e Richard Courant, também tiveram suas posições revogada. Noether aceitou a decisão com calma, fornecendo suporte para os outros durante este tempo difícil. Hermann Weyl escreveu mais tarde que "Emmy Noether-sua coragem, sua franqueza, sua despreocupação sobre seu próprio destino, seu espírito conciliador-se no meio de todo o ódio e maldade, desespero e tristeza que nos rodeia, um consolo moral." Normalmente, Noether permaneceu focada em matemática, reunindo estudantes em seu apartamento para discutir teoria do campo de classe. Quando um de seus alunos apareceu no uniforme da organização paramilitar nazista Sturmabteilung (SA), ela não mostrou nenhum sinal de agitação e, alegadamente, até riu sobre isso mais tarde.
Bryn Mawr

Como dezenas de professores recém-desempregados começou a procurar por posições fora da Alemanha, seus colegas nos Estados Unidos procuraram para oferecer oportunidades de assistência e de emprego para eles. Albert Einstein e Hermann Weyl foram nomeados pelo Instituto de Estudos Avançados em Princeton, enquanto outros trabalharam para encontrar um patrocinador necessária para legal imigração. Noether foi contatado por representantes de duas instituições de ensino, Bryn Mawr College, nos Estados Unidos e Somerville College da Universidade de Oxford , na Inglaterra. Após uma série de negociações com o Rockefeller Foundation, uma subvenção para Bryn Mawr foi aprovado para Noether e ela tomou uma posição lá, começando no final de 1933.
No Bryn Mawr, Noether conheceu e fez amizade Anna Wheeler, que tinha estudado em Göttingen, pouco antes de Noether chegou lá. Outra fonte de apoio na faculdade era o presidente Bryn Mawr, Marion Edwards Park, que entusiasticamente convidou matemáticos na área de "ver Dr. Noether em ação!" Noether e uma pequena equipe de estudantes trabalharam rapidamente através de van der Waerden 1930 Moderne livro Álgebra I e partes da Theorie der algebraischen de Erich Hecke Zahlen (Teoria de números algébricos, 1908).
Em 1934, Noether começou a lecionar no Instituto de Estudos Avançados de Princeton, a convite da Abraham Flexner e Oswald Veblen. Ela também trabalhou com e supervisionados Abraão e Albert Harry Vandiver. No entanto, ela comentou sobre a Universidade de Princeton que ela não era bem-vindo na "universidade dos homens, onde nada fêmea é admitido".
Seu tempo nos Estados Unidos foi agradável, rodeado como estava por colegas de apoio e absorta em seus assuntos favoritos. No verão de 1934 ela retornou brevemente para a Alemanha para ver Emil Artin e seu irmão Fritz antes de partir para Tomsk. Embora muitos de seus ex-colegas tinham sido forçados para fora das universidades, ela foi capaz de usar a biblioteca como um "estudioso estrangeiro".
Morte

Em abril 1935 os médicos descobriram um tumor em Noether de pélvis. Preocupado com complicações da cirurgia, que ordenou dois dias de repouso na cama primeiro. Durante a operação, eles descobriram uma quisto do ovário "do tamanho de um grande melão ". Dois tumores menores em sua útero parecia ser benigna e não foram removidas, para evitar o prolongamento da cirurgia. Durante três dias, ela apareceu para convalescer normalmente, e ela se recuperou rapidamente de uma colapso circulatório no quarto. Em 14 de abril, ela caiu inconsciente, sua temperatura subiu para 109 ° F (42,8 ° C), e ela morreu. "[I] t não é fácil dizer o que havia ocorrido em Dr. Noether", um dos médicos escreveu. "É possível que houve alguma forma de infecção incomum e virulenta, que atingiu a base do cérebro onde os centros de calor devem ser localizados."
Poucos dias depois da morte de Noether seus amigos e associados no Bryn Mawr realizou um pequeno memorial serviço na casa do Colégio Presidente Park. Hermann Weyl e Richard Brauer viajou de Princeton e falou com Wheeler e Taussky sobre o seu colega de partido. Nos meses que se seguiram, homenagens escritas começaram a aparecer ao redor do globo: Albert Einstein juntou van der Waerden, Weyl, e Pavel Alexandrov em pagar seus respeitos. Seu corpo foi cremado e as cinzas enterradas sob a passarela em torno dos claustros da M. Carey Thomas Biblioteca em Bryn Mawr.
As contribuições para a matemática ea física
Em primeiro lugar Noether é lembrado por matemáticos como um algebraist e para seu trabalho na topologia . Os físicos apreciá-la melhor para ela famoso teorema devido às suas consequências de longo alcance para física teórica e sistemas dinâmicos. Ela mostrou uma propensão aguda para o pensamento abstrato, o que lhe permitiu abordar os problemas de matemática de maneiras novas e originais. Sua amiga e colega Hermann Weyl descreveu sua saída acadêmica em três épocas:
Produção científica de Emmy Noether caiu em três épocas claramente distintos:(1) o período de dependência relativa, 1907-1919;
(3) o estudo da álgebra não-comutativa, suas representações de transformações lineares, ea sua aplicação ao estudo de campos de números comutativos e seus aritmética.
(2) as investigações agrupados em torno da teoria geral dos ideais 1920-1926;-Weyl 1935
Na primeira época (1907-1919), Noether tratou principalmente com diferenciais e algébricas invariantes, começando com sua dissertação sob Paul Gordan. Seus horizontes matemáticas ampliou, e seu trabalho se tornou mais geral e abstracto, como ela conheceu o trabalho de David Hilbert , através de interações estreitas com um sucessor para Gordan, Ernst Sigismund Fischer. Após se mudar para Göttingen em 1915, ela produziu sua obra seminal para a física, os dois Teoremas de Noether.
Na segunda época (1920-1926), Noether dedicou-se a desenvolver a teoria da anéis matemáticos.
No terceiro epoch (1927-1935), Noether focado em álgebra não-comutativa, transformações lineares, e campos de número comutativo.
Contexto histórico
No século de 1832 a morte de Noether em 1935, no campo da matemática, especificamente álgebra -underwent uma profunda revolução, cujas reverberações ainda estão sendo sentidos. Os matemáticos de séculos anteriores havia trabalhado em métodos práticos para resolver tipos específicos de equações, por exemplo, cúbico, quártico, e equações de quinto grau, bem como sobre o problema relacionado de construção polígonos regulares usando régua e compasso . Começando com Carl Friedrich Gauss 1.832 prova 's que números primos tais como cinco pode ser consignado em Inteiros de Gauss, Introdução de Évariste de Galois grupos de permutação em 1832 (embora, por causa de sua morte, seus trabalhos foram publicados apenas em 1846 por Liouville), Descoberta de William Rowan Hamilton quaternions em 1843, e Definição mais moderna de Arthur Cayley de grupos em 1854, a pesquisa voltou-se para a determinação das propriedades de sistemas cada vez mais abstratas definidos pelas regras cada vez mais universais. Mais importantes contribuições para a matemática de Noether fosse para o desenvolvimento desse novo campo, álgebra abstrata .
Abstract álgebra e begriffliche Mathematik (matemática conceptual)
Dois dos mais objetos básicos em álgebra abstrata são grupos e anéis.
Um grupo é constituído por um conjunto de elementos e uma única operação, que combina um primeiro e um segundo elemento e retorna um terceiro. A operação deve satisfazer certas restrições por ele para determinar um grupo: Ele deve ser fechada (quando aplicado a qualquer par de elementos do conjunto associado, o elemento gerado também deve ser um membro desse conjunto), deve ser associativa , não deve ser um elemento de identidade (de um elemento que, quando combinado com outro elemento utilizando a operação, resulta em o elemento original, tais como adicionando um número de zero a ou multiplicando-o por um), e por cada elemento deve ser um elemento inverso.
Um anel de igual modo, tem um conjunto de elementos, mas agora tem duas operações. A primeira operação deve fazer o conjunto de um grupo, e a segunda operação é associativa e distributivos com respeito à primeira operação. Ele pode ou não ser comutativa ; isto significa que o resultado da aplicação da operação de um primeiro e um segundo elemento é a mesma que para a segunda e primeira a ordem dos elementos não tem importância. Se cada elemento diferente de zero tem um inverso multiplicativo (um elemento tal que x = ax xa = 1), o anel é chamado um anel de divisão. A campo é definido como um anel de divisão conmutativo.
Os grupos são frequentemente estudadas através de as representações do grupo . Na sua forma mais geral, trata-se de uma escolha de grupo, um conjunto, e uma ação do grupo sobre o conjunto, ou seja, uma operação que leva um elemento do grupo e um elemento do conjunto e retorna um elemento de o conjunto. Na maioria das vezes, o conjunto é um espaço vetorial , eo grupo representa simetrias do espaço vetorial. Por exemplo, há um grupo que representa as rotações rígidas de espaço. Este é um tipo de simetria de espaço, porque o espaço em si não muda quando ele é rodado, embora as posições dos objectos no que fazer. Noether usado esses tipos de simetrias em seu trabalho sobre invariantes em física.
Uma forma poderosa de estudar anéis é através de seus módulos . Um módulo é constituído por uma escolha de anel, um outro conjunto, geralmente distinto do conjunto do anel subjacente e designado por conjunto subjacente do módulo, uma operação em pares de elementos do conjunto do módulo subjacente, e uma operação que demora um elemento do anel e um elemento do módulo e retorna um elemento do módulo. O subjacente conjunto de módulo e seu funcionamento devem formar um grupo. Um módulo é uma versão anel de teoria de uma representação grupo: Ignorando a segunda operação anel ea operação em pares de elementos do módulo determina uma representação grupo. A utilidade real dos módulos é que os tipos de módulos existentes e as suas interacções, revelam a estrutura do anel de maneira que não são visíveis a partir do próprio anel. Um caso especial importante disso é uma álgebra . (A palavra álgebra significa tanto um objecto dentro de matemática, bem como um objecto estudado no assunto da álgebra.) Uma álgebra consiste de uma escolha de dois anéis e uma operação que tem um elemento de cada anel e retorna um elemento do segundo anel . Esta operação faz com que o segundo anel em um módulo em relação ao primeiro. Muitas vezes o primeiro anel é um campo.
Palavras como "elemento" e "combinação de operação" são muito gerais, e pode ser aplicado a muitas situações do mundo real e abstratas. Qualquer conjunto de coisas que obedece a todas as regras para um (ou dois) operação (s) é, por definição, um grupo (ou anel), e obedece a todos os teoremas sobre grupos (ou anéis). Os números inteiros, e as operações de adição e multiplicação, são apenas um exemplo. Por exemplo, os elementos podem ser palavras de dados de computador, em que a primeira operação de combinação é exclusiva ou e o segundo é conjunção lógica. Teoremas de álgebra abstrata são poderosos, porque eles são em geral; eles governam muitos sistemas. Pode-se imaginar que pouco poderia ser concluído sobre objetos definidos com tão poucas propriedades, mas precisamente aí estava o presente de Noether: para descobrir o máximo que pôde ser concluído a partir de um determinado conjunto de propriedades, ou, inversamente, para identificar o conjunto mínimo, o essencial propriedades responsáveis por uma observação especial . Diferentemente da maioria dos matemáticos, ela não fez abstrações por generalizar a partir de exemplos conhecidos; em vez disso, ela trabalhou diretamente com as abstrações. Como van der Waerden lembrou em seu obituário dela,
A máxima de que Emmy Noether era guiado por todo o seu trabalho pode ser formulado da seguinte forma: "Todas as relações entre números, funções e operações tornam-se transparentes, de aplicação geral, e plenamente produtivo só depois de terem sido isoladas de seus objetos particulares e foi formulada como conceitos universalmente válidas.
Este é o begriffliche Mathematik (matemática puramente conceitual) que era característico de Noether. Este estilo de matemática foi adotado por outros matemáticos e, após sua morte, florescido em novas formas, tais como teoria da categoria.
Inteiros como um exemplo de um anel
Os números inteiros formam um anel comutativo cujos elementos são os números inteiros, e as operações são combinando adição e multiplicação. Qualquer par de números inteiros podem ser adicionados ou multiplicados , sempre resultante noutro número inteiro, e a primeira operação, além disso, é conmutativo , isto é, para qualquer elementos a e b no anel, um + b = b + um . A segunda operação, a multiplicação, também é conmutativo, mas que não tem que ser verdadeiro para outros anéis, o que significa que uma combinados com b pode ser diferente de b combinado com um . Exemplos de anéis comutatvos incluem matrizes e quaternions. os inteiros não formam um anel de divisão, porque a segunda operação não pode ser sempre invertido; não há nenhum número inteiro um tal modo que 3 × um = 1.
Os números inteiros têm propriedades adicionais que não generalizar para todos os anéis comutativos. Um exemplo importante é o teorema fundamental da aritmética , que diz que todo inteiro positivo pode ser tomada exclusivamente em números primos . Fatorações únicos nem sempre existem em outros anéis, mas Noether encontrado um teorema fatoração única, agora chamado de teorema de Noether-Lasker , para os ideais de muitos anéis. Muito do trabalho de Noether consistia em determinar quais propriedades não segure por todos os anéis, na concepção de novos análogos dos antigos teoremas inteiros, e para determinar o conjunto mínimo de premissas necessárias para produzir certas propriedades de anéis.
Primeira época (1908-1919)
Teoria algébrica invariante

Muito do trabalho de Noether na primeira época de sua carreira foi associada com a teoria dos invariantes, principalmente teoria algébrica invariante. Teoria dos invariantes está preocupada com expressões que permanecem constantes (invariantes) sob um grupo de transformações. Como um exemplo, todos os dias, se um critério rígida é rodado, as coordenadas ( x , y , z ) de suas extremidades mudar, mas o seu comprimento L dado pela fórmula G 2 = Δ x 2 Δ + y 2 + Δ z 2 permanece a mesma. Teoria dos invariantes era uma área ativa de pesquisa no final do século XIX, motivados em parte por Felix Klein programa de Erlangen, segundo a qual os diferentes tipos de geometria devem ser caracterizados por suas invariantes sob transformações, por exemplo, o -cross ratio de geometria projetiva. O arquetípica exemplo de uma invariante é a discriminante B 2 - 4 AC de uma forma binária quadrática Ax 2 + Bxy + Cy 2 . Isso é chamado de uma invariante porque é inalterada por substituições lineares x → ax + por , y → cx + dy com determinante ad - bc = 1. Estas substituições formar o grupo especial linear SL 2 . (Não há invariantes sob o grupo linear geral de todas as transformações lineares invertíveis porque essas transformações podem ser multiplicação por um fator de escala. Para remediar esta situação, a teoria invariante clássica também considerou invariantes relativos , que eram formas invariante até um fator de escala.) One pode pedir todos os polinômios em A , B , e C que são alterados pela ação do SL 2 ; estes são chamados de invariantes de formas quadráticas binárias, e acabam por ser os polinômios no discriminante. Em termos mais gerais, pode-se pedir as invariantes de polinômios homogêneos A 0 x r y 0 + ... + A r x 0 y r de grau mais elevado, que serão determinados polinômios nos coeficientes A 0 , ..., A r e, mais geralmente ainda, pode- a pergunta similar para polinômios homogêneos em mais de duas variáveis.
Um dos principais objetivos da teoria dos invariantes era resolver o "problema base finita". A soma ou produto de quaisquer dois invariantes é invariante, e o problema de base finita perguntado se era possível obter todos os invariantes, iniciando com uma lista finita de invariantes, chamados geradores , e, em seguida, adicionando ou multiplicando os geradores juntos. Por exemplo, o discriminante dá uma base finita (com um elemento) para os invariantes de formas quadráticas binárias. Conselheiro de Noether, Paul Gordan, era conhecido como o "rei da teoria dos invariantes", e sua principal contribuição para a matemática era a sua solução 1870 do problema base finita para invariantes de polinômios homogêneos em duas variáveis. Ele provou isso dando um método construtivo para encontrar todos os invariantes e seus geradores, mas não foi capaz de levar a cabo esta abordagem construtiva para invariantes em três ou mais variáveis. Em 1890, David Hilbert mostrou uma declaração semelhante para as invariantes de polinômios homogêneos em qualquer número de variáveis. Além disso, o método de trabalho, não apenas para o grupo linear especial, mas também para alguns dos seus subgrupos, tais como o grupo ortogonal especial. Sua primeira prova causou alguma controvérsia, porque não dar um método para a construção dos geradores, embora em trabalho mais tarde, ele fez o seu método construtivo. Para sua tese, Noether prorrogado prova computacional de Gordan para polinômios homogêneos em três variáveis. Abordagem construtiva de Noether, foi possível estudar as relações entre as invariantes. Mais tarde, depois que ela se transformou em métodos mais abstratos, Noether chamado sua tese de Névoa (porcaria) e Formelngestrüpp (a selva de equações).
Teoria de Galois
Teoria de Galois diz respeito transformações de campos de números que permutar as raízes de uma equação. Considere uma equação polinomial de uma variável x de grau n , em que os coeficientes são retirados de algum campo de terra, que podem ser, por exemplo, o campo de números reais , números racionais , ou os inteiros módulo 7. Não podem ou não ser as escolhas de x , o que torna este polinomial avaliar a zero. Tais escolhas, se existirem, são chamados raízes. Se o polinómio é x 2 + 1 e o campo é os números reais, em seguida, o polinómio não tem raízes, porque qualquer escolha de x faz com que o polinómio maior do que ou igual a um. Se o campo é alargado, no entanto, em seguida, o polinomial pode ganhar raízes, e se ele se estende o suficiente, então ele tem sempre um número de raízes igual ao seu grau. Continuando o exemplo anterior, se o campo é ampliada para os números complexos, então os ganhos polinomiais duas raízes, i e - i , onde i é a unidade imaginária , isto é, i 2 = -1 . Mais geralmente, o campo de extensão no qual uma polinomial podem ser tidos em conta as suas raízes é conhecido como o corpo de decomposição do polinómio.
O Grupo de Galois de um polinômio é o conjunto de todas as formas de transformar o corpo de decomposição, preservando ao mesmo tempo o campo de terra e as raízes do polinômio. (Em linguagem matemática, estas transformações são chamados automorphisms.) O grupo de Galois de x 2 + 1 é composto por dois elementos: A transformação de identidade, o qual envia a cada número complexo a si mesma, e complexo de conjugação, que envia i a - i . Desde que o grupo de Galois não muda o campo de terra, que deixa os coeficientes do polinómio inalterada, por isso, deve deixar o conjunto de todas as raízes inalteradas. Cada raiz pode mudar para outra raiz, no entanto, para transformação determina uma permutação dos n raízes entre si. O significado do grupo de Galois deriva do teorema fundamental da teoria de Galois, o que prova que os campos que se situam entre o domínio do solo e o corpo de decomposição são em correspondência de um-para-um com os subgrupos do grupo de Galois.
Em 1918, Noether publicou um artigo seminal sobre o problema inverso Galois. Em vez de determinar o grupo de Galois de transformações de um dado campo e a sua extensão, Noether perguntado se, dado um campo e um grupo, que é sempre possível encontrar uma extensão do campo que tem o grupo dado como o seu grupo de Galois. Ela reduzida para este " problema de Noether ", que interroga se o campo fixo de um subgrupo G do grupo permutação S n que actua sobre o campo K ( x 1 , ..., x n ) é sempre um puro transcendental extensão do domínio k . (Ela mencionou pela primeira vez este problema em um artigo de 1913, onde ela atribuiu o problema a seu colega Fischer.) Ela mostrou isso era verdade para n = 2 , 3 ou 4. Em 1969, RG Swan encontrado um contra-exemplo para o problema de Noether , com n = 47 e L um grupo cíclico de ordem 47 (embora este grupo pode ser realizado como um grupo de Galois sobre os racionais em outras formas). O inverso problema Galois permanece sem solução.
Física
Noether foi trazido para Göttingen em 1915 por David Hilbert e Felix Klein, que queria a sua experiência na teoria invariante para ajudá-los a compreender a relatividade geral , uma teoria geométrica da gravitação desenvolvido principalmente por Albert Einstein . Hilbert tinha observado que a conservação da energia parecia ser violada na relatividade geral, devido ao fato de que a energia gravitacional poderia gravitar em si. Noether desde que a resolução deste paradoxo, e uma ferramenta fundamental da moderna física teórica, com primeiro teorema de Noether, que ela provou em 1915, mas não publicou até 1918. Ela resolveu o problema não só para a relatividade geral, mas determinou as quantidades conservadas para cada sistema de leis físicas que possui alguma simetria contínua.
Ao receber seu trabalho, Einstein escreveu a Hilbert:. "Ontem recebi de Miss Noether um documento muito interessante sobre invariantes Estou impressionado que tais coisas podem ser entendidas de uma forma tão geral A velha guarda em Göttingen deve tomar algumas lições. senhorita Noether! Ela parece saber as coisas dela. "
Para ilustração, se um sistema físico se comporta da mesma, independentemente da forma como está orientada no espaço, as leis físicas que o regem são simetria de rotação; desta simetria, o teorema de Noether mostra o momento angular do sistema tem de ser conservada. O sistema físico em si não precisa ser simétrica; um asteróide irregular caindo no espaço conserva momento angular apesar de sua assimetria. Em vez disso, a simetria das leis físicas que regem o sistema é responsável pela lei de conservação. Como outro exemplo, se um experimento físico tem o mesmo resultado em qualquer lugar e em qualquer momento, em seguida, suas leis são simétricas sob traduções contínuas no espaço e no tempo; pelo teorema de Noether, essas simetrias conta das leis de conservação de momento linear e energia dentro deste sistema, respectivamente.
Teorema de Noether se tornou uma ferramenta fundamental da moderna física teórica, tanto por causa da percepção que dá para leis de conservação, e também, como uma ferramenta de cálculo prático. Seu teorema permite aos pesquisadores determinar as quantidades conservadas das simetrias observados de um sistema físico. Por outro lado, facilita a descrição de um sistema físico baseado em classes de leis físicas hipotéticos. Para ilustração, suponha que um novo fenômeno físico é descoberto. Teorema de Noether fornece um teste para modelos teóricos do fenómeno: se a teoria tem uma simetria contínua, em seguida, o teorema de Noether garante que a teoria tem uma quantidade conservada, e para que a teoria seja correcta, esta conservação deve ser observável nas experiências.
Segunda época (1920-1926)
Embora os resultados da primeira época de Noether era impressionante e útil, sua fama como um matemático repousa mais sobre o trabalho inovador que ela fez em suas segunda e terceira épocas, como observado por Hermann Weyl e BL van der Waerden em seus obituários dela.
Nessas épocas, ela não se limitou a aplicar ideias e métodos de matemáticos anteriores; em vez disso, ela foi a elaboração de novos sistemas de definições matemáticas que seriam utilizados por matemáticos futuras. Em particular, ela desenvolveu uma teoria completamente nova de ideais em anéis, generalizando trabalho anterior de Richard Dedekind. Ela também é conhecida por desenvolver ascendente condições da cadeia, uma condição finitude simples que produziu resultados poderosos em suas mãos. Essas condições e da teoria dos ideais habilitado Noether generalizar muitos resultados mais velhos e para tratar velhos problemas sob uma nova perspectiva, como a teoria de eliminação e as variedades algébricas que tinham sido estudados por seu pai.
Subindo e descendo as condições da cadeia
Nesta época, Noether se tornou famoso por seu uso hábil de ascendente (Teilerkettensatz) ou descendente (Vielfachenkettensatz) as condições da cadeia. Uma seqüência de não vaziossubconjuntos A 1,A 2,A 3, etc. de umconjunto Sgeralmente é dito serascendente, se cada um é um subconjunto da próxima
Por outro lado, uma sequência de subconjuntos deSé chamadadescendentese cada subconjunto contém o seguinte:
Uma corrente constante, torna-se depois de um número finito de passos , se houver um n de tal modo que 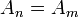 para todos m ≥ n . Um conjunto de subconjuntos de um conjunto dado satisfaz a condição da cadeia ascendente, se qualquer sequência ascendente torna-se constante após um número finito de passos. Satisfaz a condição da cadeia descendente se qualquer sequência descendente se torna constante após um número finito de passos.
para todos m ≥ n . Um conjunto de subconjuntos de um conjunto dado satisfaz a condição da cadeia ascendente, se qualquer sequência ascendente torna-se constante após um número finito de passos. Satisfaz a condição da cadeia descendente se qualquer sequência descendente se torna constante após um número finito de passos.
Condições ascendentes e descendente da cadeia são gerais, o que significa que elas podem ser aplicadas a muitos tipos de objectos matemáticos e, na superfície, que pode não parecer muito poderoso. Noether mostrou como explorar tais condições, no entanto, a vantagem máxima: por exemplo, como usá-los para mostrar que cada conjunto de sub-objetos tem uma máxima / mínima ou elemento que um objeto complexo pode ser gerado por um número menor de elementos . Estas conclusões muitas vezes são passos cruciais em uma prova.
Muitos tipos de objetos em álgebra abstrata pode satisfazer as condições da cadeia, e, geralmente, se satisfizerem uma condição da cadeia ascendente, eles são chamados Noetheriano em sua honra. por definição, um anel Noetheriano satisfaz uma condição da cadeia crescente das suas esquerda e direita ideais, enquanto um grupo Noetheriano é definido como um grupo em que cada cadeia estritamente ascendente de subgrupos é finito. A Noetheriano módulo é um módulo no qual cada cadeia estritamente ascendente de submódulos interrompe após um número finito. A Noetheriano espaço é um espaço topológico no qual cada cadeia estritamente crescente de subespaços abertas quebra após um número finito de termos; esta definição é feita de modo que o espectro de um anel Noetheriano é um espaço topológico Noetheriano.
A condição da cadeia muitas vezes é "herdado" por sub-objetos. Por exemplo, todos os subespaços de um espaço Noetheriano, são Noetheriano si; todos os subgrupos e grupos quociente de um grupo Noetheriano são do mesmo modo, Noetheriano; e, mutatis mutandis , o mesmo vale para submódulos e módulos de quociente de um módulo Noetheriano. Todos os anéis quociente de um anel Noetheriano são Noetheriano, mas isso não significa necessariamente manter por seus subanéis. A condição da cadeia também pode ser herdado por combinações ou extensões de um objeto Noetheriano. Por exemplo, somas finitas diretos de anéis noetherianos são Noetheriano, como é o anel de formal de séries de potência ao longo de um anel Noetheriano.
Outra aplicação de tais condições cadeia está em Noetheriano indução, também conhecido como indução-que bem fundamentada é uma generalização de indução matemática. Ele frequentemente é usado para reduzir declarações gerais sobre coleções de objetos para declarações sobre objetos específicos em que a coleta. Suponha que S é um conjunto parcialmente ordenado. Uma maneira de provar uma declaração sobre os objetos de S é de supor a existência de um contra-exemplo e deduzir uma contradição, provando assim a contrapositiva da declaração original. A premissa básica da indução Noetheriano é que cada subconjunto de vazio não- S contém um elemento mínima. Em particular, o conjunto de todos os contra-elemento contém um mínimo, o contra-mínima . A fim de provar a afirmação original, portanto, é suficiente para provar algo aparentemente muito mais fraca: Para qualquer contra-exemplo, há um contra menores.
Comutativos anéis, ideais e módulos
Papel de Noether, Idealtheorie em Ringbereichen ( Teoria de ideais em anel Domínios , 1921), é o fundamento da teoria geral comutativa anel, e dá uma das primeiras definições gerais de um anel comutativo . Antes de seu papel, a maioria dos resultados em álgebra comutativa eram restritas aos exemplos especiais de anéis comutativos, tais como anéis de polinômios sobre corpos ou anéis de inteiros algébricos. Noether provou que em um anel que satisfaça a condição da cadeia ascendente sobre os ideais, cada ideal é finitamente gerado. Em 1943, o matemático francês Claude Chevalley cunhou o termo, anel Noetheriano , para descrever esta propriedade. Um importante resultado em 1921 papel de Noether é o teorema de Noether-Lasker , que se estende teorema de Lasker na decomposição primária de ideais de anéis de polinômios para todos os anéis noetherianos. O teorema Lasker-Noether pode ser visto como uma generalização do teorema fundamental da aritmética que afirma que qualquer número inteiro positivo pode ser expressa como um produto de números primos , e que esta decomposição é único.
De Noether trabalho Abstrakter Aufbau der Idealtheorie em algebraischen Zahl- und Funktionenkörpern ( Estrutura abstrata da Teoria dos ideais em Algébrica número ea função Campos , 1927) caracterizou os anéis em que os ideais têm fatoração única em ideais primos como os domínios de Dedekind: domínios integrais que são Noetheriano, 0 ou 1 dimensional, e integralmente fechado em seus campos de quociente. Este documento também contém o que hoje são chamados os teoremas de isomorfismo, que descrevem algumas fundamentais isomorfismos naturais, e alguns outros resultados básicos sobre noetherianos e módulos Artinian.
Teoria eliminação
Em 1923-1924, Noether aplicou sua teoria ideal para eliminação teoria em uma formulação que ela atribuiu a sua aluna, Kurt Hentzelt-mostrando que teoremas fundamentais sobre a fatoração de polinômios pode transitar diretamente. Tradicionalmente, teoria eliminação está preocupado com a eliminação de um ou mais variáveis a partir de um sistema de equações polinomiais, geralmente pelo método da resultantes. Para ilustração, o sistema de equações, muitas vezes pode ser escrito sob a forma de uma matriz M (faltando a variável X ) vezes um vector V (apenas ter diferentes potências de x ) igual a zero, o vector, M • v = 0 . Assim, o determinante de a matriz M deve ser zero, fornecendo uma nova equação em que a variável X foi eliminado.
Teoria dos invariantes de grupos finitos
Técnicas como a solução não-construtiva original de Hilbert para o problema base finita não poderia ser usado para obter informações quantitativas sobre as invariantes de uma ação do grupo, e, além disso, eles não se aplicam a todas as ações do grupo. Em seu papel de 1915, Noether encontrada uma solução para o problema base finita para um grupo finito de transformações G agindo em um espaço vetorial de dimensão finita sobre um campo de característica zero. A sua solução que mostra o anel de invariantes é gerado por invariantes homogéneos cujo grau é menor que, ou igual a, a ordem do grupo finito; isso é chamado, Noether do limite . Seu papel deu duas provas de Noether do encadernadas, sendo que ambos também trabalham quando a característica do campo é coprime a | G | !, o fatorial da ordem | G | do grupo G . O número de geradores não precisam de satisfazer de Noether ligado quando a característica do campo divide o | L |, mas Noether não foi capaz de determinar se o ligado foi correcta quando a característica do campo divide | L |! mas não | G |. Por muitos anos, determinando a verdade ou falsidade do limite, neste caso, era um problema em aberto chamado "gap de Noether". Ele finalmente foi resolvido independentemente por Fleischmann em 2000 e Fogarty, em 2001, que mostrou que tanto o limite mantém-se fiel.
Em seu papel de 1926, estendeu o teorema de Noether Hilbert para representações de um grupo finito sobre qualquer matéria; o novo processo, que não seguem a partir de trabalhos de Hilbert, é quando a característica do campo divide a ordem do grupo. Resultado de Noether foi posteriormente prorrogado por William Haboush a todos os grupos redutores por sua prova da conjectura Mumford. Neste trabalho Noether também introduziu o Noether normalização lema , mostrando que um finitamente gerado domínio Um sobre um campo de k tem um conjunto x 1 , ..., x n de elementos algebricamente independentes de tal forma que A é integral sobre k [ x 1 , ..., x n ] .
Contribuições para a topologia
Como observado por Pavel Alexandrov e Hermann Weyl em seus obituários, contribuições de Noether a topologia ilustrar sua generosidade com idéias e seus insights como poderia transformar campos inteiros de matemática. Em topologia, os matemáticos estudam as propriedades dos objetos que permanecem invariáveis, até sob deformação, propriedades, tais como a sua conectividade. Uma piada comum é que um topologist não pode distinguir um donut de uma caneca de café, uma vez que pode ser continuamente deformado em um outro.
Noether é creditado com as idéias fundamentais que levaram ao desenvolvimento da topologia algébrica da anterior topologia combinatória, especificamente, a idéia de grupos de homologia. De acordo com o relato de Alexandrov, Noether participaram de palestras dadas por Heinz Hopf e ele nos verões de 1926 e 1927, onde "ela continuamente feitas observações, que foram muitas vezes profundo e sutil" e que ele continua,
Quando ... ela primeiro tornou-se familiarizado com uma construção sistemática de topologia combinatória, ela observou imediatamente que seria interessante para estudar diretamente os grupos de complexos algébricas e ciclos de um determinado poliedro eo subgrupo do grupo ciclo constituído por ciclos homólogas zero; em vez de a definição usual de números de Betti, sugeriu imediatamente definindo o grupo Betti como o (quociente) grupo do grupo de todos os ciclos complementar pelo subgrupo de ciclos homóloga a zero. Esta observação agora parece auto-evidente. Mas naqueles anos (1925- 28 ), este foi um completamente novo ponto de vista.
A sugestão de que Noether topologia algébrica ser estudado, foi adotado imediatamente por Hopf, Alexandrov, e outros, e tornou-se um tópico frequente de discussão entre os matemáticos de Göttingen. Noether observou que sua idéia de um grupo Betti faz a fórmula de Euler-Poincaré mais simples de entender, eo trabalho próprio Hopf sobre este assunto "traz a marca dessas observações de Emmy Noether". Noether menciona suas próprias idéias de topologia apenas como um aparte em uma publicação 1926, onde ela cita-o como uma aplicação da teoria do grupo .
A abordagem algébrica para topologia foi desenvolvido de forma independente na Áustria . Em um curso 1926-1927 dada em Viena , Leopold Vietoris definiu um grupo de homologia, que foi desenvolvido por Walther Mayer, em uma definição axiomática em 1928.

Terceira época (1927-1935)
Hypercomplex números e teoria da representação
Muito trabalho em números hypercomplex e as representações do grupo foi realizada no século XIX e início do século XX, mas manteve-se díspares. Noether uniu os resultados e deu a primeira teoria da representação geral dos grupos e álgebras. Resumidamente, Noether subsumido a teoria da estrutura de álgebras associativas e da teoria da representação de grupos em uma única teoria aritmética dos módulos e ideais em anéis que satisfaçam as condições da cadeia ascendente. Este único trabalho de Noether foi de fundamental importância para o desenvolvimento da álgebra moderna.
Álgebra não-comutativa
Noether também foi responsável por uma série de outros avanços no campo da álgebra. Com Emil Artin,Richard Brauer, eHelmut Hasse, ela fundou a teoria deálgebras simples centrais.
Um papel seminal de Noether, Helmut Hasse, e Richard Brauer refere-se a álgebra de divisão, que são sistemas algébricos em que a divisão é possível. Eles provaram dois teoremas importantes: um teorema local-global afirmando que, se um dimensional álgebra divisão central finita sobre um campo de número se divide localmente em todos os lugares, em seguida, divide-se globalmente (por isso é trivial) e, a partir disso, deduzida a sua Hauptsatz ("teorema principal") : cada dimensão finita centro de álgebra divisão sobre um número algébrico campo F divide sobre uma extensão ciclotômico cíclico . Estes teoremas permitem classificar todos os dimensionais álgebras de divisão central finitos longo de um determinado campo de número. Um documento subsequente por Noether mostrou, como um caso especial de um teorema mais geral, que todos os subcampos máximas de uma divisão álgebra D são campos de divisão. Este documento também contém o teorema de Skolem-Noether, que afirma que quaisquer dois mergulhos de uma extensão de um campo de k em um dimensional álgebra simples centro finita sobre k , são conjugados. O Brauer-Noether teorema dá uma caracterização dos campos de divisão de uma divisão central álgebra sobre um campo.
Avaliação, reconhecimento e memoriais

O trabalho de Noether continua a ser relevante para o desenvolvimento da física teórica e matemática e ela é consistentemente classificado como um dos maiores matemáticos do século XX. Em seu obituário, companheiro algebraist BL van der Waerden diz que sua originalidade matemática era "absoluta além comparação", e Hermann Weyl disse que Noether "mudou a face da álgebra por seu trabalho ". Durante sua vida e mesmo até hoje, Noether foi caracterizado como o maior matemático mulher na história por matemáticos como Pavel Alexandrov, Hermann Weyl, e Jean Dieudonné.
Em uma carta ao The New York Times,Albert Einsteinescreveu:
No julgamento dos matemáticos vivos mais competentes, Fräulein Noether foi o matemático mais significativo criativo gênio, até agora produzido desde o ensino superior das mulheres começou. No reino da álgebra, em que os matemáticos mais talentosos têm sido ocupados por séculos, ela descobriu métodos que provaram ser de enorme importância no desenvolvimento da atual geração de matemáticos.
Em 2 de janeiro de 1935, poucos meses antes de sua morte, matemáticoNorbert Wiener escreveu que
Senhorita Noether é ... o maior matemático mulher que já viveu; e o maior cientista da mulher de qualquer espécie que vive agora, e um estudioso, pelo menos no plano de Madame Curie .
Em uma exposição em 1964Feira Mundial dedicado aomatemáticos modernos, Noether era a única mulher representada entre os matemáticos notáveis do mundo moderno.
Noether foi homenageado em vários memoriais,
- O Associação de Mulheres em Matemática detém uma Palestra Noether para homenagear as mulheres em matemática todos os anos; no seu panfleto de 2005 para o evento, a Associação caracteriza Noether como "um dos grandes matemáticos do seu tempo, alguém que trabalhou e lutou para que ela amava e acreditava. Sua vida e obra continuam a ser uma tremenda inspiração".
- Consistente com sua dedicação a seus alunos, aUniversidade de Siegen abriga seus departamentos de física matemática e em edifícios sobreo Campus Emmy Noether.
- A Fundação Alemã de Pesquisa (Deutsche Forschungsgemeinschaft) opera oPrograma de Emmy Noether, uma bolsa de estudos a concessão de financiamento para promissores jovens estudantes de pós-doutoramento nas suas futuras actividades de investigação e de ensino.
- Uma rua em sua cidade natal, Erlangen, foi nomeado após Emmy Noether e seu pai, Max Noether.
- O sucessor do ensino secundário frequentou em Erlangen foi renomeado comoo Emmy Noether escola.
Na ficção, Emmy Nutter, o professor de física em "O Deus de Patentes" por Ransom Stephens, baseia-se Emmy Noether
Longe de casa,
- A cratera Nother nolado mais distante da Lua é nomeado após ela.
- O 7001 Noether asteróide também é nomeado para Emmy Noether.
Lista de estudantes de doutorado
| Data | Nome do aluno | Título da tese e tradução Inglês | Universidade | Publicação | |
|---|---|---|---|---|---|
| 1911/12/16 | Falckenberg, Hans | Verzweigungen von Lösungen nichtlinearer Differentialgleichungen
| Erlangen | Leipzig 1912 | |
| 1916/03/04 | Seidelmann, Fritz | Die Gesamtheit der kubischen und mit biquadratischen Gleichungen Affekt bei beliebigem Rationalitätsbereich
| Erlangen | Erlangen 1916 | |
| 1925/02/25 | Hermann, Grete | Die Frage der endlich vielen Schritte in der Theorie der Polynomideale unter Benutzung nachgelassener Sätze von Kurt Hentzelt
| Göttingen | Berlim 1926 | |
| 1926/07/14 | Grell, Heinrich | Beziehungen zwischen den Idealen verschiedener Ringe
| Göttingen | Berlim 1927 | |
| 1927 | Doräte, Wilhelm | Über einem verallgemeinerten Gruppenbegriff
| Göttingen | Berlim 1927 | |
| morreu antes de defesa | Hölzer, Rudolf | Zur Theorie der primären Ringe
| Göttingen | Berlim 1927 | |
| 1929/06/12 | Weber, Werner | Idealtheoretische Deutung der Darstellbarkeit beliebiger natürlicher Zahlen durch quadratische Formen
| Göttingen | Berlim 1930 | |
| 1929/06/26 | Levitski, Jakob | Über vollständig reduzible Ringe und Unterringe
| Göttingen | Berlim 1931 | |
| 1930/06/18 | Deuring, Max | Zur Theorie der arithmetischen algebraischen Funktionen
| Göttingen | Berlim 1932 | |
| 1931/07/29 | Fitting, Hans | Zur Theorie der Automorphismenringe Abelscher Gruppen und ihr analogon bei nichtkommutativen Gruppen
| Göttingen | Berlim 1933 | |
| 1933/07/27 | Witt, Ernst | Riemann-Rochscher Satz und Zeta-Funktion im Hyperkomplexen
| Göttingen | Berlim 1934 | |
| 1933/12/06 | Tsen, Chiungtze | Algebren über Funktionenkörpern
| Göttingen | Göttingen 1934 | |
| 1934 | Schilling, Otto | Über gewisse Beziehungen der zwischen Arithmetik hyperkomplexer Zahlsysteme und algebraischer Zahlkörper
| Marburg | Braunschweig 1935 | |
| 1935 | Stauffer, Ruth | A construção de uma base normal de um campo de extensão separável | Bryn Mawr | Baltimore 1936 | |
| 1935 | Vorbeck, Werner | Nichtgaloissche Zerfällungskörper einfacher Systeme
| Göttingen | ||
| 1936 | Wichmann, Wolfgang | Anwendungen Der p-adischen Theorie im Nichtkommutativen
| Göttingen | Monatshefte für Mathematik und Physik(1936)44, 203-24. |
Temas matemáticos epônimos
|
|
|