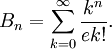Relação de equivalência

Em matemática , uma relação de equivalência é uma relação binária entre dois elementos de um definir quais os agrupa como sendo "equivalente" de alguma forma. Deixe-a, b, ec ser elementos arbitrários de algum conjunto X. Em seguida, "a b ~" ou "um ≡ b" indica que é equivalente a uma b.

Uma relação de equivalência "~" é reflexiva, simétrica , e transitivo. Em outras palavras, o seguinte deve ser verdadeira para "~" para ser uma relação de equivalência em X:

Uma relação de equivalência partições de um conjunto em vários subconjuntos disjuntos, chamado classes de equivalência. Todos os elementos de uma determinada classe de equivalência são equivalentes entre si, e nenhum elemento é equivalente com qualquer elemento de uma classe diferente.

• Reflexividade: a um ~
• Simetria: se uma b ~ b ~, em seguida, um
• Transitividade: se uma b ~ e b ~ c, em seguida, um c ~.

O uma classe de equivalência "~" sob, denotado [a], é o subconjunto de X, cujos elementos b são tais que um X ~ b. "~" em conjunto com um é chamado setoid.

Exemplos de relações de equivalência

A relação de equivalência é o onipresente igualdade ("=") relação entre elementos de qualquer conjunto. Outros exemplos incluem:

• "Tem o mesmo aniversário que" no conjunto de todas as pessoas, dado teoria dos conjuntos ingênua.
• "É semelhante ao" ou "congruentes com" sobre o conjunto de todos os triângulos .
• "É congruente com módulo n "sobre os números inteiros .
• "Tem o mesmo imagem sob uma função "sobre os elementos do domínio da função.
• Equivalência lógica de frases lógicas.
• "É isomorphic para "on modelos de um conjunto de frases.
• Em alguns conjunto teorias axiomáticas outros do que o canônico ZFE (por exemplo, Novas Fundações e teorias relacionadas):
  • Similaridade no universo de bem ordenamentos dá origem a classes de equivalência que são os números ordinais .
  • Equinumerosity no universo de:
    • Conjuntos finitos dá origem a classes de equivalência que são os números naturais .
    • Conjuntos infinitos dá origem a classes de equivalência que são o transfinitos números cardinais .
• Deixe a, b, c, d ser números naturais , e deixe (a, b) e (c, d) ser pares ordenados de tais números. Então o classes de equivalência sob a relação (a, b) ~ (c, d) são:
  • Inteiros se a + d = b + c;
  • Positivo números racionais se ad = bc.
• Seja (R _n) e _(n s) ser quaisquer dois Seqüências de Cauchy de números racionais. Os números reais são as classes de equivalência da relação (r _n) ~ (s _n), se a sequência (r _n - s _n) tem limite 0.
• Relações de Green são cinco relações de equivalência sobre os elementos de uma semigroup.
• "É paralelo ao "no set de subespaços de um espaço afim.

Exemplos de relações que não são equivalências

• A relação "≥" entre os números reais é reflexiva e transitiva, mas não simétrica. Por exemplo, 7 ≥ 5 não implica que 5 ≥ 7. É, no entanto, uma ordem parcial.
• A relação "tem um factor comum maior do que uma com" entre os números naturais maiores do que 1, é simétrica e reflexiva, mas não transitória. (Os números naturais 2 e 6 têm um factor comum maior do que 1, 6 e 3 e tem um factor comum maior do que 1, 2 e 3, mas não tem um factor comum maior do que 1).
• A relação R vazio em um não vazio conjunto X (ou seja aRb não é verdade) é vacuously simétrica e transitiva, mas não reflexiva. (Se X também está vazia, então R é reflexiva.)
• A relação "é aproximadamente igual" entre os números reais ou outras coisas, mesmo se mais precisamente definidas, não é uma relação de equivalência, porque embora reflexiva e simétrica, não é transitivo, uma vez que várias pequenas mudanças podem acumular-se a tornar-se uma grande mudança.
• A relação "é um irmão de" no conjunto de todos os seres humanos não é uma relação de equivalência. Embora germanidade é simétrica (se A é um irmão de B, então B é um irmão de A) não é nem reflexiva (ninguém é um irmão de si mesmo), nem transitivo (já que, se A é um irmão de B, então B é um irmão de A, mas A não é um irmão de A). Em vez de ser transitivo, germanidade é "quase transitivo", o que significa que, se A ~ B, e B ~ C, e A ≠ C, então A ~ C.
• O conceito de paralelismo em ordenada geometria não é simétrica e é, por conseguinte, não é uma relação de equivalência.
• Uma relação de equivalência em um conjunto nunca é uma relação de equivalência em um super adequada desse conjunto. Por exemplo R = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3, 2), (3,3)} é uma relação de equivalência em {1,2,3}, mas não em {1,2,3,4} ou em um número natural. O problema é que a reflexividade falha porque (4,4) não é um membro.

A conexão com outras relações

A relação de congruência é uma relação de equivalência cujo domínio X é também o conjunto de base para uma estrutura algébrica , e que respeita a estrutura adicional. Em geral, as relações de congruência desempenhar o papel de grãos de homomorphisms, e o quociente de uma estrutura por uma relação de congruência pode ser formado. Em muitos casos importantes relações de congruência ter uma representação alternativa como subestruturas da estrutura sobre a qual eles são definidos. Por exemplo, as relações de congruência em grupos correspondem ao subgrupos normais.

Ordem e de equivalência relações são ambos transitivo, mas apenas relações de equivalência são simétricas também. Se simetria está enfraquecido para antisimetría, o resultado é um ordem parcial.

A relação de equivalência parcial é transitivo e simétrica, mas não reflexiva.

• Transitivo e simétrica implica reflexiva sse para todo a, b ∈ X, a ~ b é sempre definido.
  

A relação de dependência é reflexiva e simétrica, mas não transitivo.
A pré-venda é reflexiva e transitiva, mas nem simétrico nem anti-simétrica.
A ordem parcial estrita é transitivo sozinho.

Relações de equivalência pode, assim, ser vista como o ápice de uma hierarquia de relações de ordem.

Classe de equivalência, conjunto quociente, partição

Seja X um nonempty conjunto com elementos típicos ae b. Algumas definições:

• O conjunto de todos a e b para os quais a ~ b detém compõem um classe de equivalência de X por ~. Deixe [a] =: {x ∈ X: x ~ a} denotar a classe de equivalência para que um pertence. Em seguida, todos os elementos de X equivalentes uns aos outros também são elementos da mesma classe de equivalência: ∀ a, b ∈ X (a b ~ ↔ [a] = [b]).
• O conjunto de todas as classes de equivalência possíveis de X por ~, denotado X / ~ =: {[x]: x ∈ X}, é a quociente de X definido por ~. Se X é um espaço topológico, há uma maneira natural de transformar X / ~ em um espaço topológico; ver espaço quociente para os detalhes.
• O projeção de ~ é o π função: X → X / ~, definida por π (x) = [x], elementos de mapeamento de X em suas respectivas classes de equivalência por ~.
  

Teorema sobre projeções (Birkhoff e Mac Lane 1999: 35, 19 Th.): Deixe a função f: X → B ser tal que a ~ b → f (a) = f (b). Depois, há uma única função g: X / ~ → B, tal que f = g π. Se f for um surjection e uma b ~ ↔ f (a) = f (b), então g é um bijection.

• O núcleo de equivalência de uma função f é a relação de equivalência, denotado Ef, de tal modo que xEfy ↔ f (x) = f (y). O núcleo de uma equivalência injecção é a relação de identidade.
• A partição de X é um grupo P de subconjuntos de X, de tal modo que cada elemento de X é um elemento de um único elemento de P. Cada elemento de P é uma célula da partição. Além disso, os elementos de P são disjuntos aos pares e sua união é X.

Teorema ("teorema fundamental de relações de equivalência": Wallace 1998:. 31, Th 8; Dummit e Foote 2004:. 3, Prop 2):

• Uma relação de equivalência ~ divisórias X.
• Por outro lado, correspondendo a qualquer partição de X, existe uma relação de equivalência ~ em X.

Em ambos os casos, as células da partição de X são as classes de equivalência de X por ~. Uma vez que cada elemento de X pertence a uma célula única de qualquer divisão do X, e desde que cada célula da partição é idêntica a uma classe de equivalência de X por ~, cada elemento de X pertence a uma classe de equivalência única de X por ~. Assim, há uma naturais bijection a partir do conjunto de todas as possíveis relações de equivalência em X eo conjunto de todas as partições de X.

Contando possíveis partições. Seja X um conjunto finito com n elementos. Uma vez que cada relação de equivalência sobre X corresponde a uma partição de X, e vice-versa, o número de possíveis relações de equivalência em X é igual ao número de partições distintas de X, que é o enésimo Sino número B _n:

Gerando relações de equivalência

• Dado qualquer conjunto X, existe uma relação de equivalência sobre o conjunto de todas as possíveis funções X → X. Dois de tais funções são consideradas equivalentes quando os respectivos conjuntos de pontos fixos têm a mesma cardinalidade, correspondendo a um comprimento de ciclos em uma permutação . Funções equivalentes desta maneira formar uma classe de equivalência em X ^2, e estas classes de equivalência partição X ^2.

• Uma relação de equivalência ~ em X é o kernel equivalência do seu surjective projecção π: X → X / ~. (Birkhoff e Mac Lane 1999: 33 18 Th.). Por outro lado, qualquer surjection entre conjuntos determina uma partição em sua domínio, o conjunto de preimages de únicos na codomain. Assim, uma relação de equivalência sobre X, uma partição de X, e uma projeção cujo domínio é X, são três maneiras equivalentes de especificar a mesma coisa.

• A intersecção de dois quaisquer relações de equivalência sobre X (vista como um subconjunto de X × X) é também uma relação de equivalência. Obteve-se uma maneira conveniente de gerar uma relação de equivalência: dada qualquer relação binária R em X, a relação de equivalência gerado por R é a menor relação de equivalência contendo R. Concretamente, R gera a relação de equivalência a ~ b sse existem elementos x _1, x _2, ..., x _n, em que X tal um x = _1, b = x _n, e (x _i, x _{i + 1)} ∈ R ou (x _{1 i,} x _i) ∈ R, i = 1, ..., n-1.

Note-se que a relação de equivalência gerado desta forma pode ser trivial. Por exemplo, a relação de equivalência ~ gerado por:

• A ≤ relação binária tem exatamente uma classe de equivalência, em si X, porque x ~ y para todos os x e y;
• Um relação antisymmetric tem classes de equivalência que são o singletons de x.

• Seja r qualquer tipo de relação em X. Então r ∪ r ^-1 é um relação simétrica. O transitivo encerramento de r ∪ s r ^-1 garante que s é transitivo e reflexiva. Além disso, s é a "menor" relação de equivalência que contém r, e r / s parcialmente ordens X / s.

• Relações de equivalência pode construir novos espaços por "colagem coisas juntos." Seja X a unidade Quadrado cartesiano [0,1] × [0,1], e deixar ~ ser a relação de equivalência em X definida por ∀ a, b ∈ [0,1] ((a, 0) ~ (a, 1) ∧ (0 , b) ~ (1, b)). Então o espaço quociente X / ~ pode ser naturalmente identificado com um toro : tirar um pedaço quadrado de papel, dobrar e colar em conjunto a aresta superior e inferior de modo a formar um cilindro, em seguida, dobrar o cilindro resultando assim como para colar em conjunto as suas duas extremidades abertas, resultando num toro .

Estrutura algébrica

Reticulados modulares

As possíveis relações de equivalência em qualquer conjunto X, quando ordenada pela inclusão conjunto , formam um estrutura modular, chamado Con X por convenção. O canônica mapa ker: X ∧ X → X Con, relata a monoid X ^ X de todas as funções no X e X Con. ker é surjective mas não injective. Menos formalmente, a ker relação de equivalência em X, leva cada função f: X → X a sua núcleo ker f. Da mesma forma, ker (ker) é uma relação de equivalência em X ^ X.

A teoria do grupo

É muito bem conhecido que teoria do retículo capta a estrutura matemática da relações de ordem. É menos conhecido que grupos de transformação (alguns autores preferem grupos de permutação) e sua órbitas lançar luz sobre a estrutura matemática de relações de equivalência. Assim como relações de ordem são baseadas em conjuntos ordenados, conjuntos fechados sob pairwise supremum e ínfimo, relações de equivalência são baseadas em conjuntos com partições, conjuntos fechados sob bijeções preservando a estrutura de partição. Uma vez que todos esses bijeções mapear uma classe de equivalência sobre si mesmo, tais bijeções são também conhecidos como permutações .

Deixe '~' denotam uma relação de equivalência sobre algum conjunto não-vazio A, chamado de universo ou conjunto subjacente. Seja G o conjunto de funções bijective sobre A que preservar a estrutura de partição de A: ∀ x ∈ A ∀ g ∈ G (g (x) ∈ [x]). Então, os seguintes três teoremas conectados segurar (Van Fraassen 1989: §10.3):

• ~ A partições em classes de equivalência. (Este é o teorema fundamental de relações de equivalência, mencionado acima);
• Dado um partição de A, G é um grupo transformação sob composição, cujas órbitas são o células da partição ‡;
• Dado um grupo transformação G sobre A, existe uma relação de equivalência ~ sobre A, cujas aulas são a equivalência órbitas de G. (Wallace 1998: 202, Th 6; Dummit e Foote 2004:. 114, Prop. 2).

Em suma, dada uma relação de equivalência sobre ~ A, existe uma grupo transformação g durante um cujas órbitas são as classes de equivalência de A sob ~.

Esta caracterização grupo transformação das relações de equivalência difere fundamentalmente a maneira Grades de caracterizar relações de ordem. Os argumentos das operações teoria do retículo conhecer e juntar são elementos de algum universo A. Enquanto isso, os argumentos das operações do Grupo transformação composição e inversa são elementos de um conjunto de bijeções, A → A.

Movendo-se para os grupos em geral, seja H um subgrupo de algum grupo L. Vamos ~ ser uma relação de equivalência em G, tal que uma b ~ ↔ (ab ^-1 ∈ H). As classes de equivalência de ~ -também chamado as órbitas da acção de H em G -são a direita cosets de H em G. Trocando a e b produz as classes laterais esquerdos.

Para saber mais sobre a teoria do grupo e relações de equivalência, consulte Lucas (1973: §31).

‡ Proof (adaptado de Van Fraassen 1989: 246). Vamos composição função interpretar multiplicação grupo e função inversa interpretar grupo inverso. Então G é um grupo sob a composição, o que significa que ∀ x ∈ A ∀ g ∈ G ([g (x)] = [x]), porque G satisfaz as quatro condições seguintes:

• G é fechada sob composição . A composição de quaisquer dois elementos de G existe, porque a e domínio codomain de qualquer elemento de G é um. Além disso, a composição é de bijeções bijective (Wallace 1998: 22, Th. 6);
• Existência de elemento de identidade. O função identidade, I (x) = x, é um elemento óbvio de G;
• Existência de função inversa . Cada função bijective g tem um inversa g ^-1, de tal modo que GG = ^-1 I;
• Composição associados . f (gh) = (fg) h. Isso vale para todas as funções mais todos os domínios (Wallace 1998:. 24, Th 7).

Sejam f e g haver quaisquer dois elementos do G. Em virtude da definição de L, [g (f (x))] = [f (x)] e [F (x)] = [x], de modo que [g (f (x))] = [X ]. Assim G também é um grupo de transformação (e um automorphism grupo) porque composição função preserva a partição de A.

Teoria Categoria

A composição de morphisms centrais teoria da categoria, denotada aqui por concatenação, generaliza a composição de funções centrais para grupos de transformação. Os axiomas da teoria da categoria afirmar que a composição do morfismos associados, e que à esquerda e à direita existem morphisms de identidade. Se todos os morphisms em um categoria deviam ter "inversas", a categoria se assemelharia a uma grupo transformação, cuja relação perto de relações de equivalência acaba de ser explicado. Um morfismo f pode-se dizer que o inverso quando f é um automorphism, ou seja, o e domínio codomain de F são idênticos, e existe um morfismo g de tal modo que morfismo fg = GF = identidade. Daí o conceito teórico-categoria mais próxima para uma relação de equivalência é uma categoria cuja morphisms são todos os automorfismos.

Relações de equivalência e lógica matemática

Relações de equivalência são uma fonte de exemplos ou contra-exemplos. Por exemplo, uma relação de equivalência com exatamente duas classes de equivalência infinitos é um exemplo fácil de uma teoria que é ω- categórica, mas não categórico para qualquer maior número cardinal .

Uma implicação teoria do modelo é que as propriedades que definem uma relação pode ser provada independente uns dos outros (e, portanto, necessárias partes da definição) se e somente se, para cada propriedade, podem ser encontrados exemplos de relações que não correspondam a propriedade dada, desde que satisfaçam todos os outros Propriedades. Daí a três definir propriedades de relações de equivalência pode ser provado independentes entre si pelas três exemplos a seguir:

• Reflexiva e transitiva: A relação ≤ em N. Ou qualquer pedido antecipado;
• Simétrica e transitiva: A relação R em N, definido como aRb ↔ ab ≠ 0. Ou qualquer relação de equivalência parcial;
• Reflexiva e simétrica: A relação R em Z, como definido aRb ↔ "a - b é divisível por, pelo menos, um dos 2 ou 3." Ou qualquer relação de dependência.

Características definidas na lógica de primeira ordem que uma relação de equivalência podem ou não possuir incluem:

• O número de classes de equivalência é finito ou infinito;
• O número de classes de equivalência é igual a (finitos) naturais número n;
• Todas as classes de equivalência têm infinito cardinalidade;
• O número de elementos em cada classe de equivalência é o número n natural.

Euclid equivalência antecipada

Euclides 's The Elements inclui o seguinte "noção comum de um":

Coisas que são iguais a mesma coisa também iguais entre si.

Hoje em dia, a propriedade descrita pela noção comum de um é chamado Euclidiana (substituindo "igual" por "estão em relação com"). Os seguintes Ligações teorema Relações euclidianas e relações de equivalência:

Teorema. Se a relação é euclidiana e reflexivo, que também é simétrica e transitória.

Prova:

• (ARC ∧ BRC) → aRb [a / c] = (ARA ∧ BRA) → aRb [reflexiva; apagar T ∧] = bRa → aRb. Daí R é simétrica .
• (ARC ∧ BRC) → aRb [simetria] = (ARC ∧ cRb) → aRb. Daí R é transitivo.

Daí uma relação de equivalência é uma relação que é euclidiana e reflexiva. O Elements menciona nem simetria nem reflexividade, e Euclid, provavelmente, teria considerado a reflexividade da igualdade óbvio demais para justificar uma menção explícita. Se esta (e tendo "igualdade" como uma relação abstrata para todos os fins) é concedido, uma leitura de caridade da noção comum de um gostaria crédito Euclid com ser o primeiro a conceber relações de equivalência e sua importância na sistemas dedutivos.