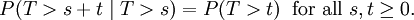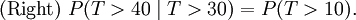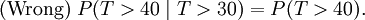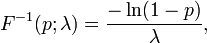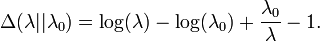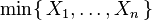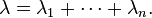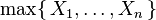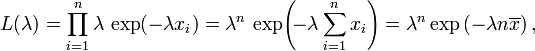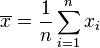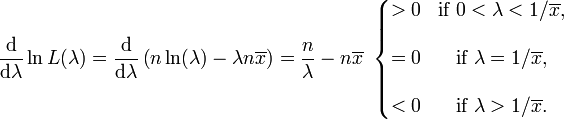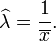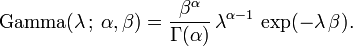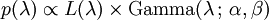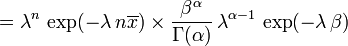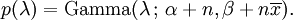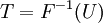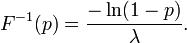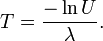Distribuição exponencial

Assuntos Relacionados: Matemática

Fundo para as escolas Wikipédia

Crianças SOS, uma instituição de caridade educação , organizou esta selecção. Com SOS Children você pode escolher para patrocinar crianças em mais de cem países

Exponencial
Função densidade de probabilidade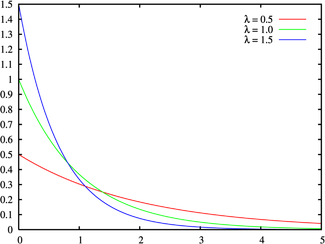
Função de distribuição cumulativa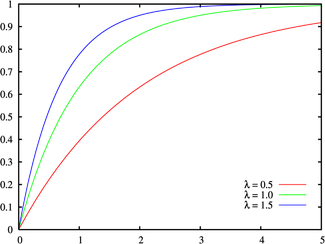
Parâmetros	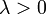$\ Lambda> 0 \,$ taxa ou escala inversa ( verdadeiro )
Apoio	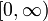$[0, \ infty) \!$
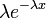PDF	$\ Lambda e ^ {- \ lambda x}$
CDF	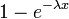$1 - e ^ {- \ lambda x}$
Significar	$\ Frac {1} {\ lambda} \,$
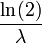Mediano	$\ Frac {\ ln (2)} {\ lambda} \,$
Modo	$0 \,$
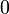Variação	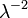$\ Lambda ^ {- 2} \,$
Assimetria	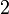$2 \,$
Ex. curtose	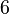$6 \,$
Entropy	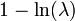$1 - \ ln (\ lambda) \,$
MGF	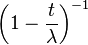$\ Left (1 - \ frac {t} {\ lambda} \ right) ^ {- 1} \,$
CF	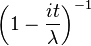$\ Left (1 - \ frac {ele} {\ lambda} \ right) ^ {- 1} \,$

Em teoria da probabilidade e estatística , a distribuição exponencial são uma classe de contínuas distribuições de probabilidade . Uma distribuição exponencial surge naturalmente ao modelar o tempo entre eventos independentes que acontecem a uma taxa média constante.

Caracterização

Função densidade de probabilidade

O função de densidade de probabilidade (pdf) de uma distribuição exponencial tem a forma

$f (x; \ lambda) = \ \ left {\ begin {matrix} \ lambda e ^ {- \ lambda x} e, \; x \ ge 0, \\ 0 &, \; x <0. \ end {matrix} \ right.$

onde λ> 0 é um parâmetro de distribuição, muitas vezes chamado o parâmetro da velocidade. A distribuição é suportado no intervalo [0, ∞). Se uma variável aleatória X tem essa distribuição, escrevemos X ~ Exponencial (λ).

Função de distribuição cumulativa

O função de distribuição cumulativa é dada por

$F (x; \ lambda) = \ \ left {\ begin {matrix} 1-e ^ {- \ lambda x} e, \; x \ ge 0, \\ 0 &, \; x <0. \ end {matrix} \ right.$

Parametrização alternativo

A parametrização alternativa utilizada é para definir o função densidade de probabilidade (pdf) de uma distribuição exponencial como

$f (x; \ beta) = \ \ left {\ begin {matrix} \ frac {1} {\ beta} e ^ {- x / \ beta} & \; x \ ge 0, \\ 0 &, \; x <0. \ end {matrix} \ right.$

onde β> 0 é um parâmetro de escala da distribuição e é a recíproco do parâmetro da velocidade, λ, definido acima. Na presente memória descritiva, é um parâmetro β sobrevivência no sentido de que se uma variável aleatória X representa a duração de tempo em que um determinado sistema biológico ou mecânico H consegue sobreviver e X ~ exponencial (β) seguida $\ Mathbb {E} [X] = \ beta$ . Isto é, a duração de sobrevivência esperada de unidades M é β de tempo.

Esta especificação alternativo às vezes é mais conveniente do que o dado acima, e alguns autores vão usá-lo como uma definição padrão. Nós não assumirá esta especificação alternativa. Infelizmente, isso dá origem a um ambigüidade de notação. Em geral, o leitor deve verificar qual destas duas especificações está sendo usado se um autor escreve "X ~ Exponencial (λ)", uma vez que tanto a notação da anterior (usando λ) ou a notação nesta seção (aqui, usando β para evitar confusão) poderia ser prevista.

Ocorrência e aplicações

A distribuição exponencial ocorre naturalmente ao descrever os comprimentos dos tempos entre chegadas num homogénea Processos de Poisson.

A distribuição exponencial pode ser visto como um homólogo contínua do distribuição geométrica, que descreve o número de Tentativas de Bernoulli necessárias para um processo discreto para mudar de estado. Em contraste, a distribuição exponencial descreve o tempo para um processo contínuo para alterar o estado.

Em cenários do mundo real, a hipótese de uma taxa constante (ou probabilidade por unidade de tempo) é raramente satisfeita. Por exemplo, a taxa de chamadas telefônicas de entrada difere de acordo com a hora do dia. Mas, se nos concentramos em um intervalo de tempo durante o qual a taxa é mais ou menos constante, como 2-4 horas durante os dias de trabalho, a distribuição exponencial pode ser usado como um bom modelo aproximado para o tempo até o próximo telefonema chega. Ressalvas semelhantes aplicam-se aos exemplos seguintes que produzem variáveis aproximadamente distribuídos exponencialmente:

o tempo até que uma partícula decai radioactivos, ou o tempo entre os sinais sonoros de uma contador Geiger;
o tempo que leva antes de sua próxima chamada telefônica
o tempo até padrão (no pagamento aos detentores de dívida da empresa) em forma reduzida de modelagem de risco de crédito

Variáveis exponenciais também pode ser utilizado para modelar situações em que certos eventos ocorrem com uma probabilidade constante por unidade de distância:

a distância entre mutações num DNA cadeia;
a distância entre atropelamentos em uma determinada rua;

Em teoria das filas, os tempos entre chegadas (ou seja, os tempos entre os clientes que entram no sistema) são muitas vezes modelado variáveis como exponencialmente distribuídos. O comprimento de um processo que pode ser pensado como uma sequência de várias tarefas independentes é melhor modelada por uma variável após a Distribuição Erlang (que é a distribuição da soma de diversas variáveis distribuídos exponencialmente independentes).

Teoria e confiabilidade engenharia de confiabilidade também fazem uso extensivo da distribuição exponencial. Devido à memoryless propriedade desta distribuição, que é bem adequado para modelar a constante parcela taxa de risco da curva da banheira usado em teoria fiabilidade. Também é muito conveniente, porque é tão fácil de adicionar taxas de falha em um modelo de confiabilidade. A distribuição exponencial não é, porém, adequado para modelar o tempo de vida global de organismos ou dispositivos técnicos, pois as "taxas de insucesso" aqui não são constantes: mais falhas ocorrem por muito jovem e para sistemas muito antigos.

Em física , se você observar um gás em um fixo de temperatura e pressão em um uniforme campo gravitacional, as alturas das várias moléculas também seguir uma distribuição exponencial aproximada. Esta é uma consequência da propriedade entropia mencionados abaixo.

Propriedades

Média e variância

A média ou valor esperado de uma variável aleatória X exponencialmente distribuído com o parâmetro da taxa de λ é dado por

$\ Mathrm {E} [X] = \ frac {1} {\ lambda}. \!$

À luz dos exemplos dados acima, isso faz sentido: se você receber chamadas de telefone em uma taxa média de 2 por hora, então você pode esperar de esperar meia hora para cada chamada.

A variância de X é dada pela

$\ Mathrm {var} [X] = \ frac {1} {\ lambda ^ 2}. \!$

Memorylessness

Uma propriedade importante da distribuição exponencial é que é sem memória. Isto significa que, se uma variável aleatória T é distribuído exponencialmente, o seu obedece probabilidade condicional

$P (T> s + t \; | \; T> s) = P (T> t) \; \; \ Hbox {para todo} \ s, t \ ge 0.$

Este diz que o probabilidade condicional de que precisamos de esperar, por exemplo, mais de mais 10 segundos antes da primeira chegada, uma vez que a primeira chegada ainda não aconteceu depois de 30 segundos, não é diferente de a probabilidade inicial que temos de esperar mais de 10 segundos para a primeira chegada. Este é muitas vezes incompreendido por estudantes de cursos sobre a probabilidade: o fato de que P (T> 40 | T> 30) = P (T> 10) não significa que os eventos T> 40 e T> 30 são independente. Para resumir: "memorylessness" da distribuição de probabilidade de o tempo de espera T até os primeiros meios de chegada

$\ Mathrm {(Direito)} \ P (T> 40 \ meados T> 30) = P (T> 10).$

Isso não significa

$\ Mathrm {(errada)} \ P (T> 40 \ meados T> 30) = P (T> 40).$

(Isso seria independência. Estes dois eventos não são independentes.)

As distribuições exponenciais e o distribuições geométricas são as únicas distribuições de probabilidade sem memória.

A distribuição exponencial também tem uma constante função de risco.

Quartis

A função quantil (função de distribuição cumulativa inversa) para Exponencial (λ) é

$F ^ {- 1} (p; \ lambda) = \ frac {- \ ln (1-p)} {\ lambda}, \!$

para 0 ≤ p <1. A quartis são, portanto:

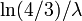
primeiro quartil: $\ Ln (4/3) / \ lambda \,$
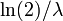
mediano: $\ Ln (2) / \ lambda \,$
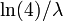
terceiro quartil: $\ Ln (4) / \ lambda \,$

Kullback-Leibler divergência

O dirigidos Kullback-Leibler divergência entre Exp (λ ₀₎ (distribuição 'true') e Exp (λ) («aproximação» de distribuição) é dada por

$\ Delta (\ lambda || \ lambda_0) = \ log (\ lambda) - \ log (\ lambda_0) + \ frac {\ lambda_0} {\ lambda} - 1.$

Distribuição máxima entropia

Entre todas as distribuições de probabilidades contínuas com suporte [0, ∞) e μ dizer, a distribuição exponencial com λ = 1 / μ tem o O maior entropia.

Distribuição do mínimo de variáveis aleatórias exponenciais

Deixe-X _1, ..., X _n ser variáveis aleatórias independentes exponencialmente distribuídos com parâmetros de taxa λ _1, ..., λ _n. Em seguida

$\ Min \ {\, X_1, \ pontos, X_n \, \}$

também é distribuído exponencialmente, com o parâmetro

$\ Lambda = \ lambda_1 + \ cdots + \ lambda_n. \,$

No entanto,

$\ Max \ {\, X_1, \ pontos, X_n \, \}$

não é distribuído exponencialmente.

Estimação de parâmetros

Suponha que você sabe que uma determinada variável é distribuído exponencialmente e que pretende estimar o parâmetro de taxa λ.

Máxima verossimilhança

O função de verossimilhança para λ, dado um amostra independente e identicamente distribuída x = (x _1, ..., x _n) retirados de sua variável, é

$L (\ lambda) = \ Prod_ {i = 1} ^ n \ lambda \, \ exp (- \ lambda x_i) = \ lambda ^ n \, \ exp \ \ left (\ -! \ Lambda \ sum_ {i = 1} ^ n x_i \ right) = \ lambda ^ n \ exp \ left (- \ lambda n \ overline {x} \ right),$

onde

$\ Overline {x} = {1 \ over n} \ sum_ {i = 1} ^ n x_i$

é a média da amostra.

O derivado do logaritmo da função de verossimilhança é

$\ Frac {\ mathrm {d}} {\ mathrm {d} \ lambda} \ ln L (\ lambda) = \ frac {\ mathrm {d}} {\ mathrm {d} \ lambda} \ left (n \ ln (\ lambda) - \ lambda n \ overline {x} \ right) = {n \ over \ lambda} -n \ overline {x} \ \ \ left {\ begin {matrix}> 0 & \ mbox {if} \ 0 <\ lambda <1 / \ overline {x}, \\ \\ = 0 & \ mbox {if} \ \ lambda = 1 / \ overline {x}, \\ \\ <0 & \ mbox {if} \ \ lambda> 1 / \ overline {x}. \ End {matrix} \ right.$

Por conseguinte, a estimativa de máxima verossimilhança para o parâmetro de taxa é

$\ Widehat {\ lambda} = \ frac1 {\ overline {x}}.$

Inferência Bayesiana

O conjugado prévia para a distribuição exponencial é o distribuição gama (da qual a distribuição exponencial é um caso especial). O seguinte parametrização da gama pdf é útil:

$\ Mathrm {Gamma} (\ lambda \,; \, \ alpha, \ beta) = \ frac {\ beta ^ {\ alpha}} {\ Gamma (\ alpha)} \, \ lambda ^ {\ alpha-1} \, \ exp (- \ lambda \, \ beta). \!$

O distribuição posterior p pode então ser expressa em termos da função de probabilidade definido acima e um gama anterior:

$p (\ lambda) \ propto L (\ lambda) \ times \ mathrm {Gamma} (\ lambda \,; \, \ alpha, \ beta)$

$= \ Lambda ^ n \, \ exp (- \ lambda \, n \ overline {x}) \ times \ frac {\ beta ^ {\ alpha}} {\ Gamma (\ alpha)} \, \ lambda ^ {\ alfa-1} \, \ exp (- \ lambda \, \ beta)$

$\ Propto \ lambda ^ {(\ alpha + n) -1} \, \ exp (- \ lambda \, (\ beta + n \ overline {x})).$

Agora, a densidade p posterior foi especificado acima para uma constante de normalização em falta. Uma vez que tem a forma de uma gama de PDF, isto pode facilmente ser preenchido, e obtém-se

$p (\ lambda) = \ mathrm {Gamma} (\ lambda \,; \, \ alpha + n, \ beta + n \ overline {x}).$

Aqui, os parâmetros α pode ser interpretado como o número de observações anteriores, e β como a soma das observações anteriores.

Gerando variates exponenciais

Um método conceptualmente muito simples para a geração exponencial variates baseia-se transformação inversa de amostragem: Dado um variate aleatório U retirados do distribuição uniforme no intervalo unitário 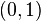$(0, 1)$ , O variate

$T = F ^ {- 1} (U) \!$

tem uma distribuição exponencial, onde 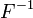$F ^ {- 1}$ é a função quantil, definido pela

$F ^ {-} 1 (p) = \ frac {- \ ln (1-P)} {\ lambda}. \!$

Além disso, se U é uniforme sobre 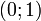$(0; 1)$ , Então é assim 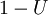$1-L$ . Isto significa que se pode gerar variates exponenciais como se segue:

$T = \ frac {- \ ln U} {\ lambda}. \!$

Outros métodos para gerar variates exponenciais são discutidos por Knuth e Devroye.

O algoritmo zigurate é um método rápido para a geração de variates exponenciais.

Distribuições relacionados

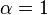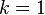Uma distribuição exponencial é um caso especial de um distribuição gama com $\ Alfa = 1$ (Ou $k = 1$ dependendo do conjunto de parâmetros utilizados).
Ambos uma distribuição exponencial e uma distribuição gama são casos especiais da distribuição do tipo fase.
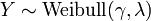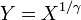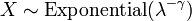$Y \ sim \ operatorname {} Weibull (\ gamma, \ lambda)$ , Isto é, Y tem um Distribuição de Weibull, se $Y = X ^ {1 / \ gamma} \,$ e $X \ sim \ operatorname {} Exponencial (\ lambda ^ {- \ gamma})$ . Em particular, cada distribuição exponencial é também uma distribuição de Weibull.
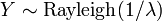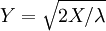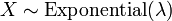$Y \ sim \ operatorname {} Rayleigh (1 / \ lambda)$ , Isto é, Y tem um Distribuição de Rayleigh, se $Y = \ sqrt {2X / \ lambda}$ e $X \ sim \ operatorname {} Exponencial (\ lambda)$ .
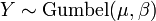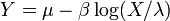$Y \ sim \ operatorname {} Gumbel (\ mu, \ beta)$ , Isto é, Y tem um Distribuição Gumbel se $Y = \ mu - \ beta \ log (/ \ lambda X) \,$ e $X \ sim \ operatorname {} Exponencial (\ lambda)$ .
$Y \ sim \ operatorname {Laplace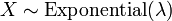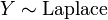}$ , Isto é, Y tem um Distribuição de Laplace, se 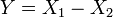$Y = X_1 - X_2 \,$ para dois distribuições exponenciais independentes 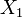$X_1 \,$ e $X_2 \,$ .
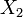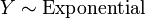$Y \ sim \ operatorname {exponencial}$ , Isto é, Y tem uma distribuição exponencial se 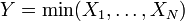$Y = \ min (x_1, \ dots, x_n)$ para distribuições exponenciais independentes $X_i \,$ .
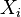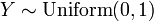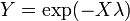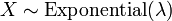$Y \ sim \ operatorname {} Uniforme (0,1)$ , Isto é, Y tem um distribuição uniforme se $Y = \ exp (X \ lambda) \,$ e $X \ sim \ operatorname {} Exponencial (\ lambda)$ .
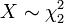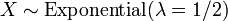$X \ sim \ chi_2 ^ 2$ , Ou seja, X tem uma distribuição qui-quadrado com 2 graus de liberdade, se $X \ sim \ operatorname {} Exponencial (\ lambda = 1/2) \, \;$ .
Deixar 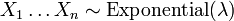$X_1 \ pontos X_n \ sim \ operatorname {} Exponencial (\ lambda) \,$ ser distribuído exponencialmente e independente e 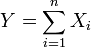$Y = \ sum_ {i = 1} ^ n x_i \,$ . Em seguida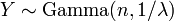 $Y \ sim \ operatorname {} Gamma (n, 1 / \ lambda) \,$
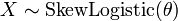$X sim \ operatorname {SkewLogistic} (\ theta) \ \,$ , Então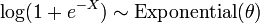 $\ Operatorname {} log (1 + e ^ {- X}) \ sim \ operatorname {} Exponencial (\ theta) \,$