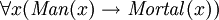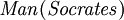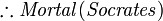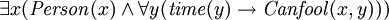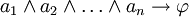Lógica de primeira ordem
Você sabia ...
Crianças SOS, uma instituição de caridade educação , organizou esta selecção. Crianças SOS é a maior doação de caridade do mundo órfãos e crianças abandonadas a chance da vida familiar.
De primeira ordem lógica (FOL) é um formais sistema dedutivo usado por matemáticos, filósofos, lingüistas e cientistas da computação. Ele vai por muitos nomes, incluindo: cálculo de primeira ordem predicado (FOPC), o cálculo de predicados inferior, a linguagem da lógica de primeira ordem ou lógica de predicados. Diferentemente das linguagens naturais, como Inglês, FOL usa um totalmente inequívoca linguagem formal interpretado por estruturas matemáticas. FOL é um sistema de dedução estendendo lógica proposicional, permitindo a quantificação sobre os indivíduos de um determinado domínio (universo) do discurso. Por exemplo, pode-se afirmar em FOL "Toda a pessoa tem a propriedade P".
Enquanto Lógica Proposicional lida com simples proposições declarativas, lógica de primeira ordem, adicionalmente, tampas predicados e quantificação. Tomemos por exemplo as seguintes frases: "Sócrates é um homem", "Platão é um homem". Na lógica proposicional estes serão duas proposições independentes, denotados por exemplo, p e q. Em primeira ordem lógica no entanto, ambas as sentenças seriam ligados pela mesma propriedade: Man (x), onde Man (x) significa que x é um homem. Quando x = Sócrates chegarmos a primeira proposição, p, e quando x = Platão ficamos com a segunda proposição, q. Uma tal construção permite que para uma lógica muito mais potente quando quantificadores são introduzidas, tais como "para cada X ...", por exemplo, "para cada X, se o Homem (x), em seguida, ...". Sem quantificadores, cada argumento válido em FOL é válida em lógica proposicional, e vice-versa.
A teoria de primeira ordem é composto por um conjunto de axiomas (geralmente finito ou recursivamente enumeráveis) e as demonstrações dedutível dado a eles a relação dedutibilidade subjacente. Normalmente o que se entende por "teoria de primeira ordem 'é um conjunto de axiomas, juntamente com os de um (e som) axiomatization completa de lógica de primeira ordem, fechado sob as regras do FOL. (Qualquer sistema deste tipo FOL dará origem à mesma relação abstrata dedutibilidade, por isso, não precisa ter um sistema axiomático fixo em mente.) A linguagem de primeira ordem tem poder expressivo suficiente para formalizar duas teorias matemáticas importantes: ZFC teoria dos conjuntos e Aritmética de Peano. A linguagem de primeira ordem não pode, no entanto, expressar categoricamente a noção de enumerabilidade mesmo que seja expressável na teoria de primeira ordem ZFE sob a interpretação destinado do simbolismo da ZFC. Tais idéias podem ser expressas com categoricamente lógica de segunda ordem.
Porque é que a lógica de primeira ordem necessária?
A lógica proposicional não é adequada para formalizar argumentos válidos que dependem da estrutura interna das proposições envolvidas. Para ver isto, considere o válido argumento silogístico:
- Todos os homens são mortais
- Sócrates é um homem
- Portanto, Sócrates é mortal
que quando da tradução em rendimentos lógica proposicional:
- A
- B
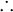 C
C
(Tomada 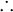 para significar "portanto").
para significar "portanto").
De acordo com a lógica proposicional, esta tradução é inválido: lógica proposicional valida argumentos de acordo com a sua estrutura, e nada na estrutura deste argumento traduzido (C Decorre A e B, por arbitrária A, B, C) sugere que ele é válido. Uma tradução que preserva a validade intuitiva (e formal) do argumento deve levar em consideração a estrutura mais profunda de proposições, como as noções essenciais de predicação e quantificação. Lógica Proposicional trata apenas de validade verdade-funcional: qualquer atribuição de valores de verdade para as variáveis do argumento deve fazer qualquer conclusão verdadeira ou, pelo menos, uma das premissas falsas. É claro que pode (uniformemente) atribuir valores de verdade para as variáveis do argumento acima tal que A, B são verdadeiras, mas C é falsa. Por isso, o argumento é verdade funcionalmente inválido. Por outro lado, é impossível (uniformemente) atribuir valores verdade no argumento de "Um segue de (A e B)" tal que (A e B) é verdade (daí Uma é verdadeira e B é verdade) e A falsa .
Em contrapartida, este argumento pode ser facilmente traduzida em lógica de primeira ordem:
(Onde " 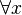 "Significa" para todos os x ","
"Significa" para todos os x ","  "Significa" implica ",
"Significa" implica ", 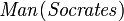 significa "Sócrates é um homem", e
significa "Sócrates é um homem", e 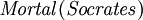 significa "Sócrates é mortal".) Na planície Inglês, este afirma que
significa "Sócrates é mortal".) Na planície Inglês, este afirma que
- para todo x, se x é um homem, então x é mortal
- Sócrates é um homem
- portanto, Sócrates é mortal
FOL também pode expressar a existência de algo ( 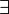 ), Bem como predicados ("funções" que são verdadeiras ou falsas) com mais do que um parâmetro. Por exemplo, "há alguém que pode ser enganado cada vez" pode ser expressa como:
), Bem como predicados ("funções" que são verdadeiras ou falsas) com mais do que um parâmetro. Por exemplo, "há alguém que pode ser enganado cada vez" pode ser expressa como:
Onde " 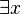 "Significa" não existe (a) x ","
"Significa" não existe (a) x "," 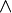 "Significa" e ", e
"Significa" e ", e 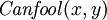 meios "(pessoa) x pode ser enganado (no momento) y".
meios "(pessoa) x pode ser enganado (no momento) y".
Definição de primeira ordem lógica
Um cálculo de predicados consiste em
- regras de formação (isto é, definições recursivas para a formação fórmulas bem formadas).
- regras de transformação (isto é, regras de inferência para derivar teoremas).
- axiomas ou axioma esquemas (possivelmente infinito contável).
Os axiomas aqui considerados são axiomas lógicos que fazem parte da FOL clássica. É importante notar que FOL pode ser formalizado em muitas maneiras equivalentes; não há nada canônica sobre os axiomas e regras de inferência dadas neste artigo. Há um número infinito de formalizações equivalentes todos os que produzem os mesmos teoremas e não-teoremas, e todos os que têm igual direito ao título "FOL".
FOL é usado como o "bloco de construção" fundamental para muitas teorias matemáticas. FOL fornece várias regras internas, como o axioma 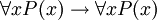 (Se P (x) é verdadeiro para cada x então P (x) é verdadeiro para cada x). Axiomas não-lógicos adicionais são adicionados para produzir teorias de primeira ordem específicas com base nos axiomas da FOL clássica; essas teorias desenvolvidas a partir FOL são chamados teorias de primeira ordem clássicas. Um exemplo de uma teoria de primeira ordem é clássica Aritmética de Peano, que acrescenta ao axioma
(Se P (x) é verdadeiro para cada x então P (x) é verdadeiro para cada x). Axiomas não-lógicos adicionais são adicionados para produzir teorias de primeira ordem específicas com base nos axiomas da FOL clássica; essas teorias desenvolvidas a partir FOL são chamados teorias de primeira ordem clássicas. Um exemplo de uma teoria de primeira ordem é clássica Aritmética de Peano, que acrescenta ao axioma 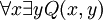 (Ou seja, para cada x existe y tal que y = x + 1, em que Q (x, y) é interpretado como "y = x + 1"). Este axioma adicional é um axioma não-lógico; ele não faz parte do FOL, mas em vez disso é um axioma da teoria (um axioma de aritmética do que de lógica). Axiomas do último tipo são também chamados de axiomas de teorias de primeira ordem. Os axiomas de teorias de primeira ordem não são consideradas como verdades da lógica em si, mas sim como verdades da teoria em particular, que geralmente tem associado a ele uma interpretação a que se destinam de seus símbolos não-lógicos. (Veja uma idéia análoga à lógica contra símbolos não lógico.) Assim, o axioma sobre Q (x, y) é verdadeira somente com a interpretação da relação Q (x, y) como "y = x + 1", e apenas na teoria de Aritmética de Peano. FOL clássico não tem associado a ele uma interpretação pretendido de seu vocabulário não-lógico (exceto possivelmente um símbolo que denota identidade, consoante se refere a uma tal símbolo tão lógico). set-A teoria clássica é outro exemplo de uma teoria de primeira ordem (uma teoria construída em FOL).
(Ou seja, para cada x existe y tal que y = x + 1, em que Q (x, y) é interpretado como "y = x + 1"). Este axioma adicional é um axioma não-lógico; ele não faz parte do FOL, mas em vez disso é um axioma da teoria (um axioma de aritmética do que de lógica). Axiomas do último tipo são também chamados de axiomas de teorias de primeira ordem. Os axiomas de teorias de primeira ordem não são consideradas como verdades da lógica em si, mas sim como verdades da teoria em particular, que geralmente tem associado a ele uma interpretação a que se destinam de seus símbolos não-lógicos. (Veja uma idéia análoga à lógica contra símbolos não lógico.) Assim, o axioma sobre Q (x, y) é verdadeira somente com a interpretação da relação Q (x, y) como "y = x + 1", e apenas na teoria de Aritmética de Peano. FOL clássico não tem associado a ele uma interpretação pretendido de seu vocabulário não-lógico (exceto possivelmente um símbolo que denota identidade, consoante se refere a uma tal símbolo tão lógico). set-A teoria clássica é outro exemplo de uma teoria de primeira ordem (uma teoria construída em FOL).
Vocabulário
Antes de configurar as regras de formação, é preciso descrever o "vocabulário", que é composto de
- Um conjunto de variáveis de predicados (ou relações) cada um com alguns valência (ou arity, número de seus argumentos) ≥1, que muitas vezes são representados por letras maiúsculas P, Q, R, ....
- Por exemplo, P (x) é uma variáveis de predicados de valência 1. Pode significam "x é um homem", por exemplo.
- Q (x, y) é uma variáveis de predicados de valência 2. Pode significam "x é maior que y" na aritmética ou "x é o pai de y", por exemplo.
- É possível permitir que as relações de valência 0; estes podem ser considerados variáveis proposicionais. Por exemplo, P, que pode ficar para qualquer instrução.
- Ao utilizar funções (ver abaixo), é possível dispensar com todas as variáveis de predicados com valência maior do que um. Por exemplo, "x> y" (um predicado de valência 2, do tipo Q (x, y)) pode ser substituído por um predicado de valência 1 sobre o par ordenado (x, y).
- Um conjunto de constantes, frequentemente designados por letras minúsculas no início do alfabeto a, b, c, ....
- Exemplos: um pode estar para Sócrates. Em aritmética , pode estar para 0. Em teoria dos conjuntos , tal constante pode ficar para o conjunto vazio.
- Um conjunto de funções, cada uma de cerca de valência ≥ 1, que são frequentemente designados por letras minúsculas F, G, H, ....
- Exemplos: f (x) pode estar para "o pai de x". Em aritmética , pode ficar por "-x". Na teoria dos conjuntos , pode estar para "o x conjunto de poder ". Em aritmética , f (x, y) pode estar para "x + y". Em teoria dos conjuntos , pode significar "a união de x e y".
- Uma constante é realmente uma função de valência 0. No entanto, é comum usar o termo "função" apenas para as funções de valência, pelo menos, 1.
- Pode-se, em princípio, dispensar inteiramente com funções de aridade> 2 e predicados de aridade> 1 se houver um símbolo de função de aridade 2 representa um par ordenado (ou símbolos de predicado de aridade 2 que representam as relações de projeção de um par ordenado). O par ou projeções precisa para satisfazer os axiomas naturais.
- Pode-se, em princípio, dispensar inteiramente todas as funções e constantes. Por exemplo, em vez de usar uma constante 0 pode-se utilizar um predicado 0 (x) (interpretada como "x = 0"), e substituir todos os predicados, tais como P (0, y) com
 x 0 (x)
x 0 (x)  P (x, y). Uma função como f (x 1, x 2 ...) da mesma forma, ser substituído por um predicado F (X1, X2 ..., y) (interpretada como "y = f (x 1, x 2 ...)").
P (x, y). Uma função como f (x 1, x 2 ...) da mesma forma, ser substituído por um predicado F (X1, X2 ..., y) (interpretada como "y = f (x 1, x 2 ...)").
- Um número infinito de variáveis, muitas vezes indicada por letras minúsculas na extremidade do alfabeto x, y, z, ....
- Símbolos que denotem operadores lógicos (ou conectivos):
 ( não é lógico),
( não é lógico),  ( lógica condicional).
( lógica condicional).  (Φ
(Φ 
 ψ) é logicamente equivalente a φ
ψ) é logicamente equivalente a φ 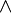 ψ ( lógico e). φ
ψ ( lógico e). φ 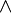 ψ pode ser visto como uma forma abreviada para esta. Alternativamente, pode-se adicionar o
ψ pode ser visto como uma forma abreviada para esta. Alternativamente, pode-se adicionar o 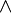 símbolo como um operador lógico para o vocabulário, e axiomas apropriados.
símbolo como um operador lógico para o vocabulário, e axiomas apropriados.  φ
φ  ψ é logicamente equivalente a φ
ψ é logicamente equivalente a φ 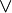 ψ ( lógico ou). φ
ψ ( lógico ou). φ 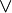 ψ pode ser visto como uma forma abreviada para esta. Alternativamente, pode-se adicionar o
ψ pode ser visto como uma forma abreviada para esta. Alternativamente, pode-se adicionar o 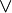 símbolo como um operador lógico para o vocabulário, e axiomas apropriados.
símbolo como um operador lógico para o vocabulário, e axiomas apropriados. - Do mesmo modo, (φ
 ψ)
ψ) 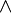 (Ψ
(Ψ  φ) é logicamente equivalente a φ
φ) é logicamente equivalente a φ 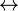 ψ ( bicondicional lógica), e pode-se usar este último como um atalho para isso, ou, alternativamente, inclua isto no vocabulário e acrescentar axiomas apropriados. Às vezes, φ
ψ ( bicondicional lógica), e pode-se usar este último como um atalho para isso, ou, alternativamente, inclua isto no vocabulário e acrescentar axiomas apropriados. Às vezes, φ 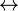 ψ é escrito como φ
ψ é escrito como φ  ψ.
ψ.
- Símbolos que denotem quantificadores:
 ( quantificação universal, normalmente lido como "para todos").
( quantificação universal, normalmente lido como "para todos"). 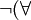 x
x  φ) é logicamente equivalente a
φ) é logicamente equivalente a 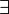 x φ ( quantificação existencial, normalmente lido como "existe"). Este último pode ser utilizado como uma abreviatura para esta, ou adicionado ao vocabulário juntamente com axiomas apropriados.
x φ ( quantificação existencial, normalmente lido como "existe"). Este último pode ser utilizado como uma abreviatura para esta, ou adicionado ao vocabulário juntamente com axiomas apropriados.
- Parênteses esquerdo e direito.
- Há muitas convenções diferentes sobre onde colocar parênteses; por exemplo, pode-se escrever
 x ou (
x ou (  x). Às vezes se usa dois pontos ou pontos em vez de parênteses para fazer fórmulas inequívoca. Uma convenção interessante, mas é bastante incomum " Notação polonês ", onde se omite todos os parênteses, e escreve
x). Às vezes se usa dois pontos ou pontos em vez de parênteses para fazer fórmulas inequívoca. Uma convenção interessante, mas é bastante incomum " Notação polonês ", onde se omite todos os parênteses, e escreve  ,
, 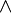 E assim por diante na frente de seus argumentos em vez de entre eles. Notação polonês é compacto e elegante, mas raro, porque é difícil para os seres humanos para lê-lo.
E assim por diante na frente de seus argumentos em vez de entre eles. Notação polonês é compacto e elegante, mas raro, porque é difícil para os seres humanos para lê-lo.
- Há muitas convenções diferentes sobre onde colocar parênteses; por exemplo, pode-se escrever
- Um símbolo de identidade ou igualdade = é às vezes, mas não sempre incluído no vocabulário.
- Se a igualdade é considerada como sendo uma parte da lógica de primeira ordem, em seguida, o símbolo igualdade sintacticamente se comporta como um predicado binário. Este caso é às vezes chamado de primeira ordem lógica com igualdade.
Há várias outras pequenas variações listados abaixo:
- O conjunto de símbolos primitivos (operadores e quantificadores) varia frequentemente. É possível incluir outros operadores como primitivos, como
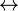 (IFF),
(IFF), 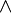 (E) e
(E) e 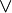 (Ou), a verdade constantes T para "true" e F para "false" (estes são operadores de valência 0), e / ou a Sheffer acidente vascular cerebral (P | Q, aka NAND). O número mínimo de símbolos primitivos necessários é um, mas se nos restringirmos aos operadores listados acima, precisamos de três, como acima.
(Ou), a verdade constantes T para "true" e F para "false" (estes são operadores de valência 0), e / ou a Sheffer acidente vascular cerebral (P | Q, aka NAND). O número mínimo de símbolos primitivos necessários é um, mas se nos restringirmos aos operadores listados acima, precisamos de três, como acima. - Alguns livros e papéis usam a notação φ
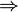 ψ para φ
ψ para φ  ψ. Isto é especialmente comum na teoria da prova, onde
ψ. Isto é especialmente comum na teoria da prova, onde  é facilmente confundido com a seta sequent. Vê-se também ~ φ para
é facilmente confundido com a seta sequent. Vê-se também ~ φ para  φ, φ e ψ para φ
φ, φ e ψ para φ 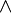 ψ, e uma riqueza de notações para quantificadores; por exemplo,
ψ, e uma riqueza de notações para quantificadores; por exemplo,  x φ pode ser escrita como (x) φ. Esta última notação é comum em textos sobre teoria da recursão.
x φ pode ser escrita como (x) φ. Esta última notação é comum em textos sobre teoria da recursão. - Muitas vezes, é mais fácil na prática de usar uma notação mais simples que suporta operadoras infixas e omite parênteses desnecessários. Assim, se P é uma relação de valência 2, que muitas vezes escrever "um P b" em vez de "P ab"; por exemplo, nós escrevemos 1 <2 em vez de <(1 2). Da mesma forma, se f é uma função da valência 2, às vezes escrever "afb" em vez de "f (ab)"; por exemplo, nós escrevemos 1 + 2 em vez de + (1 2). Por convenção, os operadores infixas tendem a usar nomes de função não-alfabéticos. Também é comum para omitir alguns parênteses se isso não leva a ambigüidade (levando a definição de uma precedência).
- Por vezes é útil para dizer que "P (x) é válida para exactamente um x", que pode ser expresso como
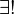 x P (x). Esta notação pode ser tomada para abreviar uma fórmula como
x P (x). Esta notação pode ser tomada para abreviar uma fórmula como 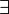 x (P (x)
x (P (x) 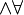 Y (P (Y)
Y (P (Y)  (X = y))).
(X = y))).
Os programas de computador que aceitam representações lógica de primeira ordem costumam aceitar pelo menos estes quantificadores e operadores (embora eles podem usar diferentes símbolos para representá-los):  (Para todos),
(Para todos), 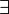 (Existe),
(Existe),  (Não),
(Não), 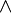 (E),
(E), 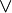 (Ou),
(Ou),  (Implica), e
(Implica), e 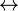 (Se e somente se). O ou-exclusivo operador "xor" também é comum.
(Se e somente se). O ou-exclusivo operador "xor" também é comum.
Os conjuntos de constantes, funções e relações são geralmente considerados para formar uma língua, enquanto as variáveis, operadores lógicos, quantificadores e são geralmente considerados como pertencendo à lógica. Por exemplo, a linguagem da teoria do grupo consiste em uma constante (o elemento de identidade), uma função de valência 1 (o inverso) uma função de valência 2 (do produto), e uma relação de valência 2 (igualdade), que seria omitido por autores que incluem a igualdade na lógica subjacente.
Regras de formação
As regras de formação de definir os termos e fórmulas da lógica de primeira ordem. Quando os termos e as fórmulas são representados como cadeias de símbolos, essas regras podem ser usadas para escrever um gramática formal para os termos e fórmulas. O conceito de variável livre é utilizado para definir as frases como um subconjunto das fórmulas.
Condições
O conjunto de termos de forma recursiva é definido pelas seguintes regras:
- Qualquer constante é um termo.
- Qualquer variável é um termo.
- Qualquer expressão f (t 1, ..., t n) de N ≥ 1 argumentos (onde cada argumento i t é um termo e f é um símbolo de função de valência n) é um termo.
- Cláusula de Encerramento: Nada mais é um termo. Por exemplo, predicados não são termos.
Fórmulas
O conjunto de fórmulas bem formadas (geralmente chamado s WFF ou apenas fórmulas) é recursivamente definido pelas seguintes regras:
- Predicados simples e complexos Se P é uma relação de valência n ≥ 1 e um i são termos então P (a 1, ..., a n) é bem-formado. Se a igualdade é considerado parte da lógica, então (a 1 = a 2) é bem formada. Todas estas fórmulas são referidos como sendo atômica.
- Cláusula indutivo I: Se φ é uma fbf, então
 φ é um wff.
φ é um wff. - Cláusula indutivo II: Se φ e ψ são s WFF, em seguida, (φ
 ψ) é uma fbf.
ψ) é uma fbf. - Cláusula indutivo III: Se φ é uma fbf e x é uma variável, então
 x φ é um wff.
x φ é um wff. - Encerramento Cláusula: Nada mais é um wff.
Por exemplo,  x
x  Y (P (f (x))
Y (P (f (x)) 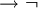 (P (x)
(P (x)  Q (f (y), x, z))) é uma fórmula bem formada, se f é uma função da valência 1, P um predicado de valência 1 e Q um predicado de valência 3.
Q (f (y), x, z))) é uma fórmula bem formada, se f é uma função da valência 1, P um predicado de valência 1 e Q um predicado de valência 3.  xx
xx  não é uma fórmula bem formada.
não é uma fórmula bem formada.
Em Informática terminologia, uma fórmula implementa um tipo de "boolean" built-in, enquanto um termo implementa todos os outros tipos.
Variáveis livres e ligadas
- Fórmulas atômicas Se φ é uma fórmula atômica então X é livre em φ se e somente se x ocorre em φ.
- Cláusula indutivo I: x é gratuito em
 φ se e somente se x é livre em φ.
φ se e somente se x é livre em φ. - Cláusula indutivo II: X é livre em (φ
 ψ) se e somente se x é livre em φ e não ocorre em ψ, ou x é gratuito em ψ e não ocorre em φ, ou x é livre em ambos φ e ψ.
ψ) se e somente se x é livre em φ e não ocorre em ψ, ou x é gratuito em ψ e não ocorre em φ, ou x é livre em ambos φ e ψ. - Cláusula indutivo III: x é gratuito em
 y φ se e somente se x é livre em φ e x é um símbolo diferente do y.
y φ se e somente se x é livre em φ e x é um símbolo diferente do y. - Encerramento Cláusula: x é encadernado em φ se e somente se x ocorre em φ e x não é livre em φ.
- Por exemplo, em
 x
x  Y (P (x)
Y (P (x)  Q (x, f (x), z) variáveis), X e Y estão ligados, z é uma variável livre, e w é nem porque não ocorre na fórmula.
Q (x, f (x), z) variáveis), X e Y estão ligados, z é uma variável livre, e w é nem porque não ocorre na fórmula.
Exemplo
Na matemática a linguagem dos grupos abelianos ordenados tem uma constante 0, uma função unário -, uma função binária +, e uma relação binária ≤. Assim:
- 0, x, y são termos atómicos
- + (X, y), + (x + (Y, - (Z))) são termos, geralmente escrita como X + Y, X + Y - Z
- = (+ (X, y), 0), ≤ (+ (x + (Y, - (Z))), + (x, y)) são fórmulas atómicas, geralmente escrita como x + y = 0, x + y - z ≤ x + y,
- (
 x
x  y ≤ (+ (x, y), z))
y ≤ (+ (x, y), z))  (
(  x = (+ (x, y), 0)) é uma fórmula, geralmente escrito como (
x = (+ (x, y), 0)) é uma fórmula, geralmente escrito como (  x
x  y x + y ≤ z)
y x + y ≤ z)  (
(  x x + y = 0).
x x + y = 0).
Substituição
Se T é um termo φ e (x) é uma fórmula contendo possivelmente x como uma variável livre, então φ (t) é definido como sendo o resultado de substituir todas as instâncias livres por x t, desde que não variável torna-se livre de t ligado neste processo. Se alguma variável livre de t fica vinculado, em seguida, substituir t para x é primeiro necessário para mudar os nomes das variáveis ligadas de φ para algo diferente do que as variáveis livres de t.
Para ver por que essa condição é necessário, considere a fórmula φ (x) dada pela  y y x ≤ ("x é máxima"). Se t é um termo sem y como uma variável livre, então φ (t) significa apenas t é máxima. No entanto, se t é y a fórmula φ (y) é
y y x ≤ ("x é máxima"). Se t é um termo sem y como uma variável livre, então φ (t) significa apenas t é máxima. No entanto, se t é y a fórmula φ (y) é  y y ≤ y que não dizer que y é máxima. O problema é que a variável y livre de t (= y) tornou-se obrigado quando nós substituímos y para x em φ (x). Então, para formar φ (y) é preciso primeiro mudar a variável ligada y de φ para outra coisa, dizer z, de modo que φ (y) é, então,
y y ≤ y que não dizer que y é máxima. O problema é que a variável y livre de t (= y) tornou-se obrigado quando nós substituímos y para x em φ (x). Então, para formar φ (y) é preciso primeiro mudar a variável ligada y de φ para outra coisa, dizer z, de modo que φ (y) é, então,  z z ≤ y. Esquecendo-se esta condição é uma causa notória de erros.
z z ≤ y. Esquecendo-se esta condição é uma causa notória de erros.
Regras de inferência
Um regra de inferência é uma função a partir de conjuntos de fórmulas (bem formados), chamado instalações, para conjuntos de fórmulas chamados conclusões. Em sistemas dedutivos mais conhecidas, regras de inferência tomar um conjunto de fórmulas para uma única conclusão. (Note que isto é verdade mesmo no caso de mais cálculos sequent.)
Regras de inferência são utilizados para provar teoremas , que são fórmulas demonstráveis em ou membros de uma teoria. Se o instalações de uma regra de inferência são teoremas, em seguida, sua conclusão é um teorema bem. Em outras palavras, regras de inferência são usados para gerar "novas" teoremas de "antigos" - eles são teoremicidade preservação. Sistemas de teorias que geram muitas vezes são chamados cálculos subjacentes. Estes são descritos numa secção abaixo.
Uma regra de inferência importante, modus ponens, afirma que, se φ e φ  ψ são ambas teoremas, então ψ é um teorema. Isto pode ser escrito como se segue;
ψ são ambas teoremas, então ψ é um teorema. Isto pode ser escrito como se segue;
- se
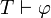 e
e 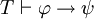 , Então
, Então 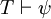
onde 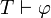 indica
indica 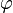 é demonstrável em teoria T. Existem sistemas dedutivos (conhecido como Hilbert-style sistemas dedutivos), no qual modus ponens é a única regra de inferência; em tais sistemas, a falta de outras regras de inferência é compensado com uma abundância de esquemas de axiomas lógicos.
é demonstrável em teoria T. Existem sistemas dedutivos (conhecido como Hilbert-style sistemas dedutivos), no qual modus ponens é a única regra de inferência; em tais sistemas, a falta de outras regras de inferência é compensado com uma abundância de esquemas de axiomas lógicos.
A segunda regra de inferência é importante Generalização Universal. Pode-se indicar como
- se
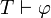 , Então
, Então 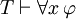
Que diz: se φ é um teorema, em seguida, "para cada x, φ" é um teorema bem. O esquema de aparência semelhante 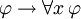 não é boa, em geral, embora não no entanto, ter instâncias válidas, como quando x não ocorre livre em φ (veja Generalização (lógica)).
não é boa, em geral, embora não no entanto, ter instâncias válidas, como quando x não ocorre livre em φ (veja Generalização (lógica)).
Axiomas
Aqui segue uma descrição dos axiomas da lógica de primeira ordem. Como explicado acima, uma determinada teoria de primeira ordem tem mais, axiomas não-lógicos. Os seguintes axiomas lógicos caracterizar um cálculo de predicados por exemplo deste artigo da lógica de primeira ordem.
Para qualquer teoria, é de interesse para saber se o conjunto de axiomas pode ser gerado por um algoritmo, ou se existe um algoritmo que determina se uma fórmula bem formada é um axioma.
Se existe um algoritmo para gerar todos os axiomas, em seguida, o conjunto de axiomas é dito ser recursivamente enumeráveis.
Se existe um algoritmo que determina depois de um número finito de passos se uma fórmula é um axioma ou não, então o conjunto de axiomas é dito ser recursivo ou decidível. Nesse caso, pode-se também construir um algoritmo para gerar todos os axiomas: Este algoritmo baseia-se simplesmente todas as fórmulas possíveis um por um (com um comprimento cada vez maior) e, para cada fórmula o algoritmo determina se é um axioma.
Axiomas da lógica de primeira ordem são sempre decidível. No entanto, numa teoria de primeira ordem axiomas não-lógicos não são necessariamente tal.
Axiomas quantificadores
Axiomas quantificadores mudar de acordo com a forma como o vocabulário é definido, como funciona o procedimento de substituição, quais são as regras de formação e que regras de inferência são utilizados. Aqui a seguir um exemplo específico destes axiomas
- PRED-1:
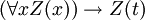
- PRED-2:
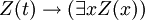
- PRED-3:
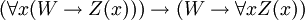
- PRED-4:
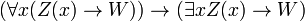
Estes são realmente axioma esquemas: a expressão W representa qualquer wff em que x não é livre, ea expressão Z (x) representa qualquer wff com a convenção adicional que Z (t) representa o resultado da substituição do termo t para x em Z (x). Assim, este é um conjunto recursivo de axiomas.
Outro axioma, 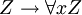 , Para Z, em que x não ocorre, é por vezes adicionada.
, Para Z, em que x não ocorre, é por vezes adicionada.
Igualdade e seus axiomas
Há várias convenções diferentes para o uso de igualdade (ou identidade) na lógica de primeira ordem. Esta seção resume os principais. As várias convenções todos dão essencialmente os mesmos resultados com aproximadamente a mesma quantidade de trabalho, e diferem principalmente na terminologia.
- A convenção mais comum para a igualdade é incluir o símbolo de igualdade como um símbolo lógico primitivo, e adicionar os axiomas para a igualdade para os axiomas para a lógica de primeira ordem. Os axiomas de igualdade são
- x = x
- x = y → f (..., x, ...) = f (..., y, ...) para qualquer função f
- x = y → (P (..., x, ...) → P (..., y, ...)) para qualquer relação P (incluindo a própria relação de igualdade)
- Estes são, também, axioma esquemas: eles definem um algoritmo que decide se uma determinada fórmula é um axioma. Assim, este é um conjunto recursivo de axiomas.
- A próxima convenção mais comum é incluir o símbolo de igualdade como uma das relações de uma teoria, e adicionar os axiomas de igualdade com os axiomas da teoria. Na prática, isso é quase indistinguível da convenção anterior, excepto no caso incomum de teorias sem noção de igualdade. Os axiomas são os mesmos, ea única diferença é se uma chama alguns deles axiomas lógicos ou axiomas da teoria.
- Em teorias sem funções e um número finito de relações, é possível definir a igualdade em termos das relações, definindo os dois termos e s t a ser igual, se qualquer relação mantém-se inalterado, alterando s para t em qualquer argumento.
- Por exemplo, em conjunto com uma teoria relação
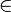 , Podemos definir s = t que é uma abreviatura para
, Podemos definir s = t que é uma abreviatura para  x (s
x (s 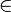 x
x 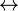 t
t 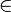 x)
x) 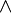
 x (x
x (x 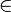 s
s 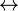 x
x 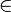 t). Esta definição de igualdade, em seguida, preenche automaticamente os axiomas de igualdade.
t). Esta definição de igualdade, em seguida, preenche automaticamente os axiomas de igualdade. - Como alternativa, se um faz usar o símbolo de igualdade como uma relação da teoria ou da lógica, então seria preciso acrescentar axiomas. No exemplo anterior, uma teria que adicionar o axioma
 s
s  t (
t (  x (x
x (x 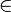 s
s 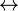 x
x 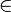 t))
t))  s = t.
s = t.
- Por exemplo, em conjunto com uma teoria relação
- Em algumas teorias é possível dar definições ad hoc de igualdade. Por exemplo, em uma teoria de pedidos parciais com uma relação ≤ podemos definir s = t que é uma abreviatura para s t ≤
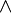 t ≤ s.
t ≤ s.
Cálculo de predicados
O cálculo de predicados é uma extensão adequada do cálculo proposicional que define quais as declarações de lógica de primeira ordem são demonstráveis. Muitos (mas não todos) teorias matemáticos podem ser formuladas no cálculo de predicados. Se o cálculo proposicional é definida com um conjunto adequado de axiomas ea única regra de inferência modus ponens (isso pode ser feito de várias maneiras), então o cálculo de predicados pode ser definida pela anexação ao cálculo proposicional vários axiomas ea regra de inferência chamado de "generalização universal". Como axiomas para o cálculo de predicados que tomamos:
- Todos os tautologias do cálculo proposicional, tomada esquematicamente de modo que a substituição uniforme de uma carta esquemática por uma fórmula é permitido.
- Os axiomas quantificadores, dado acima.
- Os axiomas acima para a igualdade, se a igualdade é considerada como um conceito lógico.
A sentença é definida para ser demonstrável na lógica de primeira ordem se ele pode ser derivada a partir dos axiomas do cálculo de predicados, aplicando repetidamente as regras de inferência "modus ponens" e "generalização universal". Em outras palavras:
- Um axioma do cálculo de predicados é demonstrável na lógica de primeira ordem, por definição.
- Se o instalações de uma regra de inferência são demonstráveis em lógica de primeira ordem, então assim também o seu conclusão.
Se temos uma teoria T (um conjunto de instruções, chamado de axiomas, em alguma língua), então uma sentença φ é definida para ser demonstrável na teoria T se
é demonstrável na lógica de primeira ordem, por algum conjunto finito de axiomas 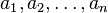 da teoria T. Em outras palavras, se se pode provar em lógica de primeira ordem que φ segue a partir dos axiomas de T. Isto significa também, que podemos substituir o procedimento acima para encontrar frases demonstráveis por a seguinte:
da teoria T. Em outras palavras, se se pode provar em lógica de primeira ordem que φ segue a partir dos axiomas de T. Isto significa também, que podemos substituir o procedimento acima para encontrar frases demonstráveis por a seguinte:
- Um axioma de T é demonstrável em T.
- Um axioma do cálculo de predicados é demonstrável em T.
- Se o instalações de uma regra de inferência são demonstráveis em T, em seguida, assim também o seu conclusão.
Um problema aparente com esta definição de provability é que parece bastante ad hoc: temos tido alguns coleção aparentemente aleatória de axiomas e regras de inferência, e não está claro que nós não perdeu acidentalmente algum axioma ou regra vital. Completude teorema de Gödel nos assegura que este não é realmente um problema: qualquer afirmação verdadeira em todos os modelos (semanticamente verdadeiros) é demonstrável na lógica de primeira ordem (sintaticamente true). Em particular, qualquer definição razoável de "provável" em lógica de primeira ordem deve ser equivalente ao de cima (embora seja possível para os comprimentos de provas para diferem substancialmente para diferentes definições de provability).
Há muitas maneiras diferentes (mas equivalentes) para definir provability. A definição acima é típico para um cálculo "estilo Hilbert", que tem muitos axiomas, mas muito poucas regras de inferência. Em contraste, uma "Estilo Gentzen" cálculo predicado tem alguns axiomas, mas muitas regras de inferência.
Identidades demonstráveis
As seguintes frases pode ser chamado de "identidades" porque o principal conectivo em cada é a bicondicional. Todos eles são demonstráveis em FOL, e são úteis ao manipular os quantificadores:
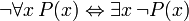
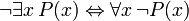
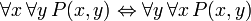
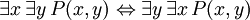
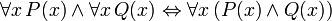
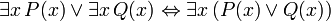
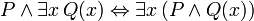 (Onde
(Onde 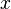 não deve ocorrer em livre
não deve ocorrer em livre 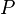 )
) 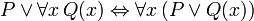 (Onde
(Onde 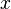 não deve ocorrer em livre
não deve ocorrer em livre 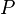 )
)
Regras de inferência demonstráveis
A principal conectivo nas seguintes frases, também demonstrável em FOL, é a condicional. Estas sentenças podem ser vistos como a justificação para regras de inferência, além de modus ponens e generalização universal discutidos acima e assumiu válido:
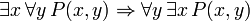
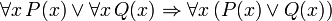
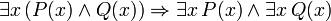
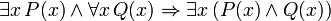
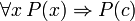 (Se c for uma variável, em seguida, ela não deve ser previamente calculados em P (x))
(Se c for uma variável, em seguida, ela não deve ser previamente calculados em P (x)) 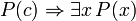 (Deve haver nenhuma instância livre de x em P (c))
(Deve haver nenhuma instância livre de x em P (c))
Teoremas metalógicos de lógica de primeira ordem
Alguns teoremas metalógicos importantes estão listados abaixo em forma de marcadores. O que eles querem dizer é que cerca de uma sentença é válido se e somente se ela é demonstrável. Além disso, pode-se construir um algoritmo que funciona da seguinte forma: se uma frase é demonstrável, o algoritmo irá nos dizer que em uma quantidade finita, mas desconhecido de tempo. Se uma sentença é improvável, o algoritmo será executado para sempre, e não vamos saber se a sentença é improvável ou provável eo algoritmo acaba ainda não nos disse isso. Tal algoritmo é chamado ou semidecidível recursivamente enumeráveis.
Pode-se construir um algoritmo que irá determinar em número finito de passos se uma sentença é demonstrável (a algoritmo decidable) apenas para as classes simples da lógica de primeira ordem.
- O problema de decisão para a validade é recursivamente enumeráveis; em outras palavras, existe uma Máquina de Turing que, quando dada qualquer sentença como entrada, irá parar se e somente se a sentença é válida (true em todos os modelos).
- Como Shows de completude teorema de Gödel, para qualquer fórmula válida P, P é demonstrável. Por outro lado, assumindo que a consistência da lógica, qualquer fórmula demonstrável é válido.
- A máquina de Turing pode ser um que gera todas as fórmulas demonstráveis da seguinte maneira: para uma ou finito recursivamente enumeráveis conjunto de axiomas, tal máquina pode ser aquele que gera um axioma, em seguida, gera uma nova fórmula demonstrável pela aplicação de axiomas e regras de inferência já gerados, em seguida, gerar um outro axioma, e assim por diante. Dada uma frase como entrada, a máquina de Turing simplesmente vá em frente e gera todas as fórmulas demonstráveis um por um, e vai parar se ele gera a sentença.
- Ao contrário do lógica proposicional, lógica de primeira ordem é indecidible, desde que a língua tem, pelo menos, um predicado de valência de pelo menos 2 do que a outra igualdade. Isto significa que não há procedimento de decisão que determina corretamente se uma fórmula arbitrária é válido. Porque existe uma máquina de Turing como descrito acima, o indecidibilidade está relacionada com a insolubilidade do Problema da parada: não existe algoritmo que determina depois de um número finito de passos se a máquina de Turing nunca vai parar por um determinado período, como sua entrada, portanto, se a sentença é demonstrável. Este resultado foi estabelecida de forma independente por Igreja e Turing .
- Lógica de predicados monádico (ou seja, a lógica de predicados com apenas predicados de um argumento e sem funções) é decidível.
- O Classe Bernays-Schönfinkel de fórmulas de primeira ordem também é decidível.
Traduzindo em linguagem natural a lógica de primeira ordem
Conceitos expressos em linguagem natural deve ser "traduzidos" para a lógica de primeira ordem (FOL) antes FOL pode ser usado para resolvê-los, e há uma série de armadilhas potenciais nesta tradução. Em FOL, 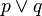 significa "p, ou Q, ou ambos", isto é, é incluído. Em Inglês, a palavra "ou" às vezes é inclusiva (por exemplo, "açúcar ou creme?"), Mas às vezes é exclusivo (por exemplo, "café ou chá?" É geralmente entendido significar um ou outro, não ambos). Da mesma forma, o Inglês palavra "alguns" pode significar "pelo menos um, possivelmente todos", mas outras vezes isso pode significar "não todos, possivelmente nenhum". A palavra Inglês "e" deve por vezes ser traduzido como "ou" (por exemplo, "homens e mulheres podem aplicar").
significa "p, ou Q, ou ambos", isto é, é incluído. Em Inglês, a palavra "ou" às vezes é inclusiva (por exemplo, "açúcar ou creme?"), Mas às vezes é exclusivo (por exemplo, "café ou chá?" É geralmente entendido significar um ou outro, não ambos). Da mesma forma, o Inglês palavra "alguns" pode significar "pelo menos um, possivelmente todos", mas outras vezes isso pode significar "não todos, possivelmente nenhum". A palavra Inglês "e" deve por vezes ser traduzido como "ou" (por exemplo, "homens e mulheres podem aplicar").
Limitações da lógica de primeira ordem
Todas as notações matemáticas têm seus pontos fortes e fracos;aqui estão algumas dessas questões com a lógica de primeira ordem.
Dificuldade representando if-then-else
Curiosamente, FOL com igualdade (como tipicamente definido) não incluir ou permitir a definição de um if-then-else predicado ou função if (c, a, b), onde "c" é uma condição expressa como uma fórmula, enquanto um e b são ou ambos os termos ou ambas as fórmulas, e seu resultado seria "a" c se é verdade, e "b" se ela é falsa. O problema é que em FOL, ambos os predicados e funções só podem aceitar os termos ("não-booleans") como parâmetros, mas a representação "óbvio" da doença é uma fórmula ("boolean"). Isso é lamentável, uma vez que muitas funções matemáticas estão convenientemente expressa em termos de if-then-else, e if-then-else é fundamental para descrever a maioria dos programas de computador.
Matematicamente, é possível redefinir um conjunto completo de novas funções que correspondem aos operadores de fórmula, mas este é bastante desajeitada. Um predicado se (c, um, b) pode ser expresso em FOL se reescrita como 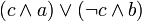 , mas este é desajeitado se a condição c é complexo. Muitos estender FOL para adicionar um predicado caso especial chamado "if (condição, a, b)" (em que a e b são fórmulas) e / ou a função "ite (condição, a, b)" (em que a e b são termos ), ambos os quais aceitam uma fórmula como a condição, e são iguais a "uma", se a condição é verdadeira e "b" se for falso. Estas extensões fazer FOL mais fácil de usar para alguns problemas, e fazer alguns tipos de-prova automática de teoremas mais fácil. Outros estendem FOL ainda mais para que as funções e predicados pode aceitar ambos os termos e fórmulas em qualquer posição.
, mas este é desajeitado se a condição c é complexo. Muitos estender FOL para adicionar um predicado caso especial chamado "if (condição, a, b)" (em que a e b são fórmulas) e / ou a função "ite (condição, a, b)" (em que a e b são termos ), ambos os quais aceitam uma fórmula como a condição, e são iguais a "uma", se a condição é verdadeira e "b" se for falso. Estas extensões fazer FOL mais fácil de usar para alguns problemas, e fazer alguns tipos de-prova automática de teoremas mais fácil. Outros estendem FOL ainda mais para que as funções e predicados pode aceitar ambos os termos e fórmulas em qualquer posição.
Typing (Sorts)
O FOL não incluem tipos (sortes) na própria notação, com excepção da diferença entre as fórmulas ("booleans") e termos ("não-booleans"). Alguns argumentam que esta falta de tipos é uma grande vantagem, mas muitos outros encontrar vantagens na definição e uso de tipos (tipos), como ajudar rejeitar algumas especificações errôneas ou indesejáveis. Aqueles que desejam indicar os tipos devem fornecer essa informação usando a notação disponível em FOL. Se o fizer, pode fazer tais expressões mais complexas, e também pode ser fácil de errar.
Predicados de parâmetro único pode ser utilizado para implementar o conceito de tipos onde apropriado. Por exemplo, em: 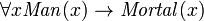 , o predicado
, o predicado 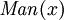 pode ser considerada como uma espécie de "tipo de afirmação" (isto é, que
pode ser considerada como uma espécie de "tipo de afirmação" (isto é, que 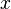 deve ser um homem). Predicados pode também ser usado com o "existe" quantificador para identificar os tipos, mas esta geralmente deve ser feito com o operador "e" em vez disso, por exemplo:
deve ser um homem). Predicados pode também ser usado com o "existe" quantificador para identificar os tipos, mas esta geralmente deve ser feito com o operador "e" em vez disso, por exemplo: 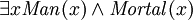 ("não existe algo que é ao mesmo tempo um homem e é mortal"). É fácil de escrever
("não existe algo que é ao mesmo tempo um homem e é mortal"). É fácil de escrever 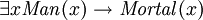 , mas isso seria equivalente a
, mas isso seria equivalente a 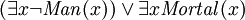 ("há algo que não é um homem, e / ou existe algo que é mortal"), que geralmente não é o que se pretendia. Da mesma forma, as afirmações podem ser feitas que um tipo é um subtipo de outro tipo, por exemplo:
("há algo que não é um homem, e / ou existe algo que é mortal"), que geralmente não é o que se pretendia. Da mesma forma, as afirmações podem ser feitas que um tipo é um subtipo de outro tipo, por exemplo: 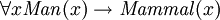 ("para todos
("para todos 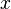 , se
, se 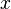 é um homem, então
é um homem, então 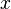 é um mamífero ").
é um mamífero ").
Dificuldade na caracterização de finitude ou responsabilização
Daqui resulta a partir da Löwenheim-Skolem teorema que não é possível caracterizar finitude ou responsabilização na lógica de primeira ordem. Por exemplo, na lógica de primeira ordem, não se pode afirmar a propriedade menos-limite superior para conjuntos de números reais , que estabelece que todo delimitada, conjunto não-vazio de números reais tem um supremo; A lógica de segunda ordem é necessário para isso.
Gráfico acessibilidade não pode ser expresso
Muitas situações podem ser modelados como um grafo de nós e as ligações dirigidas (arestas). Por exemplo, validando muitos sistemas requer que mostra que um estado "ruim" não pode ser alcançado a partir de um "bom" estado, e essas interconexões de estados muitas vezes pode ser modelado como um gráfico. No entanto, pode ser provado que conexão não pode ser totalmente expressa em lógica de predicados. Em outras palavras, não existe uma fórmula predicado-lógica 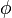 e
e 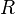 como seu único símbolo predicado (de aridade 2) tal que
como seu único símbolo predicado (de aridade 2) tal que 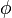 realiza em uma interpretação
realiza em uma interpretação 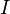 se e somente se a extensão do
se e somente se a extensão do 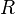 em
em 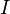 descreve um grafo conexo, ou seja, grafos conexos não pode ser axiomatizada.
descreve um grafo conexo, ou seja, grafos conexos não pode ser axiomatizada.
Note-se que dada a relação binária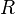 que codifica um gráfico, pode-se descrever
que codifica um gráfico, pode-se descrever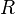 em termos de um conjunto de fórmulas de primeira ordem, e escrever uma fórmula
em termos de um conjunto de fórmulas de primeira ordem, e escrever uma fórmula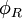 que pode ser satisfeita se e somente se
que pode ser satisfeita se e somente se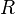 está conectado.
está conectado.
A comparação com outras lógicas
- Digitado lógica de primeira ordem permite que as variáveis e termos de ter vários tipos (ou tipos ). Se houver apenas um número finito de tipos, isso realmente não difere muito da lógica de primeira ordem, porque pode-se descrever os tipos com um número finito de predicados unários e alguns axiomas. Às vezes há uma Ω tipo especial de valores de verdade, em que as fórmulas de casos são apenas termos de tipo Ω.
- Lógica de primeira ordem com condições de domínio adiciona condições de domínio (DC) para clássico lógica de primeira ordem, permitindo a manipulação de funções parciais; estas condições pode ser comprovada "no lado" de um modo semelhante ao tipo de correção condições de PVS. Ele também adiciona if-then-else para manter definições e provas gerenciáveis (eles se tornaram demasiado complexas sem eles).
- A SMT-LIB Norma define uma linguagem utilizada por muitos grupos de pesquisa para teorias satisfiability modulo; a lógica completo é baseado em FOL com igualdade, mas acrescenta os tipos (tipos), if-then-else para os termos e fórmulas (ITE () e se .. então .. outra coisa ..), um let construir para os termos e fórmulas ( deixe e flet), e uma distinta construção declarando um conjunto de valores listados como distinta. Seus conectivos são não , implica , e , ou , xor , e sse .
- Fraco lógica de segunda ordempermite a quantificação sobre subconjuntos finitos.
- Monádica lógica de segunda ordempermite a quantificação sobre subconjuntos, ou em outras palavras maisunáriospredicados.
- Lógica de segunda ordem permite a quantificação sobre subconjuntos e relações, ou em outras palavras sobre todos os predicados. Por exemplo, a axioma da extensionalidade podem ser expressos em lógica de segunda ordem como x = y ≡ def
 P ( P ( x ) ↔ P ( y )). As fortes semântica da lógica de segunda ordem dar tais sentenças um significado muito mais forte do que semântica de primeira ordem.
P ( P ( x ) ↔ P ( y )). As fortes semântica da lógica de segunda ordem dar tais sentenças um significado muito mais forte do que semântica de primeira ordem. - Lógicas de ordem superior permite a quantificação sobre os tipos mais elevados do que de segunda ordem permite lógicas. Estes tipos superiores incluem as relações entre relações, funções de relações para as relações entre relações, etc.
- Intuitionistic lógica de primeira ordem usa intuitionistic ao invés de cálculo proposicional clássica; por exemplo, não precisa ser ¬¬φ equivalente a φ. Da mesma forma, de primeira ordem lógica difusa são extensões de primeira ordem da lógica difusa proposicional, em vez de lógica clássica.
- A lógica modaltem extrasoperadores modaiscom significados que podem ser caracterizados como informalmente, por exemplo, "é necessário que φ" e "é possível que φ".
- Em cálculo de predicados monádicopredicados são restritas a ter apenas um argumento.
- Lógica infinitary permite sentenças infinitamente longos. Por exemplo, pode-se permitir que uma conjunção ou disjunção de infinitamente muitas fórmulas, ou quantificação sobre infinitamente muitas variáveis. Infinitamente frases longas surgir nas áreas da matemática, incluindo topologia e teoria dos modelos.
- Lógica de primeira ordem com quantificadores extrastem novos quantificadoresQx, ..., com significados como "há muitosxtal que ... ". Veja também ramificação quantificadores e osquantificadores plurais deGeorge Boolos e outros.
- Lógica de Predicados com Definitions (PLD, ou D-logic) modifica FOL, acrescentando formalmente definições sintáticas como um tipo de valor (para além de fórmulas e termos); essas definições podem ser usados dentro termos e fórmulas.
- Lógica amigável-independênciaé caracterizada porquantificadores de ramificação, que permitem um para expressar independência entre variáveis quantificadas.
A maioria destas lógicas estão em algumas extensões dos sentidos de FOL: eles incluem todos os quantificadores e operadores lógicos de FOL com os mesmos significados. Lindström mostrou que FOL não tem extensões (exceto em si) que satisfaçam tanto o teorema de compacidade ea descendente teorema Löwenheim-Skolem. A indicação precisa do teorema de Lindström requer algumas condições técnicas que a lógica é assumida para satisfazer; por exemplo, alterar os símbolos de uma língua deve fazer nenhuma diferença essencial ao qual sentenças são verdadeiras.
Algebraizations
Três formas de eliminar variáveis quantificadas de FOL, e que não envolve a substituição dos quantificadores com outros operadores prazo de ligação variáveis, são conhecidos:
- Álgebra cilíndrico, porAlfred Tarski e seus colegas de trabalho;
- Álgebra poliádico, porPaul Halmos;
- Functor lógica de predicados, principalmente devido aWillard Quine.
Estasálgebras:
- São todas as extensões adequadas dodois-elemento álgebra booleana, e, portanto, sãoreticulados;
- Fazer por FOL queLindenbaum-Tarski álgebra faz porlógica sentencial;
- Aceitam os resultados deálgebra abstrata,a álgebra universal eteoria a fim de ser exercida sobre FOL.
Tarski e Givant (1987) mostram que o fragmento de FOL que não tem nenhuma sentença atômica que encontra-se no âmbito de mais de três quantificadores, tem o mesmo poder expressivo como álgebra relação. Este fragmento é de grande interesse porque é suficiente para aritmética de Peano e mais teoria dos conjuntos axiomática , incluindo o canônico ZFC. Eles também provar que FOL com um primitivo par ordenado é equivalente a uma álgebra relação com dois pares ordenados funções de projeção.
Automação
Teorema de prova para lógica de primeira ordem é um dos subcampos mais maduros de demonstração automática de teoremas. A lógica é expressivo o suficiente para permitir a especificação de problemas arbitrárias, muitas vezes de uma forma razoavelmente natural e intuitiva. Por outro lado, ainda é semidecidível, e um número de som e completos cálculos foram desenvolvidos, permitindo que os sistemas completamente automatizados. Em 1965 J. Alan Robinson conseguido um importante avanço com a sua abordagem de resolução; para provar um teorema ele tenta refutar o teorema negada, de maneira meta-dirigida, resultando em um método muito mais eficiente para provar automaticamente teoremas em FOL. Lógicas mais expressivas, como de ordem superior e lógicas modais, permitir a expressão adequada de uma gama maior de problemas do que a lógica de primeira ordem, mas teorema provando para essas lógicas é menos desenvolvida.
Uma nova tecnologia moderna e particularmente perturbador é o desolucionadores de SMT, que adicionam aritmética e apoio proposicional às classes poderosas deresolvedores SAT.