
A teoria dos jogos
Sobre este escolas selecção Wikipedia
Crianças SOS, uma instituição de caridade educação , organizou esta selecção. Uma boa maneira de ajudar outras crianças é por patrocinar uma criança
| Economia |
|---|
 Economia por país |
| Classificações gerais |
|
| Métodos técnicos |
|
| Campos e subcampos |
|
| Listas |
|
|
| A teoria dos jogos é incluído no JEL códigos de classificação: JEL: C7 |
A teoria dos jogos é um estudo da estratégica tomada de decisão. Mais formalmente, é "o estudo da modelos matemáticos de conflito e cooperação entre os decisores racionais inteligentes. "Um termo alternativo sugerido" como um nome mais descritivo para a disciplina "é interativo teoria da decisão. A teoria dos jogos é usado principalmente em economia, ciências políticas e psicologia, bem como a lógica ea biologia. O tema abordado primeiro jogos de soma zero, perdas líquidas ganhos de tal modo que uma pessoa exatamente iguais de outro participante (s). Hoje, no entanto, a teoria dos jogos se aplica a uma vasta gama de relações de classe, e tornou-se uma termo guarda-chuva para o lado lógico da ciência, para incluir ambos os seres humanos não-humanos e, como computadores. Usos clássicos incluem um senso de equilíbrio em vários jogos, onde cada pessoa tenha encontrado ou desenvolveram uma tática que não pode com sucesso melhor seus resultados, dado a outra abordagem.
Teoria dos jogos moderno começou com a idéia da existência de mixed-estratégia equilíbrios em jogos de duas pessoas de soma zero e sua prova por John von Neumann . Comprovante original de Von Neumann usado De ponto fixo teorema de Brouwer em mapeamentos contínuos em conjuntos convexos compactos, que se tornou um método padrão na teoria dos jogos e economia matemática. Seu papel foi seguido por seu livro de 1944, Teoria dos Jogos e Comportamento Econômico, com Oskar Morgenstern, que considerou jogos cooperativos de vários jogadores. A segunda edição deste livro forneceu uma teoria axiomática de utilidade esperada, o que permitiu que os estatísticos matemáticos e economistas para tratar de tomada de decisão sob incerteza.
Esta teoria foi desenvolvida extensivamente na década de 1950 por muitos estudiosos. A teoria dos jogos foi mais tarde explicitamente aplicada à biologia na década de 1970, apesar de uma evolução semelhante voltar, pelo menos tanto quanto a década de 1930. A teoria dos jogos tem sido amplamente reconhecida como uma ferramenta importante em muitos campos. Oito jogo-teóricos ganharam o Prémio de Ciências Económicas em Memória de Alfred Nobel, e John Maynard Smith foi premiado com o Prêmio Crafoord pela sua aplicação da teoria dos jogos para a biologia.
Representação de jogos
Os jogos estudados na teoria dos jogos são objetos matemáticos bem definidos. Um jogo consiste de um conjunto de jogadores, um conjunto de movimentos (ou estratégias) disponíveis para os jogadores, e uma especificação de pagamentos para cada combinação de estratégias. A maioria dos jogos cooperativos são apresentados sob a forma da função característica, enquanto que o grande e as formas normais são usados para definir os jogos não-cooperativos.
Forma extensiva

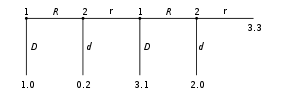
A forma extensa pode ser usado para formalizar jogos com um tempo de seqüenciamento de movimentos. Jogos aqui são jogados em árvores (como na foto à esquerda). Aqui cada vértice (ou nó) representa um ponto de escolha para um jogador. O jogador é especificado por um número indicado pelo vértice. As linhas fora do vértice representam uma possível ação para esse jogador. As recompensas são especificados na parte inferior da árvore. A forma extensiva pode ser visto como um sistema multi-jogador generalização de um árvore de decisão. (Fudenberg & Tirole 1991, p. 67)
No jogo retratado à esquerda, há dois jogadores. Jogador 1 move primeiro e escolhe F ou U. Jogador 2 vê movimento do jogador 1 's e, em seguida, escolhe uma ou R. Suponha que o Jogador 1 escolhe U e então o Jogador 2 escolhe A, então o Jogador 1 recebe 8 eo Jogador 2 obterá 2.
A forma extensiva também pode capturar jogos simultânea-movimento e jogos com informação imperfeita. Para representá-lo, seja uma linha pontilhada conecta diferentes vértices para representá-los como sendo parte do mesmo conjunto de informações (ou seja, os jogadores não sabem em que ponto eles estão), ou uma linha fechada é desenhado em torno deles. (Veja o exemplo na seção de informação imperfeita .)
Forma normal
| Jogador 2 escolhe Esquerda | Jogador 2 escolhe o botão direito | |
| Jogador 1 escolhe Up | 4, 3 | -1, -1 |
| Jogador 1 escolhe para baixo | 0, 0 | 3, 4 |
| Forma ou recompensa normal matriz de um 2-player, jogo para 2 estratégia | ||
O jogo (forma ou estratégico) normal é geralmente representado por uma matriz que mostra os jogadores, estratégias, e pagar-offs (veja o exemplo à direita). Mais geralmente, pode ser representado por qualquer função que associa um retorno para cada jogador com todas as combinações possíveis de acções. No exemplo de acompanhamento houver dois jogadores; se escolhe a linha e o outro escolhe a coluna. Cada jogador tem duas estratégias, que são especificados pelo número de linhas eo número de colunas. As recompensas são fornecidos no interior. O primeiro número é o pagamento recebido pelo jogador da linha (Jogador 1 em nosso exemplo); o segundo é a recompensa para o jogador da coluna (Jogador 2 em nosso exemplo). Suponha que um jogador joga para cima e que o jogador 2 execuções Esquerda. Em seguida, o jogador 1 recebe um retorno de 4, eo jogador recebe 2 3.
Quando um jogo é apresentado na forma normal, presume-se que cada jogador actua simultaneamente ou, pelo menos, sem conhecer as acções da outra. Se os jogadores têm alguma informação sobre as escolhas dos outros jogadores, o jogo é geralmente apresentada na forma extensiva.
Cada jogo extensa-forma tem um jogo-forma normal equivalente, no entanto, a transformação para a forma normal pode resultar em um blowup exponencial do tamanho da representação, tornando-se computacionalmente inviável. (Leyton-Brown & Shoham 2008, p. 35)
Forma função característica
Em jogos que possuem utilidade removível recompensas separadas não são dadas; em vez disso, a função característica decide a recompensa de cada unidade. A idéia é que a unidade que é "vazio", por assim dizer, não recebe uma recompensa em tudo.
A origem desta forma pode ser encontrada em John von Neumann e Oskar Morgenstern livro de; quando se olha para estes casos, eles adivinharam que, quando uma união 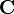 aparece, ela trabalha contra a fração
aparece, ela trabalha contra a fração 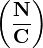 como se dois indivíduos estavam jogando um jogo normal. A recompensa equilibrada de C é uma função básica. Embora existam diferentes exemplos que ajudam a determinar quantidades de coligação de jogos normais, não aparecem todos que, na sua forma de função pode ser derivada a partir de tais.
como se dois indivíduos estavam jogando um jogo normal. A recompensa equilibrada de C é uma função básica. Embora existam diferentes exemplos que ajudam a determinar quantidades de coligação de jogos normais, não aparecem todos que, na sua forma de função pode ser derivada a partir de tais.
Formalmente, uma função característica é visto como: (N, v), em que N representa o grupo de pessoas e 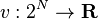 é um utilitário normal.
é um utilitário normal.
Tais funções características têm se expandido para descrever jogos onde não há nenhuma utilidade removível.
Formulário função de partição
A forma função característica ignora a possível externalidades da formação de coalizões. Na função de partição formar a recompensa de uma coalizão depende não apenas aos seus membros, mas também sobre a forma como o resto dos jogadores são divididos (Thrall & Lucas 1963).
Geral e usos aplicados
Como um método de matemática aplicada , a teoria do jogo foi utilizado para estudar uma grande variedade de comportamentos humanos e animais. Ele foi inicialmente desenvolvido na economia para entender uma grande coleção de comportamentos econômicos, incluindo comportamentos de empresas, mercados e consumidores. O uso da teoria dos jogos nas ciências sociais tem se expandido, e teoria dos jogos tem sido aplicado a comportamentos políticos, sociológicos, psicológicos e bem.
Análise de teoria dos jogos foi inicialmente utilizado para estudar o comportamento animal por Ronald Fisher na década de 1930 (embora mesmo Charles Darwin faz algumas declarações da teoria dos jogos informais). Este trabalho antecede o nome de "teoria dos jogos", mas compartilha muitas características importantes com este campo. Os desenvolvimentos na economia foram mais tarde aplicada à biologia, em grande parte por John Maynard Smith em seu livro Evolução ea Teoria dos Jogos.
Além de ser usado para descrever, prever e explicar o comportamento, a teoria dos jogos também tem sido usado para desenvolver teorias de comportamento ético ou normativa e para prescrever esse tipo de comportamento. Em economia e filosofia, estudiosos têm aplicado a teoria dos jogos para ajudar na compreensão do comportamento bom ou adequado. Argumentos da teoria dos jogos deste tipo pode ser encontrado já em Platão .
Descrição e modelação
O primeiro uso conhecido é descrever e modelo de como as populações humanas se comportam. Alguns estudiosos acreditam que encontrando os equilíbrios de jogos que pode prever como as populações humanas reais irão se comportar quando confrontados com situações análogas ao jogo que está sendo estudado. Esta visão particular da teoria dos jogos tem sido objecto de críticas recentes. Primeiro, ele é criticado porque as suposições feitas por teóricos dos jogos são frequentemente violados. Teoria dos jogos pode assumir jogadores sempre agem de forma a maximizar diretamente suas vitórias (o Homo modelo economicus), mas, na prática, muitas vezes diferente comportamento humano a partir deste modelo. Declarações de este fenômeno são muitas; irracionalidade, novos modelos de deliberação, ou mesmo diferentes motivos (como a de altruísmo ). Teóricos dos jogos respondem comparando suas suposições aos utilizados na física. Assim, enquanto suas suposições nem sempre segurar, eles podem tratar a teoria dos jogos como um científica razoável semelhante ideal para os modelos utilizados por físicos. No entanto, no jogo centopéia, acho que 2/3 do jogo média, eo jogo do ditador, as pessoas regularmente não jogam no equilíbrio de Nash. Estas experiências têm demonstrado que indivíduos não jogam estratégias de equilíbrio. Há um debate em curso sobre a importância dessas experiências.
Alternativamente, alguns autores afirmam que o equilíbrio de Nash não fornecem previsões para populações humanas, mas sim fornecer uma explicação para as populações que jogam no equilíbrio de Nash permanecer nesse estado. No entanto, a questão de como as populações alcançar esses pontos permanece em aberto.
Alguns teóricos do jogo se voltaram para teoria dos jogos evolucionária, a fim de resolver esses problemas. Estes modelos presumir ou nenhuma racionalidade ou racionalidade limitada por parte dos jogadores. Apesar do nome, a teoria dos jogos evolucionária não pressupõe necessariamente a seleção natural no sentido biológico. Teoria dos jogos evolucionária inclui tanto modelos biológicos, bem como a evolução cultural e também de aprendizagem individual (por exemplo, dinâmica de jogo fictícios).
Análise prescritiva ou normativa
| Cooperar | Defeito | |
| Cooperar | -1, -1 | -10, 0 |
| Defeito | 0, -10 | -5, -5 |
| O Dilema do Prisioneiro | ||
Por outro lado, alguns estudiosos vêem a teoria dos jogos não como uma ferramenta de previsão para o comportamento dos seres humanos, mas como uma sugestão de como as pessoas devem se comportar. Uma vez que uma estratégia, que corresponde a um equilíbrio de Nash de um jogo constitui uma de melhor resposta às ações dos outros jogadores - desde que estejam em (o mesmo) equilíbrio de Nash -, jogando uma estratégia que faz parte de um equilíbrio de Nash parece apropriado. No entanto, a racionalidade de tal decisão tenha sido provado apenas para casos especiais. Este uso normativo da teoria dos jogos também foi alvo de críticas. Em primeiro lugar, em alguns casos, é adequado para utilizar uma estratégia de não equilíbrio se espera que os outros jogar estratégias de não-equilíbrio, bem. Para um exemplo, ver acho que 2/3 da média.
Em segundo lugar, o dilema do prisioneiro apresenta outro contra-exemplo potencial. No dilema do prisioneiro, cada jogador que exerça a sua própria auto-interesse leva ambos os jogadores a ser pior do que se não tivessem prosseguido os seus próprios interesses.
Economia e negócios
A teoria dos jogos é um importante método utilizado no economia matemática e das empresas para modelar comportamentos concorrentes de interagir agentes. As aplicações incluem uma grande variedade de fenômenos e abordagens econômicas, tais como leilões, negociação, fusões e aquisições de preços, divisão justa, duopólios, oligopólios, formação de rede social, Economia computacionais baseados em agentes, equilíbrio geral, mecanismo de design, e sistemas de votação, e através de tais áreas amplas como economia experimental, a economia comportamental , economia da informação, organização industrial e economia política .
Esta pesquisa se concentra normalmente em conjuntos específicos de estratégias conhecidas como equilíbrios nos jogos. Estes "conceitos de solução" são geralmente baseados em o que é exigido pelas normas de racionalidade. Em jogos não-cooperativos, o mais famoso deles é o equilíbrio de Nash . Um conjunto de estratégias é um equilíbrio de Nash se cada um representa um melhor resposta para as outras estratégias. Então, se todos os jogadores estão jogando as estratégias em um equilíbrio de Nash, eles não têm qualquer incentivo para desviar unilateral, uma vez que sua estratégia é o melhor que podem fazer dado que os outros estão fazendo.
Os retornos do jogo são geralmente tomadas para representar a utilitário de jogadores individuais. Muitas vezes, em situações de modelagem os pagamentos representam dinheiro, o que presumivelmente corresponde a utilidade de um indivíduo. Esta hipótese, no entanto, pode estar com defeito.
Um papel prototípico na teoria dos jogos em economia começa por apresentar um jogo que é uma abstração de uma situação económica particular. Um ou mais conceitos de solução são escolhidas, eo autor demonstra que conjuntos de estratégia no jogo apresentado são equilíbrios do tipo adequado. Naturalmente pode-se perguntar para que serve esta informação deve ser colocada. Os economistas e professores de negócios sugerem dois usos primários (mencionado acima): descritiva e prescritiva.
Ciência Política
A aplicação da teoria dos jogos a ciência política está focada nas áreas de sobreposição de divisão justa, economia política , escolha pública, barganha guerra, teoria política positiva, e teoria da escolha social. Em cada uma dessas áreas, os pesquisadores desenvolveram modelos de teoria dos jogos em que os jogadores muitas vezes são os eleitores, estados, grupos de interesses especiais, e os políticos.
Para os primeiros exemplos da teoria dos jogos aplicada à ciência política, ver o trabalho de Anthony Downs. Em seu livro Uma Teoria Económica da Democracia (Downs 1957), ele aplica o Hotelling modelo local firme para o processo político. No modelo Downsian, candidatos políticos comprometem-se a ideologias em um espaço político unidimensional. Downs primeiro mostra como os candidatos políticos irão convergir para a ideologia preferida pelo eleitor mediano se os eleitores sejam plenamente informados, mas, em seguida, argumenta que os eleitores escolhem permanecer racionalmente ignorantes que permite o candidato divergência.
A explicação de teoria dos jogos para paz democrática é que o debate público e aberto nas democracias envia informação clara e fiável sobre as suas intenções para outros estados. Em contraste, é difícil saber as intenções de líderes não democráticos, que efeito terá concessões e se as promessas serão mantidos. Assim, haverá desconfiança e falta de vontade de fazer concessões se pelo menos uma das partes em litígio é uma não-democracia (Levy & Razin 2003).
Biologia
| Falcão | Pomba | |
| Falcão | 20, 20 | 80, 40 |
| Pomba | 40, 80 | 60, 60 |
| O jogo falcão-pomba | ||
Os pagamentos para jogos na biologia , ao contrário daqueles em economia, são muitas vezes interpretada como correspondendo a ginástica. Além disso, o foco tem sido menos sobre equilíbrios que correspondem a uma noção de racionalidade e muito mais no os que seriam mantidos pelo evolutivas forças. O equilíbrio mais conhecido na biologia é conhecida como a estratégia evolutivamente estável (ou ESS), e foi introduzido pela primeira vez em (Smith & Price, 1973). Embora sua motivação inicial não envolveu qualquer um dos requisitos mentais do equilíbrio de Nash , cada ESS é um equilíbrio de Nash.
Em biologia, a teoria dos jogos foi usada para compreender muitos fenômenos diferentes. Foi usado pela primeira vez para explicar a evolução (e estabilidade) do aproximada de 1: 1 relações sexuais. (Fisher 1930) sugeriu que o 1: 1 proporções de sexo são o resultado de forças evolutivas que atuam sobre os indivíduos que poderia ser visto como uma tentativa de maximizar o seu número de netos.
Além disso, os biólogos têm usado teoria dos jogos evolucionária eo SEE para explicar o surgimento de comunicação animal (Harper & Maynard Smith, 2003). A análise de jogos de sinalização e outros jogos de comunicação tem proporcionado uma visão sobre a evolução da comunicação entre animais. Por exemplo, a mobbing comportamento de muitos espécies, em que um grande número de presas atacam um grande predador, parece ser um exemplo de organização espontânea emergente. Formigas também foram mostrados para apresentar um comportamento forward-alimentação semelhante a moda, consulte Economia borboleta.
Os biólogos têm usado o jogo da galinha para analisar o comportamento de luta e territorialidade.
Maynard Smith, no prefácio de Evolução ea Teoria dos Jogos, escreve, "paradoxalmente, tem-se que a teoria dos jogos é mais facilmente aplicada a biologia do que ao campo do comportamento económico para a qual foi originalmente concebido". Teoria dos jogos evolucionária tem sido usada para explicar muitos fenômenos aparentemente incongruentes na natureza.
Um tal fenômeno é conhecido como altruísmo biológico. Esta é uma situação em que um organismo parece actuar de um modo que beneficia outros organismos e é prejudicial para si. Isso é diferente de noções tradicionais de altruísmo, porque tais ações não são conscientes, mas parecem ser adaptações evolutivas para aumentar a aptidão total. Exemplos podem ser encontrados em espécies que variam de morcegos hematófagos que regurgitam sangue que tenham obtido a partir de caça de uma noite e dar-lhe aos membros do grupo que não conseguiram se alimentar, a abelhas operárias que cuidam da abelha rainha durante toda a vida e nunca se acasalam, a os macacos que advertem os membros do grupo de abordagem de um predador, mesmo quando se põe em perigo a chance de que um indivíduo de sobrevivência. Todas estas acções aumentar a aptidão geral de um grupo, mas ocorrem a um custo para o indivíduo.
Teoria dos jogos evolucionária explica esse altruísmo com a idéia de seleção de parentesco. Altruists discriminar entre as pessoas que ajudam e parentes favor. Regra de Hamilton explica o raciocínio por trás dessa seleção evolutiva com a equação c A teoria dos jogos tem vindo a desempenhar um papel cada vez mais importante na lógica e na ciência da computação . Várias teorias lógicas têm uma base na semântica de jogo. Além disso, cientistas da computação têm usado os jogos para modelar cálculos interativos. Além disso, a teoria dos jogos proporciona uma base teórica para o campo da sistemas multi-agente. Separadamente, a teoria dos jogos tem desempenhado um papel na algoritmos de linha. Em particular, o problema k-servidor, que, no passado, sido referido como jogos com os custos de móveis e jogos de solicitação-resposta (Ben David, Borodin & Karp et al., 1994). Princípio de Yao é uma técnica de teoria dos jogos para provar limites inferiores na complexidade computacional randomizados algoritmos, e especialmente em linha de algoritmos. O surgimento da internet tem motivado o desenvolvimento de algoritmos para encontrar equilíbrios em jogos, mercados, leilões computacionais, sistemas peer-to-peer, e os mercados de segurança e de informação. Teoria dos jogos algorítmica e dentro dele algorítmica projeto mecanismo combinar computacional algoritmo de projeto e análise de sistemas complexos com a teoria econômica. A teoria dos jogos tem sido objecto de várias utilizações em filosofia . Respondendo a dois artigos por WVO Quine (1960, 1967), Lewis (1969) usou a teoria dos jogos para desenvolver uma explicação filosófica de convenção. Ao fazê-lo, ele forneceu a primeira análise de conhecimento comum e empregou-o na análise de jogo em jogos de coordenação. Além disso, ele sugeriu primeiro que se pode compreender o que significa, em termos de sinalização jogos. Esta sugestão mais tarde foi perseguido por vários filósofos desde Lewis (Skyrms (1996), Grim, Kokalis, e Alai-Tafti et al. (2004)). Seguindo Lewis (1969) conta de teoria dos jogos de convenções, Edna Ullmann-Margalit (1977) e Bicchieri (2006) desenvolveram teorias de normas sociais que os definem como equilíbrio de Nash que resultam da transformação de um jogo misto motivo em um jogo de coordenação. A teoria dos jogos também tem desafiado filósofos a pensar em termos de interativo epistemologia: o que significa para um coletivo de ter crenças ou conhecimento comum, e quais são as conseqüências desse conhecimento para os resultados sociais resultantes da interação dos agentes. Os filósofos que trabalharam nesta área incluem Bicchieri (1989, 1993), Skyrms (1990), e Stalnaker (1999). Na ética , alguns autores tentaram prosseguir o projecto, iniciado por Thomas Hobbes , de derivar a moralidade do auto-interesse. Desde jogos como o dilema do prisioneiro apresenta um aparente conflito entre a moralidade eo interesse próprio, explicando porque a cooperação é necessária pelo auto-interesse é um componente importante deste projecto. Esta estratégia geral é um componente do geral visão contrato social em filosofia política (para exemplos, ver Gauthier (1986) e Kavka (1986). Outros autores têm tentado usar teoria dos jogos evolucionária para explicar o surgimento de atitudes humanas sobre a moralidade e comportamentos animais correspondentes. Estes autores olhar para vários jogos, incluindo o dilema do prisioneiro, caça ao veado, eo Jogo de barganha de Nash como fornecendo uma explicação para o surgimento de atitudes sobre a moralidade (ver, por exemplo, Skyrms (1996, 2004) e Sober e Wilson (1999)). Algumas premissas utilizadas em algumas partes da teoria dos jogos têm sido desafiados em filosofia; por exemplo, egoísmo psicológico afirma que a racionalidade reduz a auto-interesse uma reivindicação debatido entre os filósofos. (Veja Egoísmo psicológico # críticas) Um jogo é cooperativo se os jogadores são capazes de formar compromissos vinculativos. Por exemplo, o sistema jurídico obriga-os a aderir a suas promessas. Em jogos não-cooperativos isto não é possível. Muitas vezes, presume-se que a comunicação entre os jogadores é permitido em jogos cooperativos, mas não nos não-cooperativos. No entanto, esta classificação em dois critérios binários tem sido questionada, e às vezes rejeitados (Harsanyi 1974). Dos dois tipos de jogos, jogos não-cooperativos são capazes de modelar situações para os detalhes mais finos, produzindo resultados precisos. Jogos cooperativos se concentrar no jogo em geral. Foram envidados esforços consideráveis para ligar as duas abordagens. O chamado programa-Nash já estabeleceu muitas das soluções de cooperação como equilíbrios não-cooperativos. Jogos híbridos contêm elementos cooperativos e não cooperativos. Por exemplo, os conselhos de jogadores são formados numa jogo cooperativo, mas estes desempenham de forma não-cooperativo. Um jogo simétrico é um jogo onde os retornos para a reprodução de uma determinada estratégia depende apenas dos outros estratégias empregadas, não de quem está jogando. Se a identidade dos jogadores pode ser alterado sem alterar a recompensa para as estratégias, em seguida, um jogo é simétrica. Muitos dos comumente estudados 2 × 2 jogos são simétricas. As representações padrão de frango, o dilema do prisioneiro, eo caça ao veado são todos jogos simétricos. Alguns estudiosos consideram certos jogos assimétricos como exemplos desses jogos também. No entanto, os pagamentos mais comuns para cada um destes jogos são simétricas. Mais comumente jogos assimétricos estudados são os jogos onde não existem conjuntos de estratégia idênticas para ambos os jogadores. Por exemplo, o jogo ultimato e da mesma forma o jogo do ditador tem estratégias diferentes para cada jogador. É possível, no entanto, para um jogo ter estratégias idênticas para ambos os jogadores, ainda ser assimétrica. Por exemplo, o jogo ilustrado à direita é assimétrica, apesar de ter conjuntos de estratégia idênticas para ambos os jogadores. Jogos de soma zero são um caso especial de jogos de soma constante, em que as escolhas por jogadores não podem aumentar nem diminuir os recursos disponíveis. Em jogos de soma zero, o benefício total para todos os jogadores no jogo, para cada combinação de estratégias, sempre somam zero (mais informalmente, benefícios Um jogador só à custa igual de outros). Pôquer exemplifica um jogo de soma zero (ignorando a possibilidade de corte da casa), porque se ganha exatamente a quantidade de um adversário perder. Outros jogos de soma zero incluem moedas de um centavo ea maioria dos jogos de tabuleiro clássicos, incluindo correspondentes Go e xadrez . Muitos jogos estudados pelos teóricos dos jogos (incluindo o infame dilema do prisioneiro) são jogos de soma zero, porque o resultado tem resultado líquido maior ou menor que zero. Informalmente, em jogos de soma zero, um ganho por um jogador não corresponde necessariamente a uma perda por outro. Jogos de soma constante correspondem a atividades como roubo e jogos de azar, mas não para a situação económica fundamental em que há potencial ganhos do comércio. É possível transformar qualquer jogo em um (possivelmente assimétrico) jogo de soma zero pela adição de um jogador fictício adicional (muitas vezes chamado de "o conselho"), cujas perdas compensar ganhos líquidos dos jogadores. Jogos simultâneos são jogos onde ambos os jogadores se movem simultaneamente, ou se eles não se movem ao mesmo tempo, os jogadores posteriores não têm conhecimento das ações dos jogadores anteriores (tornando-os efectivamente simultâneos). Jogos sequenciais (ou jogos dinâmicos) são jogos onde os jogadores posteriores têm algum conhecimento sobre as ações anteriores. Isto não é necessariamente informação perfeita sobre cada ação dos jogadores mais antigos; que poderia ser muito pouco conhecimento. Por exemplo, um jogador pode saber que um jogador anteriormente não executar uma determinada ação, enquanto ele não sabe quais das outras ações disponíveis o primeiro jogador realmente executada. A diferença entre jogos simultâneos e sequenciais é capturada nas diferentes representações discutidas acima. Muitas vezes, forma normal é usada para representar jogos simultâneos, e forma extensiva é usada para representar os seqüenciais. A transformação da forma normal para grande é uma forma, o que significa que vários jogos de forma extensa correspondem à mesma forma normal. Por conseguinte, as noções de equilíbrio para jogos simultâneos são insuficientes para raciocinar sobre jogos sequenciais; ver subgame perfeição. Em suma, as diferenças entre sequencial e jogos simultâneas são os seguintes: Um subconjunto de jogos sequenciais importante consiste em jogos de informação perfeita. Um jogo é um dos informação perfeita se todos os jogadores conhecem os movimentos prévios feitos por todos os outros jogadores. Assim, somente jogos seqüenciais podem ser jogos de informação perfeita porque os jogadores em jogos simultâneos não sei as ações dos outros jogadores. A maioria dos jogos estudados na teoria dos jogos são jogos de informação imperfeita. Exemplos interessantes de jogos perfeito-de informação incluem o jogo do ultimato e jogo centopéia. Jogos recreativos de jogos de informação perfeita incluem xadrez , go e mancala . Muitos jogos de cartas são jogos de informação imperfeita, por exemplo poker ou ponte de contrato. Informação perfeita é freqüentemente confundida com informação completa, que é um conceito semelhante. Informação completa requer que cada jogador sabe as estratégias e pagamentos disponíveis para os outros jogadores, mas não necessariamente as ações tomadas. Jogos de informação incompleta pode ser reduzida, no entanto, para jogos de informação imperfeita, introduzindo " movimentos por natureza "(Leyton-Brown & Shoham 2008, p. 60). Jogos em que a dificuldade de encontrar uma estratégia ótima hastes da multiplicidade de movimentos possíveis são chamados jogos combinatórios. Exemplos incluem xadrez e ir embora. Jogos que envolvem informação imperfeita ou incompleta também pode ter um caráter forte combinatória, por exemplo gamão . Não existe uma teoria unificada abordando elementos combinatórios em jogos. Há, no entanto, ferramentas matemáticas que podem resolver problemas particulares e responder a perguntas gerais. Jogos de informação perfeita foram estudadas em teoria de jogos combinatórios, que desenvolveu novas representações, por exemplo, números surreais, bem como combinatória e algébrico (e às vezes não-construtivas) métodos de prova para resolver jogos de determinados tipos, incluindo jogos "loopy" que podem resultar em infinitamente longas sequências de movimentos. Estes métodos resolver jogos com complexidade combinatória superiores aos montantes normalmente considerado na teoria dos jogos tradicional (ou "econômico"). Um jogo típico que foi resolvido dessa forma é hex. Uma áreas afins de estudo, desenho de teoria da complexidade computacional, é complexidade jogo, que está preocupado com a estimativa da dificuldade computacional de encontrar estratégias ótimas. Pesquisa em inteligência artificial abordou os dois jogos perfeitos e imperfeitos (ou incompletos) de informação que têm estruturas combinatórias muito complexos (como o xadrez, go, ou gamão) para os quais não foram encontradas estratégias ótimas comprováveis. As soluções práticas envolvem heurística computacional, como alfa-beta a poda ou o uso de redes neurais artificiais formados por aprendizado por reforço, o que torna os jogos mais dócil na prática de computação. Jogos, como estudado por economistas e jogadores do mundo real, geralmente terminam em um número finito de movimentos. Matemáticos puros não estão tão constrangidos, e definir os teóricos em particular estudam jogos que duram infinitamente muitos movimentos, com o vencedor (ou outra recompensa) não conhecidos até após todos estes movimentos tenham sido completados. O foco da atenção é usualmente não tanto sobre o que é a melhor maneira de jogar tal jogo, mas simplesmente sobre se um ou outro jogador tem uma estratégia vencedora. (Ele pode ser comprovada, usando o axioma da escolha, que há jogos, mesmo com informação perfeita, e onde os únicos resultados são "ganhar" ou "perder" para o qual nenhum jogador tem uma estratégia vencedora.) A existência de tais estratégias, para jogos inteligentemente concebido, tem consequências importantes teoria descritiva dos conjuntos. Grande parte da teoria dos jogos está preocupado com, jogos discretos finitos, que tem um número finito de jogadores, movimentos, eventos, resultados, etc. Muitos conceitos podem ser estendidos, no entanto. Jogos contínuos permitem que os jogadores para escolher uma estratégia de um jogo de estratégia contínua. Por exemplo, Competição de Cournot é tipicamente modelados com as estratégias dos jogadores sendo as quantidades não-negativas, incluindo as quantidades fracionadas. Jogos diferenciais, como o contínuo perseguição e jogo de evasão são os jogos contínuos, onde a evolução das variáveis de estado dos jogadores é regido por equações diferenciais . O problema de encontrar uma melhor estratégia em um jogo diferencial está intimamente relacionado com o teoria do controle ótimo. Em particular, existem dois tipos de estratégias: as estratégias de malha aberta são encontradas usando o Pontryagin princípio máximo enquanto as estratégias de circuito fechado são encontrados usando Método de programação dinâmica de Bellman. Um caso particular de jogos diferenciais são os jogos com horizonte de tempo aleatório. Nestes jogos, o terminal de tempo é uma variável aleatória com uma determinada distribuição de probabilidade função. Por isso, os jogadores a maximizar expectativa matemática da função de custo. Foi demonstrado que o problema de optimização modificado pode ser reformulado como um jogo diferencial descontadas ao longo de um intervalo de tempo infinito. Jogos com um arbitrário, mas finito, número de jogadores são freqüentemente chamados de n-pessoa jogos (Luce & Raiffa 1957). Teoria dos jogos evolucionária considera jogos envolvendo um população de tomadores de decisão, onde a frequência com que é feita a uma determinada decisão pode mudar ao longo do tempo em resposta às decisões tomadas por todos os indivíduos da população. Em biologia, este destina-se a modelar (biológico) evolução , onde organismos geneticamente programados passar ao longo de alguns dos seus programas estratégia para sua prole.Na economia, a mesma teoria se destina a captar mudanças da população, porque as pessoas jogar o jogo muitas vezes dentro de sua vida, e conscientemente (e talvez racionalmente) as estratégias de comutação (Webb, 2007). Problemas de decisão individuais com resultados estocásticos são considerados às vezes "jogos de um jogador". Estas situações não são consideradas jogo teórica por alguns autores. Eles podem ser modeladas utilizando ferramentas semelhantes dentro das disciplinas relacionadas de teoria da decisão, pesquisa de operações e áreas de inteligência artificial, particularmente AI planejamento (com incerteza) e sistema multi-agente. Embora esses campos podem ter diferentes motivações, a matemática envolvidos são substancialmente o mesmo, por exemplo, usando processos de decisão de Markov (MDP). Resultados estocásticos também pode ser modelado em termos de teoria dos jogos, adicionando um jogador agir de forma aleatória que faz "movimentos chance", também conhecidos como " movimentos por natureza "(Osborne e Rubinstein, 1994). Este jogador não é normalmente considerada um terceiro jogador no que é o contrário de um jogo para dois jogadores, mas serve apenas para fornecer um rolo dos dados, quando necessário pelo jogo. Para alguns problemas, diferentes abordagens para resultados de modelagem estocástica pode conduzir a soluções diferentes. Por exemplo, a diferença de abordagem entre MDPs ea solução minimax é que este último considera o pior caso sobre um conjunto de movimentos contraditórios, ao invés de raciocínio na expectativa sobre estes movimentos dado uma distribuição de probabilidade fixa. A abordagem minimax pode ser vantajosa onde os modelos estocásticos de incerteza não estão disponíveis, mas também pode estar superestimando os eventos extremamente improváveis (mas caros), oscilando drasticamente a estratégia em tais cenários que se admita que um adversário pode forçar um evento como esse acontecer. (Ver teoria cisne negro para mais discussão sobre este tipo de problema de modelagem, particularmente no que se refere à previsão e limitar as perdas na banca de investimento.) Modelos gerais que incluem todos os elementos de resultados estocásticos, adversários, e observabilidade parcial ou barulhento (de movimentos por outros jogadores) também foram estudadas. O " padrão ouro "é considerada parcialmente observável jogo estocástico (POSG), mas alguns problemas realistas são computacionalmente viável em representação POSG. Estes são os jogos a jogar do que é o desenvolvimento das regras para outro jogo, o alvo ou sujeitas jogo. Metagames procuram maximizar o valor de utilidade do conjunto de regras desenvolvido. A teoria da metagames está relacionada com a teoria do desenho de mecanismos. O termo análise metagame também é usado para se referir a uma abordagem prática desenvolvida por Nigel Howard (Howard 1971) em que uma situação é enquadrado como um jogo estratégico em que as partes interessadas tentar realizar seus objetivos por meio das opções disponíveis para eles. Desenvolvimentos posteriores levaram à formulação de análise confronto. Primeiras discussões de exemplos de jogos de duas pessoas ocorreu muito antes do surgimento da teoria dos jogos modernos, matemático. A primeira discussão conhecida da teoria dos jogos ocorreu em uma carta escrita por James Waldegrave em 1713. Nesta carta, Waldegrave fornece um minimax solução de estratégia mista para uma versão de duas pessoas do jogo de cartas le Her. James Madison fez o que hoje reconhecemos como uma análise da teoria dos jogos das maneiras estados pode ser esperado para se comportar em diferentes sistemas de tributação. Em seu 1838 Recherches sur les principes mathématiques de la théorie des richesses ( pesquisas sobre os Princípios Matemáticos da Teoria da Riqueza ), Antoine Augustin Cournot considerado um duopólio e apresenta uma solução que é uma versão restrita do equilíbrio de Nash . O matemático dinamarquês Zeuthen provado que o modelo matemático tinha uma estratégia vencedora, usando teorema de ponto fixo de Brouwer. Em seus 1938 livro Applications aux Jeux de Hasard e notas anteriores, Émile Borel provou um teorema minimax para duas pessoas de soma zero jogos de matriz somente quando a matriz pay-off era simétrico. Borel conjecturou que não existência de mixed-estratégia de equilíbrio em jogos de duas pessoas de soma zero iria ocorrer, uma conjectura que se provou falsa. A teoria dos jogos realmente não existe como um campo exclusivo até que John von Neumann publicou um artigo na prova original de 1928. Von Neumann usado de ponto fixo teorema de Brouwer em mapeamentos contínuos em conjuntos convexos compactos, que se tornou um método padrão na teoria dos jogos e economia matemática. Seu papel foi seguido por seu livro de 1944, Teoria dos Jogos e Comportamento Econômico . A segunda edição deste livro forneceu uma teoria axiomática da utilidade, que reencarnou velha teoria da utilidade (do dinheiro) de Daniel Bernoulli como disciplina independente. O trabalho de Von Neumann na teoria dos jogos culminou neste livro de 1944. Este trabalho de base contém o método para encontrar soluções mutuamente coerentes para jogos de duas pessoas de soma zero. Durante o próximo período de tempo, o trabalho sobre a teoria dos jogos foi focado principalmente em teoria dos jogos cooperativos, que analisa estratégias ótimas para grupos de indivíduos, presumindo que eles possam aplicar convenções entre eles sobre as estratégias adequadas. Em 1950, a primeira discussão matemática do dilema do prisioneiro apareceu, e um experimento foi realizado por matemáticos notáveis Merrill M. Flood e Melvin Dresher, como parte da investigação da corporação RAND em teoria dos jogos. Rand prosseguido os estudos por causa de possíveis aplicações para mundial estratégia nuclear. em torno deste mesmo tempo, John Nash desenvolveu um critério de coerência entre as estratégias dos jogadores, conhecidas como equilíbrio de Nash, aplicável a uma ampla variedade de jogos do que o critério proposto por von Neumann e Morgenstern. Este equilíbrio é suficientemente geral para permitir a análise de jogos não-cooperativos para além dos cooperados. A teoria dos jogos experimentou uma onda de atividade na década de 1950, período durante o qual os conceitos do núcleo, o grande jogo de forma, jogo fictício, jogos repetidos, eo valor de Shapley foram desenvolvidos. Além disso, as primeiras aplicações da teoria dos jogos para filosofia e ciência política ocorreram durante este tempo. Em 1965, Reinhard Selten introduziu seu conceito de solução do equilíbrio perfeito sub-jogo, que refinou ainda mais o equilíbrio de Nash (mais tarde ele iria introduzir perfeição mão trêmula também). Em 1967, John Harsanyi desenvolveu os conceitos de informação completa e jogos Bayesianos. Nash, Selten e Harsanyi tornou-se Economics Nobel Laureates em 1994 por suas contribuições à teoria dos jogos econômica. Nos anos 1970, a teoria dos jogos foi amplamente aplicada em biologia , em grande parte como resultado do trabalho de John Maynard Smith e sua estratégia evolutivamente estável . Além disso, os conceitos de equilíbrio correlacionado, perfeição mão trêmula, e conhecimento comum foram introduzidos e analisados. Em 2005, os teóricos dos jogos Thomas Schelling e Robert Aumann seguido Nash, Selten e Harsanyi como ganhadores do Prêmio Nobel. Schelling trabalhou no modelos dinâmicos, os primeiros exemplos de teoria dos jogos evolucionária. Aumann contribuiu mais para a escola de equilíbrio, a introdução de um engrossamento de equilíbrio, equilíbrio correlacionado, e desenvolvendo uma extensa análise formal da assunção de conhecimento comum e de suas conseqüências. Em 2007, Leonid Hurwicz, juntamente com Eric Maskin e Roger Myerson, foi agraciado com o Prêmio Nobel de Economia "por ter lançou as bases da teoria do desenho de mecanismos ". As contribuições de Myerson incluir a noção de equilíbrio adequado, e um importante texto de pós-graduação: Teoria dos Jogos, Análise de Conflitos (Myerson 1997). Hurwicz introduziu e formalizou o conceito de compatibilidade de incentivos. A história de vida do jogo teórico e matemáticoJohn Nash foi transformado em um filme biográfico, Uma Mente Brilhante, estrelado porRussell Crowe, baseado no livro deSylvia Nasar. "Jogos-teoria" e "teoria dos jogos" são mencionados no romance de ficção científica militar Starship Troopers por Robert A. Heinlein. No filme de mesmo nome de 1997, o personagem Carl Jenkins se refere à sua atribuição, inteligência militar, como "jogos e teoria." Uma das principais gameplay de decisão mecânica do jogo de vídeo Zero fuga: da Virtude Última recompensa é baseada na teoria dos jogos. Alguns dos personagens ainda referenciar o dilema do prisioneiro. O filme Dr. Strangelove satiriza jogo idéias teóricas sobre teoria da dissuasão. Por exemplo, a dissuasão nuclear depende da ameaça de retaliar catastroficamente se um ataque nuclear é detectado. Um teórico jogo pode-se argumentar que tais ameaças podem deixar de ser credível , no sentido de que eles podem levar a sub-jogo equilíbrios imperfeitos. O filme leva essa idéia um passo adiante, com os russos irrevogavelmente se comprometer com uma resposta nuclear catastrófico sem fazer o público ameaça. Ciência da computação e lógica
Filosofia
Especulador Lebre
Especulador 3, 3 0, 2 Lebre 2, 0 2, 2 Caça ao veado Tipos de jogos
Cooperativa ou não-cooperativo
Simétrica e assimétrica
E F E 1, 2 0, 0 F 0, 0 1, 2 Um jogo assimétrico Zero-soma e não de soma zero
A B A -1, 1 3, -3 B 0, 0 -2, 2 Um jogo de soma zero Simultânea e seqüencial
Seqüente Simultâneo Normalmente denotado por: Árvores de Decisão Payoff Matrizes O conhecimento prévio da jogada do adversário: Sim Não Tempo Axis: Sim Não Também conhecido como: Extensa Jogo Jogo estratégico Informação perfeita e informação imperfeita

![]()
Jogos combinatórios
Jogos infinitamente longos
Jogos discretas e contínuas
Jogos diferenciais
Muitos-player e jogos população
Resultados estocásticos (e relativamente a outros campos)
Metagames
História
Cultura popular


