
Desigualdade (matemática)
Sobre este escolas selecção Wikipedia
Crianças SOS feita esta seleção Wikipedia ao lado de outras escolas recursos . Crianças SOS é a maior doação de caridade do mundo órfãos e crianças abandonadas a chance da vida familiar.
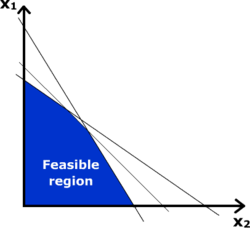
Em matemática , uma desigualdade é uma declaração sobre a dimensão relativa ou essa ordem de dois objetos. (Veja também: igualdade)
- A notação
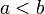 significa que um é inferior a b e
significa que um é inferior a b e - A notação
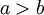 significa que a é maior do que b.
significa que a é maior do que b.
Essas relações são conhecidos como desigualdade estrita; em contraste
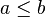 significa que a é menor do que ou igual a b;
significa que a é menor do que ou igual a b; 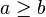 significa que a é maior que ou igual a b;
significa que a é maior que ou igual a b; 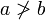 significa que um não é maior do que b e
significa que um não é maior do que b e 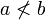 significa que um não é menos do que b.
significa que um não é menos do que b.
Um uso adicional da notação é mostrar que uma quantidade é muito maior do que outra, normalmente por várias ordens de grandeza.
- A notação
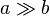 significa que um é muito maior do que b.
significa que um é muito maior do que b. - A notação
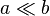 significa que um é muito menos do que b.
significa que um é muito menos do que b.
Se o sentido da desigualdade é o mesmo para todos os valores das variáveis para que os seus membros estão definidas, então a desigualdade é chamada de desigualdade "absoluta" ou "incondicional". Se o sentido de uma desigualdade detém apenas para determinados valores das variáveis envolvidas, mas é invertida ou destruídos por outros valores das variáveis, ela é chamada de desigualdade condicional. O sentido de uma desigualdade não for alterada, se ambos os lados são aumentadas ou diminuídas pela mesma quantidade, ou se ambos os lados são multiplicados ou dividido por um número positivo; no sentido de uma desigualdade é revertida se ambos os membros são multiplicados ou dividido por um número negativo .
Propriedades
As desigualdades são regidos pelas seguintes propriedades . Note-se que, para a transitividade, reversão, adição e subtração, multiplicação e divisão e propriedades, a propriedade também tem se estritas sinais de desigualdade (<e>) são substituídos por seus correspondentes sinal não-estrita desigualdade (≤ e ≥).
Tricotomia
O estados da propriedade tricotomia:
- Para todos os números reais , a e b, exatamente uma das seguintes opções for verdadeira:
- a <b
- a = b
- a> b
Transitividade
O transitividade das desigualdades afirma:
- Para todos os números reais , a, b, c:
- Se a> b e b> c; em seguida, a> c
- Se a <b e b <c; então a <c
Reversão
As relações de desigualdade são relações inversas:
- Para qualquer números reais , a e b:
- Se a> b, em seguida, b <a
- Se a <b, então b> a
Adição e subtração
As propriedades que lidam com adição e subtração estado:
- Para todos os números reais , a, b, c:
- Se a> b, em seguida a + c> b + c e um - C> b - c
- Se a <b, então a + c <b + c e a - c <b - c
ou seja, os números reais são uma grupo encomendado.
Multiplicação e divisão
As propriedades que lidam com a multiplicação e divisão estado:
- Para todos os números reais, a, b, c:
- Se c for positivo e um <b, então ac <bc
- Se c é negativo e um <b, então ac> bc
Mais geralmente, esta aplica-se para uma campo ordenado, veja abaixo.
Inverso aditivo
As propriedades para o aditivo estado inverso:
- Para qualquer um número real e b
- Se a <b então - a> - b
- Se a> b então - a <- b
Inverso multiplicativo
As propriedades para o multiplicativo estado inverso:
- Para qualquer números a e b real que são ambos positivo ou ambos negativo
- Se a <b então um / a> 1 / b
- Se a> b então um / a <1 / b
Aplicando uma função de ambos os lados
Consideramos dois casos de funções: monótona e estritamente monótona.
Qualquer estritamente monótona crescente função pode ser aplicada a ambos os lados de uma desigualdade e ele ainda vai realizar. Aplicando uma função estritamente monotonicamente decrescente para ambos os lados de uma desigualdade significa que a desigualdade oposto agora detém. As regras para aditivos e multiplicativos inversas são exemplos de aplicação de uma função monotônica decrescente.
Se você tem uma desigualdade não estrita (a ≤ b, a ≥ b), então:
- Aplicando uma função monotônica crescente preserva a relação (≤ permanece ≤, ≥ permanece ≥)
- Aplicando uma função monotonicamente decrescente inverte a relação (≤ ≥ torna-se, torna-se ≥ ≤)
Ele nunca vai se tornar estritamente desigual, uma vez que, por exemplo, 3 ≤ 3 não implica que 3 <3.
Campos ordenados
Se F, +, * ser um ≤ campo e ser um ordem total sobre F, em seguida, F, +, *, ≤ é chamado de campo, se e somente se ordenou:
- Se um ≤ b + c, em seguida, uma ≤ b + c
- se ≤ 0 e um 0 ≤ b ≤ 0, em seguida, ab
Note-se que tanto 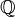 , +, *, E ≤
, +, *, E ≤ 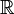 , +, *, São ≤ campos solicitados.
, +, *, São ≤ campos solicitados.
≤ não pode ser definida, a fim de fazer 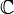 , +, *, Uma ≤ campo ordenada.
, +, *, Uma ≤ campo ordenada.
As desigualdades não-rigorosos e ≤ ≥ sobre os números reais são total de encomendas. As desigualdades estritas <e> em números reais são Módulo: Total_order ( falar · · hist · Links · subpages · testes - resultados).
Notação Acorrentado
A notação a <b <c significa "a <b e b <c", do qual, pela propriedade de transitividade acima, segue-se também que a <c. Obviamente, pelas leis acima, pode-se adicionar / subtrair o mesmo número para todos os três termos, ou multiplicar / dividir todos os três termos por mesmo número diferente de zero e reverter todas as desigualdades de acordo a assinar. . Mas é preciso ter cuidado para que você realmente usar o mesmo número em todos os casos, por exemplo, a <b + e <c é equivalente a um - e <b <c - e.
Esta notação pode ser generalizada para qualquer número de condições: por exemplo, de 1 a 2 ≤ ≤ ... ≤ a n significa que um i ≤ um i 1 para i = 1, 2, ..., n - 1. Por transitivity, esta condição é equivalente a um i ≤ a j para qualquer um ≤ i ≤ j ≤ n.
Ao resolver as desigualdades usando a notação encadeada, é possível e às vezes necessário avaliar os termos de forma independente. Por exemplo, para resolver as desigualdades 4 x <2 x + 1 ≤ 3 x + 2, não será capaz de isolar X em qualquer uma parte da desigualdade através da adição ou subtracção. Em vez disso, é possível resolver 4 x <2 x 1 + e 2 + x 1 ≤ 3 x + 2 de forma independente, obtendo-se x <1/2 e x ≥ -1, respectivamente, que podem ser combinadas na solução final -1 ≤ x < 1/2.
Ocasionalmente, a notação é usada encadeado com desigualdades em direcções diferentes, caso em que o significado é a conjunção lógica das desigualdades entre os termos adjacentes. Por exemplo, uma <b> c ≤ d significa que a <b, b> c, e c ≤ d. Além do uso raro em matemática, esta notação existe em algumas linguagens de programação , como Python .
Representando as desigualdades na linha de número real
Cada desigualdade (exceto aqueles que envolvem números imaginários) pode ser representada sobre o real linha de número mostrando regiões escuras na linha.
As desigualdades entre os meios
Há muitas desigualdades entre os meios. Por exemplo, para todos os números positivos 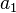 ,
, 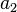 , ...,
, ..., 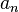
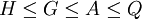 , Onde
, Onde
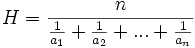 ( média harmônica),
( média harmônica),
![G = \ sqrt [n] {a_1 \ cdot a_2 \ cdot ... \ cdot a_n}](../../images/99/9944.png) ( média geométrica),
( média geométrica),
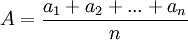 ( média aritmética ),
( média aritmética ),
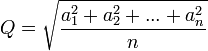 ( quadrático).
( quadrático).
As desigualdades de poder
Às vezes, com a notação "desigualdade de poder" compreender as desigualdades que contêm 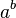 Tipo de expressões onde
Tipo de expressões onde 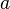 e
e 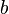 são reais números positivos ou expressões de algumas variáveis. Eles podem aparecer em exercícios de olimpíadas matemáticas e alguns cálculos.
são reais números positivos ou expressões de algumas variáveis. Eles podem aparecer em exercícios de olimpíadas matemáticas e alguns cálculos.
Exemplos
- Se
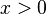 , Então
, Então 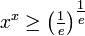
- Se
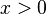 , Então
, Então 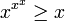
- Se
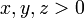 , Então
, Então 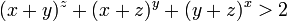 .
. - Para todos os números reais distintos
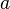 e
e 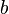 ,
, 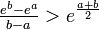
- Se
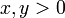 e
e 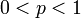 , Então
, Então 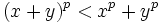
- Se
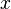 ,
, 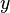 e
e 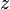 são positivos, então
são positivos, então 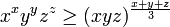
- Se
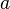 e
e 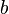 são positivos, então
são positivos, então 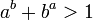 . Este resultado foi generalizado por R. Ozols em 2002, que provou que, se
. Este resultado foi generalizado por R. Ozols em 2002, que provou que, se 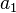 ,
, 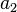 , ...,
, ..., 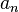 são quaisquer números reais positivos, em seguida,
são quaisquer números reais positivos, em seguida, 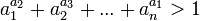 (Resultado está publicado na trimestral populares-científico letão o céu estrelado, ver referências).
(Resultado está publicado na trimestral populares-científico letão o céu estrelado, ver referências).
Desigualdades conhecidos
Veja também lista de desigualdades.
Os matemáticos usam frequentemente as desigualdades ligadas às quantidades para as quais fórmulas exatas não podem ser computados facilmente. Algumas desigualdades são utilizados com tanta frequência que eles têm nomes:
- A desigualdade de Azuma
- Desigualdade de Bernoulli
- Desigualdade de Boole
- Desigualdade de Cauchy-Schwarz
- Desigualdade de Chebyshev
- A desigualdade de Chernoff
- Desigualdade Cramér-Rao
- A desigualdade de Hoeffding
- A desigualdade de Hölder
- Desigualdade de aritmética e geométrica meios
- Desigualdade de Jensen
- A desigualdade de Kolgomorov
- A desigualdade de Markov
- Desigualdade de Minkowski
- A desigualdade de Nesbitt
- A desigualdade de Pedoe
- Da desigualdade do triângulo
Mnemônicos para estudantes
Jovens estudantes às vezes confundem a menos que e maior do que sinais, que são imagens de espelho um do outro. Uma mnemônica comumente ensinou é que o signo representa a boca de um faminto jacaré que está tentando comer o maior número; Deste modo, abre-se para 8 em ambos 3 <8 e 8> 3. Outro método é perceber os maiores pontos de quantidade à quantidade menor e diz: "ha-ha, eu sou maior do que você."
Além disso, em uma linha horizontal número, o sinal de maior que é a seta que está no fim da linha de maior número. Da mesma forma, a menos que o símbolo representa a seta na extremidade mais pequena do linha número (<--- 0--1--2--3--4--5--6--7--8--9 --->).
Os símbolos podem também ser interpretadas directamente a partir de sua forma - a lado com uma grande separação vertical indica a (r) grande quantidade, e o lado que é um ponto indica um pequeno (er) quantidade. Deste modo, os símbolos de desigualdade são semelhantes ao musical crescendo e decrescendo. Os símbolos para a igualdade, a menos-que-ou-igual-a, e maiores-que-ou-igual-a também pode ser interpretado com essa perspectiva.
Os números complexos e desigualdades
Com a introdução de um ordem lexicographical nos números complexos , é um totalmente ordenado conjunto. No entanto, é impossível definir ≤ modo que 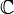 , +, *, Torna-se uma ≤ campo ordenada. Se
, +, *, Torna-se uma ≤ campo ordenada. Se 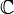 , +, *, ≤ eram um corpo ordenado, tem que satisfazer as duas seguintes propriedades:
, +, *, ≤ eram um corpo ordenado, tem que satisfazer as duas seguintes propriedades:
- Se um ≤ b + c, em seguida, uma ≤ b + c
- se ≤ 0 e um 0 ≤ b ≤ 0, em seguida, ab
Porque é um ≤ ordem total, para qualquer número um, uma ≤ 0 ou 0 ≤ a. Em ambos os casos ≤ 0 a 2; Isso significa que 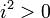 e
e 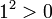 ; assim
; assim 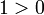 e
e 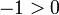 , Contradição.
, Contradição.
No entanto ≤ pode ser definida, a fim de satisfazer a primeira propriedade, ou seja, se uma ≤ b + c, em seguida, uma ≤ b + c. Uma definição que é por vezes utilizado é a ordem lexicográfica:
- um ≤ b se
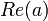 <
< 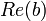 ou (
ou ( 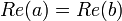 e
e 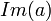 ≤
≤ 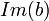 )
)
Pode ser facilmente demonstrado que para a definição de um ≤ b + c, em seguida, uma ≤ b + c

