
Interpolação
Sobre este escolas selecção Wikipedia
Crianças SOS tentou tornar o conteúdo mais acessível Wikipedia por esta selecção escolas. Visite o site da SOS Children at http://www.soschildren.org/
Na matemática de subcampo análise numérica, interpolação é um método de construção de novos pontos de dados dentro da gama de um conjunto discreto de pontos de dados conhecidos.
Na engenharia e ciência um frequentemente tem um número de pontos de dados, tal como obtido por amostragem ou experiência, e tenta construir uma função que se encaixa perto essas pontos de dados. Isto é chamado montagem ou curva de análise de regressão . A interpolação é um caso específico de ajuste de curva, em que a função deve ir exactamente através dos pontos de dados.
Um problema diferente, que está intimamente relacionado com a interpolação é a aproximação de uma função complicada por uma função simples. Suponha que nós sabemos a função, mas é demasiado complexo para avaliar de forma eficiente. Então nós poderíamos escolher um poucos pontos de dados conhecidos da função complicada, criando um Tabela de pesquisa, e tentar interpolar esses pontos de dados para construir uma função mais simples. Claro que, ao utilizar a função simples para calcular os novos pontos de dados que geralmente não recebem o mesmo resultado que quando utilizar a função original, mas, dependendo do domínio do problema eo método de interpolação utilizado o ganho em simplicidade pode compensar o erro.
Refira-se que existe um outro tipo muito diferente de interpolação em matemática, ou seja, o " interpolação dos operadores ". Os resultados clássicos sobre a interpolação de operadores são o Riesz-Thorin eo teorema Marcinkiewicz teorema. Há também muitos outros resultados subseqüentes.
Definição
De entre significado e entre pólo, os pontos ou nós. Qualquer forma de cálculo de um novo ponto entre dois pontos de dados existentes é, portanto, de interpolação.
Existem muitos métodos para fazer isso, muitos dos quais envolvem montagem algum tipo de função aos dados e avaliar essa função no ponto desejado. Isto não exclui outros meios, tais como métodos estatísticos de cálculo de dados interpolados.
A forma mais simples de interpolação é tomar a média das 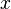 e
e 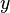 de dois pontos adjacentes para encontrar o ponto médio. Isto dará o mesmo resultado que a interpolação linear avaliada no ponto médio.
de dois pontos adjacentes para encontrar o ponto médio. Isto dará o mesmo resultado que a interpolação linear avaliada no ponto médio.
Dada uma seqüência de n números distintos x k chamados de nós e para cada x k um segundo número y k, estamos à procura de uma função f de modo a que
Um par x k, y k é chamado de ponto de dados e f é chamado de interpolação para os pontos de dados.
Quando o número y k são dadas por uma função conhecida f, que às vezes escrever f k.
Exemplo
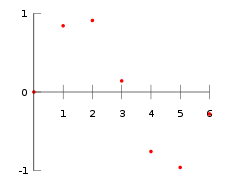
Por exemplo, suponha que temos uma tabela como esta, que dá alguns valores de uma função desconhecida f.
| x | f (x) | ||||
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 1 | 0 | . | 8415 | ||
| 2 | 0 | . | 9093 | ||
| 3 | 0 | . | 1411 | ||
| 4 | -0 | . | 7568 | ||
| 5 | -0 | . | 9589 | ||
| 6 | -0 | . | 2794 | ||
Interpolação proporciona um meio para estimar a função em pontos intermédios, tais como x = 2,5.
Existem muitos métodos de interpolação diferentes, alguns dos quais são descritos abaixo. Algumas das preocupações a ter em conta ao escolher uma adequada algoritmo são: Qual é a precisão do método? Como caro é? Como suave é a interpolação? Quantos dados são necessários pontos?
Piecewise interpolação constante
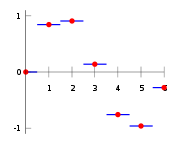
O método de interpolação mais simples é para localizar o valor de dados mais próxima, e atribuir o mesmo valor. Em uma dimensão, raramente há boas razões para escolher este sobre interpolação linear, que é quase tão barato, mas em dimensões mais elevadas, em interpolação multivariada, esta pode ser uma escolha favorável para a sua velocidade e simplicidade.
Interpolação linear
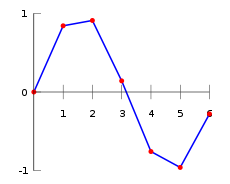
Um dos métodos mais simples é interpolação linear (às vezes conhecido como Lerp). Considere o exemplo acima de determinação de f (2.5). Uma vez que está a meio caminho entre 2,5 2 e 3, é razoável assumir F (2,5) a meio caminho entre f (2) = 0,9093 e F (3) = 0,1411, que produz 0,5252.
Geralmente, a interpolação linear leva dois pontos de dados, dizer (xa, y a) e (b x, y b), e a interpolação é dada por:
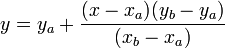 no ponto (x, y).
no ponto (x, y).
Interpolação linear é rápido e fácil, mas não é muito preciso. Outra desvantagem é que a interpolação não é diferenciável no ponto x k.
O seguinte estimativa de erro mostra que a interpolação linear não é muito precisa. Denotar a função que queremos interpolar por g, e suponha que x situa-se entre um e x x b e que g é duas vezes continuamente diferenciável. Em seguida, o erro de interpolação linear
Em outras palavras, o erro é proporcional ao quadrado da distância entre os pontos de dados. O erro de alguns outros métodos, incluindo interpolação polinomial e interpolação de spline (descrito abaixo), é proporcional às potências mais elevadas de a distância entre os pontos de dados. Estes métodos também produzem interpolants mais suaves.
Interpolação polinomial
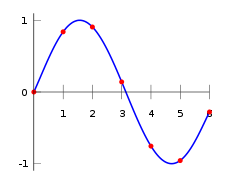
Interpolação de polinômios é uma generalização de interpolação linear. Note-se que a interpolação linear é um função linear. Nós agora substituir esta interpolação por um polinômio de maior grau.
Considerar outra vez o problema acima referido. O seguinte sexto grau polinomial passa por todos os sete pontos:
Substituindo x = 2.5, vemos que f (2,5) = 0,5965.
Geralmente, se temos pontos de n dados, há exatamente um polinômio de grau no máximo n -1 passando por todos os pontos de dados. A interpolação de erro é proporcional à distância entre os pontos de dados para a energia n. Além disso, a interpolação é um polinômio e assim infinitamente diferenciável. Assim, vemos que a interpolação polinomial resolve todos os problemas de interpolação linear.
No entanto, interpolação polinomial também tem algumas desvantagens. Calculando o polinômio interpolando é relativamente muito caro computacionalmente (veja complexidade computacional). Além disso, a interpolação polinomial podem não ser tão exacto apesar de tudo, especialmente nos pontos finais (ver O fenômeno de Runge). Estas desvantagens podem ser evitadas usando interpolação de spline.
Interpolação Spline
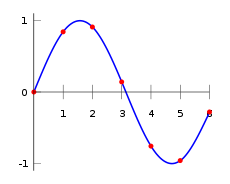
Recordar que a interpolação linear utiliza uma função linear para cada um dos intervalos de [x k, x k + 1]. Interpolação Spline utiliza polinômios de baixo grau em cada um dos intervalos, e escolhe as peças polinomiais de tal forma que eles se encaixam perfeitamente em conjunto. A função resultante é chamada uma spline.
Por exemplo, a spline cúbica natural é piecewise cúbicos e duas vezes continuamente diferenciável. Além disso, a sua segunda derivada é zero nos pontos finais. O spline cúbico natural, interpolando os pontos na tabela acima é dada por
Neste caso temos f (2,5) = 0,597262.
Como interpolação polinomial, interpolação de spline incorre um erro menor do que a interpolação linear ea interpolação é mais suave. No entanto, a interpolação é mais fácil avaliar que os polinómios de alto grau utilizados na interpolação polinomial. Ele também não sofre O fenômeno de Runge.
Outras formas de interpolação
Outras formas de interpolação pode ser construída recolhendo uma classe diferente de interpolants. Por exemplo, interpolação racional é interpolação por funções racionais, e interpolação trigonométrica é interpolação por polinômios trigonométricas. A transformada discreta de Fourier é um caso especial de interpolação trigonométrica. Outra possibilidade é usar wavelets.
O Whittaker-Shannon fórmula interpolação pode ser usado se o número de pontos de dados é infinita.
Interpolação multivariada é a interpolação das funções de mais de uma variável. Os métodos incluem interpolação bilinear e interpolação bicubic em duas dimensões, e interpolação trilinear em três dimensões.
Às vezes, sabemos não só o valor da função que queremos interpolar, em alguns pontos, mas também o seu derivado. Isto leva a Problemas de interpolação de Hermite.
Conceitos Relacionados
O termo extrapolação é utilizada, se quisermos encontrar pontos de dados fora do intervalo de pontos de dados conhecidos.
Em curva de problemas de montagem, a restrição de que a interpolação tem que ir exatamente através dos pontos de dados é descontraído. Só é necessária a aproximação de pontos de dados, tanto quanto possível. Isso requer parametrizar os potenciais interpolants e ter alguma forma de medir o erro. No caso mais simples isto leva a menos quadrados aproximação.
Estudos de teoria da aproximação como encontrar a melhor aproximação a uma determinada função por outra função de alguma classe pré-determinado, e como boa esta aproximação é. Isso produz claramente um limite de quão bem a interpolação pode aproximar a função desconhecida.

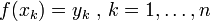
![| F (x) -g (x) | \ le C (x_b-x_a) ^ 2 \ quad \ mbox {onde} \ quad C = \ frac18 \ max_ {y \ in [x_a, x_b]} | g '' (y) |.](../../images/71/7171.png)
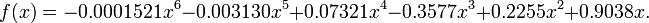
![f (x) = \ \ deixou {\ begin {matrix} -0,1522 x ^ 3 + 0,9937 x, & \ mbox {if} x \ in [0,1], \\ -,01258 x ^ 3-0,4189 x ^ 2 + 1,4126 x - 0,1396, & \ mbox {if} x \ in [1,2], \\ 0,1403 x ^ 3-1,3359 x ^ 2 + 3,2467 x - 1,3623, & \ mbox {if} x \ in [2, 3], \\ 0,1579 x ^ 3-1,4945 x ^ 2 + 3,7225 x - 1,8381, & \ mbox {if} x \ in [3,4], \\ 0,05375 x ^ 3 -0,2450 x ^ 2-1,2756 x + 4,8259, & \ mbox {if} x \ in [4,5], \\ -0,1871 x ^ 3 + 3,3673 x ^ 2-19,3370 x + 34,9282, & \ mbox {if} x \ in [5,6]. \\ \ End {matrix} \ right.](../../images/71/7182.png)
