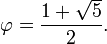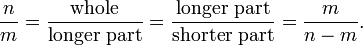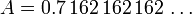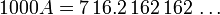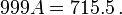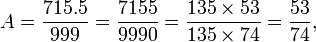Número irracional

Em matemática , um número irracional é qualquer número real que não é um número racional - isto é, é um número que não pode ser expressa como uma fracção de m / n, onde m e n são números inteiros , com n diferente de zero. Informalmente, isto significa que os números não podem ser representados como fracções simples. Pode-se deduzir que eles também não pode ser representado como terminação ou decimais repetir, mas a idéia é mais profunda do que isso. Embora possa parecer estranho à primeira audiência, quase todos os números reais são irracionais, em um sentido que é definido mais precisamente abaixo. Talvez os números mais conhecidos são irracional π e √2.

Quando o razão de comprimentos de dois segmentos de linha é irracional, os segmentos de linhas são também descritos como sendo incomensurável, o que significa que eles compartilham nenhuma medida em comum. Uma medida de um segmento de recta que, neste sentido, é um segmento de recta que J "medidas" I no sentido de que um número inteiro de cópias de J definidas ponta-a-ponta ocupar o mesmo comprimento que eu.

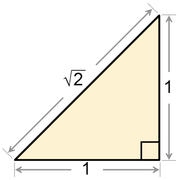
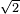O número é irracional.

História

A primeira prova da existência de números irracionais é geralmente atribuída a Hippasus de Metapontum, um Pitagórica que provavelmente descobri-los, identificando os lados do pentagrama. No entanto Pitágoras acreditava na incondicionalidade de números, e não podia aceitar a existência de números irracionais. Ele não podia negar a sua existência através da lógica, mas suas crenças não aceitaria a existência de números irracionais e assim, como a lenda tinha, ele tinha Hippasus afogado. Theodorus de Cirene provou a irracionalidade do surds de números inteiros até 17, mas parou por aí, provavelmente, porque a álgebra que ele usou não poderia ser aplicada para a raiz quadrada de 17. Não foi até Eudoxus desenvolveu uma teoria de relações irracionais que uma forte base matemática dos números irracionais foi criado. Elementos de Euclides Livro 10 é dedicado à classificação de magnitudes irracionais.

O século XVI viu a aceitação de negativos , integrais e fracionários números. O século XVII viu frações decimais com a notação moderna bastante geralmente usado por matemáticos. Os próximos cem anos viu os números imaginários se tornar uma ferramenta poderosa nas mãos de Abraham de Moivre e, especialmente, de Leonhard Euler . A conclusão da teoria de números complexos no século XIX, implicou a diferenciação dos irracionais em números algébricos e transcendentes, a prova da existência de números transcendentais, eo ressurgimento do estudo científico da teoria da irracionais, largamente ignorado desde Euclides . O ano de 1872 viu a publicação das teorias de Karl Weierstrass (por seu aluno Kossak), Heine ( Crelle, 74), Georg Cantor (Annalen, 5), e Richard Dedekind. Meray tinha tomado em 1869 o mesmo ponto de partida, Heine, mas a teoria é geralmente referido o ano 1872. método de Weierstrass foi completamente estabelecido pela Salvatore Pincherle em 1880, e de Dedekind tem recebido destaque adicional através do trabalho do autor mais tarde (1888) ea recente aprovação pelo Paul Tannery (1894). Weierstrass, Cantor e Heine baseiam suas teorias sobre séries infinitas, enquanto Dedekind funda sua sobre a ideia de um cortar (Schnitt) no sistema de números reais , separando todas números racionais em dois grupos tendo certas propriedades características. O assunto tem recebido contribuições posteriores nas mãos de Weierstrass, Kronecker (Crelle, 101), e Meray.

Frações contínuas, estreitamente relacionadas com números irracionais (e devido a Cataldi, 1613), recebeu atenção nas mãos de Euler , e no início do século XIX, foram trazidos à proeminência através dos escritos de Lagrange . Dirichlet também adicionado à teoria geral, assim como inúmeros contribuintes para as aplicações do assunto.

Lambert mostrou (1761) que π não pode ser racional, e que o e ⁿ é irracional se n é racional (a menos que n = 0). Enquanto a prova de Lambert é frequentemente dito ser incompleta, avaliações modernos apoiá-lo como satisfatória, e na verdade para seu tempo excepcionalmente rigoroso. Legendre (1794), após a introdução do Função de Bessel-Clifford, fornecida uma prova para mostrar que π ² é irracional, de onde segue-se imediatamente que π é irracional também. A existência de números transcendentes foi estabelecido pela primeira vez por Liouville (1844, 1851). Mais tarde, Georg Cantor (1873) provaram a sua existência por um método diferente, que mostrou que a cada intervalo nos reais contém números transcendentais. Charles Hermite (1873) provou primeiro transcendental, e Ferdinand von Lindemann (1882), partindo de conclusões de Hermite, mostrou o mesmo para π. A prova de Lindemann foi muito simplificada por Weierstrass (1885), ainda mais por David Hilbert (1893), e foi finalmente feita por elementar Adolf Hurwitz e Paul Albert Gordan.

Exemplo provas

A raiz quadrada de 2

A irracionalidade do raiz quadrada de 2 pode ser provado por assumindo que é racional e inferir uma contradição, chamado de um argumento por reductio ad absurdum. O seguinte argumento apela duas vezes para o fato de que o quadrado de um inteiro ímpar é sempre estranho.

Se √ 2 é racional tem a forma de m / n de números inteiros m, n não tanto mesmo. Então m ² = 2 n ² onde m é ainda, dizer m = 2 p. Assim 4 p = 2 ² n ² de modo 2 p = ² n ² de onde n é também até mesmo, uma contradição.

Outra prova

A seguir argumento reductio ad absurdum é menos conhecido. Ele usa as informações adicionais √2> 1.

1. Assume-se que √2 é um número racional. Isto significa que existem inteiros m e n com n ≠ 0 tal que m / n = √2.
2. Então √2 também pode ser escrita como uma fração irredutível m / n com números inteiros positivos, porque √2> 0.
3. Em seguida 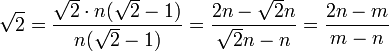, Porque .
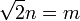4. Desde √2> 1, segue-se que m> n, que por sua vez implica que m> 2 n - m.
5. Assim, a fracção m / n para √2, que de acordo com (2) já está Em termos mais baixo, é representado por (3) em termos estritamente inferiores. Isso é uma contradição, então a suposição de que √2 é racional deve ser falsa.

Da mesma forma, assumir um triângulo isósceles cuja perna direita e hipotenusa ter os respectivos comprimentos de n e m inteiros. Pelo teorema de Pitágoras , a relação m / n é igual a √2. É possível construir por um clássico régua e compasso construção de um triângulo isósceles direito menores cuja perna e hipotenusa ter respectivos comprimentos m - n 2 e n - m. Que a construção comprova a irracionalidade da √2 pelo tipo de método que foi contratado por geômetras gregos antigos.

A raiz quadrada de 10 e além

Se √ 10 é racional, dizem m / n, em seguida, m ² = 10 n ^2. No entanto, em notação decimal, cada quadrado termina em um mesmo número de zeros. Então, em seguida, m ² e 10 n ² em decimal deve terminar em, respectivamente, um número par e ímpar de zeros, uma contradição.

De modo mais geral, em qualquer r raiz que não é em si um quadrado, cada quadrado termina em um mesmo número de zeros, de onde √ 10 _r na raiz r é irracional, ou seja, √ r é irracional. Segue-se que os únicos números inteiros com raízes quadradas racionais são quadrados. Como um caso em apreço, 2 não é um quadrado, e dois em binário é de 10 _2. (Nota da convenção de subscripting números não decimais, com sua raiz, para evitar ambiguidades. Como parte dessa convenção os subscritos são entendidos como sendo em decimal, não sendo eles próprios subscrita.)

Para ir ainda mais longe, podemos considerar m ^k = r × n ^k para qualquer inteiros e r k. Se r u ^k ≠ para qualquer número inteiro de u, então o símbolo R tem pelo menos um factor primo p aumentada para um expoente que não é divisível por k. Como todos os expoentes da fatoração em primos de m ^k são divisíveis por k, para a equação de segurar, o primeiro-factorização de n ^k deve conter p elevado a uma potência que também não é divisível por k. Mas isso é claramente impossível. Assim, para qualquer inteiros e R k, ^k √ r é irracional se r u ^k ≠ para qualquer número inteiro u. Esse resultado também decorre do fato de que o aumento um número racional não-integral a um poder integrante nunca pode igualar um inteiro além de 1.

A relação dourada

Quando um segmento de linha é dividida em dois subsegmentos disjuntos de tal maneira que a proporção de toda a parte mais longa é igual à razão entre a maior parte da parte mais curta, em seguida, que é o rácio razão de ouro , igual

Suponha que este é um número racional n / m em termos mais baixos. Aqui n para ter o comprimento de toda a m e o comprimento da parte mais longa. Em seguida, n> m, e o comprimento da parte mais curta é n - m. Então nós temos

No entanto, isso coloca uma fração menor em termos já em termos mais baixas -a contradição. Portanto, a suposição inicial, que a proporção áurea é racional, é falsa.

Logaritmos

Talvez os números mais facilmente provado ser irracional certas logaritmos . Aqui está uma prova por reductio ad absurdum que log ₂ 3 é irracional:

• Suponha log ₂ 3 é racional. Para alguns inteiros positivos m e n, temos log ₂ 3 = m / n.
• Segue-se que 2 ^{m / n} = 3.
• Levante cada lado para o poder n, encontrar 2 ^{m n} = 3.
• Mas 2 para qualquer potência de número inteiro maior do que 0 é ainda (porque, pelo menos, um dos seus factores primos é 2) e 3 a qualquer potência de número inteiro maior do que 0 é impar (porque nenhum dos seus factores primos é 2), de modo que o pressuposto inicial é falsa.

Casos como log ₁₀ 2 podem ser tratados de modo semelhante.

Irracionais transcendentais e algébricas

Quase todos os números irracionais são transcendentais e todos números transcendentes são irracionais: o artigo sobre números transcendentes lista vários exemplos e ^r e ^r π são irracionais se r ≠ 0 é racional; e também ^π é irracional..

Outra maneira de construir números irracionais é tão irracional números algébricos, ou seja, como zeros de polinômios com coeficientes inteiros: começar com uma equação polinomial

p (x) = a _n x ⁿ + um _n x ⁿ _-1 ^-1 + ... + a ₁ x + a = ₀ 0

em que os coeficientes a _i são números inteiros. Suponha que você sabe que existe algum número real x com p (x) = 0 (por exemplo, se n é ímpar e um _n é diferente de zero, em seguida, por causa da valor intermediário teorema). As únicas raízes racionais possíveis desta equação polinomial são da forma r / s, onde r é um divisor de um ₀ e s é um divisor de um _n; há apenas um número finito de tais candidatos, que você pode tudo cheque à mão. Se nenhum deles é raiz de p, então x deve ser irracional. Por exemplo, esta técnica pode ser utilizada para mostrar que x = (2 ^1/2 + 1) ^1/3 é irracional: temos (x ^{3-1) 2} = 2 e, por conseguinte, x ^6-2 x ^3-1 = 0 e esta última polinomial não possui raízes racionais (os únicos candidatos a verificar são ± 1).

Uma vez que os números algébricos formar um campo, muitos números irracionais pode ser construído através da combinação de números transcendentes e algébricas. Por exemplo 3π + 2, + π √ 2 e 3 e √ são irracionais (e até mesmo transcendental).

Expansões decimais

A expansão decimal de um número irracional nunca se repete ou termina, ao contrário de um número racional.

Para mostrar isso, vamos supor que dividir inteiros n por m (onde m é diferente de zero). Quando divisão longa é aplicado à divisão de n por m, apenas são possíveis restos de m. Se 0 aparece como um resto, a expansão decimal termina. Se 0 nunca ocorre, em seguida, o algoritmo pode correr no máximo m - 1 passos sem utilização de qualquer remanescente mais do que uma vez. Depois disso, a restante deve se repetir, e, em seguida, as repetições de expansão decimais!

Por outro lado, suponha que estamos diante de um decimal recorrente, podemos provar que é uma fração de dois inteiros. Por exemplo:

Aqui o comprimento da repitend é 3. multiplicar por 10 ^3:

Note-se que desde que multiplicado por 10 elevado à potência do comprimento da parte repetindo, nós deslocamos os dígitos à esquerda do ponto decimal exactamente por que muitas posições. Portanto, o fim da cauda de 1000 A corresponde ao fim da cauda de um exatamente. Aqui, a administração de 1000 A e A têm repetindo 162 no final.

Portanto, quando nós subtraímos A partir de ambos os lados, o fim da cauda de 1000 A cancela para fora da extremidade da cauda de um:

Em seguida

que é um quociente de inteiros e, por conseguinte, um número racional.

Perguntas abertas

Não se sabe se π + e ou π - e é irracional ou não. Na verdade, não há nenhum par de inteiros diferentes de zero m e n para o qual não se souber se m π + ne é irracional ou não. Além disso, não se sabe se o conjunto {π, e} é algebricamente independente sobre Q.

Não se sabe se a 2 ^e, π ^e, π ^√2, Constante do catalão, ou o Euler-Mascheroni γ constante o valor de gama são irracionais.

O conjunto de todos os irracionais

Uma vez que os reais formar um conjunto incontável de que os números racionais são um subconjunto contável, o conjunto complementar de irracionais é incontável.

De acordo com o habitual ( Euclidiana) função distância d (x, y) = | x - y |, os números reais são um espaço métrico e, portanto, também uma espaço topológico. Restringindo a função de distância euclidiana dá os irracionais a estrutura de um espaço métrico. Uma vez que o subespaço de irracionais não está fechada, a métrica induzida não é completa. No entanto, ser um Conjunto G-delta - ou seja, uma interseção contável de subconjuntos abertos - em um espaço métrico completo, o espaço de irracionais é topologicamente completo, ou seja, existe uma métrica nas irracionais induzindo a mesma topologia como a restrição da métrica Euclidiana, mas com respeito às quais os irracionais estão completos. Pode-se ver isso sem saber o já mencionado fato sobre conjuntos G-delta: a expansão fracção contínua de um número irracional define um homeomorphism a partir do espaço de irracionais para o espaço de todas as sequências de números inteiros positivos, o que é facilmente visto para ser completamente metrizável.

Além disso, o conjunto de todos os irracionais é um espaço métrico desconectado.