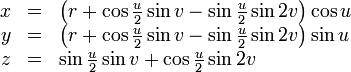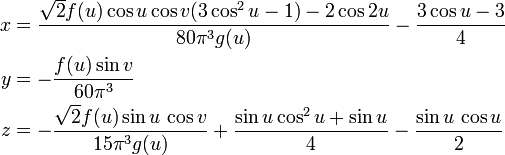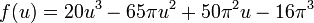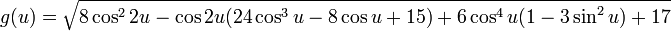Garrafa de Klein
Informações de fundo
Crianças SOS oferecem um download completo desta seleção para as escolas para uso em escolas intranets. Todas as crianças disponíveis para apadrinhamento de crianças de Crianças SOS são cuidadas em uma casa de família pela caridade. Leia mais ...

Em matemática , a garrafa de Klein é um certo não- orientável superfície, ou seja, uma superfície (um bidimensional espaço topológico) sem e lados distintos "internos" "exteriores". Outros objetos não-orientáveis relacionadas incluem o Fita de Möbius ea plano projetivo real. Considerando que uma fita de Möbius é um objeto bidimensional com um dos lados e uma borda, uma garrafa de Klein é um objeto tridimensional com um lado e sem arestas. (Para fins de comparação, uma esfera é um objecto tridimensional, sem arestas e dois lados).
A garrafa de Klein foi descrita pela primeira vez em 1882 pelo alemão matemático Felix Klein. Ele foi originalmente chamado de "superfície Klein" Kleinsche Fläche; no entanto, isso foi interpretado incorretamente como Kleinsche Flasche "garrafa de Klein", o que levou à adopção da presente termo em língua alemã também.
Construção
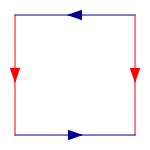
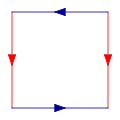
Comece com um quadrado, e em seguida, cole em conjunto correspondente bordas coloridas, no diagrama a seguir, de modo que as setas jogo. Mais formalmente, a garrafa de Klein é o espaço quociente descrito como o quadrado [0,1] x [0,1] com lados identificados pelas relações (0, y) ~ (1, y) para y 0 ≤ ≤ 1 e (x, 0) ~ (1 - x, 1) para 0 ≤ x ≤ 1:
Esta praça é uma polígono fundamental da garrafa de Klein.
Note-se que esta é uma "abstrato" colagem no sentido de que a tentar perceber isso em três dimensões resulta em uma garrafa de Klein auto-interseção. A garrafa de Klein, propriamente dita, não se auto-interseção. No entanto, há uma maneira de visualizar a garrafa de Klein como sendo contido em quatro dimensões.
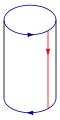
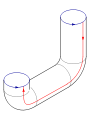
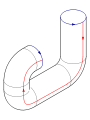
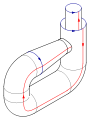
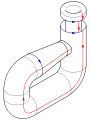
Cole as setas vermelhas do quadrado juntos (lados esquerdo e direito), resultando em um cilindro. Para colar as extremidades em conjunto para que as setas no jogo círculos, passar um final através do lado do cilindro. Observe que isso cria um círculo de auto-intersecção. Isto é um imersão da garrafa de Klein em três dimensões.
Ao adicionar uma quarta dimensão para o espaço tridimensional, a auto-cruzamento pode ser eliminado. Gradualmente empurrar uma parte do tubo que contém a intersecção para fora do espaço original tridimensional. Uma analogia útil é considerar uma curva de auto-intersecção no plano; auto-intersecções pode ser eliminado por uma cadeia de elevação ao lado do avião.
Esta imersão é útil para a visualização de muitas propriedades da garrafa de Klein. Por exemplo, a garrafa de Klein não tem limite, onde a superfície pára abruptamente, e é não orientável, como refletido na unilateralidade da imersão.

O modelo físico comum de uma garrafa de Klein é uma construção semelhante. O Museu da Ciência britânico tem em exposição uma colecção de vidro soprado à mão garrafas de Klein, exibindo muitas variações sobre este tema topológico. As garrafas datam de 1995 e foram feitas para o museu por Alan Bennett. Clifford Stoll, autor de Ovo do cuco, fabrica e vende garrafas de Klein-los através da Internet em Acme Klein Bottle.
Propriedades
A garrafa de Klein pode ser visto como um feixe de fibras como segue: toma-se o quadrado de cima é E, o espaço total, enquanto que o espaço de base B é dado pelo intervalo unitário em x, e a projecção π é dada por π (x, y) = x. Uma vez que os dois extremos do intervalo x na unidade são identificados, o espaço base B é, na verdade, o círculo S 1, e assim a garrafa de Klein é torcido a S 1 -bundle ( círculo bundle) sobre o círculo.
Como o Fita de Möbius, a garrafa de Klein é um diferenciável bidimensional colector que não é orientável. Ao contrário da fita de Möbius, a garrafa de Klein é uma variedade fechada, o que significa que é um compacto colector sem limite. Enquanto a fita de Möbius pode ser incorporado em tridimensional espaço euclidiano R 3, a garrafa de Klein não pode. Pode ser incorporado em R4, no entanto.
A garrafa de Klein pode ser construído (no sentido matemático, porque ele não pode ser feito sem permitir que a superfície a cortar a si mesmo), unindo as extremidades de duas tiras de Möbius em conjunto, tal como descrito na seguinte anônima Limerick :
- Um matemático chamado Klein
- Pensei que a banda de Möbius foi divino.
- Disse ele: "Se você cola
- As bordas das duas,
- Você obterá uma garrafa estranho como o meu. "
Também pode ser construído por dobragem de uma tira de Moebius ao meio no sentido do comprimento e prendendo a ponta para si.
Seis cores suficiente para colorir qualquer mapa sobre a superfície de uma garrafa de Klein; esta é a única exceção à Heawood conjectura, uma generalização do teorema das quatro cores , o que exigiria sete.
Uma garrafa de Klein é equivalente a uma esfera mais dois tampões transversais.
Dissecação
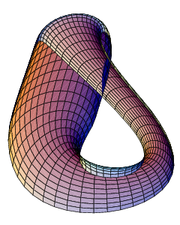
Dissecando uma garrafa de Klein em metades ao longo de seu plano de simetria resulta dois no espelho Tiras de Möbius, ou seja, um com uma meia-torção canhota e outro com uma meia-torção destro (um deles é retratado à direita). Lembre-se que o cruzamento na foto não está realmente lá. Na verdade, também é possível cortar a garrafa de Klein em uma única fita de Moebius.
Parametrização
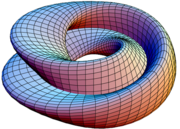
A "figura 8" imersão da garrafa de Klein tem uma parametrização particularmente simples:
Neste imersão, o círculo de auto-interseção é um geométrico círculo no plano xy. A constante positivo r é o raio do círculo. O parâmetro L dá o ângulo no plano XY, e v especifica a posição em torno da secção transversal em forma de 8.
A parametrização da imersão 3-dimensional da própria garrafa é muito mais complicado. Aqui está uma versão simplificada:
onde
para 0 ≤ u <2π e 0 ≤ v <2π.
Neste parametrização, u segue o comprimento do corpo da garrafa, enquanto v passa em torno da sua circunferência.
Generalizações
A generalização da garrafa de Klein para maior género é dada no artigo sobre o polígono fundamental.
Klein superfície
Uma superfície Klein é, como para superfícies de Riemann , uma superfície com um atlas permitindo que o funções de transição pode ser composto com uma conjugação complexa pode obtém a chamada estrutura dianalytic.