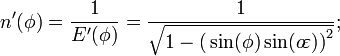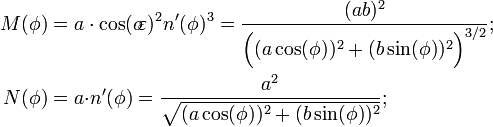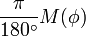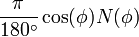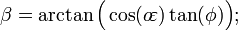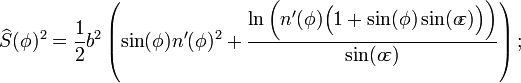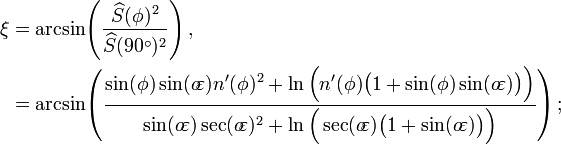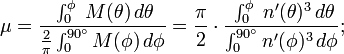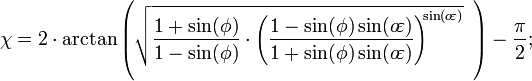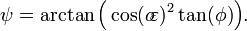Latitude

Assuntos Relacionados: Matemática

Sobre este escolas selecção Wikipedia

Esta seleção é feita para as escolas de caridade infantil leia mais . Clique aqui para saber mais sobre apadrinhamento de crianças.

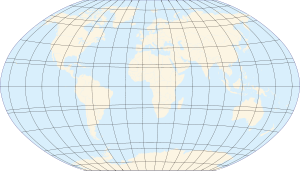Mapa de Terra

Longitude (λ)

Linhas de longitude aparecem vertical com variados curvatura nessa projeção, mas na verdade são metades de grandes elipses, com raios idênticos em um determinado latitude.

Latitude (φ)

As linhas de latitude aparecem horizontal com curvatura variável nesta projecção; mas, na verdade, são circulares com raios diferentes. Todos os locais com uma determinada latitude são referidos coletivamente como um Paralelo .

O equador divide o planeta em uma Hemisfério Norte e um Hemisfério Sul, e tem uma latitude de 0 °.

Geodésia
Fundamentos
Geodésia Geodinâmica Geomatics Cartografia
Conceitos
Dado Distância Geoid Figo. Terra Sistema geodésico Geodésico Geog. coord. sistema Hor. pos. representar. Lat. / Grandes. Mapa proj. Ref. elipsóide Geodesia Satélite Ref espacial. sistema
Technologies
GNSS GPS GLONASS Galileo Bússola
Padrões
ED50 ETRS89 GRS 80 NAD83 NAVD88 SAD69 SRID UTM WGS84
História
História da geodesia NAVD29

Latitude, usualmente representada simbolicamente pela letra grega phi, 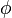$\ Phi \, \!$ , Dá a localização de um lugar na Terra (ou outro corpo planetário) ao norte ou ao sul do equador . Linhas de Latitude são as linhas horizontais mostradas executando leste-à-oeste em mapas. Tecnicamente, a latitude é uma medida angular em graus (marcado com °) variando de 0 ° no equador (latitude baixo) a 90 ° com os pólos (90 ° N para o North Pole ou 90 ° S para a Pólo Sul; alta latitude). O ângulo complementar da latitude é chamado o colatitude.

Círculos de latitude

Todos os locais de uma determinada latitude são referidos coletivamente como um Paralelo ou linha de latitude ou em paralelo, porque eles são coplanar, e todos esses planos são paralelo ao equador . As linhas de latitude diferentes do Equador são aproximadamente pequenos círculos na superfície da terra; eles não são geodésicas desde o caminho mais curto entre dois pontos na mesma latitude envolve mover mais longe, em seguida, em direção, o equador (veja grande círculo).

Entrar no norte Vermont.

Uma latitude específico pode então ser combinado com um específico longitude para definir uma posição precisa sobre a superfície da Terra (ver sistema de navegação por satélite).

Importantes círculos chamados de latitude

Além do equador, outras quatro linhas de latitude são nomeados por causa do papel que desempenham na relação geométrica com a Terra eo Sol:

Arctic Circle - 66 ° 33 '39 "N
Trópico de Câncer - 23 ° 26 '21 "N
Trópico de Capricórnio - 23 ° 26 '21 "S
Antarctic Circle - 66 ° 33 '39 "S

Apenas em latitudes entre os trópicos é possível que o sol estar no zênite. Apenas ao norte do Círculo Ártico ou ao sul do Antarctic Circle é o sol possível meia-noite.

A razão que estas linhas têm os valores que eles fazem, está na inclinação do eixo da Terra em relação ao sol, que é 23 ° 26 '21,41 " .

Note que o Círculo Ártico e Trópico de Câncer eo Círculo Polar Antártico e Trópico de Capricórnio são colatitudes já que a soma de seus ângulos é de 90 °.

Subdivisões

Para simplificar os cálculos, onde consideração elíptica não é importante, a milha náutica foi criada, igualando exatamente 111,12 quilômetros por grau de arco ou, sub-dividindo-se em minutos, 1852 metros por minuto de arco. Um minuto de latitude pode ser dividido em 60 segundos. Uma latitude é assim definida como 13 ° 19'43 "N (para maior precisão, uma fracção decimal pode ser adicionado aos segundos). Uma representação alternativa usa apenas graus e minutos, em que os segundos são expressos como uma fração decimal de minutos, assim, o exemplo acima é expressa como 13 Degrees ° 19.717 'N. também pode ser expressa singularmente, com ambos os minutos e segundos constituídas na forma de um número decimal e arredondado como desejado (notação decimal grau): 13,32861 ° N. Às vezes, a norte / sul sufixo é substituído por um sinal negativo para o sul (-90 ° para a Pólo Sul).

Efeito da latitude

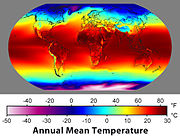
As temperaturas médias variam fortemente com a latitude.

A latitude da região tem um grande efeito sobre o seu clima e tempo (ver Efeito do ângulo do sol no clima ). Latitude mais frouxamente determina tendências em auroras polares, ventos predominantes, e outras características físicas de localizações geográficas.

Pesquisadores da Centro de Harvard para o Desenvolvimento Internacional (CID) encontrados em 2001 que apenas três tropicais economias - Hong Kong , Singapura e Taiwan - foram classificados como de alta renda pelo Banco Mundial, embora todos os países dentro das regiões zoneado como temperado teve economias ou média ou de alta renda.

Parâmetros elípticas

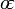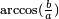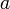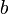Porque a maioria dos planetas (incluindo a Terra) são elipsóides de revolução, ou esferóides, em vez de esferas , tanto o raio e o comprimento do arco varia com a latitude. Esta variação exige a introdução de parâmetros elípticas baseado em uma elipse de excentricidade angular, $o \! \ varepsilon \, \!$ (Que é igual $\ Scriptstyle {\ arccos (\ frac {b} {a})} \, \!$ , Onde $um \; \!$ e $b \; \!$ são os raios equatoriais e polares; 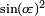${(! 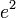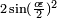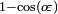O \ \ varepsilon) \ pecado ^ 2} \ scriptstyle \; \!$ é o primeiro excentricidade ao quadrado, ${E ^ 2} \; \!$ ; e $\ Scriptstyle {2 \ sin (\ frac {o \ \ varepsilon} {2}!) ^ 2} \; \!$ ou $\ Scriptstyle {1- \ cos (! O \ \ varepsilon)} \; \!$ é o aplanar, 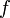${F} \; \!$ ). Utilizada na criação das integrandos para curvatura é o inverso da diretor integrando elíptica, $E '\; \!$ :

$n '(\ phi) = \ frac {1} {E' (\ phi)} = \ frac {1} {\ sqrt {1- \ grande (\ sin (\ phi) \ sin (o \! \ varepsilon) \ grande) ^ 2}}; \, \!$

$\begin{align}M(\phi)&=a\cdot\cos(o\!\varepsilon)^2n'(\phi)^3=\frac{(ab)^2}{\Big((a\cos(\phi))^2+(b\sin(\phi))^2\Big)^{3/2}};\\ N (\ phi) & = a {\ cdot} n '(\ phi) = \ frac {a ^ 2} {\ sqrt {(A \ cos (\ phi)) ^ 2 + (b \ sin (\ phi) ) ^ 2}}; \ end {align} \, \!$

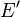Comprimento grau

O comprimento de um arcdegree de latitude (norte-sul) é de cerca de 60 milhas náuticas, 111 km ou 69 milhas terrestres em qualquer latitude. O comprimento de um arcdegree de longitude (leste-oeste) no equador é aproximadamente o mesmo, reduzindo a zero nos pólos.

No caso de um esferóide, uma meridiano e seu anti-meridiano formar uma elipse , a partir do qual uma expressão exata para o comprimento de um arcdegree de latitude é:

$\ Frac {\ pi} {180 ^ \ circ} M (\ phi) \; \!$

Este raio de curvatura (ou "arcradius") está localizado no plano de um meridiano, e é conhecido como o meridional raio de curvatura, 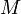$M \; \!$ .

Da mesma forma, uma expressão exacta para o comprimento de um arcdegree da longitude é:

$\ Frac {\ pi} {180 ^ \ circ} \ cos (\ phi) N (\ phi) \; \!$

O arcradius aqui contida é no plano do vertical, o avião leste-oeste principal perpendicular (ou " normal ") para ambos o plano do meridiano e o plano tangente à superfície do elipsóide, e é conhecido como o raio de curvatura normais, 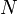$N \; \!$ .

Ao longo do equador (leste-oeste), 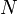$N \; \!$ é igual ao raio equatorial. O raio de curvatura numa ângulo certo para o equador (norte-sul), 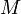$M \; \!$ , Cerca de 43 km mais curto, por conseguinte, o comprimento de um arcdegree de latitude no equador é cerca de 1 km menos do que o comprimento de um arcdegree de longitude no equador. Os raios de curvatura são iguais nos pólos, onde eles são cerca de 64 km maior do que o raio equatorial norte-sul de curvatura, porque o raio polar é 21 km menos do que o raio equatorial. Os raios polares mais curtos indicam que os hemisférios norte e sul são mais planas, fazendo com que seus raios de curvatura mais tempo. Esse achatamento também 'pitadas' o raio equatorial norte-sul de curvatura, tornando-se 43 km menos do que o raio equatorial. Ambos os raios de curvatura são perpendiculares ao plano tangente à superfície do elipsóide em todas as latitudes, dirigido para um ponto sobre o eixo polar no hemisfério oposto (excepto no equador onde ambos apontam para o centro da Terra). O raio leste-oeste de curvatura atinge o eixo, enquanto que o raio norte-sul de curvatura é menor em todas as latitudes, exceto os pólos.

O Elipsóide WGS84, utilizado por todos Dispositivos de GPS, utiliza um raio equatorial de 6.378.137,0 m e um achatamento inversa, (1 / f), de 298,257223563, daí o seu raio polar é 6356752,3142 m e sua primeira excentricidade quadrado é 0,00669437999014. O mais recente, mas pouco usado IERS elipsóide 2003 fornece raios equatorial e polar de 6.378.136,6 6.356.751,9 e m, respectivamente, e um inverso do achatamento de 298,25642. Comprimentos de graus sobre os elipsóides WGS84 e iers 2003 são os mesmos quando arredondados para seis algarismos significativos. Uma calculadora apropriada para qualquer latitude é fornecido por os EUA governo de Agência Nacional de Inteligência Geoespacial (NGA).

Latitude	Raio NS de curvatura, 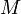$M \; \!$	Grau de latitude	Raio EW de curvatura, 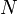$N \; \!$	Grau de longitude
0 °	6.335,44 km	110,574 km	6.378,14 km	111,320 km
15 °	6.339,70 km	110,649 km	6.379,57 km	107,551 km
30 °	6.351,38 km	110,852 km	6.383,48 km	96,486 km
45 °	6.367,38 km	111,132 km	6.388,84 km	78,847 km
60 °	6.383,45 km	111,412 km	6.394,21 km	55,800 km
75 °	6.395,26 km	111,618 km	6.398,15 km	28,902 km
90 °	6.399,59 km	111,694 km	6.399,59 km	0,000 km

Tipos de latitude

Com um esferóide que está ligeiramente achatadas pela sua rotação, cartografia referem-se a uma variedade de latitudes auxiliares para se adaptar precisamente projecções esféricas de acordo com a sua finalidade.
Para fins que não a Terra planetas, como Marte , latitude geográfica e geocêntrica são chamados de "planetographic" e "planetocentric" latitude, respectivamente. A maioria dos mapas de Marte desde 2002 coordenadas uso planetocentric.

Comum "latitude"

No uso comum, "latitude" refere-se a latitude geodésica ou geográfica 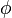$\ Phi \, \!$ e é o ângulo entre o plano equatorial e uma linha que é normal à referência esferóide, que aproxima a forma da Terra para explicar achatamento dos pólos e abaulamento do equador.

As expressões a seguir assumir secções elípticas polares e que todos os cortes paralelos ao plano equatorial são circulares. Latitude geográfica (com longitude), em seguida, fornece uma Gauss.

Latitude reduzida

Reduzido ou latitude paramétrico, 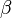$\ Beta \, \!$ , É a latitude do mesmo raio da esfera com o mesmo equador.

$\ Beta = \ arctan \ Big (\ cos (o \ \ varepsilon) \ tan (\ phi) \ Big!); \, \!$

Latitude authalic

Latitude authalic, 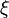$\ Xi \, \!$ , Dá uma transformação para a esfera preservando-área.

$\widehat{S}(\phi)^2=\frac{1}{2}b^2\left(\sin(\phi)n'(\phi)^2+\frac{\ln\bigg(n'(\phi)\Big(1+\sin(\phi)\sin(o\!\varepsilon)\Big)\bigg)}{\sin(o\!\varepsilon)}\right);\,\!$

$\ Begin {align} \ xi & = \ arcsin \! \ Left (\ frac {\ widehat {s} (\ phi) ^ 2} {\ widehat {s} (90 ^ \ circ) ^ 2} \ right), \ \ &=\arcsin\!\left(\frac{\sin(\phi)\sin(o\!\varepsilon)n'(\phi)^2+\ln\Big(n'(\phi)\big(1+\sin(\phi)\sin(o\!\varepsilon)\big)\Big)}{\sin(o\!\varepsilon)\sec(o\!\varepsilon)^2+\ln\Big(\sec(o\!\varepsilon)\big(1+\sin(o\!\varepsilon)\big)\Big)}\right);\end{align}\,\!$

Latitude retificação

Retificação latitude, 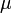$\ Mu \, \!$ , É a distância da superfície do equador, dimensionado de modo que o pólo é 90 °, mas envolve a integração elíptica:

$\ Mu = \ frac {\; \ int_ {0} ^ \ phi \; M (\ theta) \, d \ theta} {\ frac {2} {\ pi} \ int_ {0} ^ {90 ^ \ circ } M (\ phi) \, d \ phi} =\frac{\pi}{2}\cdot\frac{\;\int_{0}^\phi\;n'(\theta)^3\,d\theta}{\int_{0}^{90^\circ}n'(\phi)^3\,d\phi};\,\!$

Latitude Conformal

Latitude conformada, 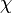$\ Chi \, \!$ , Dá uma de preservação ângulo ( conformal) transformar à esfera.

$\chi=2\cdot\arctan\left(\sqrt{\frac{1+\sin(\phi)}{1-\sin(\phi)}\cdot\left(\frac{1-\sin(\phi)\sin(o\!\varepsilon)}{1+\sin(\phi)\sin(o\!\varepsilon)}\right)^{\!\!\sin(o\!\varepsilon)}}^{\color{white}|}\;\right)-\frac{\pi}{2};\;\!$

Latitude geocêntrica

A latitude geocêntrica, 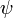$\ Psi \, \!$ , É o ângulo entre o plano equatorial e uma linha a partir do centro da Terra.

$\ Psi = \ arctan \ Big (\ cos (o \ \ varepsilon) ^ 2 \ tan (\ phi) \ Big!) \;. \!$

Comparação de latitudes

A trama a seguir mostra as diferenças entre os tipos de latitude. Os dados utilizados encontra-se na tabela seguinte da trama. Por favor, note que os valores na tabela são em minutos, não graus, eo enredo reflete isso também. Observe também que os símbolos de conformação estão escondidos atrás do geocêntrico devido a estar muito perto do valor.

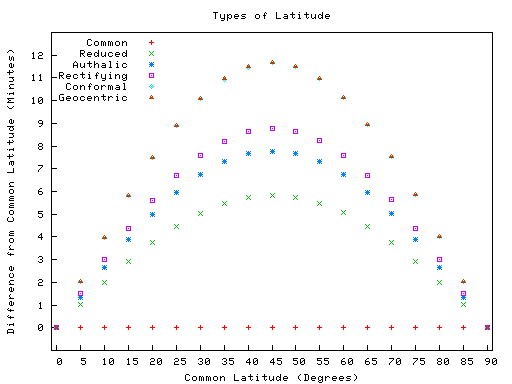
Tipos de latitude Difference.png

Diferença aproximada de latitude geográfica ("Lat")
Lat 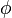$\ Phi \, \!$	Reduzido 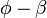$\ Tropia \ beta \, \!$	Authalic 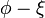$\ Tropia \ xi \, \!$	Retificação 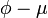$\ Tropia \ mu \, \!$	Conformal 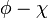$\ Tropia \ chi \, \!$	Geocêntrico 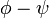$\ Tropia \ psi \, \!$
0 °	0.00 '	0.00 '	0.00 '	0.00 '	0.00 '
5 °	1.01 '	1.35 '	1.52 '	2.02 '	2.02 '
10 °	1.99 '	2.66 '	2.99 '	3,98 '	3,98 '
15 °	2.91 '	3,89 '	4,37 '	5,82 '	5,82 '
20 °	3.75 '	5.00 '	5,62 '	7,48 '	7,48 '
25 °	4,47 '	5,96 '	6,70 '	8,92 '	8,92 '
30 °	5.05 '	6,73 '	7,57 '	10.09 '	10.09 '
35 °	5,48 '	7,31 '	8,22 '	10,95 '	10,96 '
40 °	5.75 '	7,66 '	8,62 '	11.48 '	11.49 '
45 °	5,84 '	7,78 '	8,76 '	11.67 '	11.67 '
50 °	5.75 '	7,67 '	8,63 '	11.50 '	11.50 '
55 °	5,49 '	7,32 '	8,23 '	10.97 '	10.98 '
60 °	5,06 '	6.75 '	7,59 '	10.12 '	10.13 '
65 °	4,48 '	5,97 '	6,72 '	8,95 '	8,96 '
70 °	3,76 '	5.01 '	5,64 '	7,52 '	7,52 '
75 °	2.92 '	3.90 '	4,39 '	5.85 '	5.85 '
80 °	2,00 '	2.67 '	3.00 '	4.00 '	4.01 '
85 °	1.02 '	1.35 '	1.52 '	2.03 '	2.03 '
90 °	0.00 '	0.00 '	0.00 '	0.00 '	0.00 '

Latitude astronômica

Uma medida mais obscuro de latitude é a latitude astronômica, que é o ângulo entre o plano equatorial ea normal ao geóide (ou seja, um fio de prumo). Originou-se como o ângulo entre horizonte e estrela polar.

Latitude astronômica não deve ser confundido com declinação, a coordenar astrônomos usam para descrever os locais de estrelas norte / sul do equador celeste (ver coordenadas equatorial), nem com latitude eclíptica, a coordenada que os astrônomos utilizam para descrever os locais de estrelas norte / sul do eclíptica (veja coordenadas eclíptica).

Palæolatitude

Continentes mover ao longo do tempo, devido às deriva continental, qualquer que seja tomada fósseis e outras características de interesse que possam ter com eles. Particularmente quando se discute fósseis, muitas vezes é mais útil para saber onde o fóssil foi quando foi estabelecido, de onde ele é quando ele foi desenterrado: isso é chamado de palæolatitude do fóssil. O Palæolatitude pode ser restringida por dados paleomagnéticos. Se grãos magnetizáveis minúsculos estão presentes quando a rocha está sendo formado, estes irão se alinhar com o campo magnético da Terra como agulhas de bússola. A magnetómetro pode deduzir a orientação destes grãos submetendo uma amostra a um campo magnético, e a declinação magnética dos grãos pode ser usada para inferir a latitude de deposição.

Correções para a altitude

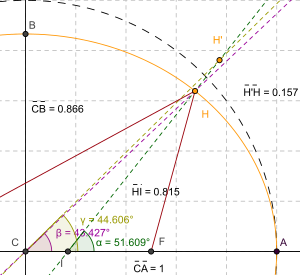
Linha IH é normal para o esferóide no ponto H. O ângulo que forma com o equador corresponde a latitude geodésica.

Ao converter de geodésica ("comum") latitude, as correções devem ser feitas para altitude para sistemas que não medem o ângulo do normal do esferóide. Na figura à direita, ponto H (localizado na superfície do esferóide) e ponto H '(localizado em algum maior elevação) têm diferentes latitudes geocêntrico (ângulos β e γ, respectivamente), embora eles compartilham a mesma latitude geodésica (ângulo α). (Note-se que o achatamento do esferóide e a elevação do ponto H 'é significativamente maior do que aquilo que é encontrado na Terra, exagerar os erros normalmente encontrados em tais cálculos).

Retirado de " http://en.wikipedia.org/w/index.php?title=Latitude&oldid=196912178 "