Projeção de mapa

A projeção Mercator mostra cursos de rolamento constante como linhas retas.

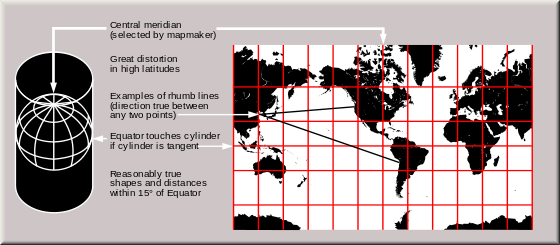
Uma projeção de mapa é todo o método utilizado no cartografia para representar o bidimensional curvada superfície da terra ou outro corpo em um avião .

O termo " projeção "aqui se refere a qualquer função definida sobre a superfície da Terra e com os valores no avião, e não necessariamente um geométrico de projeção.

Apartamento mapas não poderia existir sem projeções, porque uma esfera não podem ser deitadas sobre um plano sem distorções. Pode-se ver isso matematicamente como conseqüência de Gauss de Theorema Egregium. Mapas planos pode ser mais útil do que globos em muitas situações: eles são mais compactos e fáceis de armazenar; eles prontamente acomodar uma enorme gama de escalas; eles são vistos facilmente em monitores de computador; eles podem facilitar propriedades do terreno a ser mapeada de medição; eles podem mostrar grandes porções da superfície da Terra ao mesmo tempo; e eles são mais baratos para produzir e transportar. Estes traços úteis de mapas planos motivar o desenvolvimento de projeções de mapa.

Propriedades métricas de mapas

Muitas propriedades podem ser medidos na superfície da terra, independentemente de sua geografia. Algumas destas propriedades são as seguintes:

Um Projeção Albers mostra áreas com precisão, mas distorce formas.

• Área
• Forma
• Direção
• Rolamento
• Distância
• Escala

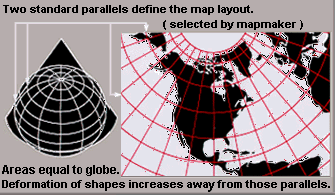
Projeções do mapa pode ser construída para preservar uma ou algumas dessas propriedades, embora nem todos eles simultaneamente. Cada projeção preserva ou compromissos ou aproxima propriedades métricas básicas de maneiras diferentes. A finalidade do mapa, em seguida, determina qual projecção deve formar a base para o mapa. Desde existem muitos propósitos para os mapas, assim como muitas projeções existem sobre a qual construí-los.

Outra preocupação importante que dirige a escolha de uma projecção é o grau de compatibilidade de conjuntos de dados. Os conjuntos de dados são a informação geográfica. Como tal, a sua recolha depende do modelo escolhido para a terra. Diferentes modelos atribuir ligeiramente diferentes coordenadas para o mesmo local, por isso, é importante que o modelo seja conhecido e que projecção escolhido seja compatível com esse modelo. Em pequenas áreas problemas de compatibilidade de dados (em grande escala) são mais importantes desde distorções métricas são mínimas, a este nível. Em áreas muito grandes (em pequena escala), por outro lado, a distorção é um factor mais importante a considerar.

Construção de uma projeção de mapa

A criação de uma projeção de mapa envolve três passos:

1. A selecção de um modelo para a forma da terra ou corpo planetário (geralmente escolher entre uma esfera ou elipsóide)
2. Transformação de coordenadas geográficas ( longitude e latitude ) para coordenadas planas ( Eastings e northings ou x, y)
3. Redução da escala (não interessa em que ordem os segundo e terceiro passos são executados)

Devido a forma da terra real é irregular, a informação é perdida no primeiro passo, em que um de aproximação, modelo regular é escolhido. Reduzindo a escala pode ser considerada como fazendo parte de coordenadas geográficas para transformar coordenadas planas.

A maioria das projeções de mapa, prático e teórico, não são "projeções" em qualquer sentido físico. Em vez disso, eles dependem de matemática fórmulas que não têm interpretação física direta. No entanto, para a compreensão do conceito de uma projeção de mapa é útil pensar em um globo com uma fonte de luz colocada em algum definitiva ponto em relação a ele, que se projecta características do globo sobre uma superfície. A discussão a seguir de superfícies evolutivas baseia-se no conceito de que.

Escolhendo uma superfície de projecção

A Projeção cilíndrica Miller mapeia o globo em um cilindro.

A superfície que pode ser desdobrada ou desenrolada em uma superfície plana ou folha sem alongamento, rasgar ou encolhendo é chamado de ' superfície developable '. O cilindro, cone e, claro, o avião são todas as superfícies developable. A esfera e elipsóide não são superfícies developable. Qualquer projecção que tenta projectar uma esfera (ou um elipsóide) sobre uma folha plana terá para distorcer a imagem (semelhante à impossibilidade de fabrico de uma folha plana de uma casca de laranja).

Uma maneira de descrever uma projecção é em primeiro lugar para projectar a partir da superfície da terra a uma superfície revelável tal como um cilindro ou cone, seguido por um segundo passo simples de desenrolamento da superfície em um plano. Enquanto o primeiro passo inevitavelmente distorce algumas propriedades do globo, a superfície developable pode, então, ser desdobrado sem mais distorção.

A orientação da projecção

Este Mercator projecção transversal é matematicamente o mesmo que um Mercator padrão, mas orientado em torno de um eixo diferente.

Uma vez que é feita uma escolha entre a projectar sobre um cilindro, cone ou plano, a orientação da forma deve ser escolhido. A orientação é a forma como é colocada em relação ao globo. A orientação da superfície de projecção pode ser normal (em linha com o eixo da Terra), transversal (em ângulo reto com o eixo da Terra) ou oblíqua (qualquer ângulo entre eles). Estas superfícies podem também ser tangente ou secante para o globo esférico ou elipsoidal. Tangent significa que os toques de superfície, mas não cortar através do globo; secante significa a superfície faz fatia através do globo. Na medida em que preserva as propriedades métricas ir, nunca é vantajosa para mover a superfície developable longe do contato com o mundo, de modo que a prática não é discutida aqui.

Escala

A Globo é a única forma de representar a Terra com constante escalonar ao longo de todo o mapa em todas as direções. Um mapa não pode alcançar essa propriedade para qualquer área, não importa quão pequena. Ele pode, no entanto, atingir escala constante ao longo de linhas específicas.

Algumas propriedades possíveis são:

• A escala depende da localização, mas não na direção. Isto é equivalente a preservação de ângulos, a característica definidora de um mapa conformado.
• A escala é constante ao longo de qualquer paralelo na direcção do paralelo. Isto aplica-se para qualquer forma cilíndrica ou em projecção pseudocylindrical aspecto normal.
• Combinação dos anteriores: a escala depende da latitude apenas, não em longitude ou direção. Isto aplica-se para a projeção Mercator no aspecto normal.
• A escala é constante ao longo de todas as linhas retas que irradiam a partir de duas localizações geográficas específicas. Esta é a característica definidora de uma projecção equidistante, como o Azimutal equidistante projeção ou o Projeção Equirectangular.

A escolha de um modelo para a forma da Terra

Construção de projecção é também afectada pelo modo como a forma de a terra é aproximada. Na sequência da discussão sobre as categorias de projeção, uma esfera é assumido. No entanto, a Terra não é exatamente esférica, mas está mais próximo em forma para um oblato elipsóide, uma forma que protrai em torno do equador . Seleccionar um modelo para uma forma da terra envolve a escolha entre as vantagens e desvantagens de uma esfera contra um elipsóide. Modelos esféricos são úteis para os mapas de pequena escala, como atlas mundiais e globos, uma vez que o erro nessa escala geralmente não é perceptível ou importantes o suficiente para justificar o uso do elipsóide mais complicado. O modelo elipsoidal é comumente usado para construir mapas topográficos e para outros mapas de grande e médio porte que precisam descrever com precisão a superfície da terra.

Um terceiro modelo da forma da terra é chamado um geóide, que é um complexo e representação mais ou menos preciso da superfície do nível do mar médio global que é obtido através de uma combinação de medições de gravidade terrestre e por satélite. Este modelo não é utilizada para o mapeamento, devido à sua complexidade, mas em vez disso é utilizado para fins de controlo, na construção de datums geográficos. (Em geodesia, plural de "dado" é "datums," em vez de "dados".) Um geóide é usado para construir um dado adicionando irregularidades ao elipsóide, a fim de melhor corresponder forma real da Terra (que leva em conta a características de grande escala no campo de gravidade da Terra associados padrões de convecção do manto, bem como as assinaturas de gravidade muito grandes características geomorfológicas, tais como cadeias de montanhas, planaltos e planícies). Historicamente, datums ter sido baseado em elipsóides que melhor representam o geóide na região do Datum pretende mapear. Cada elipsóide tem um eixo maior e menor distinta. Diferentes modificações controlos () são adicionados ao elipsóide, a fim de construir o ponto de referência, que é especializada para a regiões geográficas específicas (tais como o North American Datum). Alguns datums modernas, tais como WGS84 (o usado no Sistema de Posicionamento Global GPS), são otimizados para representar toda a terra, bem como possível com um único elipsóide, à custa de alguma precisão em regiões menores.

Classificação

A classificação fundamentais projeção é baseada no tipo de superfície de projeção sobre a qual o mundo está conceitualmente projetada. As projecções são descritas em termos da colocação de uma superfície gigante em contacto com a terra, seguido por uma operação de dimensionamento implícita. Estas superfícies são cilíndricos (por exemplo, Mercator ), cónica (por exemplo, Albers), e azimutal ou plano (por exemplo, estereográfica). Muitas projeções matemáticas, no entanto, não perfeitamente caber em qualquer um desses três métodos de projeção conceituais. Assim outras categorias de pares foram descritos na literatura, tais como pseudoconic (meridianos são arcos de círculos), pseudocylindrical (meridianos são linhas rectas), pseudoazimuthal, retroazimuthal, e policônica.

Outra forma de classificar projeções é através das propriedades que eles preservam apesar de projeção. Algumas das categorias mais comuns são:

• Preservar direção (azimutal), um traço possível apenas a partir de um ou dois pontos para todos os outros pontos
• Preservar forma localmente ( conformado ou orthomorphic)
• Área de preservação (-área igual ou equiareal ou equivalente ou authalic)
• Preservar a distância (equidistante), um traço possível apenas entre um ou dois pontos e todos os outros pontos
• Preservar a rota mais curta, um traço preservado apenas pela projeção gnomônica

NOTA: Devido a esfera não é uma superfície developable, é impossível construir uma projeção de mapa que é ao mesmo tempo-área igual e conformada.

Projeções da superfície

Cilíndrico

O projeção Mercator espaço-oblíqua foi desenvolvido pela USGS para uso em Imagens Landsat.

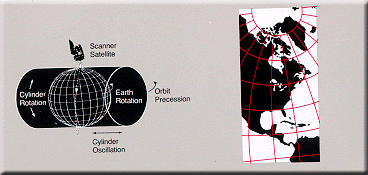
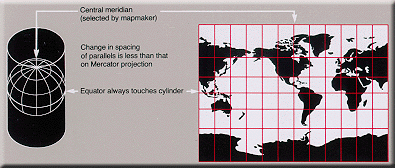
O termo "saliência cilíndrica" é utilizado para se referir a qualquer projecção em que meridianos são mapeados para igualmente espaçados linhas verticais e círculos de latitude (paralelos) são mapeados para linhas horizontais (ou, mutatis mutandis, mais geralmente, as linhas radiais a partir de um ponto fixo são mapeados para linhas paralelas equidistantes e círculos concêntricos em torno dele são mapeados para linhas perpendiculares).

O mapeamento dos meridianos às linhas verticais podem ser visualizadas por imaginando um cilindro (de que o eixo coincide com o eixo de rotação da Terra) enrolado em torno da Terra, e em seguida, se projecta no cilindro, e posteriormente desdobramento do cilindro.

Inevitavelmente, todas as projecções cilíndricas têm a mesma leste-oeste estendendo-se a partir do equador por um factor igual ao secante da latitude , em comparação com a escala no equador. As várias projecções cilíndricas pode ser descrita em termos de norte-sul alongamento:

• Norte-sul alongamento é igual ao alongamento leste-oeste (secante (L)): A escala leste-oeste corresponde à-sul-norte escala: cilíndrico conformada ou Mercator ; isso distorce áreas excessivamente em altas latitudes (ver também Transversa de Mercator).
• Norte-sul que se estende a crescer rapidamente com a latitude, ainda mais rápido do que o alongamento leste-oeste (secante (L)) ²: A perspectiva cilíndrico (= cilíndrica central) de projeção; porque distorção inadequada é ainda pior do que na projeção Mercator.
• Norte-sul alongamento cresce com a latitude, mas menos rapidamente do que o leste-oeste alongamento: como a Projecção cilíndrica Miller (secante (G * 4/5)).
• Distâncias norte-sul nem esticada nem comprimida (1): cilíndrica equidistante ou placa carrée.
• Norte-sul compressão precisamente o inverso do alongamento leste-oeste (cos (L)):-área igual cilíndrica (com muitas especializações nomeados como Gall-Peters ou Gall ortográfica, Behrman, e Lambert cilíndrico-área igual). Isto divide distâncias norte-sul por um fator igual ao secante da latitude, preservando área, mas fortemente distorcer formas.

No primeiro caso (Mercator), a escala leste-oeste é sempre igual a escala norte-sul. No segundo caso (cilíndrica central), a escala norte-sul supera a escala leste-oeste em todos os lugares longe do equador. Cada caso restante tem um par de latitudes idênticas de sinal contrário (ou então o equador) em que a escala leste-oeste corresponde à-sul-norte escala.

Projecções cilíndricas mapear toda a Terra como um retângulo finito, exceto nos dois primeiros casos, em que o retângulo se estende infinitamente alto, mantendo largura constante.

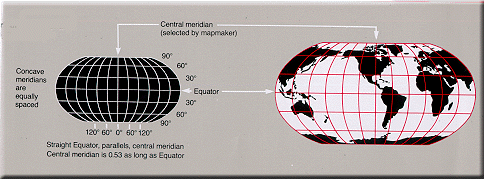
Pseudocylindrical

A projecção sinusoidal mostra os tamanhos relativos com precisão, mas grosseiramente distorce formas. A distorção pode ser reduzida por "interrupção" do mapa.

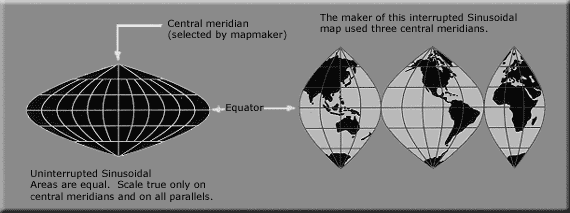
Projeções Pseudocylindrical representam o centro meridiano e cada paralelo como um único segmento de linha reta, mas não os outros meridianos. Cada projecção pseudocylindrical representa um ponto na terra ao longo da linha recta que representa o seu paralelo, a uma distância que é uma função da sua diferença de longitude a partir do meridiano central.

• Sinusoidal: a escala norte-sul ea escala leste-oeste são as mesmas em todo o mapa, criar um mapa-área igual. No mapa, como, na realidade, o comprimento de cada paralelo é proporcional ao coseno da latitude. Assim, a forma do mapa de toda a terra é a área entre duas curvas cosseno rotacionados simétricas.

A distância real entre dois pontos na mesma meridiano corresponde à distância no mapa entre os dois paralelos, que é menor do que a distância entre os dois pontos no mapa. A verdadeira distância entre dois pontos no mesmo paralelo - eo verdadeiro espaço de formas no mapa - não são distorcidas. Os meridianos desenhados no mapa ajudar o utilizador a perceber a distorção da forma e compensar mentalmente para isso.

• Projeção Collignon, que em suas formas mais comuns representa cada meridiano como dois segmentos de linha reta, um de cada pólo ao equador.
• Mollweide
• Goode homolosine
• Eckert IV

• Eckert VI

• Kavrayskiy VII
• Tobler hyperelliptical

Híbrido

O Projeção HEALPix combina uma projeção cilíndrica-área igual nas regiões equatoriais com o Collignon projecção em áreas polares.

Cônico

• Cônica equidistante
• Lambert conformal cônica
• Albers cônica

Pseudoconical

• Bonne
• Werner cordiform designa um pólo e um meridiano; distâncias do pólo são preservados, assim como distâncias do meridiano (que é em linha reta) ao longo dos paralelos
• Contínuo Policônica americana

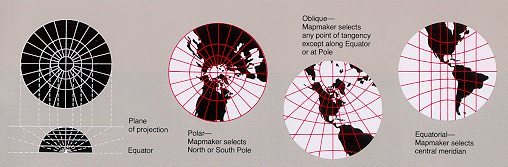
Azimutal (projeções sobre um plano)

Uma projeção azimutal mostra distâncias e direções com precisão a partir do ponto central, mas distorce as formas e tamanhos em outros lugares.

Projeções azimutais têm a propriedade de que a partir de um ponto central são preservados (e, portanto, grandes círculos através do ponto central são representados por linhas retas no mapa). Normalmente, estas saliências têm simetria radial também nas escalas e, portanto, nas distorções: Mapa de distâncias a partir do ponto central são calculadas por uma função de r (d) do verdadeiro distância d, independente do ângulo; correspondentemente, círculos com o ponto central como centro são mapeados em círculos que têm como centro o ponto central no mapa.

O mapeamento das linhas radiais podem ser visualizados por imaginar um plano tangente à Terra, com o ponto central como ponto de tangência.

A escala é radial r »(d) e o r escala transversal (d) / (r sen (d / R)) em que R é o raio da Terra.

Algumas projeções azimutais são verdadeiras perspectiva projeções; isto é, eles podem ser construídos mecanicamente, que se projecta da superfície da Terra por linhas que se estendem a partir de um Os pontos de perspectiva (ao longo de uma linha infinita através do ponto tangente eo ponto tangente de antípoda) para o avião:

• O Displays de projeção gnomónico grandes círculos como linhas retas. Pode ser construído utilizando um ponto de vista no centro da Terra R (d) = C tan (d / I).; um hemisfério já exige um mapa infinito,
• O Projecção Perspectiva Geral pode ser construído usando um ponto de perspectiva do lado de fora da terra. As fotografias da Terra (como os da Estação Espacial Internacional ) dar essa perspectiva.
• O projeção ortográfica mapeia cada ponto da Terra para o ponto mais próximo do avião. Pode ser construído a partir de um ponto de perspectiva de uma distância infinita do ponto tangente; R (d) = C sin (d / R). Pode exibir até um hemisfério em um círculo finito. Fotografias de Terra de longe o suficiente, como a Lua , dar a esta perspectiva.
• A projecção conformada azimutal, também conhecido como o stereographic projecção, pode ser construído usando o ponto de tangente antípoda como o ponto de perspectiva r (d) = C tan (d / 2 I).; a escala é c / (2 R cos² (d / 2 R)). Pode exibir quase toda a esfera em um círculo finito. A esfera completa requer um mapa infinito.

Outras projeções azimutais não são verdadeiras projeções de perspectiva:

• Equidistante azimutal: r (d) = cd; é usado por operadores de rádio amador para saber a direção para apontar suas antenas em direção a um ponto e ver a distância para ele. Distância a partir do ponto de tangência no mapa é proporcional à distância sobre a superfície da terra (; para o caso em que o ponto de tangente é o pólo norte, ver o bandeira das Nações Unidas)
• Lambert-azimutal área igual. Distância do ponto de tangência no mapa é proporcional à distância em linha reta através da terra: r (d) = c sin (d / 2 R)
• Azimutal logarítmica é construído de modo a que a distância de cada ponto de centro do mapa é o logaritmo da sua distância a partir do ponto de tangência na Terra. Funciona bem com mapas cognitivos R (d) = C In (d / d _0).; localizações mais perto do que a uma distância igual à constante d ₀ não são mostrados (figura 6-5)

Projeções da preservação de uma propriedade métrica

A projeção estereográfica é conformada e perspectiva, mas não igual área ou equidistante.

Conformal

Projeções do mapa conformados preservar ângulos localmente:

• Mercator - linhas de rumo são representados por segmentos retos
• Estereográfica - forma circular é conservada
• Roussilhe
• Lambert conformal cônica
• Mapa quincuncial
• Adams hemisfério-in-a-quadrado projeção
• Guyou hemisfério-in-a-quadrado projeção

-Área igual

A-área igual Projeção Mollweide

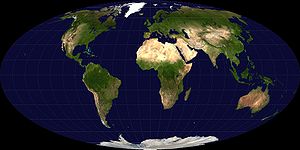
Estas projeções preservam a área:

Equidistante

Estes preservar distância de algum ponto ou linha padrão:

• Placa carrée - escala norte-sul é constante
• Equirectangular - distância igual entre todas as latitudes e longitudes.
• Equidistante azimutal - escala radial com respeito ao ponto central é constante

um de dois pontos projeção equidistante da Ásia

• Cônica equidistante
• sinusoidal - escala leste-oeste é constante e corresponde a distâncias entre os paralelos (mas a escala norte-sul longe do meridiano central é maior devido à obliqüidade dos meridianos)
• Distâncias cordiform Werner do Pólo Norte estão corretos assim como a distância curvada na paralelos
• Soldner
• Duas ponto eqüidistante: dois "pontos de controle" são arbitrariamente escolhido pelo fabricante de mapa. Distância a partir de qualquer ponto sobre o mapa para cada ponto de controlo é proporcional à distância sobre a superfície da terra.

Gnomónico

O Projeção gnomônica é pensado para ser a projeção do mapa mais antigo, desenvolvido pela Thales no Século 6 aC

Grandes círculos são exibidas como linhas retas:

• Projeção gnomônica

Retroazimuthal

Direcção a uma localização fixa B (o rolamento no local de partida A do percurso mais curto) corresponde à direcção no mapa a partir de A para B:

• Littrow - a única projeção conformal retroazimuthal
• Martelo retroazimuthal - também preserva a distância a partir do ponto central
• Craig retroazimuthal aka Meca ou Qibla - também tem meridianos verticais

Projeções de compromisso

O Projeção Robinson foi adotado por National Geographic revista em 1988, mas abandonado por eles em cerca de 1997 para a Winkel Tripel.

Projeções de compromisso desistir da idéia de perfeição preservando propriedades métricas, procurando em vez de encontrar um equilíbrio entre as distorções, ou simplesmente para fazer as coisas "parece certo". A maior parte destes tipos de projecções distorcem a forma nas regiões polares mais do que no equador:

• Robinson
• van der Grinten
• Miller cilíndrica
• Winkel Tripel
• Dymaxion de Buckminster Fuller
• Mapa da borboleta do BJS Cahill
• Mapa da borboleta de Steve Waterman
• Kavrayskiy VII
• Wagner VI

Outros notáveis projeções

• Chamberlin trimétrica
• O cartógrafo francês Oronce Belas desenvolveu uma projeção em forma de coração no século XVI