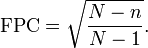Margem de erro
Fundo para as escolas Wikipédia
Esta seleção wikipedia foi escolhido por voluntários que ajudam Crianças SOS da Wikipedia para este Seleção Wikipedia para as escolas. SOS Children trabalha em 45 países africanos; você pode ajudar uma criança em África ?

A margem de erro é uma estatística que expressa a quantidade de aleatória erro de amostragem numa Os resultados da pesquisa. Quanto maior a margem de erro, a menos confiança deve-se ter que relataram os resultados da enquete são perto dos valores "verdadeiros"; isto é, os valores para o conjunto população.
Explicação
A margem de erro é normalmente definida como a raio de uma intervalo de confiança para um determinado estatística de um inquérito. Um exemplo é a porcentagem de pessoas que preferem produto A versus produto B. Quando uma única margem, global de erro é relatado para uma pesquisa, refere-se à margem de erro máxima para todas as relatadas percentagens utilizando a amostra total da pesquisa. Se a estatística é uma percentagem, esta margem de erro máxima pode ser calculada como o raio do intervalo de confiança para uma percentagem relatada de 50%.
A margem de erro tenha sido descrita como uma quantidade "absoluto", igual a um raio de intervalo de confiança para a estatística. Por exemplo, se o valor real é de 50 pontos percentuais, ea estatística tem uma confiança raio intervalo de 5 pontos percentuais, então dizemos que a margem de erro é de 5 pontos percentuais. Como outro exemplo, se o valor real é 50 pessoas, ea estatística tem uma confiança raio intervalo de 5 pessoas, então poderíamos dizer a margem de erro é de 5 pessoas.
Em alguns casos, a margem de erro não é expresso como uma quantidade "absoluto"; em vez disso, é expressa como uma quantidade "parente". Por exemplo, suponha que o valor real é 50 pessoas, ea estatística tem uma confiança raio intervalo de 5 pessoas. Se usarmos a definição "absoluto", a margem de erro seria de 5 pessoas. Se usarmos a definição "relativa", então nós expressamos esta margem de erro absoluto como uma percentagem do valor verdadeiro. Portanto, neste caso, a margem absoluta de erro é de 5 pessoas, mas a "percentagem relativa" margem de erro é de 10% (5 pessoas porque são dez por cento de 50 pessoas). Muitas vezes, porém, a distinção não é feita de forma explícita, mas normalmente resulta do contexto.
Tal como os intervalos de confiança, a margem de erro pode ser definida para qualquer nível de confiança desejado, mas geralmente um nível de 90%, 95% ou 99% é escolhida (geralmente 95%). Este nível é a probabilidade de que uma margem de erro em torno da percentagem relatado que incluem a percentagem "verdadeira". Junto com o nível de confiança, o desenho da amostra para um inquérito, e em particular a sua dimensão da amostra, determina a magnitude da margem de erro. Uma amostra maior produz uma menor margem de erro, tudo o mais permanecendo igual.
Se forem utilizados os intervalos exactos de confiança, em seguida, a margem de erro toma em conta tanto o erro de amostragem e de erro não-amostragem. Se um intervalo de confiança aproximado é utilizado (por exemplo, assumindo que a distribuição é normal e depois modelando o intervalo de confiança em conformidade), em seguida, a margem de erro pode ter apenas aleatório erro de amostragem em conta. Ela não representa outras fontes potenciais de erro ou viés, como um desenho da amostra não representativa, mal perguntas formuladas, as pessoas mentindo ou recusando-se a responder, a exclusão de pessoas que não puderam ser contatados, ou miscounts e erros de cálculo.
Conceito
Correr exemplo
Um exemplo de execução do Campanha presidencial de 2004 será utilizado para ilustrar os conceitos ao longo deste artigo. De acordo com um 2 de outubro de 2004 pesquisa realizada pela Newsweek, 47% dos eleitores inscritos votariam John Kerry / John Edwards se a eleição fosse realizado no mesmo dia, 45% votariam em George W. Bush / Dick Cheney, e 2% votariam Ralph Nader / Peter Camejo. O tamanho da amostra foi de 1,013. Salvo indicação em contrário, o resto do artigo utiliza um nível de 95% de confiança.
Conceito básico
Pesquisas envolvem tipicamente recolha de uma amostra a partir de uma determinada população. No caso da pesquisa da Newsweek, a população de interesse é a população de pessoas que vão votar. Porque é impraticável para pesquisar todos aqueles que irão votar, pesquisadores recolher amostras menores que se destinam a ser representativa; isto é, uma amostra aleatória da população. É possível que os pesquisadores provar 1.013 eleitores que acontecerá a votar em Bush, quando na verdade a população é dividida igualmente entre Bush e Kerry, mas isso é extremamente improvável (p = 2 -1.013 ≈ 1,13923782 × 10 -305), dado que a amostra é aleatória.
Teoria da amostragem proporciona métodos para calcular a probabilidade de que os resultados da pesquisa diferem da realidade por mais de um determinado montante, simplesmente devido ao acaso; por exemplo, que a pesquisa reporta 47% para Kerry, mas seu apoio é realmente tão alto quanto 50%, ou é realmente um preço tão baixo quanto 44%. Esta teoria e alguns Suposições Bayesian sugerem que a percentagem "true" será, provavelmente, bastante perto de 47%. Quanto mais as pessoas que estão incluídos na amostra, os pesquisadores mais confiantes pode ser que a percentagem "true" está perto da percentagem observada. A margem de erro é uma medida de quão perto os resultados são susceptíveis de ser.
No entanto, a margem de erro só é responsável por erro de amostragem aleatória, por isso é cego para erros sistemáticos que podem ser introduzidas por não-resposta ou por interações entre a pesquisa e memória, motivação, comunicação dos sujeitos e do conhecimento.
Cálculos assumindo amostragem aleatória
Esta seção irá discutir brevemente a erro padrão de uma percentagem, a correspondente intervalo de confiança, e conectar esses dois conceitos para a margem de erro. Para simplificar, os cálculos aqui assumir a pesquisa foi baseada em uma amostra aleatória simples a partir de uma grande população.
O erro padrão de um relataram proporção ou percentagem p mede a sua precisão, e é o desvio padrão estimado da referida percentagem. Ela pode ser calculada a partir apenas p e o tamanho da amostra, n, se n é pequeno em relação ao tamanho da população, com a seguinte fórmula:
- Erro padrão =
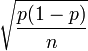
Quando a amostra não é um amostra aleatória simples a partir de uma grande população, o erro padrão eo intervalo de confiança deve ser estimado através de cálculos mais avançados. Na maioria dos casos, o intervalo de confiança verdadeira é aproximada assumindo a distribuição é normal, e entrando com o intervalo. Para as distribuições normais, os raios de intervalo de confiança é proporcional ao erro padrão. Normalmente, o verdadeiro erro padrão é desconhecido, assim o erro padrão de estimativa calculada a partir dos dados de exemplo.
Note-se que não há necessariamente uma ligação rígida entre o intervalo de confiança verdadeira, e o erro padrão verdadeiro. O intervalo de confiança por cento p-verdade é o intervalo [a, b] p que contém por cento da distribuição, e onde (100-P) / 2 por cento de distribuição encontra-se abaixo de um, e (100-P) / 2 por cento de a distribuição se encontra acima b. O erro padrão verdadeiro da estatística é a raiz quadrada da verdadeira variância de amostragem estatística. Estes dois não pode ser diretamente relacionado, embora, em geral, para as grandes distribuições que se parecem com curvas normais, não há uma relação direta.
Na pesquisa da Newsweek, o nível de apoio de Kerry p = 0,47 e n = 1.013. O erro padrão (016 ou 1,6%) ajuda a dar um sentido da precisão de percentagem estimada de Kerry (47%). A Interpretação bayesiana do erro padrão é que, embora não sabemos o percentual "true", é muito provável a ser localizado dentro de dois desvios-padrão da percentagem prevista (47%). O erro padrão pode ser usado para criar um intervalo de confiança de dentro do qual a percentagem "verdadeiro" deve ser o de um certo nível de confiança.
A percentagem estimada mais ou menos a sua margem de erro é de um intervalo de confiança para a porcentagem. Em outras palavras, a margem de erro é a metade da largura do intervalo de confiança. Ele pode ser calculado como um múltiplo do erro padrão, com o factor dependendo de o nível de confiança desejado; uma margem de erro de um padrão dá um intervalo de confiança de 68%, enquanto que a estimativa 1,96 erros padrão mais ou menos é um intervalo de confiança de 95%, e um intervalo de confiança de 99% funciona 2,58 erros padrão em cada lado da estimativa.
Definição
A margem de erro para uma estatística de interesse particular é geralmente definida como o raio (ou metade da largura) do intervalo de confiança para essa estatística. O termo também pode ser usado para significar erro de amostragem em geral. Em relatos da mídia de resultados da pesquisa, o termo geralmente se refere à margem de erro máxima para qualquer porcentagem do que poll.
Margem máxima de erro
A margem de erro máxima para qualquer percentual é o raio do intervalo de confiança quando p = 50%. Como tal, pode ser calculado diretamente a partir do número de respondentes da pesquisa. Para 95% de confiança, assumindo um amostra aleatória simples a partir de uma grande população:
- Margem (máxima) de erro (95%) = 1,96 ×
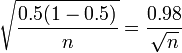
Este cálculo dá uma margem de erro de 3% para a pesquisa da Newsweek, que relatou uma margem de erro de 4%. A diferença foi provavelmente devido a ponderação ou complexas características do desenho amostral que exigiam cálculos alternativos para o erro padrão. É também possível que a Newsweek arredondados conservadora para evitar exagerar a confiança dos seus resultados.
Níveis de confiança diferentes
Para amostra aleatória simples a partir de uma grande população, a margem de erro máxima é uma re-expressão simples do tamanho da amostra n. Os numeradores dessas equações são arredondados para duas casas decimais.
- Margem de erro de 99% de confiança
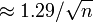
- Margem de erro de 95% de confiança
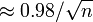
- Margem de erro de 90% de confiança
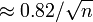
Se um artigo sobre uma pesquisa não comunica a margem de erro, mas não estado que foi usada uma simples amostra aleatória de um certo tamanho, a margem de erro pode ser calculado para um desejado grau de confiança utilizando uma das fórmulas acima. Além disso, se a margem de erro de 95% é dada, pode-se encontrar a margem de erro de 99% por aumento da margem de erro relatados por cerca de 30%.
Margens máximas e específicos de erro
Enquanto a margem de erro tipicamente relatados nos meios de comunicação é uma figura-poll ampla que reflete a variação máxima de amostragem de qualquer percentual com base em todos os inquiridos da sondagem que, a margem de erro termo também se refere ao raio do intervalo de confiança para um determinado estatística.
A margem de erro para uma percentagem indivíduo em particular será geralmente menor do que a margem de erro máxima citado para a pesquisa. Este máximo aplica-se apenas quando a percentagem observada é de 50%, e a margem de erro diminui à medida que a percentagem se aproxima dos extremos de 0% ou 100%.
Em outras palavras, a margem de erro máxima é o raio de um intervalo de confiança de 95% para uma percentagem relatada de 50%. Se p afasta-se 50%, o intervalo de confiança para p será mais curto. Deste modo, a margem de erro máxima representa um limite superior à incerteza; uma é pelo menos 95% de certeza que a percentagem "verdadeiro" está dentro da margem de erro máxima de uma percentagem relatada para qualquer percentagem relatada.
Efeito do tamanho da população
As fórmulas acima mencionadas para a margem de erro assumir que existe uma infinitamente grande população e, portanto, não depende do tamanho da população de interesse. De acordo com a teoria da amostragem , essa suposição é razoável quando a fracção de amostragem é pequena. A margem de erro para um método de amostragem em particular é essencialmente a mesma, independentemente de se a população de interesse é o tamanho de uma escola, cidade, estado, ou país, enquanto a fracção de amostragem é inferior a 10%.
Nos casos em que a fração de amostragem superior a 10%, os analistas podem ajustar a margem de erro usando "correção finita população" (FPC) para dar conta da maior precisão obtida por amostragem perto uma maior percentagem da população. FPC pode ser calculada utilizando a fórmula:
Para ajustar para uma grande fracção de amostragem, o FPC tidos em conta para o cálculo da margem de erro, que tem o efeito de diminuir a margem de erro. Ele afirma que o FPC se aproxima de zero como o tamanho da amostra (n) se aproxima do tamanho da população (N), que tem o efeito de eliminar a margem de erro inteiramente. Isso faz sentido intuitivo porque quando N = n, a amostra torna-se um censo e erro de amostragem torna-se discutível.
Analistas deve estar consciente de que a amostra permanecer verdadeiramente aleatório como a fracção de amostragem cresce, para que não viés de amostragem ser introduzido.
Outras estatísticas
Intervalos de confiança podem ser calculados, e por isso pode margens de erro, para uma série de estatísticas, incluindo percentagens individuais, diferenças entre porcentagens, médias, medianas e totais.
A margem de erro para a diferença entre as duas percentagens é maior do que as margens de erro para cada uma destas percentagens, e pode mesmo ser maior do que a margem de erro máxima para qualquer indivíduo percentagem do levantamento.
Comparando percentuais
Em um sistema de votação pluralidade, é importante saber quem está à frente. Os termos "empate técnico" e "empate técnico" às vezes são usados para descrever percentagens reportadas que diferem por menos de uma margem de erro, mas estes termos podem ser enganadores. Por um lado, a margem de erro calculada como geralmente se aplica a um percentual individual e não a diferença entre as percentagens, por isso a diferença entre duas estimativas percentuais podem não ser estatisticamente significativo, mesmo quando eles diferem em mais do que a margem de erro relatados. Os resultados da pesquisa também muitas vezes fornecem informações forte, mesmo quando não há uma diferença estatisticamente significativa.
Quando se comparam as percentagens, pode por conseguinte ser útil considerar a probabilidade de que uma percentagem superior de outra. Em situações simples, essa probabilidade pode ser derivada com 1) o cálculo de erro padrão introduzido no início, 2) a fórmula para a variância da diferença de duas variáveis aleatórias , e 3) um pressuposto de que, se alguém não escolher Kerry eles vão escolher de Bush , e vice-versa; eles são perfeitamente negativamente correlacionados . Isto pode não ser uma suposição defensável quando existem mais de duas possíveis respostas da consulta. Para mais projetos de pesquisa complexas, devem ser usados diferentes fórmulas para o cálculo do erro padrão da diferença.
O erro padrão da diferença de percentagens p para Kerry e q para Bush, assumindo que eles estão perfeitamente correlacionados negativamente, a seguir:
- Erro padrão da diferença =
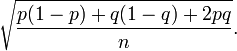
Dada a diferença percentual observado P - Q (2% ou 0,02) e o erro padrão da diferença calculada acima (0,03), qualquer calculadora estatística podem ser usadas para calcular a probabilidade de que uma amostra de uma distribuição normal com média de 0,02 e padrão desvio de 0,03 é maior que 0.
Aplicando estes cálculos para os resultados de exemplo Newsweek em uma probabilidade de 75% que Kerry era "verdadeiramente" líder.