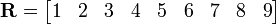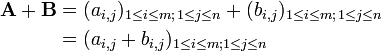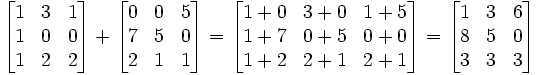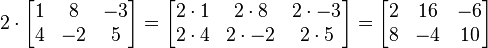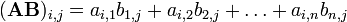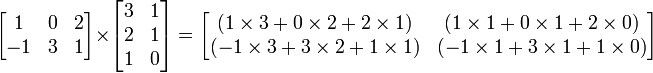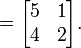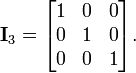Matrix (matemática)

Assuntos Relacionados: Matemática

Fundo para as escolas Wikipédia

Crianças SOS tentou tornar o conteúdo mais acessível Wikipedia por esta selecção escolas. Antes de decidir sobre o patrocínio de uma criança, por que não aprender sobre as diferentes instituições de caridade de patrocínio primeiro ?

Em matemática , uma matriz (matrizes plural) é uma mesa rectangular de elementos (ou entradas), que podem ser números ou, mais geralmente, qualquer quantidades abstratas que podem ser adicionados e se multiplicava. Matrizes são usadas para descrever equações lineares , acompanhar o coeficientes de transformações lineares e para registrar os dados que dependem de vários parâmetros. As matrizes são descritas pelo campo da teoria da matriz . As matrizes podem ser adicionados, multiplicaram-se, e decomposto em várias maneiras, o que também os torna um conceito-chave no campo da álgebra linear .

Neste artigo, as entradas de uma matriz são reais ou complexos números salvo indicação em contrário.

Organização de uma matriz

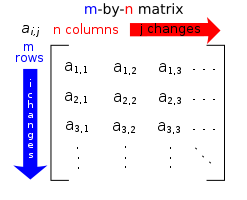
Definições e notações

As linhas horizontais em uma matriz são chamados de linhas e as linhas verticais são chamadas colunas. Uma matriz com m linhas e n colunas é chamado um m n -by- matriz (escrito m x n) e m e n são chamados as suas dimensões. As dimensões de uma matriz são sempre indicadas com o número de linhas em primeiro lugar, então o número de colunas. É comumente dito que uma matriz -by- n m tem uma ordem de m × n ("ordem" significa tamanho). Duas matrizes de mesma ordem cujas entradas correspondentes são equivalentes são considerados iguais.

Quase sempre letras maiúsculas denotam matrizes com as correspondentes letras minúsculas com dois índices que representam as entradas. Por exemplo, a entrada de uma matriz A que se encontra na linha i-ésimo e o j -ésimo coluna está escrito como uma _{i, j} e chamado o i, a entrada j ou (i, j) -ésimo entrada de A. Notações alternativas para que a entrada é a [i, j] ou A _{i, j.} A linha é sempre observado pela primeira vez, em seguida a coluna. Neste exemplo, A (sem subscritos) que simbolizam toda a matriz. Além de usar letras maiúsculas como símbolos que representam matrizes, muitos autores usam um estilo tipográfico especial, comumente negrito na posição vertical (não itálico), para distinguir ainda mais matrizes de outras variáveis. Seguindo esta convenção, A é uma matriz, que se distingue de A, um escalar. Uma convenção alternativo é para anotar matrizes com as suas dimensões em letras pequenas por baixo do símbolo, por exemplo, 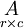$\ ressaca {r \ times c} {A}$ por uma matriz de c r -by-.

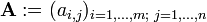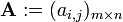Nós muitas vezes escrever $\ Mathbf {A}: = (a_ {i, j}) _ {i = 1, \ ldots, m; \, \, j = 1, \ ldots, n}$ ou $\ Mathbf {A}: = (a_ {i, j}) _ {m \ times n}$ para definir uma matriz m x n A. Neste caso, as entradas de um _{i, j} são definidos separadamente para todos os números inteiros 1 ≤ i ≤ M e 1 ≤ j ≤ n. Em algumas linguagens de programação, a numeração de linhas e colunas começa em zero. Textos que usam tal linguagem extensivamente, freqüentemente siga essa convenção, por isso temos 0 ≤ i ≤ m -1 e 0 ≤ j ≤ n -1.

Uma matriz em que uma das dimensões é igual a um é frequentemente chamado de vector, e interpretada como um elemento de espaço real de coordenadas . Uma matriz m × 1 (uma coluna e linhas m) é chamado de vector de coluna e uma matriz n 1 × (uma linha e n colunas) é chamado um vetor linha.

Definição matemática

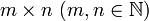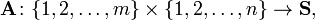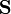Um $\, M \ times n \, \, (m, n \ in \ mathbb {N})$ matriz $\ Mathbf {A} \,$ é uma função $\ Mathbf {A} \ cólon \ {1, 2, \ ldots, m \} \ times \ {1, 2, \ ldots, n \} \ a \ mathbf {S}, \, \,$ onde $\ Mathbf {S} \,$ é qualquer não- conjunto vazio.

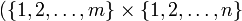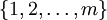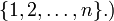
$(\ {1, 2, \ ldots, m \} \ times \ {1, 2, \ ldots, n \} \,$ é o Produto cartesiano de conjuntos $\ {1, 2, \ ldots, m \} \,$ e $\ {1, 2, \ ldots, n \}.) \,$

Nós dizemos que a matriz 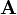$\ Mathbf {A}$ é uma matriz sobre o conjunto 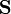$\ Mathbf {S}$ . Algo importante para notar é que, se queremos ter álgebra matricial, o conjunto 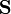$\ Mathbf {S} \,$ deve ser um anel e matriz 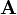$\ Mathbf {A}$ deve ser uma matriz quadrada (ver matrizes quadrados e definições relacionadas abaixo para mais explicações). Uma vez que o conjunto de todas as matrizes quadradas ao longo de um anel é também um anel, álgebra de matrizes é chamado geralmente anel matriz.

Desde que este artigo considera principalmente matrizes sobre números reais , as matrizes mostradas aqui são realmente funções 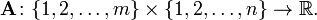$\ Mathbf {A} \ cólon \ {1, 2, \ ldots, m \} \ times \ {1, 2, \ ldots, n \} \ to \ mathbb {R}. \, \,$

Exemplo

A matriz

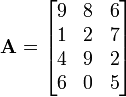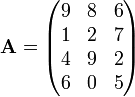
$\ Mathbf {A} = \ begin {} bmatrix 9 & 8 & 6 \\ 1 & 2 & 7 \\ 4 e 9 & 2 & 6 \\ 0 & 5 \ end {bmatrix}$ ou $\ Mathbf {A} = \ begin {} pmatrix 9 & 8 & 6 \\ 1 & 2 & 7 \\ 4 e 9 & 2 & 6 \\ 0 & 5 \ end {pmatrix}$

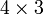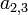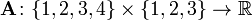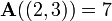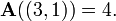
é um $4 \ times 3$ matriz. O elemento $a_ {2,3}$ ou $\ Mathbf {A} [2,3]$ é 7. Em termos de a definição matemática dada acima, esta matriz é uma função $\ Mathbf {A} \ cólon \ {1, 2, 3, 4 \} \ times \ {1, 2, 3 \} \ to \ mathbb {R} \,$ e, por exemplo, $\ Mathbf {A} ((2, 3)) = 7 \,$ e $\ Mathbf {A} ((3, 1)) = 4. \,$

A matriz

$\ Mathbf {R} = \ begin {} bmatrix 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 e 9 \ end {bmatrix}$

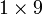é um $1 \ 9 vezes$ matriz, ou 9-elemento de linha vector.

Adição e multiplicação de matrizes

Soma

Dois ou mais matrizes de dimensões idênticas M e N podem ser adicionados. M -by- n matrizes Dado A e B, a sua soma A + B é a matriz de m -by- n calculado pela adição de elementos correspondentes:

$\ Begin {align} \ mathbf {A} + \ mathbf {B} & = (a_ {i, j}) _ {1 \ le i \ m le; \, 1 \ le j \ le n} + (b_ { i, j}) _ {1 \ le i \ m le; \, 1 \ le j \ le n} \\ & = (a_ {i, j} + b_ {i, j}) _ {1 \ le i \ m le; 1 \ le j \ le n} \\ \ end {align}$

Por exemplo:

$\ Begin {} bmatrix 1 & 3 & 1 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \ end {bmatrix} + \ begin {bmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \ end {bmatrix} = \ begin {} bmatrix 1 + 0 e 3 + 0 e 1 + 1 + 5 \\ 7 e 0 + 5 e 0 + 0 \\ 1 + 2 e 2 + 1 & 2 1 \ end {bmatrix} = \ begin {} bmatrix 1 & 3 & 6 \\ 8 & 5 & 0 \\ 3 & 3 & 3 \ end {bmatrix}$

Outra noção, muito usado com menos frequência de adição de matriz é o soma direta.

Multiplicação escalar

Dada uma matriz A e um número de C, o c multiplicação escalar A é calculado multiplicando-se a cada elemento de uma pela escalar C (ou seja 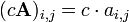$(C \ mathbf {A}) _ {i, j} = c \ cdot a_ {i, j}$ ). Por exemplo:

$2 \ cdot \ begin {} bmatrix 1 e 8 e -3 \\ 4 & 5 & -2 \ end {bmatrix} = \ begin {} bmatrix 2 \ cdot 1 & 2 \ cdot 8 e 2 \ cdot -3 \\ 2 \ cdot 4 & 2 \ cdot -2 e 2 \ cdot 5 \ end {bmatrix} = \ begin {} bmatrix 2 & 16 & -6 \\ 8 e -4 e 10 \ end {bmatrix}$

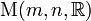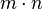Além Matrix e multiplicação escalar transformar o conjunto $\ Texto {H} (m, n, \ mathbb {R})$ de tudo $m$ -by- $n$ matrizes com reais entradas para um verdadeiro espaço vetorial de dimensão $m \ cdot n$ .

A multiplicação de matrizes

A multiplicação de matrizes é dois bem definido apenas se o número de colunas da matriz esquerda é o mesmo que o número de linhas da matriz direita. O ponto médio ( $\ Cdot$ ) Não é usado para indicar a multiplicação de matrizes (que é usado para a multiplicação escalar). Se A é uma matriz m -by- N e B é um N -by- p matriz, em seguida, o seu produto de matrizes AB é o m p -by- matriz dada por:

$(\ Mathbf {AB}) _ {i, j} = {i a_, b_ 1} {1, j} + a_ {i, 2} b_ {2, j} + \ ldots + a_ {i, n} b_ {n, j}$

para cada par 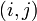$(I, j)$ . Por exemplo:

$\ Begin {} bmatrix 1 & 2 0 e -1 \\ & 3 & 1 \\ \ end {bmatrix} \ times \ begin {} bmatrix 3 & 1 & 2 \\ 1 \\ 1 & 0 \\ \ end { bmatrix} = \ begin {} bmatrix (1 \ times 3 + 0 \ times 2 + 2 \ times 1) e (1 \ times 1 + 0 \ times 1 + 2 \ times 0) \\ (-1 \ times 3 + 3 \ times 2 + 1 \ times 1) e (-1 \ vezes 1 + 3 \ times 1 + 1 \ times 0) \\ \ end {bmatrix}$

$= \ Begin {} bmatrix 5 & 1 & 2 4 \\ \\ \ end {} bmatrix.$

A multiplicação de matrizes tem as seguintes propriedades:

(AB) C = A (BC) para todo k -by- m matrizes A, m -by- n matrizes B e n -by- p matrizes C ("associatividade").
(A + B): C = AC + CB para todos m -by- n matrizes A e B e n -by- k matrizes C ("distribuitivamente direita").
C (A + B) = CA + CB para todos m -by- n matrizes A e B e K -by- m matrizes C ("esquerda distribuitivamente").

A multiplicação de matrizes não é comutativa ; que é, tendo em conta as matrizes A e B e o seu produto definido, em seguida, geralmente AB 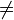$\ Ne$ BA. Também pode acontecer que AB é definido mas BA não está definido.

Além da multiplicação de matrizes comum que acabamos de descrever, existem outras operações em matrizes que podem ser consideradas formas de multiplicação, tais como o produto de Hadamard e o Produto de Kronecker.

Transformações lineares, classifica e transpor

As matrizes podem representar convenientemente transformações lineares porque a multiplicação de matrizes perfeitamente correspondente à composição de mapas, tal como será descrito a seguir. Esta mesma propriedade torna estruturas de dados poderosos em linguagens de programação de alto nível.

Aqui e na sequela identificamos R ⁿ com o conjunto de "colunas" ou n -por-1 matrizes. Para cada mapa linear f: R ⁿ → R ^m existe uma única m -by- n matriz A tal que f (x) = Ax para todo x em R ^n. Dizemos que a matriz A "representa" o mapa linear f. Agora, se o k -by- m matriz B representa mais um mapa linear g: R → R ^{m k,} então o mapa linear g o f é representado pela BA. Isso decorre da associatividade da multiplicação matriz acima mencionado.

Mais geralmente, um mapa linear de um espaço n-dimensional a um vector de m de espaço vectorial -dimensional é representado por uma matriz m -by- n, desde que bases foram escolhidos para cada.

O posto de uma matriz A é o dimensão do imagem do mapa linear representado por A; esta é a mesma que a dimensão do espaço gerado pelas linhas de A, e também a mesma que a dimensão do espaço gerado pelas colunas de A. Também pode ser definido sem referência a álgebra linear como se segue: a patente de uma matriz n m -by- A é menor o número k tal que A pode ser escrito como um produto BC em que B é uma matriz -by- m e k C é uma matriz n k -by- (embora isto não é um modo prático para calcular o grau).

O transposição de uma matriz n m -by- A é o n -by- m matriz A ^{de tr} (também por vezes escrito como um ^t ou ^t A) formado por transformar linhas em colunas e linhas em colunas, ou seja ^a Tr [i, j] = A [j, i] para todos os índices i e j. Se A descreve um mapa linear em relação a duas bases, em seguida, a matriz A ^tr descreve a transposta do mapa linear em relação às bases duplas, ver espaço dual.

Temos (A + B) ^{tr tr} = A + B e ^tr (AB) = B ^{tr tr tr} A.

Matrizes quadradas e definições relacionadas

A matriz é uma matriz quadrada que tem o mesmo número de linhas e colunas. O conjunto de todos os quadrados n -by- n matrizes, juntamente com a adição e multiplicação de matrizes é um anel. A menos que n = 1, este anel não é comutativa .

M (n, R), o anel de reais matrizes quadradas, é um verdadeiro unitário álgebra associativa. M (n, C), o anel de matrizes quadradas complexas, é uma álgebra associativa complexo.

A matriz ou unidade matriz identidade I _n, com elementos na diagonal principal set a 1 e todos os outros elementos fixados a 0, satisfaz MI _n = M e eu _{n N} = N para qualquer m -by- n matriz M e n -by- k matriz N. Por exemplo, se n = 3:

$\ Mathbf {I} _3 = \ begin {} bmatrix 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {} bmatrix.$

A matriz de identidade é o elemento identidade no anel de matrizes quadradas.

Elementos invertíveis neste anel são chamados matrizes invertíveis ou matrizes não-singulares. Um n pela matriz n A é invertível se, e somente se existir uma matriz B de tal forma que

AB = I _n (= BA).

Neste caso, B é a matriz inversa de A, designada por ^A-1. O conjunto de todos invertíveis n -by- n matrizes forma um grupo (especificamente uma Grupo de Lie), sob a multiplicação de matrizes, o grupo linear geral.

Se λ é um número e v é um vetor não nulo tal que Av = λ v, então nós chamamos v um autovetor de A e λ o associado valor próprio . (Eigen significa "possuir" em alemão e em holandês ). O número λ é um autovalor de A se e somente se A -λ Eu _n não é invertida, o que acontece se, e somente se p _A (λ) = 0. Aqui p _A (x) é a polinomial característica de um. Este é um polinômio de grau n e tem, portanto, n raízes complexas (contando múltiplas raízes de acordo com a sua multiplicidade). Neste sentido, cada matriz quadrada tem valores próprios complexos n.

O determinante de uma matriz quadrada A é o produto dos seus n valores próprios, mas também pode ser definida pela Fórmula Leibniz. Matrizes invertíveis são precisamente essas matrizes com um determinante diferente de zero.

A eliminação de Gauss algoritmo é de importância central: ele pode ser usado para calcular determinantes, fileiras e inversas de matrizes e para resolver sistemas de equações lineares .

O traço de uma matriz quadrada é a soma de suas entradas diagonais, o que equivale a soma de seus valores próprios n.

Matrix exponencial é definida para matrizes quadradas, usando séries de potências .

Tipos especiais de matrizes

Em muitas áreas da matemática, matrizes com certa estrutura surgir. Alguns exemplos são importantes

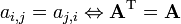Matrizes simétricas são tais que elementos simétricos com relação a diagonal principal (a partir do canto superior esquerdo para o canto inferior direito) são iguais, isto é, $A_ {i, j} = a_ {j, i} \ Leftrightarrow \ mathbf {A} ^ \ mathrm {T} = \ mathbf {A}$ .
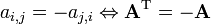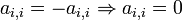Enviesar-simétrica matrizes são tais que os elementos simétricos sobre a diagonal principal é o negativo um do outro, isto é, $a_ {i, j} = - a_ {j, i} \ Leftrightarrow \ mathbf {A} ^ \ mathrm {T} = - \ mathbf {A}$ . Em uma Matriz Antissimétrica, todos os elementos da diagonal são iguais a zero, isto é, $a_ {i, i} = - a_ {i, i} \ Rightarrow a_ {i, i = 0}$ .
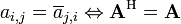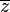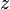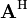Hermitianas (ou auto-adjuntas) matrizes são tais que elementos simétricos com relação a diagonal são cada outro Os conjugados complexos, isto é, $a_ {i, j} = \ overline {a} _ {j, i} \ Leftrightarrow \ mathbf {A} ^ \ mathrm {H} = \ mathbf {A}$ , Onde $\ Overline {z}$ significa o complexo conjugado de um número complexo $z$ e $\, \! \ Mathbf {A} ^ \ mathrm {H}$ o conjugado transposta de uma.
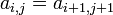Matrizes de Toeplitz têm elementos comuns em suas diagonais, isto é, $\, \! A_ {i, j} = a_ {i + 1, j + 1}$ .
Matrizes estocásticos são matrizes quadradas cujas linhas são vetores de probabilidade; eles são utilizados para definir Cadeias de Markov.
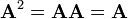Uma matriz quadrada A é chamado idempotent se $\ Mathbf {A} ^ 2 = \ mathbf {AA} = \ mathbf {A}$ .

Para obter uma lista mais extensa ver lista de matrizes.

Matrizes em álgebra abstrata

Se começarmos com um anel R, pode-se considerar o conjunto M (m, n, R) de todos os m por n matrizes com entradas em R. A adição e a multiplicação de matrizes estas podem ser definidas como no caso das matrizes reais ou complexos (ver acima ). O conjunto M (n, R) de todos n quadrado por n matrizes mais de R é um anel em seu próprio direito, isomorfo ao anel endomorphism da esquerda R - módulo R ^n.

Da mesma forma, se as entradas forem tomadas a partir de um semianel S, adição e multiplicação de matriz pode ainda ser definida como de costume. O conjunto de todos os n praça × n matrizes mais de S é em si um semianel. Observe que a matriz rápido algoritmos de multiplicação, como o Strassen algoritmo geralmente só se aplica a matrizes sobre os anéis e não vai funcionar para matrizes sobre semirings que não são anéis.

Se R é um anel conmutativo , então M (n, R) é um unitária álgebra associativa mais de R. Em seguida, é também significativo para definir o determinante de matrizes quadradas usando o Leibniz fórmula; uma matriz é inversível se e somente se seu determinante é invertida em R.

Todas as declarações mencionadas neste artigo para matrizes de reais ou complexos permanecer correto para matrizes sobre um arbitrária campo.

Matrizes mais de um anel de polinômios são importantes no estudo da teoria de controle .

Matrizes sem entradas

Uma pergunta sutil que quase nunca é colocada é se existe tal coisa como uma matriz de 3 por 0. Isso seria uma matriz com três linhas mas sem nenhuma coluna, o que parece absurdo. No entanto, se alguém quiser ser capaz de ter matrizes para todos os mapas lineares entre espaços vetoriais de dimensão finita, é preciso tais matrizes, uma vez que não há nada de errado com mapas lineares de um espaço de 0-dimensional para um espaço 3-dimensional (na verdade, se os espaços são fixados existe um tal mapa, o mapa zero). Assim, somos levados a admitir que há exatamente um 3-por-0 da matriz (que tem 3 × 0 = 0; entradas entradas não nulas, mas nenhum). Da mesma forma, existem matrizes com um número positivo de colunas, mas não há linhas. Além disso, mesmo na ausência de entradas, um deve ainda manter um registo do número de linhas e colunas, desde que o produto BC em que B é a matriz de 3 por 0 e C é uma matriz 0-por-4 é um perfeitamente normal 3 -por-4 matriz, cuja totalidade das 12 entradas são de 0 (como são dadas por uma soma vazia). Note-se que este cálculo do BC justifica o critério dado acima para o posto de uma matriz em termos de possíveis expressões como um produto: a matriz 3-por-4 com zero entradas certamente tem posto 0, por isso deve ser o produto de um 3 -by-0 matriz e uma matriz 0-por-4. Para permitir distinguir entre matrizes e sem entradas, matrizes deve ser formalmente definida, em um estilo de ciência da computação um tanto pedante, como quadruplica (A, r, c, M), onde A é o conjunto no qual as entradas ao vivo, R e C são os números (naturais) de linhas e colunas, e M é o conjunto rectangular de elementos RC de A (a matriz no sentido usual).

História

O estudo de matrizes é bastante antiga. A 3-por-3 quadrado mágico aparece em Chinês literatura namoro já a partir de 650 aC.

Matrizes têm uma longa história de aplicação na resolução de equações lineares . Um importante Texto em chinês de entre 300 aC e 200 dC, Os Nove Capítulos da Arte Matemática (Jiu Zhang Suan Shu), é o primeiro exemplo do uso de métodos matriciais para resolver equações simultâneas . No sétimo capítulo, "Too much e não o suficiente", o conceito de um determinante aparece pela primeira vez há quase 2000 anos antes de sua publicação pela Matemático japonês Seki Kowa em 1683 e matemático alemão Gottfried Leibniz em 1693.

Quadrados mágicos eram conhecidos Matemáticos árabes, possivelmente tão cedo quanto o século 7, quando os árabes conquistaram partes do noroeste do Subcontinente indiano e aprendeu matemática indiana e astronomia, incluindo outros aspectos da matemática combinatória . Também tem sido sugerido que a ideia veio através da China. Os primeiros quadrados mágicos de ordem 5 e 6 de aparecer em uma enciclopédia de Bagdá circa 983 dC, o Enciclopédia dos Irmãos da Pureza (Rasa'il Ihkwan al-Safa); mais simples quadrados mágicos eram conhecidos por vários matemáticos árabes anteriores.

Após o desenvolvimento da teoria de determinantes por Seki Kowa e Leibniz no final do século 17, Cramer desenvolveu a teoria ainda mais no século 18, apresentando Regra de Cramer em 1750 . Carl Friedrich Gauss e Wilhelm Jordan desenvolvido Eliminação de Gauss-Jordan em 1800.

O termo "matriz" foi cunhado em 1848 por JJ Sylvester. Cayley, Hamilton, Grassmann, Frobenius e von Neumann estão entre os famosos matemáticos que trabalharam na teoria da matriz.

Olga Taussky-Todd (1906-1995) fez importantes contribuições à teoria de matriz, usando-o para investigar um fenômeno chamado de aerodinâmica esvoaçantes ou aeroelasticidade durante a Segunda Guerra Mundial . Ela tem sido chamado de "um portador da tocha" para a teoria matriz.

Educação

Matrizes foram tradicionalmente ensinada como parte de álgebra linear na faculdade, ou com cálculo. Com a adoção do textos de matemática integrado para uso na escola na década de 1990, eles foram incluídos por muitos textos tais como a Núcleo-Plus Projeto Matemática, que são muitas vezes alvo tão cedo quanto o nono ano, ou mais cedo para as honras alunos. Eles muitas vezes requerem o uso de calculadoras gráficas, tais como o TI-83, que pode executar operações complexas, tais como inversão de matriz muito rapidamente.

Embora a maioria das linguagens de computador não são projetados com comandos ou bibliotecas para matrizes, no início dos anos 1970, alguns computadores desktop de engenharia, tais como o HP 9830 teve cartuchos ROM para adicionar comandos básicos para matrizes. Algumas linguagens de computador, tais como APL, foram projetados para manipular matrizes e programas matemáticos tais como Mathematica, juntamente com De bordo, Matlab, e Oitava também são utilizados para auxiliar a computação com matrizes.

Aplicações

Encryption

As matrizes podem ser usadas para encriptar dados numéricos. Criptografia é feito através da multiplicação da matriz de dados com uma matriz de teclado. A descriptografia é feita simplesmente através da multiplicação da matriz encriptada com o inverso da chave.

Gráficos de computador

4 × 4 matrizes de transformação são comumente usados em computação gráfica. A esquerda 3 × 3 porção superior de uma matriz de transformação é composto pelo novo X, Y, e Z. do pós-transformação das coordenadas de espaço.

Retirado de " http://en.wikipedia.org/w/index.php?title=Matrix_(mathematics)&oldid=199124713 "

We provide Linux to the World