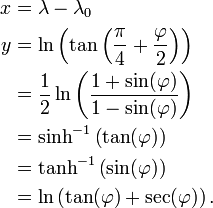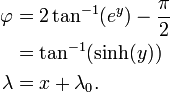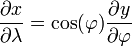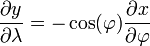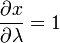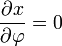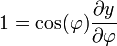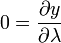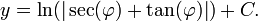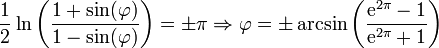Projeção Mercator

Mercator mapa Nova et Orbis Terrae Aucta Descriptio anúncio Usum Navigatium emendate (1569)

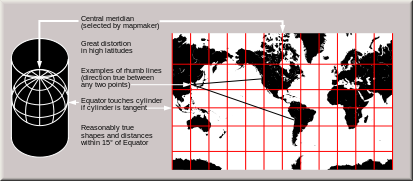
A projeção Mercator é uma projeção cilíndrica mapa apresentado pela Geógrafo e cartógrafo Flamengo Gerardus Mercator, em 1569. Tornou-se o mapa de projeção padrão para fins náuticos devido à sua capacidade para representar linhas de constante rolamento verdadeiro ou verdadeiro claro, conhecidos como linhas de rumo, como em linha reta segmentos de linha. Enquanto a direção e formas são precisos em uma projeção Mercator, distorce tamanho, em um grau crescente de distância do equador.

Propriedades e detalhes históricos

A edição de 1569 Mercator era um grande planisfério medindo 202 por 124 cm, impressas em dezoito folhas separadas. Como em todas as projecções cilíndricas , paralelos e meridianos estão direitas e perpendiculares um ao outro. Ao realizar isso, o inevitável leste-oeste que se estende do mapa, o que aumenta a distância das equador aumenta, é acompanhada por um correspondente sul-norte que se estende, de modo que em cada local de ponto, a escala leste-oeste é o mesmo que a escala norte-sul, fazendo a projecção conformado. Um mapa Mercator nunca pode mostrar plenamente as áreas polares, desde escala linear torna-se infinitamente alta nos pólos. Sendo uma projeção conforme, os ângulos são preservados em torno de todos os locais, no entanto escala varia de lugar para lugar, distorcendo o tamanho dos objetos geográficos. Em particular, as áreas mais estreitas para os pólos são mais afectadas, a transmissão de uma imagem da geometria do planeta que é mais falseada o mais perto dos postes. Em latitudes superiores a 70 ° norte ou sul, a projeção Mercator é praticamente inutilizável.

A mapa estelar com projeção cilíndrica semelhante à projeção Mercator, a partir do livro de Xin Yi Xiang o Fa Yao, publicado em 1092 pelo chinês cientista Su Song.

Todas as linhas de constante rolamento ( linhas de rumo ou loxodromes - aqueles que fazem ângulos constantes com os meridianos), são representados por segmentos retos em um mapa Mercator. Este é precisamente o tipo de rota geralmente empregada por navios no mar, onde compassos são usados para indicar direções geográficas e para orientar os navios. As duas propriedades, conformalidade e em linha reta linhas de rumo, fazer essa projeção exclusivamente adequado para a navegação marítima: cursos e rolamentos são medidos utilizando-vento rosas ou transferidores, e as direcções correspondentes são facilmente transferidos de ponto a ponto, no mapa, com a ajuda de um régua paralelo ou um par de praças de navegação.

O nome e as explicações dadas por Mercator para o seu mapa do mundo (ad Nova et Orbis Terrae Aucta Descriptio Usum Navigatium emendate: "descrição nova e aumentada da Terra corrigido para a utilização da navegação") mostram que foi expressamente concebido para a utilização da navegação marítima . Embora o método de construção não é explicado pelo autor, Mercator provavelmente utilizado um método gráfico, a transferência de algumas linhas de rumo previamente traçados em um globo para uma praça retícula, e, em seguida, ajustar o espaçamento entre os paralelos de modo a que as linhas se tornou linear, fazendo o mesmo ângulo com os meridianos como no globo.

O desenvolvimento da projeção Mercator representou um grande avanço na cartografia náutica do século 16. No entanto, foi muito à frente de seu tempo, uma vez que as velhas técnicas de navegação e levantamento topográfico não eram compatíveis com a sua utilização na navegação. Dois problemas principais impediram a sua aplicação imediata: a impossibilidade de determinar a longitude no mar com uma precisão adequada e com o fato de que instruções magnéticos, em vez de instruções geográficas, foram usadas na navegação. Apenas no meio do século 18, após o cronómetro marinho foi inventado e da distribuição espacial da declinação magnética era conhecido, poderia a projeção Mercator ser plenamente adotada pelos navegadores.

Vários autores estão associados com o desenvolvimento de projecção Mercator:

• Alemão Erhard Etzlaub (c. 1460-1532), que tinha gravado em miniatura "mapas de compasso" (cerca de 10x8 cm) da Europa e partes da África, latitudes 67 ° -0 °, para permitir o ajuste de seus relógios de bolso portáteis, foi para décadas declarou ter concebido "uma projeção Mercator idêntico ao do". Este, desde então, provou ser um erro, remontando à pesquisa doubtable em 1917.

• Matemático e cosmógrafo português Pedro Nunes (1502-1578), que primeiro descreveu a loxodrome e seu uso na navegação marítima, e sugeriu a construção de várias cartas náuticas de grande escala na projeção equidistante cilíndrica para representar o mundo com o mínimo de distorção ângulo (1537).

• Inglês matemático Edward Wright (c. 1558-1615), que formalizou a matemática da projeção Mercator (1599), e publicou tabelas precisas para a sua construção (1599, 1610).

• Matemáticos ingleses Thomas Harriot (1560-1621) e Henry Bond (c.1600-1678), que, de forma independente (c. 1600 e 1645), associado a projeção Mercator com sua fórmula logarítmica moderna, mais tarde deduzido por cálculo.

Matemática da projecção

Relação entre a posição vertical, sobre o mapa (horizontal no gráfico) e latitude (vertical no gráfico).

As seguintes equações determinar a x e y coordenadas de um apontar em um mapa Mercator de sua latitude φ e λ longitude (λ com ₀ sendo a longitude no centro do mapa):

Isto é o inverso do Função Gudermannian:

Isto é o Função Gudermannian:

A escala é proporcional à secante da latitude φ, ficando arbitrariamente grande perto do pólos, onde φ = ± 90 °. Além disso, como pode ser visto a partir das fórmulas, do pólo y é infinito mais ou para menos.

Derivação da projeção

A projeção Mercator é uma projeção cilíndrica.

Suponha uma Terra esférica. (É realmente ligeiramente achatado, mas para pequena escala mapeia a diferença é irrelevante. Para obter mais precisão, interpor conformada latitude .) Procuramos uma transformação de longitude-latitude (λ, φ) para cartesiano (x, y) que é "um cilindro tangente ao equador" (ie x = λ) e conformado, de modo que :

A partir de x = λ chegarmos

dando

Assim y é uma função somente de φ com 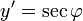a partir do qual um tabela de integrais dá

É conveniente para mapear φ = 0 para y = 0, assim que tomar C = 0.

Usos

Indicatriz de Tissot

O acima reprojectado como sinusoidal

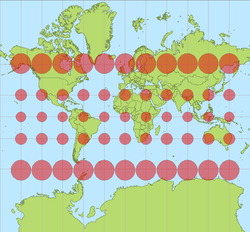
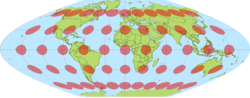
Como todas as projecções mapa que tentam encaixar uma superfície curva sobre uma folha plana, a forma do mapa é uma distorção do verdadeiro disposição da superfície da Terra. A projeção Mercator exagera o tamanho das áreas longe do equador . Por exemplo:

• Greenland é apresentado como tendo área de terra mais ou menos tanto quanto a África , quando na verdade a área da África é aproximadamente 14 vezes maior do que a Groenlândia.
• Alaska é apresentado como tendo semelhante ou até um pouco mais área de terra do que Brasil , quando a área do Brasil é, na verdade, mais de 5 vezes maior do que o Alasca.
• Finlândia é apresentado como tendo uma maior extensão Norte-Sul como a Índia , quando essa distância é muito maior na Índia do que na Finlândia.

Embora a projeção Mercator ainda está em uso comum para a navegação, devido às suas propriedades únicas, cartógrafos concorda que não é adequado para representar todo o mundo em publicações ou mapas de parede, devido à sua distorção da área de terra. Mercator-se usado a-área igual projeção senoidal para mostrar áreas relativas. Como resultado destas críticas, moderno atlas já não usam a projeção Mercator para mapas do mundo ou para áreas distantes do equador, preferindo outras projecções cilíndricas , ou formas de projeção em área igual . A projeção Mercator ainda é comumente usado para áreas perto do equador, no entanto, onde a distorção é mínima.

Arno Peters provocou polêmica quando propôs o que é conhecido como a projeção Gall-Peters , uma ligeira modificação da projeção Lambert Equal-cilíndricos Area, como a alternativa para a Mercator. A resolução 1989 por sete grupos geográficos norte-americanos criticaram a utilização de todos os mapas do mundo retangulares de coordenadas, incluindo o Mercator e Gall-Peters.

Google Maps atualmente usa uma projeção Mercator para suas imagens de mapa. Apesar de suas distorções escala relativa, a Mercator é bem adequada como um mapa interativo que pode ser deslocada e ampliada de forma transparente para mapas locais. (Google Maps por Satélite, por outro lado, usou um projeção placa carrée até 2005-07-22 .)

O Google Maps φ máxima latitude ocorre em ± 85,05113 graus quando as Mercator y = valor de π. Ou mais precisamente: