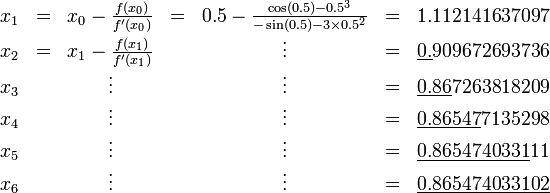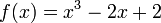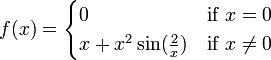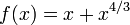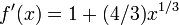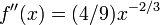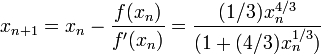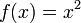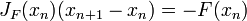O método de Newton

Em análise numérica, o método de Newton (também conhecido como o Newton- Raphson ou o método de Newton-Fourier) é talvez o método mais conhecido para encontrar melhores aproximações, sucessivamente, para os zeros (ou raízes) de uma verdadeira -valued função . O método de Newton pode muitas vezes convergem com uma rapidez impressionante, especialmente se a iteração começa a raiz "suficientemente próximo" desejado. Quão perto "suficientemente próximo" precisa ser e quão rapidamente "com uma rapidez impressionante" pode ser depende do problema, como é discutido em detalhe abaixo. Infelizmente, longe da raiz desejado, o método de Newton pode facilmente levar um usuário incauto desviado e perdido com pouco aviso. Assim, as boas implementações do método incorporá-lo em uma rotina que também detecta e talvez supera possíveis falhas de convergência.

O método de Newton, também pode ser usada para encontrar um mínimo ou máximo de uma tal função, por encontrar um zero na primeira derivada da função, ver O método de Newton como um algoritmo de optimização.

O algoritmo é o primeiro na classe de Métodos de chefe de família, sucedido por O método de Halley.

Descrição do método de

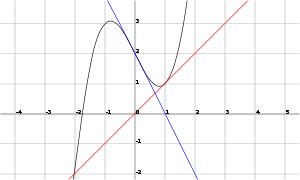
A ideia de que o método é como se segue: começa-se com uma estimativa inicial que é razoavelmente perto da raiz verdadeiro, então a função é aproximada pela sua linha tangente (que pode ser calculada usando as ferramentas de cálculo ), e um computa o x -intercept desta linha tangente (que é facilmente feito com álgebra elementar). Este x -intercept será tipicamente uma melhor aproximação para a raiz da função do que a estimativa inicial, e o método pode ser iterado.

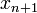Uma ilustração de uma iteração do método de Newton (a função F é mostrado em azul e a linha tangente é a vermelho). Vemos que é uma aproximação melhor do que 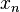para a raiz 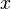da função .

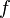Suponha f: [a, b] → R é um diferenciável função definida na intervalo [a, b] com valores no números reais R. A fórmula para convergir para a raiz pode ser facilmente derivada. Suponha que temos alguns dos actuais aproximação x _n. Então, podemos derivar a fórmula para uma melhor aproximação, x _{n + 1,} referindo-se o diagrama à direita. Sabemos da definição do derivado num dado ponto que é o declive da tangente a esse ponto.

Isto é

.

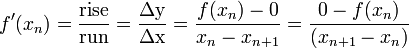Aqui, f 'indica o derivado da função f. Então por álgebra simples podemos derivar

.

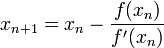Começamos o processo com algum valor inicial arbitrário x _0. (Quanto mais próximo do zero, melhor. Mas, na ausência de qualquer intuição sobre onde o zero poderia mentir, um "palpite e verificar" método pode limitar as possibilidades para um intervalo razoavelmente pequeno, apelando para o teorema do valor intermediário.) O método geralmente irão convergir, desde que esta estimativa inicial é perto o suficiente para zero desconhecido, e que 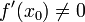. Além disso, para um zero de multiplicidade 1, a convergência é, pelo menos, quadrática (ver taxa de convergência) numa vizinhança do zero, o que significa que intuitivamente o número de dígitos correcção, pelo menos aproximadamente duplica em cada passo. Mais detalhes podem ser encontrados na seção de análise abaixo.

Exemplo

Considere o problema de encontrar o número positivo com x cos (x) = x ^3. Podemos reformular isso como encontrar o zero do f (x) = cos (x) - x ^3. Temos F '(x) = -sin (x) - 3 x ^2. Desde cos (x) ≤ 1 para todo x e x ^3> 1 para x> 1, sabemos que nosso zero, situa-se entre 0 e 1. Nós tentamos um valor inicial de x ₀ = 0,5.

Os dígitos corretos estão sublinhados no exemplo acima. Em particular, x ₆ é correcta para o número de casas decimais dadas. Nós vemos que o número de dígitos correcção depois dos aumentos de ponto decimais de 2 ₍₃ x) para a 5 e 10, que ilustra a convergência quadrática.

História

O método de Newton foi descrita por Isaac Newton em De analysi por Aequationes numero terminorum Infinitas (escrito em 1669, publicado em 1711 por William Jones) e em De metodis Fluxionum et serierum infinitarum (escrito em 1671, traduzido e publicado como Método de Fluxions em 1736 por John Colson). No entanto, sua descrição difere substancialmente da descrição moderna dada acima: Newton se aplica o método apenas para polinômios. Ele não computa as aproximações sucessivas 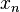, Mas calcula uma sequência de polinômios e só no final, ele chega a uma aproximação para a raiz x. Por fim, Newton vê o método como puramente algébrica e não consegue perceber a conexão com o cálculo. Isaac Newton provavelmente derivado seu método a partir de um método semelhante, mas menos precisos por François Viète. A essência do método de Viète pode ser encontrada no trabalho do persa matemático Sharaf al-Din al-Tusi (Ypma 1995). Um caso especial do método de Newton para calcular raízes quadradas era conhecido muito mais cedo e é frequentemente chamado de Método babilônico.

O método de Newton foi publicado pela primeira vez em 1685 em um tratado de álgebra tanto histórica e prática por John Wallis. Em 1690, Joseph Raphson publicou uma descrição simplificada em Universalis análise aequationum. Novamente Raphson viram o método de Newton puramente como um método algébrico e o seu uso restrito a polinómios, mas que descreve o método em termos das aproximações sucessivas x _n, em vez de a sequência mais complicada de polinómios usados por Newton. Finalmente, em 1740, Thomas Simpson descreveu o método de Newton como um método iterativo para resolver equações não-lineares gerais usando cálculo fluxional, essencialmente dando a descrição acima. Na mesma publicação, Simpson também dá a generalização para sistemas de duas equações e notas que o método de Newton podem ser utilizados para a resolução de problemas de optimização, definindo o gradiente a zero.

Arthur Cayley em 1879 em O problema imaginário Newton-Fourier foi o primeiro que percebeu as dificuldades em generalizar o método de Newton para as raízes complexas de polinômios com grau maior do que 2 e complexos valores iniciais. Isto abriu o caminho para o estudo da teoria de iterações de funções racionais.

Considerações práticas

Em geral, o convergência é quadrática: o erro é essencialmente quadrado em cada passo (isto é, o número de dígitos exactos duplica em cada passo). Há algumas ressalvas, no entanto. Em primeiro lugar, o método de Newton requer que o derivado ser calculados directamente. (Se o derivativo é aproximada pela declive de uma linha por meio de dois pontos da função, o secante resultados; isto pode ser mais eficiente, dependendo de como um medidas esforço computacional.) Em segundo lugar, se o valor inicial é demasiado longe do zero real, o método de Newton pode deixar de convergir. Devido a isso, as implementações mais práticos do método de Newton colocar um limite superior para o número de iterações e talvez do tamanho das itera. Em terceiro lugar, se o raiz sendo procurado tem multiplicidade maior que um, a taxa de convergência é meramente lineares (erros reduzidas por um factor constante em cada passo), a menos que sejam tomadas medidas especiais.

Uma vez que o mais grave dos problemas acima é a possibilidade de uma falha de convergência, Press et ai. (1992) apresentar uma versão do método de Newton, que começa no ponto médio de um intervalo em que a raiz é conhecido para deitar e pára a iteração se uma iteração é gerado, que se situa fora do intervalo.

Os desenvolvedores de sistemas informáticos de grande escala envolvendo constatação raiz tendem a preferir o método da secante sobre o método de Newton, porque a utilização de um quociente de diferença em lugar do derivado no método de Newton implica que o código adicional para calcular a derivada não necessita de ser mantido. Na prática, as vantagens de manter uma base de código menores geralmente superam as características de convergência superiores do método de Newton.

Exemplos contrários

As linhas tangentes da x ^ 3 - 2 x 2 + a 0 e 1 se cruzam o eixo x em 1 e 0, respectivamente, que ilustra o método de Newton por isso oscila entre estes valores para alguns pontos de partida.

Ponto de partida muito longe

Se o ponto de partida não está perto de uma raiz, em seguida, a convergência pode não ocorrer. Deixar

e tomar 0 como o ponto de partida. A primeira iteração produz 1 e a segunda iteração retorna a 0 até a seqüência irá oscilar entre os dois sem convergindo para uma raiz. Em geral, o comportamento da sequência pode ser muito complexa. (Ver Newton fractal.)

Nos exemplos seguintes, a raiz é desejado em zero para simplicidade-poderia ter sido colocado noutro local.

Derivada descontínua

Se o derivado não é contínua na raiz, em seguida, a convergência pode deixar de ocorrer em toda a vizinhança da raiz. Considere a função

Em seguida 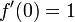e 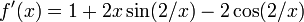noutro local.

Dentro de qualquer bairro da raiz, este derivado continua mudando sinal quando x tende a 0 da direita (ou à esquerda), enquanto 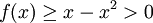para .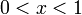

Assim 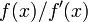é ilimitada perto da raiz e método de Newton não irá convergir, embora: a função é diferenciável em toda parte; o derivado não é zero na raiz; 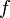é infinitamente diferenciável exceto na raiz; e o derivado é limitado em um bairro da raiz (ao contrário de seu recíproco).

No segundo derivado

Se não houver um segundo derivado na raiz, em seguida, a convergência pode deixar de ser quadrada. Com efeito, deixa

Em seguida

E

exceto quando 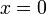onde é indefinido. Dado ,

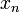que tem cerca de 4/3 vezes mais bits de precisão como 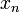tem. Isso é menos do que as duas vezes como muitos que seriam necessários para a convergência quadrática. Assim, a convergência do método de Newton (neste caso) não é quadrática, embora: a função é continuamente diferenciável em toda parte; o derivado não é zero na raiz; e 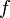é infinitamente diferenciável exceto na raiz desejado.

Zero derivado

Se a primeira derivada é zero na raiz, em seguida, a convergência não será quadrática. Com efeito, deixa

Em seguida 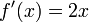e, consequentemente, 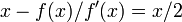. Assim, a convergência não é quadrática, mesmo que a função é infinitamente diferenciável em toda parte.

Análise

Suponha-se que a função f tem um zero em α, isto é, f (α) = 0.

Se f é continuamente diferenciável e seu derivado não desaparece em α, então existe um bairro de α tal que para todos os valores iniciais x ₀ naquele bairro, a seqüência {x _n} vontade convergem para α.

Se a função é diferenciável continuamente e o seu derivado não desaparece em α e que tem uma segunda derivada em α então a convergência é quadrática ou mais rápido. Se a segunda derivada não desaparece em α, em seguida, a convergência é meramente quadrática.

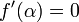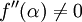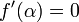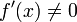Se o derivado não desaparecer a α, em seguida, a convergência é geralmente apenas linear. Especificamente, se f é duas vezes continuamente diferenciável, e , Então existe um bairro de α tal que para todos os valores iniciais x ₀ em que bairro, a seqüência de iteração converge linearmente, com log taxa de ₁₀ 2 (Suli e Mayers, Exercício 1.6). Alternativamente, se e noutro local, em um vizinhança U de α, α ser um zero de multiplicidade r e se 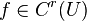então existe um bairro de α tal que para todos os valores iniciais x ₀ em que bairro, a seqüência de itera converge linearmente.

No entanto, mesmo convergência linear não é garantido em situações patológicas.

Na prática, estes resultados são locais e do bairro de convergência não são conhecidas a priori, mas há também alguns resultados de convergência global, por exemplo, dado um certo bairro de U ₊ α, se f é duas vezes diferenciável em U ₊ e se 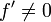, 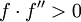em U _+, então, para cada x ₀ em U ₊ a sequência x _k é monotonamente decrescente para α.

Generalizações

Sistemas não-lineares de equações

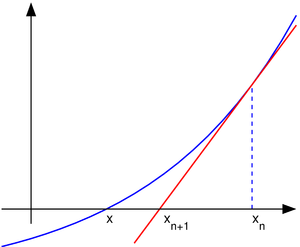
Pode-se usar o método de Newton também para resolver sistemas de k (não-lineares) equações, o que equivale a encontrar os zeros de funções continuamente diferenciável F: R → R ^{k k.} Na formulação dada acima, então deve-se à esquerda multiplicar com o inverso da k k -by- Jacobian matriz J _F (x _n) em vez de dividir por f '(x _n). Ao invés de realmente computar o inverso dessa matriz, pode-se economizar tempo, resolvendo o sistema de equações lineares

para o desconhecido x _{n + 1} - x _n. Mais uma vez, este método só funciona se o valor inicial x ₀ é perto o suficiente para o verdadeiro zero. Tipicamente, uma região que é bem comportado está localizado em primeiro lugar com algum outro método e o método de Newton é então utilizado para "polonês" uma raiz que já é conhecido aproximadamente.

Equações não-lineares em um espaço de Banach

Outra generalização é o método de Newton para encontrar um zero de uma função F definida em um Espaço de Banach. Neste caso, a formulação é

,

onde 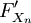é o Fréchet derivado aplicados no ponto 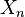. Uma das necessidades do derivado Fréchet a ser invertida em cada 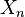para que o método seja aplicável.

Funções complexas

Bacias de atração para x ^5-1 = 0; mais escuro significa mais iterações para convergir.

Ao lidar com funções complexas, no entanto, o método de Newton pode ser aplicada directamente para encontrar os seus zeros. Para muitas funções complexas, o limite do jogo (também conhecido como o bacia de atração) de todos os valores iniciais que causam o método a convergir para um zero particular, é um fractal .