
Oeis
Informações de fundo
Esta seleção é feita para as escolas de caridade infantil leia mais . Clique aqui para mais informações sobre Crianças SOS.
A Enciclopédia On-Line de Integer Sequences (OEIS), também citou simplesmente como Sloane, é uma extensa pesquisável banco de dados de sequências de números inteiros, disponíveis gratuitamente na Web .
OEIS registra informações sobre sequências inteiras de interesse para ambos os profissionais matemáticos e amadores, e é amplamente citado. Ele contém mais de 135 mil sequências, tornando-se o maior banco de dados de seu tipo.
Cada entrada contém os principais termos da sequência, palavras-chave, motivações matemáticos, links literatura, e muito mais, incluindo a opção de gerar um gráfico ou um jogo representação musical da seqüência. O banco de dados é pesquisáveis por palavra-chave e por subsequência.
História
Neil Sloane começou a colecionar seqüências inteiras como um estudante em meados da década de 1960 para apoiar o seu trabalho na combinatória . O banco de dados foi armazenado a primeira em cartões perfurados. Ele publicou seleções do banco de dados em forma de livro duas vezes:
- A Handbook of Integer Sequences (1973, ISBN 0-12-648550-X), que contém 2400 sequências.
- A Enciclopédia das Sequências de Inteiros com Simon Plouffe (1995, ISBN 0-12-558630-2), contendo 5.487 seqüências.
Estes livros foram bem recebidos e, especialmente após a segunda publicação, os matemáticos fornecido Sloane com um fluxo constante de novas sequências. A coleção se tornou incontrolável em forma de livro, e quando o banco de dados tinham alcançado 16.000 entradas Sloane decidiu ir on-line pela primeira vez como um serviço de e-mail (agosto de 1994), e logo depois como um web site (1995). O banco de dados continua a crescer a uma taxa de cerca de 10.000 entradas por ano.
Sloane tem gerido pessoalmente 'seus' sequências há quase 40 anos, mas a partir de 2002, um conselho de editores associados e voluntários tem ajudado a manter o banco de dados.
Como um spin-off a partir do trabalho de banco de dados, Sloane fundou a Journal of Integer Sequências em 1998.
Em 2004, Sloane comemorou a adição da sequência de 100000 para o banco de dados, ![]() A100000. Em 2006, a interface do usuário foi reformada e foram adicionados mais recursos avançados de pesquisa.
A100000. Em 2006, a interface do usuário foi reformada e foram adicionados mais recursos avançados de pesquisa.
Não-inteiros
Além sequências inteiras estritamente falando, OEIS também catalogado sequências de frações , os dígitos de números transcendentes, números complexos e assim por diante, transformando-os em seqüências de números inteiros.
Sequências de números racionais são representados por duas sequências (nomeados com a palavra-chave 'frac'): a sequência de numeradores e a sequência de denominadores. Por exemplo, a quinta ordem Seqüência Farey, 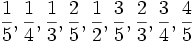 , Está catalogado como o numerador sequência de 1, 1, 1, 2, 1, 3, 2, 3, 4 (
, Está catalogado como o numerador sequência de 1, 1, 1, 2, 1, 3, 2, 3, 4 ( ![]() A006842) e o denominador sequência 5, 4, 3, 5, 2, 5, 3, 4, 5 (
A006842) e o denominador sequência 5, 4, 3, 5, 2, 5, 3, 4, 5 ( ![]() A006843).
A006843).
Números irracionais importantes, tais como π = 3,1415926535897 ... são catalogados sob sequências inteiras representativos tais como expansões decimais (aqui 3, 1, 4, 1, 5, 9, 2, 6, ... ( ![]() A000796)) ou expansões contínuas fracções (e aqui 3, 7, 15, 1, 292, 1, ... (
A000796)) ou expansões contínuas fracções (e aqui 3, 7, 15, 1, 292, 1, ... ( ![]() A001203)).
A001203)).
Convenções
O OEIS está actualmente limitada a planície ASCII texto, por isso usa uma forma linear de notação matemática convencional (como f (n) para as funções, n para as variáveis em execução, etc.). letras gregas são geralmente representados por seus nomes completos, por exemplo, , mu para μ, phi para φ.
Cada sequência é identificado pela letra A seguido de seis dígitos, por vezes, referida sem os zeros, por exemplo, A315, em vez de A000315.
Termos individuais sequências são separadas por vírgulas. Grupos de dígitos não são separados por vírgulas, pontos ou espaços.
Em comentários, fórmulas, etc., uma (n) representa o n th termo da seqüência.
Significado especial zero
Zero é muitas vezes usado para representar elementos de sequência não-existentes. Por exemplo, ![]() A104157 enumera a "menor privilegiada de n ² consecutivos primos para formar um n × n quadrado mágico de constante menos mágica, ou 0 se existe tal quadrado mágico existe. " O valor de um (1) (a quadrado mágico 1 × 1) é 2; um (3) é 1480028129. Mas não existe tal 2 × 2 quadrado mágico, portanto, um (2) é 0.
A104157 enumera a "menor privilegiada de n ² consecutivos primos para formar um n × n quadrado mágico de constante menos mágica, ou 0 se existe tal quadrado mágico existe. " O valor de um (1) (a quadrado mágico 1 × 1) é 2; um (3) é 1480028129. Mas não existe tal 2 × 2 quadrado mágico, portanto, um (2) é 0.
Esse uso especial tem uma base matemática sólida em determinadas funções de contagem. Por exemplo, a função totient de valência 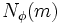 (
( ![]() A014197) conta as soluções de φ (x) = m. Há quatro soluções para 4, mas não há soluções para 14, portanto, um (14) de A014197 é 0-não existem soluções.
A014197) conta as soluções de φ (x) = m. Há quatro soluções para 4, mas não há soluções para 14, portanto, um (14) de A014197 é 0-não existem soluções.
Ocasionalmente -1 é usado para esta finalidade em vez disso, como em ![]() A072041.
A072041.
Ordenação lexicográfica
O OEIS mantém o ordem lexicográfica das sequências, de modo que cada sequência tem um predecessor e um sucessor (o seu "contexto"). OEIS normaliza as sequências de ordenação lexicographic, (normalmente) ignorando os zeros ou uns iniciais e também o sinal de cada elemento. Sequências de códigos de distribuição de peso, muitas vezes omitir zeros periodicamente recorrentes.
Por exemplo, considere: os principais números , os primes palindr�icas, a seqüência de Fibonacci , a sequência do fornecedor preguiçoso, e os coeficientes na expansão da série de 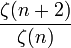 . Em OEIS ordem lexicográfica, são eles:
. Em OEIS ordem lexicográfica, são eles:
Sequência # 1: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...
Sequência # 2: 2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, ...
Sequência # 3: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
Sequência # 4: 1, 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, 67, 79, 92, ...
Sequência # 5: 1, -3, -8, -3, -24, 24, -48, -3, -8, 72, -120, 24, -168, 144, ...
Considerando que a ordenação lexicográfica unnormalized iria pedir essas seqüências assim: # 3, # 5, # 4, # 1, # 2.
A auto-referencialidade
Desde muito cedo na história da OEIS, muitas pessoas sugeriram sequências derivadas a partir da colocação de sequências no próprio OEIS. "Eu resisti adicionando estas sequências por um longo tempo, em parte por um desejo de manter a dignidade do banco de dados, e em parte porque A22 foi conhecida apenas para 11 termos!" Sloane relembrou.
Uma das seqüências mais antiga auto-referenciais Sloane aceito no OEIS foi ![]() A031135 (mais tarde
A031135 (mais tarde ![]() A091967) "um (n) = N-ésimo termo de sequência a_n". Esta sequência impulsionou o progresso em encontrar mais termos de
A091967) "um (n) = N-ésimo termo de sequência a_n". Esta sequência impulsionou o progresso em encontrar mais termos de ![]() A000022. Para maior n que correspondem a sequências que são finitos e dada na íntegra (as palavras-chave "fini" e "cheio"), um termo (n) de A091967 é indefinido.
A000022. Para maior n que correspondem a sequências que são finitos e dada na íntegra (as palavras-chave "fini" e "cheio"), um termo (n) de A091967 é indefinido.
![]() A100544 lista o primeiro mandato dado em seqüência A n, mas ele precisa ser atualizado de tempos em tempos por causa da mudança opiniões sobre compensações. Listagem em vez chamar um (1) de seqüência A n pode parecer uma boa alternativa se não fosse pelo fato de que algumas sequências de ter compensações de 2 e maior.
A100544 lista o primeiro mandato dado em seqüência A n, mas ele precisa ser atualizado de tempos em tempos por causa da mudança opiniões sobre compensações. Listagem em vez chamar um (1) de seqüência A n pode parecer uma boa alternativa se não fosse pelo fato de que algumas sequências de ter compensações de 2 e maior.
Esta linha de pensamento leva à pergunta "é n em seqüência A n?" e as sequências deliciosamente paradoxais ![]() A053873, n é em A n, e
A053873, n é em A n, e ![]() A053169, n não está em n. Assim, o número composto 2808 é em A053873 porque
A053169, n não está em n. Assim, o número composto 2808 é em A053873 porque ![]() A002808 é a sequência de números compostos, enquanto os não-prime 40 está em A053169, porque não é em A000040, os números primos. O paradoxo é que as sequências que 53.169 e 53.873 pertence? (Esta é uma forma de O paradoxo de Russell.)
A002808 é a sequência de números compostos, enquanto os não-prime 40 está em A053169, porque não é em A000040, os números primos. O paradoxo é que as sequências que 53.169 e 53.873 pertence? (Esta é uma forma de O paradoxo de Russell.)
Um exemplo resumida de uma entrada típica OEIS
Esta entrada, ![]() A046970, foi escolhido porque, com a excepção de um Programa de bordo, que contém todos os campos uma entrada OEIS pode ter.
A046970, foi escolhido porque, com a excepção de um Programa de bordo, que contém todos os campos uma entrada OEIS pode ter.
Número ID: A046970 URL: http://www.research.att.com/projects/OEIS?Anum=A046970 Sequência: 1,3,8,3,24,24,48,3,8,72,120,24,168,144,192,3,288 , 24,360,72, 384,360,528,24,24,504,8,144,840,576,960,3,960,864,1152,24, 1368,1080,1344,72,1680,1152,1848,360,192,1584,2208,24,48,72, 2304,504,2808 , 24,2880,144,2880,2520,3480,576 Assinado: 1, -3, -8, -3, -24,24, -48, -3, -8,72, -120,24, -168144192 , -3, -288, 24, -360,72,384,360, -528,24, -24.504, -8144, -840, -576, -960, -3, 960,864,1152,24, -1368,1080,1344, 72, -1680, -1152, -1848.360, 192,1584, -2208,24, -48,72,2304,504, -2808,24,2880,144,2880, 2520, -3480, -576 Nome : Criação de função Riemann Zeta: coeficientes na expansão da série de Zeta (n + 2) / Zeta (n). Comentários: ... Além de sinais também sum_ {d | n} núcleo (d) ^ 2 * mu (n / d), onde núcleo (x) é a parte squarefree de x. - Benoit Cloitre (abcloitre (AT) modulonet.fr), 31 de maio 2002 Referências M. Abramowitz e IA Stegun, Manual de funções matemáticas, Dover Publications, 1965, pp 805-811.. Links: função zeta Wikipedia, Riemann. Fórmula: multiplicativo com um (p ^ e) = 1-p ^ 2. um (n) = sum_ {d | n} mu (d) * d ^ 2. Exemplo: A (3) = -8, porque os divisores são de 3 {1, 3}, e Mu (1) * 1 ^ 2 + mu (3) * 3 ^ 2 = -8. A (4) = -3 porque os divisores são de 4 {1, 2, 4,}, e Mu (1) * 1 ^ 2 + Mu (2) * 2 ^ 2 + mu (4) * 4 ^ 2 = - 3 Math'ca: Mudd [d_]: = MoebiusMu [d] * d ^ 2; Tabela [Além disso@@Mudd [Divisores [n]], {n, 60}] (Lopez) Programa: (PARI) A046970 (n) = sumdiv (n, d, d ^ 2 * Moebius (d)) (Benoit Cloitre ) Veja também: Seqüência no contexto: A016623 A046543 A035292 A058936 A002017 A086179 this_sequence sequências adjacentes: A046967 A046968 A046969 A046971 A046972 A046973 this_sequence Cf. A027641 e A027642. Palavras-chave: sinal, mult Offset: 1 Autor (es): Douglas Stoll, dougstoll (AT) email.msn.com Extensão: Corrigida e prorrogado por Vladeta Jovovic (Vladeta (AT) Eunet.yu), 25 de julho de 2001 ... Campos de entrada
Número de identificação
Cada sequência no OEIS tem um número de série, um número inteiro positivo de seis dígitos, precedido A (e com zeros à esquerda, à esquerda antes de novembro de 2004). A letra "A" significa "absoluto". Números são atribuídos pelo editor (s) ou por um Distribuidor de número, o que é útil para quando contribuinte deseja enviar em sequências relacionadas de uma vez e ser capaz de criar referências cruzadas. Um número Um do dispensador expira um mês a partir de edição se não for usado. Mas, como a tabela de sequências arbitrariamente seleccionados na sequência de mostrar, a correspondência aproximada detém.
| A059097 | Números n tal que o coeficiente binomial C (2n, n) não é divisível pelo quadrado de um primo ímpar. | 01 de janeiro de 2001 |
| A060001 | Fibonacci (n) !. | 14 de março de 2001 |
| A066288 | Número de polyominoes 3-dimensional (ou polycubes) com n células e grupo de simetria de ordem exatamente 24. | 01 de janeiro de 2002 |
| A075000 | O menor número tal que n * A (n) é uma concatenação de n inteiros consecutivos ... | 31 de agosto de 2002 |
| A078470 | Fração continuou por Zeta (3/2) | 01 de janeiro de 2003 |
| A080000 | Número de permutações que satisfaçam -k <= p (i) -i <= r e P (i) -i | 10 de fevereiro de 2003 |
| A090000 | Duração do maior bloco contíguo de um de em expansão binária de primordial n-th. | 20 de novembro de 2003 |
| A091345 | Convolution exponencial do A069321 (n) com o próprio, onde montamos A069321 (0) = 0. | 01 de janeiro de 2004 |
| A100000 | Marcas do 22000-year-old osso Ishango do Congo. | 07 de novembro de 2004 |
| A102231 | Coluna 1 do triângulo A102230, e é igual à convolução de A032349 A032349 com deslocamento para a direita. | 01 de janeiro de 2005 |
| A110030 | Número de inteiros consecutivos começando com n necessário para somar a uma série Niven. | 08 de julho de 2005 |
| A112886 | Inteiros positivos livre de triângulo. | 12 de janeiro de 2006 |
| A120007 | Mobius transformar de soma de fatores primos de n | 02 de junho de 2006 |
Mesmo para as sequências no livro antecessores do OEIS, os números de identificação não são os mesmos. O 1973 Handbook of Integer Sequences continha cerca de 2.400 sequências, que foram numerados por ordem lexicográfica (a letra M e acrescido de 4 dígitos, com zeros à esquerda, se necessário), eo Encyclopedia of Integer Sequences 1995 continha 5.487 seqüências, também numerados pela ordem lexicográfica (o letra N, mais 4 dígitos, com zeros à esquerda, se necessário). Estes antigos números M e N, conforme aplicável, estão contidos no campo de número de ID entre parênteses após o moderno Um número.
URL
O campo URL dá o formato preferido para o URL para conectar-se a seqüência em questão, para simplificar recortar e colar.
Seqüência
O campo de sequência relaciona os próprios, ou no valor de pelo menos cerca de quatro linhas 'números. O campo de sequência não faz distinção entre sequências que são finitos, mas ainda muito tempo para exibir e sequências que são infinitas. Para ajudar a fazer essa determinação, você precisa olhar para o campo palavras-chave para "fini", "cheio", ou "mais". Para determinar a que n os valores indicados correspondem, ver o campo offset, que dá ao n para o primeiro mandato dado.
Quaisquer sinais negativos são removidos a partir deste campo, e os valores com sinais são colocados no campo Assinado.
Assinado
O campo assinada é quase a mesma coisa que o campo de sequência, exceto que ele mostra sinais negativos. Este campo só está incluído para sequências que têm valores negativos. Qualquer entrada com este campo deve ter a palavra-chave "sinal".
Nome
O campo de nome normalmente contém o nome mais comum para a sequência, e às vezes também a fórmula. Por exemplo, 1, 8, 27, 64, 125, 216, 343, 512, ( ![]() A000578) é nomeado "Os cubos: uma (n) = n ^ 3."
A000578) é nomeado "Os cubos: uma (n) = n ^ 3."
Comentários
O campo de comentários é para obter informações sobre a seqüência que não se encaixa em qualquer um dos outros campos. O campo de comentários muitas vezes aponta relações interessantes entre diferentes sequências e aplicações menos óbvias para uma seqüência. Por exemplo, Lekhraj sempre Beedassy em um comentário para A000578 observa que os números de cubo também contar o "número total de triângulos resultantes de entrecruzamento cevians dentro de um triângulo, de modo que dois dos seus lados são cada repartiu-N ", enquanto Sloane salienta a inesperada relação entre os números hexagonais centrados ( ![]() A003215) e segunda polinômios de Bessel (
A003215) e segunda polinômios de Bessel ( ![]() A001498) em um comentário para A003215.
A001498) em um comentário para A003215.
Se nenhum nome é dado para um comentário, o comentário foi feito pelo relator original da seqüência.
Maple, Mathematica, e outros programas
Maple e Mathematica são os programas preferidos para calcular sequências no OEIS, e ambos obter os seus próprios rótulos de campo, "bordo" e "Mathematica". Qualquer outro programa recebe um "Programa" rótulo de campo genérico e o nome do programa entre parênteses. O OEIS tem programas em PARI, Magma, Matlab, Python e até mesmo a Microsoft Excel.
Se não houver nenhum nome dado, o programa foi escrito pelo relator original da seqüência.
Palavras-chave
O OEIS tem seu próprio conjunto padrão de quatro ou cinco palavras-chave carta que caracterizam cada sequência:
- de base Os resultados do cálculo dependem de uma base posicionai específica. Por exemplo, 2, 3, 5, 7, 11, 101, 131, 151, 181 ...
 A002385 são números primos, independentemente de base, mas eles são palindromic especificamente na base 10. A maioria deles não são palindromic em binário. Algumas seqüências avaliaria esta palavra-chave, dependendo de como eles estão definidos. Por exemplo, 3, 7, 31, 127, 8191, 131071, ...
A002385 são números primos, independentemente de base, mas eles são palindromic especificamente na base 10. A maioria deles não são palindromic em binário. Algumas seqüências avaliaria esta palavra-chave, dependendo de como eles estão definidos. Por exemplo, 3, 7, 31, 127, 8191, 131071, ...  O A000668 não taxa "base" se definido como "primos da forma 2 ^ n - 1." No entanto, definidos como "primos repunit em binário", a sequência classificaria a palavra-chave "base".
O A000668 não taxa "base" se definido como "primos da forma 2 ^ n - 1." No entanto, definidos como "primos repunit em binário", a sequência classificaria a palavra-chave "base". - bref "seqüência é muito curta para fazer qualquer análise com", por exemplo,
 A079243, Número de classes de isomorfismo de anti-comutativos operações não anti-associativas não comutativos associativas fechadas binários em um conjunto de ordem n.
A079243, Número de classes de isomorfismo de anti-comutativos operações não anti-associativas não comutativos associativas fechadas binários em um conjunto de ordem n. - CoFR A sequência representa um fracção contínua.
- cons A seqüência é uma expansão decimal de uma importante constante matemática, como e ou π.
- Uma sequência de núcleo que é de importância fundamental para um ramo da matemática, tais como os números primos, a seqüência de Fibonacci, etc.
- mortos Esta palavra-chave utilizada para sequências erradas que têm aparecido em jornais ou livros, ou para cópias de seqüências existentes. Por exemplo,
 A088552 é o mesmo que A000668.
A088552 é o mesmo que A000668. - mudo Uma das palavras-chave mais subjetivas, por "sequências sem importância", que pode ou não se relacionam diretamente com a matemática.
 A001355, "Mix dígitos do pi e e." é um exemplo do primeiro caso, e
A001355, "Mix dígitos do pi e e." é um exemplo do primeiro caso, e  A082390, "Números sobre um teclado de computador, ler em uma espiral." é um exemplo do último.
A082390, "Números sobre um teclado de computador, ler em uma espiral." é um exemplo do último. - fácil Os termos da sequência pode ser facilmente calculado. Talvez a seqüência mais merecedor dessa palavra-chave é 1, 2, 3, 4, 5, 6, 7, ...
 A000027, onde cada termo é mais um do que o termo anterior. A palavra-chave "fácil" é dado às vezes a sequências de "primos da forma f (m)", onde f (m) é uma função facilmente calculado. (Embora, mesmo que F (m) é fácil de calcular para grande m, pode ser muito difícil determinar se f (m) é primo).
A000027, onde cada termo é mais um do que o termo anterior. A palavra-chave "fácil" é dado às vezes a sequências de "primos da forma f (m)", onde f (m) é uma função facilmente calculado. (Embora, mesmo que F (m) é fácil de calcular para grande m, pode ser muito difícil determinar se f (m) é primo). - eigen Uma seqüência de valores próprios .
- fini A sequência é finita, embora ainda pode conter mais termos do que pode ser exibido. Por exemplo, o campo de sequência de
 A105417 mostra apenas cerca de um quarto de todos os termos, mas um comentário observa que o último termo é 3888.
A105417 mostra apenas cerca de um quarto de todos os termos, mas um comentário observa que o último termo é 3888. - frac Uma seqüência de qualquer numeradores ou denominadores de uma sequência de frações que representam números racionais. Qualquer seqüência com esta palavra-chave deve ser uma referência cruzada com a sua sequência correspondente de numeradores ou denominadores, embora isso pode ser dispensado para seqüências de Fracções egípcias, como
 A069257, onde a sequência de numerador seria
A069257, onde a sequência de numerador seria  A000012. Esta palavra-chave não deve ser utilizado para sequências de fracções contínuas, CoFR deve ser usada para esse fim, em vez.
A000012. Esta palavra-chave não deve ser utilizado para sequências de fracções contínuas, CoFR deve ser usada para esse fim, em vez. - O pleno campo de sequência mostra a sequência completa. Se uma seqüência tem a palavra-chave "cheio", ele também deve ter o "fini". Palavra-chave Um exemplo de uma sequência finita dada na totalidade é o do primes supersingular
 A002267, dos quais há precisamente quinze.
A002267, dos quais há precisamente quinze. - duro Os termos da sequência não pode ser facilmente calculado, mesmo com número bruto de energia esmaga. Esta palavra-chave é mais frequentemente usado para sequências correspondentes a problemas não resolvidos, como "Como muitas esferas pode tocar uma outra esfera do mesmo tamanho?"
 A001116 lista as dez primeiras soluções conhecidas.
A001116 lista as dez primeiras soluções conhecidas. - menos A "seqüência menos interessante".
- Os próximos mais termos da sequência não são conhecidos.
- mult A sequência corresponde a um função multiplicativa. Prazo um (1) deve ser 1, e um prazo (mn) pode ser calculado multiplicando a (m) por um (n) se m e n são primos entre si. Por exemplo, em
 A046970, um (12) = A (3) A (4) = -8 × -3.
A046970, um (12) = A (3) A (4) = -8 × -3. - novo Para sequências que foram adicionados no último par de semanas, ou tiveram uma grande extensão recentemente. Esta palavra-chave não é dada uma caixa de seleção no formulário Web para a apresentação de novas sequências, o programa da Sloane acrescenta que, por padrão, quando aplicável.
- agradável Talvez a palavra-chave mais subjetiva de tudo, de "sequências excepcionalmente agradáveis."
- Nonn A seqüência consiste em inteiros não negativos (que podem incluir zeros). Não é feita qualquer distinção entre as sequências que consistem de números não negativos só porque dos escolhidos compensados (por exemplo, n 3, os cubos, que são todos positivos de n = 0 para a frente) e aqueles que, por definição, são completamente não-negativo (por exemplo, n 2, os quadrados).
- OBSC A sequência é considerada obscura e precisa de uma definição melhor. Uma sequência com esta palavra-chave,
 A025046 foi olhado por pelo menos um outro OEIS colaborador que era incapaz de reproduzir os resultados fornecidos pelo relator original.
A025046 foi olhado por pelo menos um outro OEIS colaborador que era incapaz de reproduzir os resultados fornecidos pelo relator original. - probation sequências que "podem ser excluídos mais tarde, a critério do editor."
- assinar alguns (ou todos) dos valores da sequência são negativos. A entrada inclui tanto um campo Assinado com os sinais e um campo de seqüência que consiste em todos os valores passados pelo valor absoluto da função.
- tabf "Um irregular (ou em forma engraçado-) matriz de números feitos em uma seqüência de lê-lo linha por linha." Por exemplo,
 A071031, "Triângulo lido por linhas que dão sucessivos estados de autômato celular gerada pela" regra 62. "
A071031, "Triângulo lido por linhas que dão sucessivos estados de autômato celular gerada pela" regra 62. " - Tabl Uma sequência obtida através da leitura de um arranjo geométrico de números, tal como um triângulo ou quadrado, linha por linha. O exemplo por excelência é o triângulo de Pascal lido por linhas,
 A007318.
A007318. - UNED Sloane não editou a sequência, mas acredita que poderia valer a pena incluindo na OEIS. A seqüência pode conter erros de cálculo ou tipográfico. Contribuintes são convidados a refletir sobre a seqüência e enviar Sloane sua edição.
- unkn "Pouco se sabe" sobre a seqüência, nem mesmo a fórmula que produz. Por exemplo,
 A072036, que foi apresentado a um oráculo Internet para ponderar.
A072036, que foi apresentado a um oráculo Internet para ponderar. - andar "Counts anda (ou caminhos auto-evitando)."
- palavra Depende das palavras de um idioma específico. Por exemplo, zero, um, dois, três, quatro, cinco, etc, 4, 3, 3, 5, 4, 4, 3, 5, 5, 4, 3, 6, 6, 8, 8, 7, 7, 9, 8, 8 ...
 A005589, "Número de letras no nome Inglês de N, excluindo os espaços e hífens."
A005589, "Número de letras no nome Inglês de N, excluindo os espaços e hífens."
Algumas palavras-chave são mutuamente excludentes, a saber: núcleo e mudo, fácil e difícil, cheio e mais, menos e agradável, e Nonn e assinar.
Compensar
O deslocamento é o índice do primeiro mandato dado. Para algumas sequências, o deslocamento é óbvio. Por exemplo, se a lista a sequência de números de quadrados como 0, 1, 4, 9, 16, 25 ..., o deslocamento é 0; enquanto se listá-la como 1, 4, 9, 16, 25 ..., o deslocamento é 1. O desvio padrão é 0, ea maioria das sequências no OEIS ter compensado de 0 ou 1. Sequência ![]() A073502, a constante mágica para n × n quadrado mágico com entradas principais (de 1 como um prime) com somas menores de linha, é um exemplo de uma seqüência com deslocamento 3, e
A073502, a constante mágica para n × n quadrado mágico com entradas principais (de 1 como um prime) com somas menores de linha, é um exemplo de uma seqüência com deslocamento 3, e ![]() A072171, "Número de estrelas de magnitude visual n." é um exemplo de uma sequência com offset -1.
A072171, "Número de estrelas de magnitude visual n." é um exemplo de uma sequência com offset -1.
Às vezes pode haver discordância sobre o que os termos iniciais da sequência são, e, correspondentemente, o que o deslocamento deve ser. No caso de o sequência do fornecedor preguiçoso, o número máximo de peças que você pode cortar uma panqueca em com n cortes, o OEIS dá a seqüência como 1, 2, 4, 7, 11, 16, 22, 29, 37, ... ![]() A000124, com offset 0, enquanto Mathworld dá a sequência de 2, 4, 7, 11, 16, 22, 29, 37, ... (implícita compensar 1). Pode-se argumentar que não fazer cortes para a panqueca é tecnicamente um número de cortes, ou seja, n = 0. Mas pode também ser argumentado que uma panqueca sem cortes é irrelevante para o problema.
A000124, com offset 0, enquanto Mathworld dá a sequência de 2, 4, 7, 11, 16, 22, 29, 37, ... (implícita compensar 1). Pode-se argumentar que não fazer cortes para a panqueca é tecnicamente um número de cortes, ou seja, n = 0. Mas pode também ser argumentado que uma panqueca sem cortes é irrelevante para o problema.
Embora o deslocamento é um campo obrigatório, alguns participantes não se preocupam em verificar se o deslocamento de 0 padrão é apropriado para a sequência em que estão enviando.
O formato interno, na verdade, mostra dois números para o deslocamento. O primeiro é o número acima descrito, enquanto que o segundo representa o índice da primeira entrada (contando a partir de 1), que tem um valor absoluto maior que 1. O segundo valor é usado para acelerar o processo de busca de uma sequência. Assim ![]() A000001, que começa a 1, 1, 1, 2 com a primeira entrada que representa um (1) tem 1, 4 como o valor interno do campo de deslocamento.
A000001, que começa a 1, 1, 1, 2 com a primeira entrada que representa um (1) tem 1, 4 como o valor interno do campo de deslocamento.
Autor (s)
O autor da sequência é a pessoa que apresentou a sequência, mesmo que a sequência é conhecida desde os tempos antigos. O nome do remetente é dada primeiro nome (escrito por extenso), inicial do meio (s) (se aplicável) e último nome; esta em contraste com a forma como os nomes estão escritos nos campos de referência. O e-mail do remetente também é dado, com o caráter @ substituída por "(AT)". Para a maioria das sequências após A055000, o campo autor também inclui a data em que o apresentador enviado na seqüência. Mas quando o apresentador é um dos colaboradores mais freqüentes no campo autor acaba de iniciais; "njas" para si mesmo Neil Sloane, por exemplo.
Pesquisando na OEIS
A versão anterior da página look-up principal do OEIS ofereceu três maneiras de olhar-se sequências, e o botão de opção direita teve de ser selecionado. Houve uma página look-up avançado, mas a sua utilidade foi integrado a página look-up principal em uma grande reformulação da interface em janeiro de 2006.
Digite uma seqüência
Digite alguns termos da sequência, separadas por espaços ou vírgulas (ou ambos).
Você pode inserir sinais negativos, mas eles serão ignorados. Por exemplo, 0, 3, 7, 13, 20, 28, 36, 43, 47, 45, 32, 0, -64, n 2 menos o n-ésimo número de Fibonacci, é uma sequência que não é tecnicamente no OEIS, mas o muito semelhante seqüência 0, -3, -7, -13, -20, -28, -36, -43, -47, -45, -32, 0, 64, está no OEIS e vai vir para cima quando uma procura por seu homólogo sinais invertidos.
No entanto, a pesquisa pode ser forçado para combinar sinais usando o "sinal:" prefixo na string de pesquisa. Isto é especialmente útil para a sequências como ![]() A008836 que é exclusivamente composto por aqueles positivos e negativos.
A008836 que é exclusivamente composto por aqueles positivos e negativos.
Um pode entrar tão pouco como um único inteiro ou até quatro linhas de termos. Sloane recomenda entrar seis termos, a (2) para um (7), a fim de obter resultados suficientes, mas não muitos resultados. Há casos em que entrar apenas um número inteiro dá precisamente um resultado, como 1990661 traz apenas ![]() A007597, a primes strobogrammatic). E há também casos em que se pode entrar muitos termos e ainda não restringir os resultados para baixo tudo o que muito.
A007597, a primes strobogrammatic). E há também casos em que se pode entrar muitos termos e ainda não restringir os resultados para baixo tudo o que muito.
Digite uma palavra
Digite uma seqüência de caracteres alfanuméricos. Determinados caracteres, como letras acentuadas estrangeiros, não são permitidos. Assim, para procurar sequências respeitantes aos O problema de znam, tente inseri-lo sem os acentos: ". O problema de Znam" A manipulação de apóstrofos foi bastante melhorado no redesenho de 2006. As seqüências de pesquisa " triângulo de Pascal "," Pascals triângulo "e" triângulo de Pascal "todos dão os resultados desejados.
Para pesquisar mais números poligonais por palavra, tente "números n-gonal" em vez de "números de prefixo-gonal gregas" (por exemplo, "os números de 47 Gonal" em vez de "números heptaquartagonal"). Beyond " dodecagonal números ", palavra que procuraram com os prefixos gregos pode deixar de produzir os resultados desejados.
Introduza um número de seqüência
Digite o OEIS moderno Um número da seqüência, com a letra A e com ou sem preenchimento de zero. A partir de 2006, os antigos números de seqüência M e N irá produzir o resultado adequado, como seqüências de pesquisa, por exemplo, uma pesquisa por M0422 vai abrir corretamente ![]() A006047, o número de entradas no n º linha do triângulo de Pascal não é divisível por 3 (M0422 no livro A Enciclopédia das Integer Sequências) e não
A006047, o número de entradas no n º linha do triângulo de Pascal não é divisível por 3 (M0422 no livro A Enciclopédia das Integer Sequências) e não ![]() A000422, concatenação de números de n para baixo a 1.
A000422, concatenação de números de n para baixo a 1.
Pesquisando a partir de um navegador da Web
Um OpenSearch compatível navegador (como Firefox 2.0 ou Internet Explorer 7) pode ter OEIS adicionado à sua lista de pesquisa da barra de ferramentas com base adicionando um provedor com a seguinte URL: http://www.research.att.com/~njas/sequences/?q=TEST&language=english Pode-se então entrar directamente na sequência, por exemplo, "1,2,6,24,120" (sem aspas) na barra de pesquisa e procurar OEIS facilmente.

