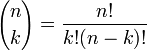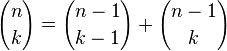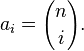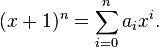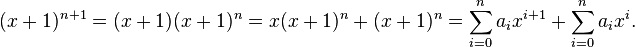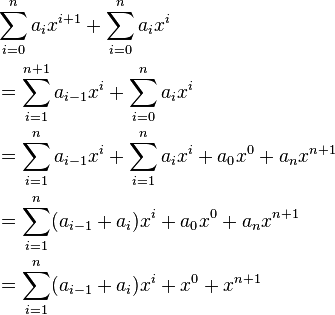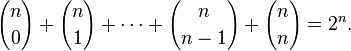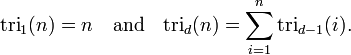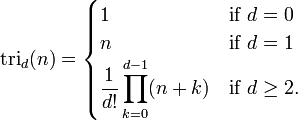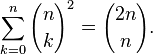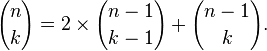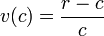Triângulo de Pascal

Assuntos Relacionados: Matemática

Você sabia ...

Crianças SOS feita esta seleção Wikipedia ao lado de outras escolas recursos . Um link rápido para o patrocínio criança é http://www.sponsor-a-child.org.uk/

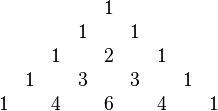
$\ Begin {matrix} &&&&& 1 \\ &&&& 1 && 1 \\ &&& 1 && && 2 1 \\ 1 && && && 3 3 1 && \\ & 1 && && 4 6 4 && && 1 \ end {matrix}$

As primeiras cinco fileiras de triângulo de Pascal

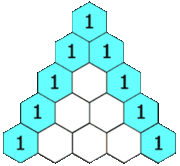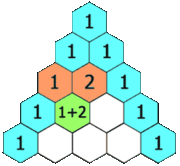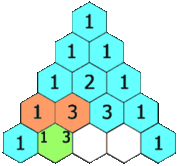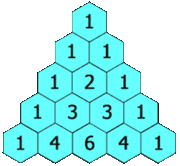
Em matemática , triângulo de Pascal é um arranjo geométrico dos coeficientes binomial em um triângulo . É nomeado após Blaise Pascal em grande parte do mundo ocidental, embora outros matemáticos estudou séculos antes dele na Índia , Pérsia , China e Itália . As linhas de triângulo de Pascal são convencionalmente enumerados começando com linha zero, e os números de linhas ímpares são geralmente desfasadas uma em relação aos números de filas. Uma construção simples do triângulo procede da seguinte forma. Na linha zeroth, escrever apenas o número 1. Em seguida, para construir os elementos de seguintes linhas, adicione o número diretamente acima e para a esquerda com o número diretamente acima e à direita para encontrar o novo valor. Se tanto o número para a direita ou esquerda não está presente, substituir um zero em seu lugar. Por exemplo, o primeiro número na primeira fila é 0 + 1 = 1, enquanto que os números 1 e 3 da terceira fila são adicionados para produzir o número 4 na quarta linha.

Cada número no triângulo representa a soma dos dois, directamente por cima.

Esta construção está relacionada com os coeficientes binomial pela Regra de Pascal, que afirma que se

${N \ escolher k} = \ frac {n!} {K! (N-k)!}$

é o k-ésimo coeficiente binomial no expansão binomial de (x + y) ^n, em que n! é o fatorial de n, em seguida,

${N \ escolher k} = {n-1 \ escolher k-1} + {n-1 \ escolher k}$

para qualquer número inteiro não negativo n e k qualquer número inteiro entre 0 e n.

Triângulo de Pascal tem maior generalizações dimensional. A versão tridimensional é chamado A pirâmide de Pascal ou tetraedro de Pascal, enquanto as versões gerais são chamados Simplices de Pascal - veja também pirâmide , tetraedro , e simplex.

O triângulo

Abaixo estão as linhas de zero a dezesseis do triângulo de Pascal:

                                                 1
                                              1 1
                                           1 2 1
                                        1 3 1 3
                                     1 4 6 1 4
                                  1 5 10 10 1 5
                               1 6 15 20 15 6 1
                            1 7 21 35 35 21 7 1
                         1 8 28 56 70 56 28 8 1
                      1 9 36 84 126 126 84 36 9 1
                   1 10 45 120 210 252 210 120 45 10 1
                1 11 55 165 330 462 462 330 165 55 11 1
             1 12 66 220 495 792 924 792 495 220 66 12 1
          1 13 78 286 715 1287 1716 1716 1287 715 286 78 1 13
       1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
    1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
 1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1

Triângulo e binômio expansões de Pascal

Triângulo de Pascal determina os coeficientes que surgem em expansões binomial. Por exemplo, considere a expansão

(X + y) = ² x ² + 2 + y xy ² = 1 x ^{2 0} + 2 Y ¹ Y ¹ x 1 + ⁰ x y ^2.

Notam os coeficientes são os números de linha de dois triângulo de Pascal: 1, 2, 1. Em geral, quando um binomial como x + y é elevado a uma potência inteiro positivo, temos:

(X + y) ⁿ = ₀ um x ⁿ + ₁ um ^{n -1} x + y ₂ x ^{N -2} y ² + ... + _n uma _-1 xy ^{n -1} + a _n y ^n,

onde os coeficientes a _i nesta expansão são precisamente os números em linha n do triângulo de Pascal. Em outras palavras,

$a_i = {n \ i} escolher.$

Isto é o teorema binomial.

Observe que todo direita diagonal de triângulo de Pascal corresponde ao coeficiente de y ⁿ nestas expansões binomial, enquanto os próximos diagonais corresponde ao coeficiente de xy ^{n -1} e assim por diante.

Para ver como o teorema binomial refere-se a uma construção simples do triângulo de Pascal, considerar o problema do cálculo dos coeficientes de expansão de (x + 1) ^n-1 em termos dos coeficientes correspondentes de (x + 1) ⁿ (y configuração = 1 para simplificar). Suponhamos que então

$(X + 1) ^ n = \ sum_ {i = 0} ^ n a_i x ^ i.$

Agora

$(X + 1) ^ {n + 1} = (x + 1) (x + 1) ^ n x = (x + 1) ^ n + (x + 1) ^ N = \ sum_ {i = 0} ^ n a_i x ^ {i + 1} + \ sum_ {i = 0} ^ n a_i x ^ i.$

Os dois somatórios podem ser reorganizados como segue:

$\ Begin {align} & \ sum_ {i = 0} ^ {n} a_ {i} x ^ {i + 1} + \ sum_ {i = 0} ^ n a_i x ^ i \\ & {} = \ sum_ {i = 1} ^ {n + 1} a_ {i-1} x ^ {i} + \ sum_ {i = 0} ^ n a_i x ^ i \\ & {} = \ sum_ {i = 1} ^ {n} a_ {i-1} x ^ {i} + \ sum_ {i = 1} ^ n a_i x ^ i + 0 + a_0x ^ a_ {n} x ^ {n + 1} \\ & {} = \ sum_ {i = 1} ^ {n} (a_ {i-1} + a_i) x ^ {i} + 0 + a_0x ^ a_ {n} x ^ {n + 1} \\ & {} = \ sum_ {i = 1} ^ {n} (a_ {i-1} + a_i) x ^ {i} + x ^ 0 + x ^ {n + 1} \ end {align}$

(Por causa de como levantar um polinômio para uma obra de poder, um ₀ = a _n = 1).

Agora temos uma expressão para o polinômio (x + 1) ^{n +1} em termos dos coeficientes de (x + 1) ⁿ (estes são os a _i s), que é o que precisamos, se queremos expressar uma linha em termos da linha acima. Lembre-se que todos os termos em uma diagonal que vai do canto superior esquerdo para o canto inferior direito correspondem à mesma potência de x, e que os a-termos são os coeficientes do polinômio (x + 1) ^n, e nós estamos determinando os coeficientes de (x + 1) ^n-1. Agora, para qualquer dado que não 0 ou N + 1, o coeficiente do termo x ⁱ no polinomial (x + 1) ⁿ é igual a ¹ um _i (a figura de cima e para a esquerda da figura, a determinar , uma vez que é na mesma diagonal) + a _{i-1 (figura} à direita imediata da primeira figura). Esta é certamente a regra simples para a construção de triângulo linha por linha de Pascal.

Não é difícil transformar esse argumento em uma prova (por indução matemática) do teorema binomial.

Uma consequência interessante do teorema binário é obtido ajustando ambas as variáveis x e y igual a um. Neste caso, sabemos que 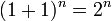$(1 + 1) = ^ n 2 ^ n$ , Então

${N \ escolher 0} + {n \ escolher 1} + \ cdots + {n \ escolher n-1} + {n \ n} = escolher 2 ^ n.$

Em outras palavras, a soma das entradas na n-ésima linha de triângulo de Pascal é o enésimo potência de dois.

Padrões e propriedades

Triângulo de Pascal tem muitas propriedades e contém muitos padrões de números.

As diagonais

Alguns padrões simples são imediatamente aparentes nas diagonais do triângulo de Pascal:

As diagonais indo ao longo das bordas esquerda e direita conter apenas a 1.
As diagonais ao lado das diagonais ponta conter os números naturais em ordem.
Movendo-se para dentro, o par seguinte de diagonais conter o números triangulares em ordem.
O próximo par de diagonais conter o números tetraédricos em ordem e dar o próximo par números pentatope. Em geral, cada par seguinte de diagonais contém o seguinte "d dimensional superior - "números simplex, que podem ser definidos como

$\ Textrm {} _1 tri (n) = n \ quad \ mbox {e} \ quad \ textrm {tri} _ {} d (n) = \ sum_ {i = 1} ^ n \ mathrm {tri} _ {d -1} (i).$

Uma alternativa fórmula é a seguinte:

$\ Textrm {} _d tri (n) = \ begin {cases} 1 & \ mbox {if} d = 0 \\ n & \ mbox {if} d = 1 \\ \ displaystyle \ frac {1} {d!} \ Prod_ {k = 0} ^ {d-1} (n + k) & \ mbox {if} d \ ge 2. \ end {cases}$

O significado geométrico de uma função tri _d é: _d tri (1) = 1 para todas as d. Construir uma d - dimensional triângulo (um triângulo 3-dimensional é um tetraedro ) colocando pontos adicionais abaixo de um ponto inicial, o que corresponde a tri _d (1) = 1. Colocar estes pontos de uma maneira análoga à colocação de números em triângulo de Pascal. Para encontrar tri _d (x), temos um total de x pontos que compõem a forma de destino. tri _d (X), em seguida, é igual ao número total de pontos em forma. Um triângulo 1-dimensional é simplesmente uma linha e, portanto, _uma tri (x) = x, que representa a sequência de números naturais. O número de pontos em cada camada corresponde a tri _{d - 1} (x).

Triângulo de Sierpinski

Outros padrões e propriedades

O padrão obtido pela coloração apenas os números ímpares no triângulo de Pascal se assemelha ao fractal chamado Triângulo de Sierpinski, e essa semelhança torna-se cada vez mais preciso quanto mais linhas são consideradas; no limite, como o número de linhas se aproxima do infinito, o padrão resultante é o triângulo Sierpinsky. De modo mais geral, os números poderiam ser colorido diferente consoante são ou não múltiplos de 3, 4, etc .; isto resulta em outros padrões e combinações.

Imagine que cada número do triângulo é um nó numa grelha que se encontra ligado aos números adjacentes acima e abaixo dele. Agora, para qualquer nó no grid, contar o número de caminhos lá na grade (sem recuo) que ligam este nó para o nó superior (1) do triângulo. A resposta é o número Pascal associada a esse nó. A interpretação do número em triângulo de Pascal como o número de caminhos para esse número a partir da ponta significa que numa Tabuleiro de jogo Plinko forma de um triângulo, a probabilidade de ganhar prêmios mais próximas do centro será maior do que ganhar prêmios nas bordas.

O valor de cada linha, se cada número é considerado como uma casa decimal e números maiores do que 9 são transportados em consequência, é uma potência de 11 (especificamente, 11 ^n, onde n é o número da linha). Por exemplo, linha dois lê '1, 2, 1', que é 11 ² (121). Na fileira cinco, '1, 5, 10, 10, 5, 1' é traduzido para 161.051 depois de levar os valores sobre, que é de 11 ^5. Esta propriedade é facilmente explicado pela configuração x = 10 na expansão binomial de (x + 1) ^{número de linha,} e ajustando os valores para caber no sistema de numeração decimal.

Padrões mais sutis

Há também, padrões sutis mais surpreendentes. A partir de um único elemento do triângulo, uma linha diagonal mais superficial pode ser formada por um elemento de movimento contínuo para a direita, em seguida, um elemento para o canto inferior direito, ou indo na direcção oposta. Um exemplo é a linha com os elementos 1, 6, 5, 1, que se inicia a partir da linha 1, 3, 3, 1 e termina três linhas para baixo. Tal "diagonal" tem uma soma que é um número de Fibonacci . No caso do exemplo, o número de Fibonacci é 13:

                                        1
                                     1 1
                                  1 2 1
                               1 → ↓ 3 3 1
                            1 4 → 6 → 4 ↓ 1
                         1 5 10 10 → 5 → 1 ↓
                      1 → ↓ 6 15 20 15 6 1 →
                    1 7 → 21 35 35 21 7 1
                 1 8 28 56 70 56 28 8 1
               1 9 36 84 126 126 84 36 9 1
             1 10 45 120 210 252 210 120 45 10 1
           1 11 55 165 330 462 462 330 165 55 11 1
         1 12 66 220 495 792 924 792 495 220 66 12 1
       1 13 78 286 715 1287 1716 1716 1287 715 286 78 1 13
     1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1 
   1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
 1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1

O segundo destaque diagonal tem uma soma de 233. Os números "pulado" entre o direito movimento eo movimento para baixo-direita também somar os números de Fibonacci, sendo os números »entre« os montantes formados pela primeira construção. Por exemplo, os números pulados na primeira diagonal em destaque são 3, 4 e 1, tornando-8.

Além disso, se linha m é tomado para indicar fileira 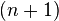$(N + 1)$ , A soma dos quadrados dos elementos de linha elemento de símbolo m é igual a meio da fileira 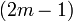$(2m-1)$ . Por exemplo, 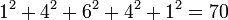$1 ^ 2 + 4 ^ 2 + 6 ^ 2 + 4 ^ 2 + 1 ^ 2 = 70$ . Em forma geral:

$\ Sum_ {k = 0} ^ n {n \ escolher k ^ 2} = {2n \ escolher n}.$

Outro padrão interessante é que em qualquer linha m, onde m é ímpar, o termo médio prazo menos os dois pontos para a esquerda é igual a um Número catalão, especificamente a (m + 1) / 2 número catalão. Por exemplo: na linha 5, 6 - 1 = 5, que é o ^3º número catalão, e (5 + 1) / 2 = 3.

Além disso, a soma dos elementos da fileira m é igual a 2 ^{m -1.} Por exemplo, a soma dos elementos da linha 5 está 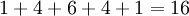$1 + 4 + 6 + 4 + 1 = 16$ , O que é igual a 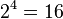$2 ^ 4 = 16$ . Isso decorre do teorema binominal provado acima, aplicada a (1 + 1) ^{m -1.}

Alguns dos números em triângulo de Pascal correlacionam-se com números em Triângulo de Lozanić.

Outra propriedade interessante do triângulo de Pascal é que, em linhas onde o segundo número (o primeiro número seguinte 1) é primo, todos os termos em que linha, exceto os 1s são múltiplos de que prime.

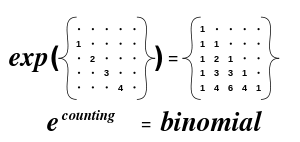
Binomial como matriz exponencial de matriz (Ilustração por 5 × 5 matrizes). Todos os pontos representam 0.

A matriz exponencial

Devido à sua construção simples por factoriais, uma representação muito básico de triângulo de Pascal em termos de matriz exponencial pode ser dado: o triângulo de Pascal é o exponencial da matriz que tem a sequência 1, 2, 3, 4, ... em seu subdiagonal e zero em qualquer outro lugar.

Propriedades geométricas

Triângulo de Pascal pode ser utilizado como um tabela de referência para o número de elementos dimensionados arbitrariamente dentro de uma única versão arbitrariamente dimensionada de um triângulo (conhecido como um simplex). Por exemplo, considere a 3a linha do triângulo, com valores de 1, 3, 3, 1. Um triângulo 2-dimensional tem um elemento 2-dimensional (si), três elementos 1-dimensionais (linhas, ou arestas), e três elementos 0 tridimensionais ( vértices, ou cantos). O significado do número final (1) é mais difícil de explicar (mas ver abaixo). Continuando com nosso exemplo, um tetraedro tem um elemento 3-dimensional (em si), quatro elementos tridimensionais (2 faces), seis elementos 1-dimensionais (arestas), e quatro elementos 0 tridimensionais (vértices). Adicionando o final de 1 de novo, estes valores correspondem à quarta linha do triângulo (1, 4, 6, 4, 1). A linha 1 corresponde a um ponto, e a linha 2 corresponde a um segmento de linha (dupla). Este padrão continua a arbitrariamente altos-hiper-dimensionado tetraedros (simplices).

Para entender por que este padrão existe, é preciso primeiro entender que o processo de construção de uma -simplex n de um (n - 1) -simplex consiste em simplesmente adicionando um novo vértice a este último, posicionada de tal modo que este novo vértice se encontra fora do espaço do simplex original, e conectá-lo a todos os vértices originais. Como exemplo, considere o caso da construção de um tetraedro de um triângulo, o último dos cujos elementos são enumerados por linha 3 do triângulo de Pascal: um rosto, três arestas e três vértices (o significado da final 1 será explicado em breve) . Para construir um tetraedro de um triângulo, que posicionar um novo vértice acima do plano do triângulo e ligar este vértice para todos os três vértices do triângulo original.

O número de um dado elemento tridimensional no tetraedro é agora a soma de dois números: em primeiro lugar que o número de elemento encontrado no triângulo original, mais o número de novos elementos, cada um dos quais é construído sobre elementos de uma dimensão de menos do triângulo original. Assim, no tetraedro, o número de células poliédricas (elementos) é 0 (o triângulo original não possui nenhuma) + 1 (construída sobre a face única do triângulo original) = 1; o número de faces é 1 (o próprio triângulo original) + 3 (as novas caras, cada um construído sobre uma aresta do triângulo original) = 4; o número de arestas é 3 (a partir do triângulo original) + 3 (as novas arestas, cada um construído em cima de um vértice do triângulo original) = 6; o número de novos vértices 3 é (a partir do triângulo original) + 1 (o novo vértice que foi adicionada para criar o tetraedro do triângulo) = 4. Este processo de soma do número de elementos de uma determinada dimensão para aqueles com menos uma dimensão para chegar ao número do primeiro encontrada no próximo simplex superior é equivalente ao processo de soma de dois números adjacentes numa fila de triângulo de Pascal, para se obter o número abaixo. Deste modo, o significado do número final (1) numa linha de triângulo de Pascal fica entendido como representando o novo vértice que é para ser adicionado à simplex representado por essa linha para produzir a próxima maior simplex representado pela linha seguinte. Este novo vértice está associado a cada elemento na simplex original para produzir um novo elemento de uma dimensão maior na nova simplex, e esta é a origem do padrão verificou-se ser idêntico ao observado em triângulo de Pascal.

Um padrão similar é observado relativa a praças , em oposição aos triângulos. Para encontrar o padrão, deve-se construir um analógico para o triângulo de Pascal, cujas entradas são os coeficientes de (x + 2) ^{Número Row,} em vez de (x + 1) ^{Número Row.} Existem algumas maneiras de fazer isso. O mais simples é começar com Row 0 = 1 e Linha 1 = 1, 2. Prossiga para construir os triângulos analógicos de acordo com a seguinte regra:

${N \ escolher k} = 2 \ times {n-1 \ escolher k-1} + {n-1 \ escolher k}.$

Isto é, escolher um par de números de acordo com as regras do triângulo de Pascal, mas o dobro do outro à esquerda antes de acrescentar. Isto resulta em:

                              1
                          1 2
                      1 4 4
                  1 6 12 8
              1 8 24 32 16
          1 10 40 80 80 32
      1 12 60 160 240 192 64
  1 14 84 280 560 672 448 128

A outra maneira de fabricação deste triângulo é começar com o triângulo de Pascal e multiplicar cada entrada por 2 ^k, onde k é a posição na linha do número dado. Por exemplo, o segundo valor na linha 4 do triângulo de Pascal é 6 (a inclinação da 1s corresponde à entrada de ordem zero em cada linha). Para obter o valor que reside na posição correspondente no triângulo analógico, multiplicar por 2 ^Posição 6 ^N = 6 × 2 × ² = 6 4 = 24. Agora que o triângulo analógico tenha sido construído, o número de elementos de qualquer dimensão que compor um arbitrariamente dimensionadas cubo (chamado hipercubo) pode ser lido a partir da tabela de uma forma análoga ao triângulo de Pascal. Por exemplo, o número de elementos 2-dimensional em um cubo de 2 dimensões (um quadrado) é um, o número de elementos (1-dimensionais lados, ou linhas) é de 4, e o número de elementos 0-dimensionais (pontos, ou vértices) é 4. Isto corresponde à segunda linha da tabela (1, 4, 4). Um cubo tem um cubo, 6 faces, 12 arestas, e oito vértices, que corresponde à linha seguinte do triângulo analógico (1, 6, 12, 8). Este padrão continua indefinidamente.

Para compreender porque este padrão existe, primeiro reconhecer que a construção de um n de uma -cube (n - 1) -cube é feito simplesmente por duplicação do número original e deslocando-a alguma distância (para um n -cube regular, o comprimento da aresta ) ortogonal ao espaço da figura original, em seguida, ligando cada vértice do novo valor para o seu vértice correspondente do original. Este processo de duplicação inicial é a razão pela qual, para enumerar os elementos tridimensionais de um n -cube, deve-se dobrar o primeiro de um par de números consecutivos deste análogo de triângulo de Pascal soma antes, para se obter o número abaixo. A duplicação inicial produz, assim, o número de elementos de "original" pode ser encontrada no seguinte mais elevado n -cube e, como antes, os novos elementos são construídos, os dos menos uma dimensão (bordas em cima vértices, enfrenta sobre arestas, etc.). Mais uma vez, o último número de uma linha representa o número de novos vértices para ser adicionado para gerar o próximo mais elevado n -cube.

Neste triângulo, a soma dos elementos da fileira m é igual a 3 ^{m - 1} Novamente, a utilização de elementos de fileira 5, como um exemplo.: 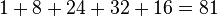$1 + 8 + 24 + 32 + 16 = 81$ , O que é igual a $3 ^ 4 = 81$ .

Yang Hui triângulo (de Pascal), como representado pelos chineses usando numerais haste.

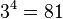Calculando uma linha individual

Este algoritmo é uma alternativa ao método de cálculo padrão células individuais com factoriais. Começando no lado esquerdo, o valor do primeiro célula é 1. Para cada célula após, o valor é calculado multiplicando o valor para a esquerda por uma fracção mudando lentamente:

$v (c) = \ frac {} r-C {c}$

Onde r = + 1 linha, começando com 0, na parte superior, e c = coluna, começando com 0, à esquerda. Por exemplo, para calcular a linha 5, R 6 =. O primeiro valor é 1. O próximo valor é 1 x 5/1 = 5. Os valores de redução do numerador por um, eo denominador aumenta em um a cada passo. Então, 5 x 4/2 = 10. Em seguida, 10 x 3/3 = 10. Em seguida, 10 x 2/4 = 5. Em seguida, 5 x 1/5 = 1. Observe que a última célula é sempre igual a 1, a multiplicação final está incluída para a integralidade da série.

Um padrão similar existe em um descendente diagonal. Começando com o primeiro e o número natural na cela ao lado, formam uma fração. Para determinar a próxima célula, aumentar o numerador eo denominador de cada por um, e, em seguida, multiplicar o resultado anterior pela fração. Por exemplo, a linha de partida com 1 e 7 formam uma fracção de 7/1. A próxima célula é 7 x 8/2 = 28. A próxima célula é de 28 x 9/3 = 84.

Note-se que para qualquer linha individual você só precisa calcular metade (arredondado para cima) o número de valores na linha. Isto é porque a linha é simétrica.

História

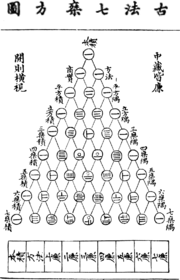
As primeiras representações explícitas de um triângulo de coeficientes binomial ocorrer no século 10 em comentários sobre a Chandas Shastra, um livro indiana antiga em sânscrito prosódia escrito por Pingalá entre o 5th- 2 BC séculos. Enquanto o trabalho de Pingala só sobrevive em fragmentos, o comentarista Halayudha, em torno 975, utilizado no triângulo para explicar referências obscuras para Meru-prastaara, o "Escadaria da Mount Meru ". Ele também se percebeu que as diagonais rasas da soma triângulo para os números de Fibonacci . O matemático indiano Bhattotpala (c. 1068) mais tarde dá linhas 0-16 do triângulo.

Por volta da mesma época, foi discutido na Pérsia ( Irã ) pela matemático Al-Karaji (953-1029) e do poeta - astrônomo e matemático Omar Khayyam (1048-1131); assim, o triângulo é referido como o "Khayyám triângulo" em Irão . Vários teoremas relacionados com o triângulo eram conhecidos, incluindo o teorema binomial. Na verdade, podemos ter bastante certeza que Khayyam utilizado um método de encontrar n º raízes baseadas na expansão binomial, e, portanto, sobre os coeficientes binomial.

No século 13, Yang Hui (1238-1298) apresentou o triângulo aritmético, que era o mesmo que o triângulo de Pascal . Hoje o triângulo de Pascal é chamado " Triângulo de Yang Hui "na China .

Finalmente, na Itália , ele é conhecido como "triângulo de Tartaglia", nomeado para o algebraist italiano Niccolò Fontana Tartaglia, que viveu um século antes Pascal (1500-1577); Tartaglia é creditado com a fórmula geral para resolver polinômios cúbicos (que pode ser realmente a partir de Scipione del Ferro, mas foi publicado pela Gerolamo Cardano 1545).

Petrus Apianus (1495 -1552) publicou o triângulo no frontispício de seu livro sobre cálculos de negócios 1531-1532 e uma versão anterior em 1527 o primeiro registro dele na Europa.

Em 1655, Blaise Pascal escreveu um triângulo arithmétique Traité du (Treatise on triângulo aritmético), em que ele colecionou diversos resultados então conhecidos sobre o triângulo, e empregou-los para resolver problemas na teoria da probabilidade . O triângulo foi mais tarde nomeado após Pascal por Pierre Raymond de Montmort (1708) e Abraham de Moivre (1730).

Retirado de " http://en.wikipedia.org/w/index.php?title=Pascal%27s_triangle&oldid=208833303 "

We provide Linux to the World